算法工具箱之前缀和

前缀和

概念：前缀和（Prefix Sum）是一种重要的预处理技术，能够在O(1)时间内快速计算数组任意区间的和。

核心思想：对于数组nums，我们预先计算一个前缀和数组prefix，其中：

prefix[i]表示nums[0]到nums[i]的和

一维前缀和：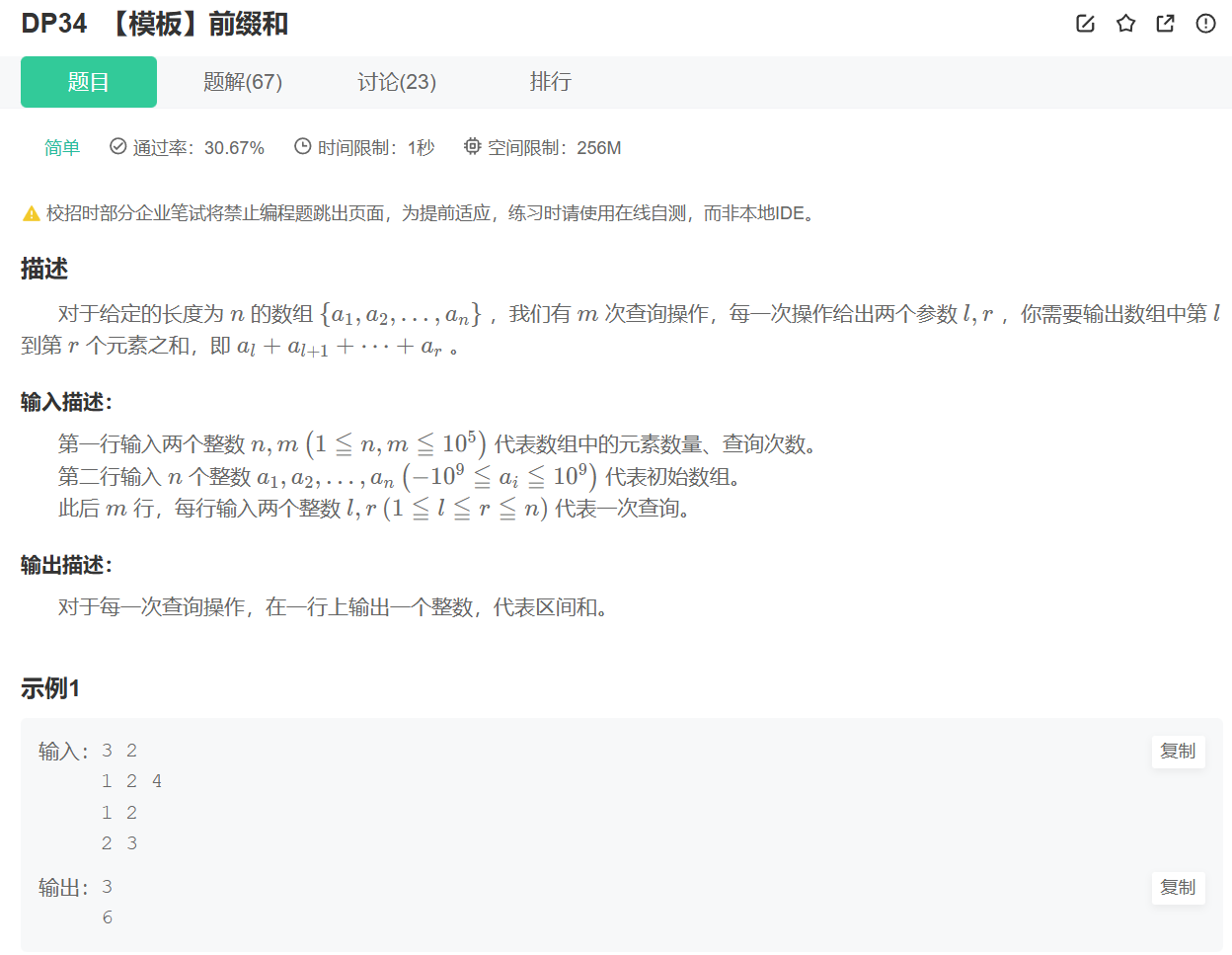

#include<iostream>
#include<vector>
using namespace std;
int main()
{long long n,m;cin>>n>>m;vector<long long> arr1(n);vector<long long> arr2(n + 1);arr2[0] = 0;for(auto &x : arr1){scanf("%d",&x);}for(int j = 1;j < arr2.size();j++){arr2[j] = arr2[j-1] + arr1[j-1];}long long l,r;for(int i = 0;i < m;i++){cin>>l>>r;cout<<arr2[r] - arr2[l - 1]<<endl;}return 0;
}

算法思路：先构建一个比原数组长度+1的前缀和数组，再将arr2[0] =0；然后⽤ arr2[i] 表⽰： [1, i] 区间内所有元素的和，那么 arr2[i - 1] ⾥⾯存的就是 i - 1 区间内所有元素的和，那么：可得递推公式：arr2[i] = arr2[i - 1] + arr1[i]。使⽤前缀和数组，「快速」求出「某⼀个区间内」所有元素的和：当询问的区间是[l, r] 时：区间内所有元素的和为：arr2[r] - arr2[l - 1]。

算法优势：

（1）查询高效：将O(n)的区间求和优化为O(1)的差值计算

（2）预处理思想：一次构建，多次使用

（3）扩展性强：可扩展到二维、多维情况

二位前缀和：

#include<iostream>
#include<vector>
using namespace std;
int main() {int m, n, q;cin >> m >> n >> q;vector<vector<int>> arr(m, vector<int>(n));vector<vector<long long>> arr2(m + 1, vector<long long>(n + 1));for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {cin >> arr[i][j];}}vector<vector<int>> arr1(q, vector<int>(4));for (int x = 0; x < q; x++) {for (int i = 0; i < 4; i++) {cin >> arr1[x][i];}}for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {arr2[i][j] = arr2[i - 1][j] + arr2[i][j - 1] + arr[i - 1][j - 1] - arr2[i - 1][j- 1];}}for (int i = 0; i < q; i++) {int x1 = arr1[i][0], y1 = arr1[i][1], x2 = arr1[i][2], y2 = arr1[i][3];cout << arr2[x2][y2] - arr2[x1 - 1][y2] - arr2[x2][y1 - 1] + arr2[x1 - 1][y1 -1] << endl;}return 0;
}

算法思路：类⽐于⼀维数组的形式，如果我们能处理出来从 元素的累加和，就可以在 [0, 0] 位置到 [i, j] 位置这⽚区域内所有 O(1) 的时间内，搞定矩阵内任意区域内所有元素的累加和。

（1）搞出来前缀和矩阵：这⾥就要⽤到⼀维数组⾥⾯的拓展知识，我们要在矩阵的最上⾯和最左边添加上⼀⾏和⼀列 0，这样我们就可以省去⾮常多的边界条件的处理。我们填写前缀和矩阵数组的时候，下标直接从 1 开始，能⼤胆使⽤ i - 1 , j - 1 位 置的值。

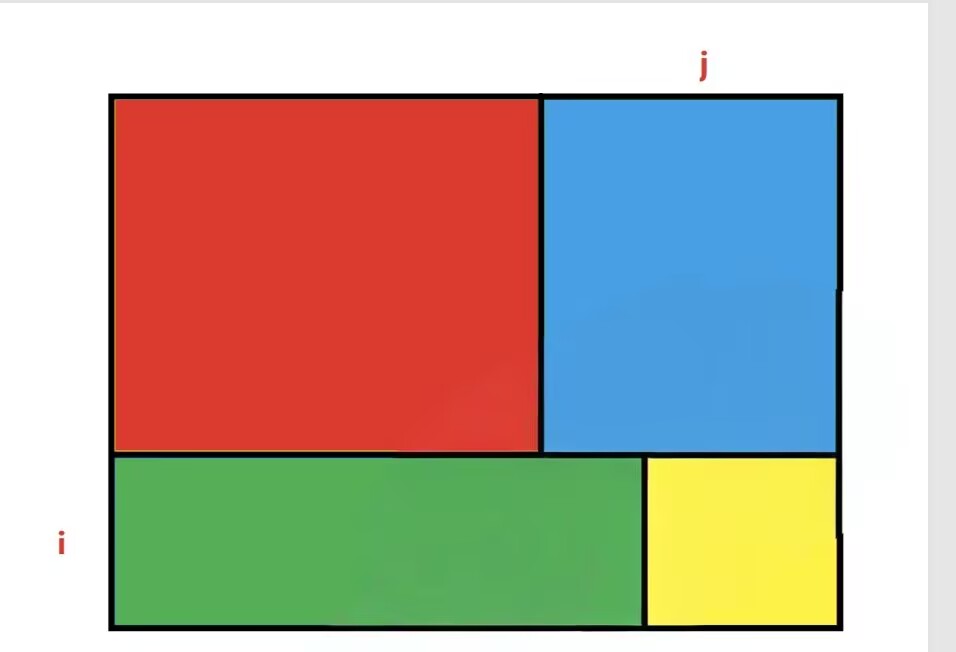
递归方程就是s[i][j]=s[i−1][j]+s[i][j−1]−s[i−1][j−1]+a[i][j]

黄= 新格子 a[i][j]

红+蓝= s[i-1][j]（上一行到 j 列的和）

红+绿= s[i][j-1]（这一行到 j-1 列的和）

红= s[i-1][j-1]（上一行 j-1 列的和）

所以红+蓝+红+绿=红+蓝+绿+红（红多算了一次），因此s[i][j]=(红+蓝)+(红+绿)−红+黄。

（2）查询公式（求子矩阵和）

查询 (x1,y1)到 (x2,y2)的和：sum=s[x2][y2]−s[x1−1][y2]−s[x2][y1−1]+s[x1−1][y1−1]

用颜色划分理解：把整个大矩形 s[x2][y2]分成四个区域：

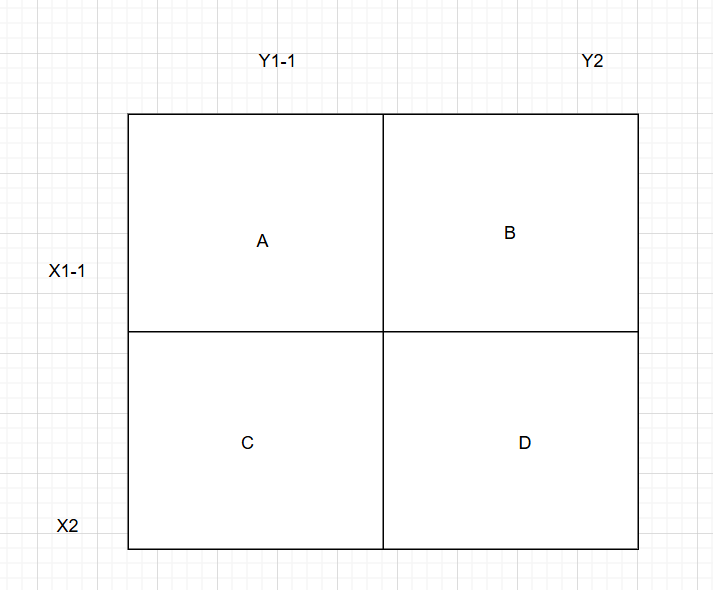
D= 我们要查询的子矩阵 (x1,y1)到 (x2,y2)，A+B+C+D= s[x2][y2]，A+B= s[x1-1][y2],A+C= s[x2][y1-1],A= s[x1-1][y1-1]。

所以D=(A+B+C+D)−(A+B)−(A+C)+A即D=s[x2][y2]−s[x1−1][y2]−s[x2][y1−1]+s[x1−1][y1−1]。

后缀和：

概念：从一个元素开始，到数组末尾的所有元素之和。

具体来说，给定一个数组 nums，它的后缀和数组 suffixSum是另一个数组，其中每个元素 suffixSum[i]的定义如下：suffixSum[i] = nums[i] + nums[i+1] + ... + nums[n-1]。这里，n是数组 nums的长度。

计算后缀和的步骤：从后往前遍历。（与前缀和思想类似）

例题：

class Solution
{
public:int pivotIndex(vector<int>& nums){int ret = -1;vector<int> arr1(nums.size(), 0);vector<int> arr2(nums.size(), 0);int x = arr1.size() - 1;for (int i = 1; i < nums.size(); i++){arr1[i] = arr1[i - 1] + nums[i - 1];}for (int i = x-1; i >= 0; i--){arr2[i] = arr2[i+1] + nums[i + 1];}for (int i = 0; i < nums.size(); i++){if (arr1[i] == arr2[i]){return i;}}return ret;}
};

核心思路：

我们要寻找一个下标 i，使得：左侧和 = 右侧和

所以我们发现只要前缀和和后缀和相等，那么这个中心下标就是这个i。