当前位置： 首页 > news >正文

C++ map和set的实现和封装

news 2025/11/5 10:40:20

map和set都是基于红黑树去实现的。

1. 红黑树的完善

1.1 看看库

在使用map和set函数时，我们通常认为set只需要一个K，map需要一个键值对K,V，来实现操作，但是在库里面并不是这样子的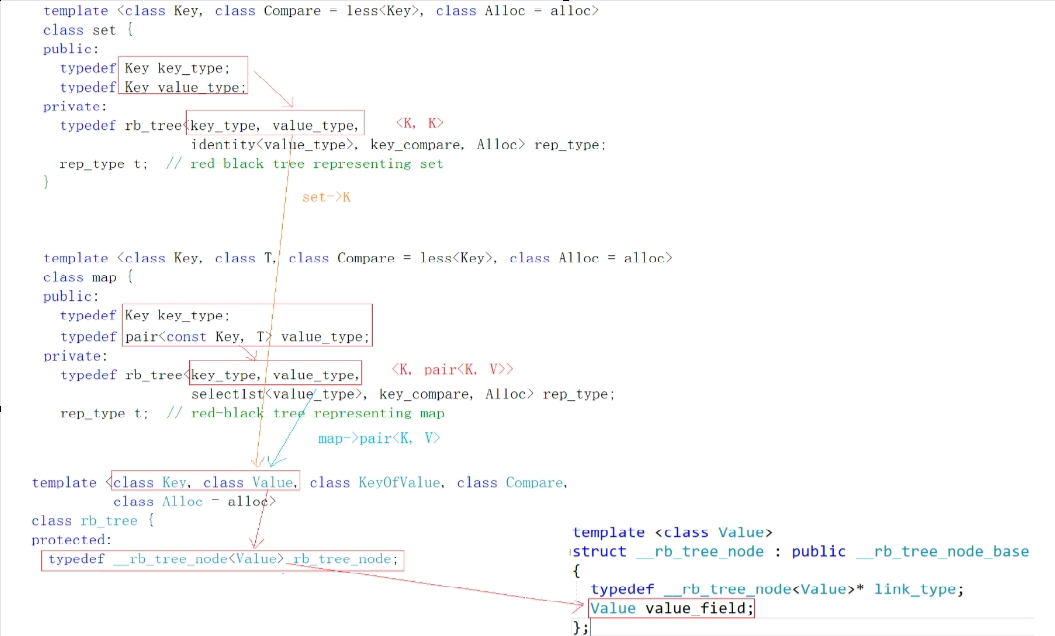

库里面的底层是set也是一个键值对<K,K>模型，map则是<K.pair<K,V>>,这样子的实现也是为了更好的实现查找和删除的操作，对于map而言，查找和删除需要传入K值，所以就需要把K给提取出来，set为了适配红黑树的前两个参数，所以设置了两个K值，set迁就了map。

ps：set和map表示两棵树，是一棵树的不同模板。

1.2 仿函数的设计

底层的红黑树中，在进行插入的操作是，set传过来的是K，而map传过来的pair<K,V>，在内部比较大小的时候可以设计仿函数来控制set就通过K来比较，map传过来的pair<K,V>,但是通过K来比较。

struct SetofT
{const K& operator()(const K& key)//怎么链接起来的{return key;}
};
struct MapofT
{const K& operator()(const pair<K, V>& kv){return kv.first;}
};

1.3 节点的构造

enum color
{RED,BLACK
};
template<class T>
struct RBTreeNode
{RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;color _col;T _data;RBTreeNode(const T&data): _left(nullptr), _right(nullptr), _parent(nullptr),_data(data), _col(RED){}
};

对于map的k，v和set的k，把_data类型设置为模板来匹配map和set，如果是set就实例化为k，map就为pair<k,v>。

1.4 迭代器的实现

1.4.1 构造

_Treeiterator(Node* node):_node(node)
{}
Node* _node;
_Treeiterator(const iterator&it):_node(it._node)
{}

这里提供了两种构造方法，重点是第二种，看上去是用迭代器来构造迭代器，如果是普通迭代器的话就是拷贝构造，如果是const迭代器的话就是构造，支持普通迭代器转化为const迭代器，这边是为了支持后面set的insert问题(后面就说到)。

1.4.2 operator*()

n当对正向迭代器进行解引用操作时，我们直接返回 对应结点数据的引用

Ref operator*()
{return _node->_data;
}

1.4.3 operator->()

当对正向迭代器进行->操作时，我们直接返回对应结点数据的指针

	Ptr operator->(){return &_node->_data;}

1.4.4 operator!=/==()

operator重载!= 和 ==，比较时直接比较Node*即可（地址最容易比较是否相等）

bool operator!=(const self& s)
{return _node != s._node;
}
bool operator==(const self& s)
{return _node == s._node;
}

1.4.5 operator++()

self& operator++()
{if (_node->_right){Node* subleft = _node->_right;while (subleft->_left){subleft = subleft->_left;}_node = subleft;}else{Node* cur = _node;Node* parent = cur->_parent;while (parent&&cur == parent->_right){cur = cur->_parent;parent = parent->_parent;}_node = parent;}return *this;
}

如果当前节点的右子树不为空的话，就去找右子树的最左节点。

如果当前节点的右子树为空的的话，就找下一个访问的孩子节点是父亲左的那一个父亲节点。

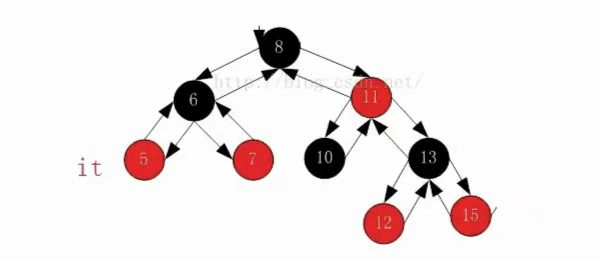
以6节点为例子，在向上的路径中，8号节点的左指向6号节点，所以++应该指向8号节点，如果是15号节点，就会一直向上寻找，cur节点指向8号节点，parent节点为8号的父节点，也就为空，就返回空。

1.4.6 operator--()

self& operator--()
{if (_node->_left){Node* subright = _node->_left;while (subright->_right){subright = subright->_right;}_node = subright;}else{Node* cur = _node;Node* parent = cur->_parent;while (parent&&cur == parent->_left){cur = cur->_parent;parent = parent->_parent;}_node = parent;}return *this;
}

如果当前节点的左子树不为空的话，就去找右子树的最右节点。

如果当前节点的左子树为空的的话，就找下一个访问的孩子节点是父亲右的那一个父亲节点。

1.4.7 迭代器完整代码

template<class T,class Ptr,class Ref>
struct _Treeiterator//节点的指针
{typedef RBTreeNode<T> Node;typedef _Treeiterator<T,Ptr,Ref> self;typedef _Treeiterator<T, T*, T&> iterator;_Treeiterator(Node* node):_node(node){}Node* _node;_Treeiterator(const iterator&it):_node(it._node){}Ref operator*(){return _node->_data;}Ptr operator->(){return &_node->_data;}bool operator!=(const self& s){return _node != s._node;}bool operator==(const self& s){return _node == s._node;}self& operator--(){if (_node->_left){Node* subright = _node->_left;while (subright->_right){subright = subright->_right;}_node = subright;}else{Node* cur = _node;Node* parent = cur->_parent;while (parent&&cur == parent->_left){cur = cur->_parent;parent = parent->_parent;}_node = parent;}return *this;}self& operator++(){if (_node->_right){Node* subleft = _node->_right;while (subleft->_left){subleft = subleft->_left;}_node = subleft;}else{Node* cur = _node;Node* parent = cur->_parent;while (parent&&cur == parent->_right){cur = cur->_parent;parent = parent->_parent;}_node = parent;}return *this;}
};

1.5 红黑树的接口实现

要实现接口的实现，就需要迭代器和节点对象，所以定义节点对象和迭代器的对象。

typedef RBTreeNode<T> Node;
typedef _Treeiterator<T,T*,T&> iterator;
typedef _Treeiterator<T, const T*, const T&> const_iterator;

1.5.1 begin和end函数

iterator begin()
{Node* leftmin = _root;while (leftmin && leftmin->_left){leftmin = leftmin->_left;}return iterator(leftmin);
}
iterator end()
{return iterator(nullptr);
}
const_iterator begin()const
{Node* leftmin = _root;while (leftmin && leftmin->_left){leftmin = leftmin->_left;}return const_iterator(leftmin);
}
const_iterator end()const
{return const_iterator(nullptr);
}

begin也就是根节点的左子树的最左节点，end直接设为空。

1.5.1 find函数

Node* find(const T& data)
{Node* cur = _root;KeyofT kot;while (cur){if (kot(cur->_data) < data){cur = cur->_right;}else if (kot(cur->_data) > data){cur = cur->_left;}else{return cur;}}return nullptr;
}

返回节点的指针，这里就需要用到仿函数来实现不同的类模板处理不同的类型，查找成功，返回插入节点的指针，失败返回空。

1.5.2 insert函数

	pair<iterator,bool> insert(const T& data){KeyofT kot;if (_root == nullptr){_root = new Node(data);_root->_col = BLACK;return make_pair(iterator(_root),true);}Node* parent = nullptr;Node* cur = _root;while (cur){if (kot(cur->_data)<kot(data)){parent = cur;cur = cur->_right;}else if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else{return make_pair(iterator(cur), false);}}cur = new Node(data);cur->_col = RED;if (kot(parent->_data) < kot(data)){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED)//uncle存在且为红{parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;//继续向上处理cur = grandfather;parent = cur->_parent;}else{//uncle不存在或者为黑if (cur == parent->_left){rootright(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{rootleft(parent);rootright(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED)//uncle存在且为红{uncle->_col = BLACK;parent->_col = BLACK;grandfather->_col = RED;//继续向上调整cur = grandfather;parent = cur->_parent;}else{//uncle不存在或者为黑if (cur == parent->_right){rootleft(grandfather);grandfather->_col = RED;parent->_col = BLACK;}else{rootright(parent);rootleft(grandfather);grandfather->_col = RED;cur->_col = BLACK;}break;}}}_root->_col = BLACK;return make_pair(iterator(cur), true);}

这里的insert步骤在红黑树右说过，做出的改变就是使用模板来分别处理set和map。

2.红黑树的封装

2.1 set的封装

#pragma once
#include"RBTree.h"
namespace bit
{template<class K>class set{struct SetofT{const K& operator()(const K& key){return key;}};public:typedef typename RBTree<K, K, SetofT>::const_iterator iterator;typedef typename RBTree<K, K, SetofT>::const_iterator const_iterator;const_iterator begin()const{return _t.begin();}const_iterator end()const{return _t.end();}pair<iterator,bool> insert(const K& key){pair<typename RBTree<K, K, SetofT>::iterator, bool> ret = _t.insert(key);//此时的_t的迭代器为普通迭代器，而需要接受的应该是const迭代器，所以需要将普通//迭代器构造成const迭代器。return pair<iterator, bool>(ret.first, ret.second);}private:RBTree<K, K, SetofT> _t;};
}

这边对于迭代器的使用把普通的迭代器和const的迭代器都设置为const的迭代器，set的K值是不可以修改的，所以迭代器都应该为cosnt迭代器，但是这边会有一个新的问题，我们把普通迭代器爷定为const迭代器，但是insert函数的返回值中的迭代器是普通迭代器啊，类型不匹配，所以我们在迭代器的定义时需要支持普通迭代器转化为const迭代器。

ps：这边的typename是告诉编译器我是一个类型，不是对象什么的，可以定义对象。

2.2 map的封装

#include"RBTree.h"
namespace bit
{template<class K,class V>class map{struct MapofT{const K& operator()(const pair<K, V>& kv){return kv.first;}};public:typedef typename RBTree<K, pair<const K, V>, MapofT>::iterator iterator;typedef typename RBTree<K, pair<const K, V>, MapofT>::const_iterator const_iterator;iterator begin(){return _t.begin();}iterator end(){return _t.end();}const_iterator begin()const{return _t.begin();}const_iterator end()const{return _t.end();}V& operator[](const K& key){pair<iterator, bool> ret = _t.insert(make_pair(key, V()));//没有就插入，有就提取return ret.first->second;}pair<iterator,bool> insert(const pair<K, V>& kv){return _t.insert(kv);}private:RBTree<K, pair<const K, V>, MapofT> _t;};
}

对于map来说，const的迭代器要保证k，v都不能被修改，但是如果像set那样子去设置的话，明显是不可能的，map支持键值对中的v可以被修改，所以在初始化时，直接把v定义为const，保证不能被修改。

ps：这边的typename是告诉编译器我是一个类型，不是对象什么的，可以定义对象。

http://www.dtcms.com/a/569716.html

相关文章：

  • 免费个人主页网站品牌设计公司50强
  • visual studio C# 如果只提供某个自建dll的命名空间，但是不添加引用，编译会通过吗
  • 手机手机网站制作应用商店软件大全
  • Maya导出abc文件到ue附带材质属性（中文版）
  • 数智管理学（五十五）
  • Oracle HugePages到底该怎么配置？
  • 河源市seo网站设计抖音带运营团队有用吗
  • 2025年11月4日 AI快讯
  • SAP定价过程
  • ArrayList常见面试题二
  • 网站建设中期报告织梦网站怎么做索引地图
  • 关键字匹配高效算法
  • PySide6 Win10记事本从零到一——第八章 查看菜单界面与功能实现
  • Linux之arm SMMUv3 驱动重要宏和函数解析（11）
  • 网站功能介绍是什么自贡网站设计
  • 做企业网站设wordpress多媒体权限
  • CTF WEB入门 命令执行篇 50-70
  • 利用网上菜谱做网站公众号开发公司排行榜
  • 免费搭建视频网站硬件开发板
  • Mysql中页分裂、合并的问题
  • Qt 的 QSqlDatabase 不能跨线程复用
  • Qt-QtCharts
  • 某番切小说畅听红果等提示“低版本不安全”的解决方案
  • 昆明网站seo技术厂家网站设计远程培训
  • Linux基本架构
  • 任务调度框架：PowerJob、XXL-Job、OpenJob
  • 做模型挣钱的网站wordpress中英文切换
  • TensorFlow Keras
  • 萧山做网站的企业wordpress集成关注公众和登陆
  • 详解EtherNet/IP转CAN边缘计算网关：基恩士PLC与CAN IO卡通讯配置步骤