自动驾驶运动规划 | 基于自行车模型的运动学模型和横向动力学模型详细推导图解
目录
- 1 运动学 vs 动力学
- 2 车辆运动学推导
- 3 车辆横向动力学推导
- 4 车辆横向动力学的误差形式
1 运动学 vs 动力学
机器人运动学主要研究机器人运动的几何特性而不考虑产生运动的力和力矩,它从几何角度描述机器人的位置、姿态、速度和加速度等运动关系;机器人动力学则进一步研究引起机器人运动的力和力矩之间的关系,分析控制力矩与产生的运动之间的映射规律,二者共同构成了机器人建模、轨迹规划与运动控制的理论基础。
自行车模型(Bicycle Model)是对具有前轮转向的车辆建立的简化模型,被广泛应用于现代车辆的轨迹规划和控制,此模型假设车辆仅在水平面上运动、车轮运动方向沿着车轮旋转方向(即忽略横向位移),忽略前后轴载荷转移。本文基于自行车模型,推导车辆运动学和动力学方程。
2 车辆运动学推导
如图所示为自行车模型的几何关系,其中AAA、BBB分别表示前轮和后轮中心,CCC表示选定的车体中心,RRR是该中心对应的转向半径,CCC是瞬时转向中心(Instantaneous Center of Rotation, ICR),其定义为车辆前后轮速度垂线的交点,是车辆在转弯时所遵循的虚拟轨迹中心——转向轴。在车辆运动学中,ICR可以用来描述车辆的转向性能以及横向稳定性,能够帮助车辆设计师和工程师更好地优化车辆运动特性。δf\delta_fδf、δr\delta_rδr分别是前轮和后轮的转向角;β\betaβ是中心侧偏角;θ\thetaθ是车身航向角;lfl_flf、lrl_rlr分别是前轮和后轮距离 的距离;vvv是中心CCC的实际运动方向,vfv_fvf、vrv_rvr分别是前轮和后轮速度。
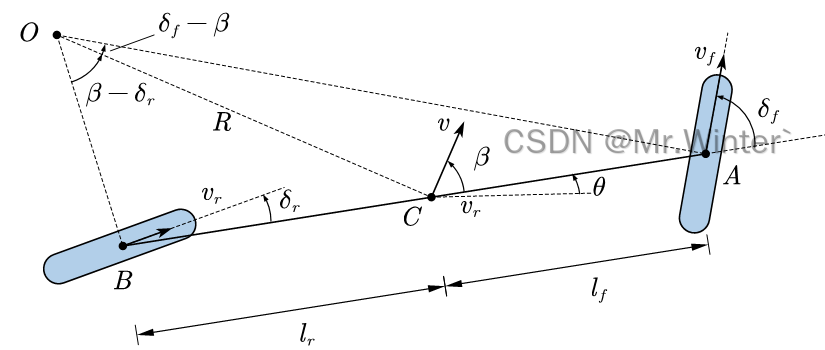
在ΔOBC\varDelta OBCΔOBC和ΔOAC\varDelta OACΔOAC中运用正弦定理可得
lfsin(δf−β)=Rsin(π2−δf),lrsin(β−δr)=Rsin(π2+δr)\frac{l_f}{\sin \left( \delta _f-\beta \right)}=\frac{R}{\sin \left( \frac{\pi}{2}-\delta _f \right)}, \frac{l_r}{\sin \left( \beta -\delta _r \right)}=\frac{R}{\sin \left( \frac{\pi}{2}+\delta _r \right)}sin(δf−β)lf=sin(2π−δf)R,sin(β−δr)lr=sin(2π+δr)R
整理可得前后轮几何方程
{lfR=tanδfcosβ−sinβlrR=sinβ−tanδrcosβ\begin{cases} \frac{l_f}{R}=\tan \delta _f\cos \beta -\sin \beta\\ \frac{l_r}{R}=\sin \beta -\tan \delta _r\cos \beta\\\end{cases}{Rlf=tanδfcosβ−sinβRlr=sinβ−tanδrcosβ
从该方程可以导出很多有用的推论:
-
中心侧偏角
将几何方程相减可整理得到
β=arctan(lrtanδf+lftanδrlf+lr)\beta =\mathrm{arc}\tan \left( \frac{l_r\tan \delta _f+l_f\tan \delta _r}{l_f+l_r} \right) β=arctan(lf+lrlrtanδf+lftanδr)
-
转向半径
将几何方程相加可整理得到
R=L(tanδf−tanδr)cosβR=\frac{L}{\left( \tan \delta _f-\tan \delta _r \right) \cos \beta}R=(tanδf−tanδr)cosβL
-
运动学方程
在全局坐标系xOyxOyxOy中车辆位姿表示为p=[xyθ]T\boldsymbol{p}=\left[ \begin{matrix} x& y& \theta\\\end{matrix} \right] ^Tp=[xyθ]T,则自行车模型运动学方程为
p˙=[x˙y˙θ˙]=vr[cosθsinθ(tanδf)/L]\boldsymbol{\dot{p}}=\left[ \begin{array}{c} \dot{x}\\ \dot{y}\\ \dot{\theta}\\\end{array} \right] =v_r\left[ \begin{array}{c} \cos \theta\\ \sin \theta\\ {{\left( \tan \delta _f \right)}/{L}}\\\end{array} \right] p˙=⎣⎡x˙y˙θ˙⎦⎤=vr⎣⎡cosθsinθ(tanδf)/L⎦⎤
其中vrv_rvr是后轮驱动速度,那么整个模型的输入控制量为u=[vrδf]T\boldsymbol{u}=\left[ \begin{matrix} v_r& \delta _f\\\end{matrix} \right] ^Tu=[vrδf]T
3 车辆横向动力学推导
在自行车运动学模型中,假设轮胎具有刚体性质,即车轮运动方向沿车轮旋转方向。但在高速行驶场合,由于侧向风或行驶向心力等因素造成车轮速度与其旋转方向不一致,导致原假设失效,因此需要考虑车轮的侧偏特性
本节采用最简单的线性侧偏力假设
Fα=CαF_{\alpha}=C\alpha Fα=Cα
其中FαF_\alphaFα是侧偏力,α\alphaα是侧偏角,CCC是侧偏刚度(负值)。规定α\alphaα在轮胎坐标系左侧为正。
首先以车体为惯性坐标系建模。如图所示,根据牛顿第二定律和刚体转动定律有
{may=Fαrcosδr+FαfcosδfIθ¨=Fαflfcosδf−Fαrlrcosδr\begin{cases} ma_y=F_{\alpha r}\cos \delta _r+F_{\alpha f}\cos \delta _f\\ I\ddot{\theta}=F_{\alpha f}l_f\cos \delta _f-F_{\alpha r}l_r\cos \delta _r\\\end{cases}{may=Fαrcosδr+FαfcosδfIθ¨=Fαflfcosδf−Fαrlrcosδr
其中III是车辆转动惯量。代入小转角假设以及侧偏力假设(两个轮胎)可得
{may=2Cαrαr+2CαfαfIθ¨=2Cαfαflf−2Cαrαrlr\begin{cases} ma_y=2C_{\alpha r}\alpha _r+2C_{\alpha f}\alpha _f\\ I\ddot{\theta}=2C_{\alpha f}\alpha _fl_f-2C_{\alpha r}\alpha _rl_r\\\end{cases}{may=2Cαrαr+2CαfαfIθ¨=2Cαfαflf−2Cαrαrlr
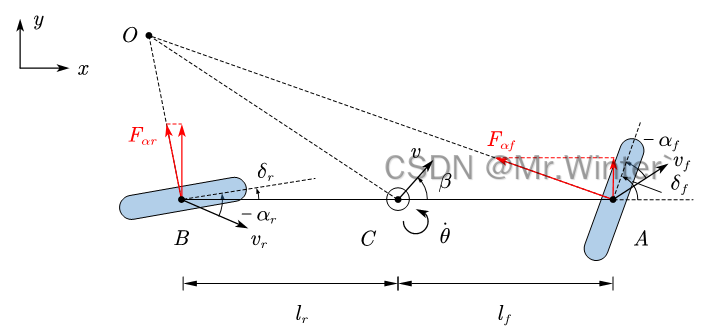
由于前后轮速度与车体速度方向的不一致,产生垂直于车身的相反转矩使车转动,由几何关系可得
{−αr=δr+θ˙lr−y˙vx−αf=δf−θ˙lf+y˙vx\begin{cases} -\alpha _r=\delta _r+\frac{\dot{\theta}l_r-\dot{y}}{v_x}\\ -\alpha _f=\delta _f-\frac{\dot{\theta}l_f+\dot{y}}{v_x}\\\end{cases}{−αr=δr+vxθ˙lr−y˙−αf=δf−vxθ˙lf+y˙
由于横向动力学不考虑控制纵向速度,因此vxv_xvx为定值。对于固结于车身的惯性系而言,不存在转动关系,因此需要将其转换到非惯性坐标系考察速度的变换情况,可以得到沿车身和垂直车身方向的速度变化量
{dvx=dvcosθ−vsinθdθdvy=dvsinθ+vcosθdθ\begin{cases} \mathrm{d}v_x=\mathrm{d}v\cos \theta -v\sin \theta \mathrm{d}\theta\\ \mathrm{d}v_y=\mathrm{d}v\sin \theta +v\cos \theta \mathrm{d}\theta\\\end{cases}{dvx=dvcosθ−vsinθdθdvy=dvsinθ+vcosθdθ
进一步对时间微分,采用小角度假设并忽略二阶项可得
{ax=v˙x−y˙θ˙ay=y¨+vxθ˙\begin{cases} a_x=\dot{v}_x-\dot{y}\dot{\theta}\\ a_y=\ddot{y}+v_x\dot{\theta}\\\end{cases}{ax=v˙x−y˙θ˙ay=y¨+vxθ˙
将aya_yay、αr\alpha_rαr、αf\alpha_fαf代入牛顿方程,考虑到后轮转角可以忽略不计,化简得到
ddt[yy˙θθ˙]=[010002(Cαr+Cαf)mvx02(Cαflf−2Cαrlr)mvx−vx000102(Cαflf−Cαrlr)Ivx02(Cαflf2+Cαrlr2)Ivx][yy˙θθ˙]+[0−2Cαfm0−2CαflfI]δf\frac{\mathrm{d}}{\mathrm{d}t}\left[ \begin{array}{c} y\\ \dot{y}\\ \theta\\ \dot{\theta}\\\end{array} \right] =\left[ \begin{matrix} 0& 1& 0& 0\\ 0& \frac{2\left( C_{\alpha r}+C_{\alpha f} \right)}{mv_x}& 0& \frac{2\left( C_{\alpha f}l_f-2C_{\alpha r}l_r \right)}{mv_x}-v_x\\ 0& 0& 0& 1\\ 0& \frac{2\left( C_{\alpha f}l_f-C_{\alpha r}l_r \right)}{Iv_x}& 0& \frac{2\left( C_{\alpha f}l_{f}^{2}+C_{\alpha r}l_{r}^{2} \right)}{Iv_x}\\\end{matrix} \right] \left[ \begin{array}{c} y\\ \dot{y}\\ \theta\\ \dot{\theta}\\\end{array} \right] +\left[ \begin{array}{c} 0\\ -\frac{2C_{\alpha f}}{m}\\ 0\\ -\frac{2C_{\alpha f}l_f}{I}\\\end{array} \right] \delta _fdtd⎣⎢⎢⎡yy˙θθ˙⎦⎥⎥⎤=⎣⎢⎢⎢⎡00001mvx2(Cαr+Cαf)0Ivx2(Cαflf−Cαrlr)00000mvx2(Cαflf−2Cαrlr)−vx1Ivx2(Cαflf2+Cαrlr2)⎦⎥⎥⎥⎤⎣⎢⎢⎡yy˙θθ˙⎦⎥⎥⎤+⎣⎢⎢⎡0−m2Cαf0−I2Cαflf⎦⎥⎥⎤δf
即为车辆基于线性侧偏假设的动力学模型
4 车辆横向动力学的误差形式
下面建立基于误差的横向动力学方程。设横向位移误差和航向角误差分别为e1e_1e1、e2e_2e2,道路曲率半径为RdR_dRd,则期望车辆转向半径也为RdR_dRd以实现沿路径行驶,所以车辆期望的横摆角速度为θ˙d=vx/Rd\dot{\theta}_{\mathrm{d}}={{v_x}/{R_{\mathrm{d}}}}θ˙d=vx/Rd,期望的横向加速度为ay,d=vx2/Rd=vxθ˙da_{y,\mathrm{d}}={{v_{x}^{2}}/{R_{\mathrm{d}}=v_x}}\dot{\theta}_{\mathrm{d}}ay,d=vx2/Rd=vxθ˙d,从而
e¨1=ay−ay,d=y¨+vx(θ˙−θ˙d)\ddot{e}_1=a_y-a_{y,\mathrm{d}}=\ddot{y}+v_x\left( \dot{\theta}-\dot{\theta}_{\mathrm{d}} \right) e¨1=ay−ay,d=y¨+vx(θ˙−θ˙d)
积分得到横向速度误差
e˙1=y˙+vx(θ−θd)\dot{e}_1=\dot{y}+v_x\left( \theta -\theta _{\mathrm{d}} \right) e˙1=y˙+vx(θ−θd)
航向误差则为
e2=θ−θde_2=\theta -\theta _{\mathrm{d}}e2=θ−θd
将第三节的动力学方程代入上述误差表达式化简得到其误差形式
ddt[e1e˙1e2e˙2]=[010002(Cαr+Cαf)mvx−2(Cαr+Cαf)m2(Cαflf−Cαrlr)mvx000102(Cαflf−Cαrlr)Ivx2(Cαrlr−Cαflf)I2(Cαflf2+Cαrlr2)Ivx][e1e˙1e2e˙2]+[0−2Cαfm0−2CαflfI]δf+[02(Cαflf−Cαrlr)mvx−vx02(Cαflf2+Cαrlr2)Ivx]θ˙d\frac{\mathrm{d}}{\mathrm{d}t}\left[ \begin{array}{c} e_1\\ \dot{e}_1\\ e_2\\ \dot{e}_2\\\end{array} \right] =\left[ \begin{matrix} 0& 1& 0& 0\\ 0& \frac{2\left( C_{\alpha r}+C_{\alpha f} \right)}{mv_x}& -\frac{2\left( C_{\alpha r}+C_{\alpha f} \right)}{m}& \frac{2\left( C_{\alpha f}l_f-C_{\alpha r}l_r \right)}{mv_x}\\ 0& 0& 0& 1\\ 0& \frac{2\left( C_{\alpha f}l_f-C_{\alpha r}l_r \right)}{Iv_x}& \frac{2\left( C_{\alpha r}l_r-C_{\alpha f}l_f \right)}{I}& \frac{2\left( C_{\alpha f}l_{f}^{2}+C_{\alpha r}l_{r}^{2} \right)}{Iv_x}\\\end{matrix} \right] \left[ \begin{array}{c} e_1\\ \dot{e}_1\\ e_2\\ \dot{e}_2\\\end{array} \right] \\+\left[ \begin{array}{c} 0\\ -\frac{2C_{\alpha f}}{m}\\ 0\\ -\frac{2C_{\alpha f}l_f}{I}\\\end{array} \right] \delta _f+\left[ \begin{array}{c} 0\\ \frac{2\left( C_{\alpha f}l_f-C_{\alpha r}l_r \right)}{mv_x}-v_x\\ 0\\ \frac{2\left( C_{\alpha f}l_{f}^{2}+C_{\alpha r}l_{r}^{2} \right)}{Iv_x}\\\end{array} \right] \dot{\theta}_{\mathrm{d}}dtd⎣⎢⎢⎡e1e˙1e2e˙2⎦⎥⎥⎤=⎣⎢⎢⎢⎡00001mvx2(Cαr+Cαf)0Ivx2(Cαflf−Cαrlr)0−m2(Cαr+Cαf)0I2(Cαrlr−Cαflf)0mvx2(Cαflf−Cαrlr)1Ivx2(Cαflf2+Cαrlr2)⎦⎥⎥⎥⎤⎣⎢⎢⎡e1e˙1e2e˙2⎦⎥⎥⎤+⎣⎢⎢⎡0−m2Cαf0−I2Cαflf⎦⎥⎥⎤δf+⎣⎢⎢⎢⎡0mvx2(Cαflf−Cαrlr)−vx0Ivx2(Cαflf2+Cαrlr2)⎦⎥⎥⎥⎤θ˙d
接着可以基于该方程实现LQR、MPC等控制算法
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …
