当前位置：首页 > news >正文

深入级联不稳定性：从 Lipschitz 连续性视角探讨图像恢复与目标检测的协同作用

news 2025/11/4 8:28:42

摘要

https://arxiv.org/pdf/2510.24232v1
为了提高检测器在恶劣条件（例如，雾霾和低光照）下的鲁棒性，通常将图像恢复作为预处理步骤，以增强图像质量供检测器使用。然而，恢复网络与检测网络之间的功能不匹配会引入不稳定性，并阻碍有效的集成——这一问题尚未得到充分探索。我们通过 Lipschitz 连续性的视角重新审视这一局限性，分析了恢复网络和检测网络在输入空间和参数空间中的功能差异。我们的分析表明，恢复网络执行平滑、连续的变换，而目标检测器则具有不连续的决策边界，对微小扰动高度敏感。这种不匹配在传统的级联框架中引入了不稳定性，其中来自恢复过程的即使不可察觉的噪声也会在检测阶段被放大，破坏梯度流并阻碍优化。为了解决这个问题，我们提出了 Lipschitz 正则化目标检测（LROD），这是一个简单而有效的框架，它将图像恢复直接集成到检测器的特征学习中，在训练期间协调两个任务的 Lipschitz 连续性。我们将此框架实现为 Lipschitz 正则化 YOLO（LR-YOLO），它可以无缝地扩展到现有的 YOLO 检测器。在雾霾和低光照基准上的大量实验证明，LR-YOLO 持续提高了检测稳定性、优化平滑度和整体准确性。

1 引言

恶劣的成像条件会通过引起各种图像退化（包括对比度降低、边缘模糊和物体边界遮挡）给目标检测带来挑战。缓解此问题的典型方法是采用图像恢复作为预处理步骤，旨在在检测之前提高图像质量[1, 2, 3]。然而，其有效性受到恢复网络和检测网络之间功能不匹配的限制。这种不一致性会引入不稳定性，其中在恢复过程中引入的不可察觉的噪声在检测过程中被放大，导致不可靠的预测[4, 5]。此外，这些任务之间的根本差异仍未得到充分探索，阻碍了更好的集成和增强鲁棒性的机会。为了弥合这一差距，理解它们的功能行为对于实现有效的协同至关重要。为此，我们通过 Lipschitz 连续性的视角分析了传统的“图像恢复→目标检测”级联框架，重点关注两个方面：输入空间和参数空间。

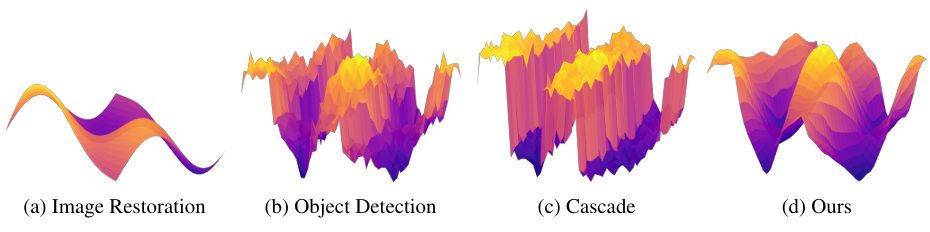
在这里插入图片描述

图1：在网络输入扰动下的功能行为可视化。(a) 图像恢复网络表现出平滑、连续的映射，输入的变化会导致输出的逐渐调整。(b) 目标检测网络由于分类和边界框回归中的突变决策边界而显示出尖锐的不连续性。© 级联框架（图像恢复 $→\rightarrow$ 目标检测）放大了不稳定性，导致输出呈现碎片化和非平滑行为。(d) 我们的方法将低 Lipschitz 的图像恢复集成到高 Lipschitz 的目标检测的特征学习中，促进了更平滑的过渡并增强了稳定性。

从输入空间的角度来看，我们利用 Lipschitz 连续性的概念，该概念刻画了模型输出对输入扰动的敏感性[6]。具有较低 Lipschitz 常数的网络表现出更平滑、更可预测的变化，而较高的常数则表明敏感性高且不稳定。通过计算相对于雾霾密度变化的雅可比范数[7]，我们观察到目标检测网络的 Lipschitz 常数比恢复网络的大近一个数量级，突显了其平滑度要低得多。这种差异凸显了它们功能行为的不同。恢复网络表现出平滑、连续的映射，其中小的输入扰动会导致恢复图像的逐渐和可预测的调整。这种平滑性源于对像素的逐点处理，它一致地增强局部区域并将变化平滑地传播到整个图像。相比之下，目标检测网络本质上是不连续的，其分类和边界框回归具有尖锐的决策边界。即使是微小的像素级变化也可能导致类别预测或边界框坐标的突然变化，反映出输出中的非平滑、阶梯状过渡。这种行为上的鲜明对比在两个网络级联时会导致不稳定性。为了进一步说明这种差异，我们在图1(a)和(b)中可视化了功能行为，其中恢复的平滑过渡与检测中观察到的突然变化形成鲜明对比。这种不一致性在两个网络级联时引入了不稳定性：恢复过程中引入的不可察觉的噪声在检测过程中被放大，导致级联框架的整体非平滑行为，如图1©所示。

为了进一步理解在传统的“图像恢复→目标检测”级联框架中观察到的不稳定性，我们将分析扩展到网络的参数空间，在该空间中，Lipschitz 连续性刻画了模型输出对其参数变化的敏感性。我们的研究发现，图像恢复网络保持相对较低的 Lipschitz 常数，从而在训练期间产生平滑且稳定的优化轨迹。相比之下，目标检测网络表现出高得多的 Lipschitz 常数，导致梯度的急剧变化和不稳定的收敛路径。这种不平衡破坏了梯度流，引入了相互干扰，并使联合优化变得不稳定，进一步加剧了传统级联框架的不稳定性。

鉴于网络稳定性在恶劣条件下的重要性，一个关键挑战在于协调图像恢复和目标检测，以解决 Lipschitz 连续性固有的差异。为了解决这个问题，我们提出了 Lipschitz 正则化目标检测（LROD），这是一个简单而有效的框架，它将图像恢复直接集成到检测器的特征学习中。与传统的级联不同，LROD 在训练期间协调两个任务的 Lipschitz 连续性，在扰动通过检测器的不连续层传播之前对其进行平滑。这种耦合减轻了噪声放大，在具有挑战性的环境中增强了稳定性。此外，LROD 引入了一个参数空间正则化项来稳定梯度流，确保更平滑的优化动态，并在不同退化强度下提高鲁棒性。

我们将其 LROD 集成到现有的 YOLO 检测器中，利用它们的实时性能、资源效率和适用于边缘部署的优势。这种集成产生了一种高效的模型，称为 Lipschitz 正则化 YOLO（LR-YOLO），它可以无缝地应用于 YOLO 系列检测器（例如，YOLOv10 [8] 和 YOLOv8 [9]）。如图1(d)所示，我们提出的 Lipschitz 正则化目标检测相比于级联框架实现了更平滑的 Lipschitz 连续性。在图像去雾和低光增强基准上的大量实验证明，与传统的级联框架相比，LR-YOLO 提高了检测的稳定性和鲁棒性。总结来说，我们的贡献如下：

Lipschitz 连续性分析：我们对图像恢复和目标检测网络在输入空间和参数空间中的 Lipschitz 连续性进行了详细分析。我们的分析揭示了这两个任务在平滑性上的关键不匹配，这可能会引入不稳定性并阻碍有效集成。据我们所知，这是早期致力于通过 Lipschitz 连续性分析来理解级联检测管道中不稳定性挑战的工作。

Lipschitz 正则化框架：受我们分析的启发，我们提出了一种简单有效的目标检测框架，该框架将图像恢复直接集成到检测器的特征学习中，在训练期间协调两个任务的 Lipschitz 连续性。这种设计增强了平滑性，并减轻了传统级联方法固有的不稳定性。

2 相关工作

恶劣条件下的目标检测。现有研究主要集中在级联框架上，其中图像恢复技术，如图像去雾[10, 11]、低光增强[12, 13]和一体化恢复[14]，被用作预处理步骤，以提高图像质量，并与领域自适应方法[15]相比增强人类对检测结果的信任。ReForDe [2] 使用对抗训练为微调恢复网络生成对检测友好的标签。SR4IR [16] 引入了一个训练框架，其中图像恢复受到目标检测的约束，并且检测训练利用恢复的输出。图像自适应技术[1, 3]将可微图像处理滤波器集成到检测管道中。FeatEnHancer[17]应用分层特征增强来提高检测性能。尽管有这些进步，恢复网络和检测网络之间的功能不匹配仍未得到充分探索。我们的工作报告指出，这两个任务之间 Lipschitz 连续性的巨大差异在它们级联时加剧了非平滑性，导致在不同退化强度下的不稳定性。为了解决这个问题，我们提出了一个 Lipschitz 正则化框架，该框架增强了检测网络的 Lipschitz 连续性，促进了这两个任务之间更好的协调。

Lipschitz 连续性分析。Lipschitz 连续性在分析深度神经网络的稳定性和鲁棒性方面非常有用[18, 19, 20]。具有较低 Lipschitz 常数的模型往往在对抗条件下表现出更好的泛化性能[21]。这激发了对正则化技术的进一步研究，这些技术通过约束 Lipschitz 常数来增强模型的鲁棒性。例如，SN-GAN [22] 通过限制网络参数的谱范数来控制 Lipschitz 常数，而其他基于 Lipschitz 的正则化技术已被提出以提高模型稳定性[23]。几项研究已将这些思想扩展到网络设计[24]，突显了 Lipschitz 连续性在控制神经网络平滑性和稳定性方面的关键作用。在我们的工作中，我们使用 Lipschitz 连续性作为调查视角，从输入空间和参数空间分析恶劣条件下目标检测的稳定性。我们证明了图像恢复和目标检测网络之间 Lipschitz 连续性的差异是级联框架中非平滑性和不稳定性的主要来源。
在这里插入图片描述

3 Lipschitz 连续性视角

3.1 输入空间分析：恶劣条件下的模型稳定性

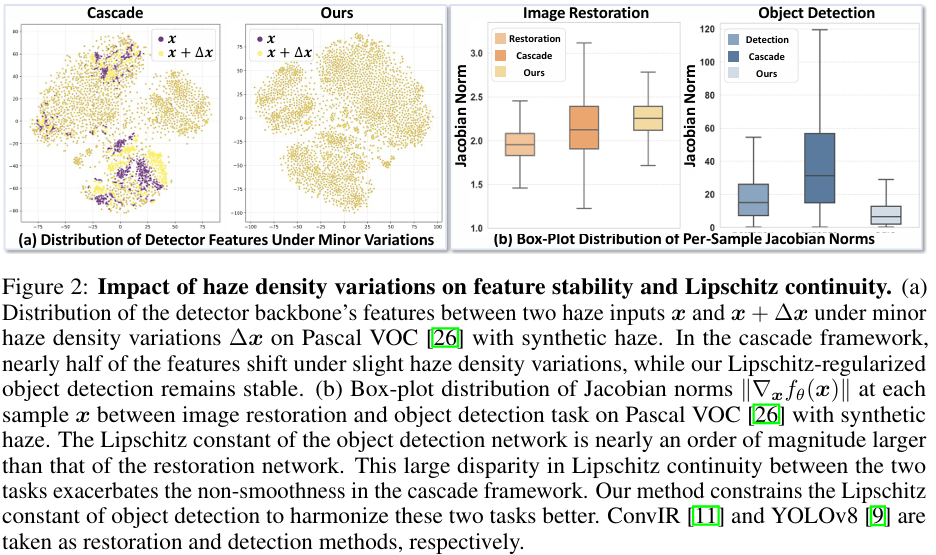
在雾霾或低光等恶劣条件下，目标检测对退化强度的变化（包括雾霾密度和亮度波动的变化）高度敏感。传统的“图像恢复→目标检测”级联框架在应对这些变化时表现不佳，导致检测结果不稳定。如图2(a)所示，即使通过恢复部分缓解，微小的扰动仍然会导致检测器特征的显著变化，暴露了该框架的不稳定性。为了解释这一点，我们通过 Lipschitz 连续性的视角进行分析，它量化了模型对输入变化的敏感性。我们的研究发现，检测网络的 Lipschitz 常数比恢复网络的大近一个数量级，在恶劣条件下放大噪声并破坏稳定性。

图2：雾霾密度变化对特征稳定性和 Lipschitz 连续性的影响。(a) 在两个雾霾输入 $x$ 和 $x+\Delta x$ 下检测器主干特征的分布：在级联框架中，轻微的雾霾密度变化 $\Delta x$ 就会导致近一半的特征发生偏移，而我们的 Lipschitz 正则化目标检测保持稳定。(b) 在 Pascal VoC [26] 数据集上，图像恢复和目标检测任务在每个样本 $x$ 处的雅可比范数 $\|\nabla_{x}f_{\theta}(x)\|$ 的箱线图分布。目标检测网络的 Lipschitz 常数比恢复网络的大近一个数量级。这两个任务之间 Lipschitz 连续性的巨大差异加剧了级联框架中的非平滑性。我们的方法通过约束检测的 Lipschitz 常数来更好地协调这两个任务。ConvIR [11] 和 YOLOv8 [9] 分别被用作恢复和检测方法。

我们首先回顾 Lipschitz 连续性的定义：一个网络 $f(⋅;θ):RD↦RKf(\cdot;\theta):\mathbb{R}^{D}\mapsto\mathbb{R}^{K}$ ，定义在某个域 $dom(f)⊆RD\text{dom}(f)\subseteq\mathbb{R}^{D}$ 上，参数为 $θ\theta$ ，如果存在一个实常数 $C > 0$ ，使得对于所有 $x1,x2∈dom(f)\boldsymbol{x}_{1}, \boldsymbol{x}_{2} \in \text{dom}(f)$ 都有 $∥f(x1;θ)−f(x2;θ)∥p≤C∥x1−x2∥p\|f(\boldsymbol{x}_{1};\theta)-f(\boldsymbol{x}_{2};\theta)\|_{p} \leq C\|\boldsymbol{x}_{1}-\boldsymbol{x}_{2}\|_{p}$ ，则称该网络为 $C$ -Lipschitz 连续的。为简化起见，我们将在本文的其余部分计算2-范数（记为 $∥⋅∥\|\cdot\|$ ），这可以很容易地推广到其他范数。根据 [25] 中的定理1，我们知道对于一个可微的 $C$ -Lipschitz 连续网络 $f(⋅;θ):RD↦RKf(\cdot;\theta):\mathbb{R}^{D}\mapsto\mathbb{R}^{K}$ ， $f(⋅;θ)f(\cdot;\theta)$ 的 Lipschitz 常数可以表示为 $Cx(f(x;θ))^=sup⁡x∈dom(f)∥∇xf(x;θ)∥∗=sup⁡x∈dom(f)∥∇xf(x;θ)∥\hat{C_{\boldsymbol{x}}(f(\boldsymbol{x};\theta))}=\sup_{\boldsymbol{x}\in \text{dom}(f)}\|\nabla_{\boldsymbol{x}}f(\boldsymbol{x};\theta)\|_{*}=\sup_{\boldsymbol{x}\in \text{dom}(f)}\|\nabla_{\boldsymbol{x}}f(\boldsymbol{x};\theta)\|$ ，其中 $∇xf(x;θ)\nabla_{\boldsymbol{x}}f(\boldsymbol{x};\theta)$ 是 $f$ 关于输入 $x\boldsymbol{x}$ 的雅可比矩阵， $∥⋅∥∗\|\cdot\|_{*}$ 表示对偶范数（2-范数的对偶范数是其本身）。

为了定量评估图像恢复和目标检测网络的 Lipschitz 常数，我们在 Pascal VOC 数据集 [26] 的每个样本 $x$ 上计算上述雅可比范数，考虑雾霾密度的变化。如图2(b)所示，我们观察到图像恢复网络的雅可比范数在每个样本上介于1到3.5之间，而目标检测网络的雅可比范数比图像恢复网络的大近一个数量级。这表明目标检测的 Lipschitz 常数比图像恢复的高。因此，这两个任务之间 Lipschitz 连续性的巨大差异导致它们在直接级联时产生一个不稳定的框架。具体来说，即使是微小的变化也必然会被恢复网络放大（因为其每个样本的雅可比范数超过1），并被级联框架内高 Lipschitz 常数的检测网络进一步去稳定化。

备注1。从 Lipschitz 连续性的角度来看，图像恢复网络表现出平滑和连续的映射，而目标检测网络则更为非平滑。这两个任务之间 Lipschitz 连续性的巨大差异在它们直接级联时加剧了非平滑性，导致在退化强度变化下的不稳定性。

3.2 参数空间分析：训练稳定性

恢复网络和检测网络之间 Lipschitz 连续性的差异不仅存在于输入空间，还影响它们的训练稳定性。为了理解这一点，我们分析了网络的参数空间，以捕捉梯度更新如何在优化过程中影响模型稳定性。我们的分析表明，具有较低 Lipschitz 常数的恢复网络保持平滑的优化轨迹，而具有高得多的 Lipschitz 常数的检测网络则经历急剧的梯度变化和不稳定的收敛。这种不平衡破坏了梯度流，导致基于级联设计的训练不稳定。

在这里插入图片描述

图3：级联框架与我们提出的 Lipschitz 正则化目标检测在参数空间平滑性和优化稳定性方面的比较。(a) 恢复和检测任务的损失曲面：恢复网络表现出平滑的轨迹，而检测网络遇到急剧的梯度变化，表明不稳定。(b) 级联框架放大了这种不平衡，导致收敛效率低下和振荡的优化路径。(c) 我们的方法引入了 Lipschitz 正则化来平滑目标检测的参数空间，增强了稳定性并使其与恢复任务相协调。ConvIR [11] 和 YOLOv8 [9] 分别被用作代表性的恢复和检测方法。

我们将 Lipschitz 连续性分析扩展到参数空间：如果存在 $Cθ(f(x;θ~))>0C_{\theta}(f(\boldsymbol{x};\tilde{\theta}))>0$ ，使得对于所有 $θ1,θ2∈Θ\theta_1, \theta_2 \in \Theta$ 都有 $∥f(x;θ1)−f(x;θ2)∥≤Cθ(f(x;θ))∥θ1−θ2∥\|f(\boldsymbol{x};\theta_1)-f(\boldsymbol{x};\theta_2)\| \leq C_{\theta}(f(\boldsymbol{x};\theta)) \|\theta_1-\theta_2\|$ ，则称定义在某个参数空间 $Θ\Theta$ 上的网络 $f(x;θ)f(\boldsymbol{x};\theta)$ 在参数空间中是 Lipschitz 连续的。由于 $x$ 和 $θ\theta$ 之间的对称性，当两个变量互换时，类似的结论成立：定义在参数空间 $Θ\Theta$ 上的 $f(x;θ)f(\boldsymbol{x};\theta)$ 的参数空间 Lipschitz 常数可以表示为 $Cθ(f(x;θ))=sup⁡θ∈Θ∥∇θf(x;θ˚)∥C_{\theta}(f(\boldsymbol{x};\theta)) = \sup_{\theta\in\mathbf{\Theta}}\|\nabla_{\theta}f(\boldsymbol{x};\mathring{\theta})\|$ ，其中 $∇θf(x;θ)\nabla_{\theta}f(\pmb{x};\theta)$ 表示参数空间中网络参数的梯度。

鉴于网络使用梯度下降优化算法进行训练，表达为 $θ←θ−μ⋅∇θf(x;θ)\theta\leftarrow\theta-\mu\cdot\nabla_{\theta}f(\pmb{x};\theta)$ （其中 $μ\mu$ 表示学习率），参数空间中的 Lipschitz 常数对于确保训练稳定性至关重要。这是因为参数空间中的 Lipschitz 常数在训练过程中充当了网络参数梯度的上界。

参数空间中的 Lipschitz 连续性反映了模型输出对其参数变化的敏感性。为了说明这一点，我们通过沿两个方向扰动参数来可视化损失曲面，揭示它们对优化平滑性和稳定性的影响。具体来说，我们使用 [27] 中的可视化方法：设 $θ\theta$ 表示固定的模型参数，我们在参数空间中选择两个归一化的方向向量 $δ\delta$ 和 $η\eta$ ，并绘制函数 $f(α,β)=L(θ+αδ+βη)f(\alpha,\beta)=\mathcal{L}(\theta+\alpha\delta+\beta\eta)$ 的曲面，其中 $L\mathcal{L}$ 是损失函数， $α\alpha$ 和 $β\beta$ 是曲面上的坐标。

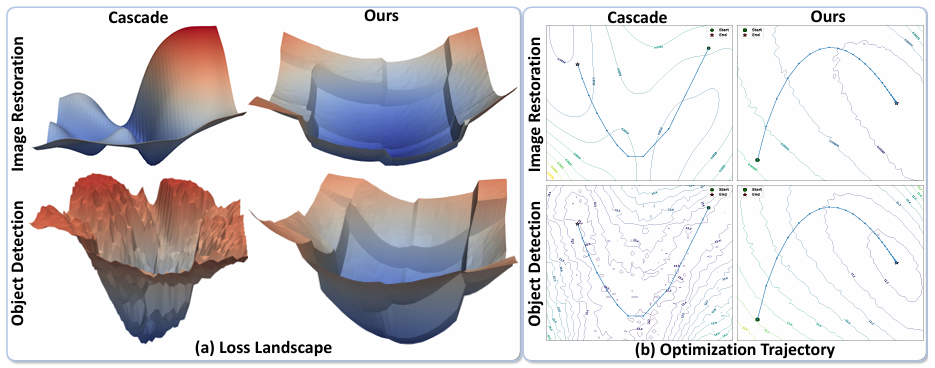
如图3(a)所示，图像恢复网络的损失曲面显示出平滑的损失函数，而目标检测网络的损失曲面则明显粗糙。这反映了它们在参数空间中 Lipschitz 常数的差异：恢复网络倾向于具有较低的 Lipschitz 常数，产生更平滑的梯度，而检测网络则表现出较高的 Lipschitz 常数，显示出更尖锐的过渡，并对参数变化更敏感。图3(b)进一步说明了优化轨迹，其中恢复遵循稳定的路径，而检测则经历频繁的偏移，表明不稳定。这种不平衡在联合训练期间破坏了梯度流，导致不稳定收敛和降低的优化效率。

备注2。具有较低 Lipschitz 常数的图像恢复网络表现出平滑的优化轨迹，而具有较高 Lipschitz 常数的目标检测网络则经历急剧的梯度变化和不稳定的收敛。这两个任务在参数空间中的这种不平衡导致了基于级联设计的训练不稳定和优化效率降低。

4 Lipschitz 正则化目标检测

第3节的分析揭示了恢复网络和检测网络之间 Lipschitz 连续性的差异，这种差异在输入空间和参数空间中都有体现。受此驱动，我们提出了 Lipschitz 正则化目标检测（LROD），这是一个简单而有效的框架，通过有针对性的 Lipschitz 正则化来协调恢复和检测。具体来说，LROD 引入了两个核心机制：1) 通过低 Lipschitz 恢复进行 Lipschitz 正则化，以约束输入空间中目标检测的 Lipschitz 常数；2) 通过参数空间平滑进行 Lipschitz 正则化，以约束参数空间中的 Lipschitz 常数。

4.1 通过低 Lipschitz 恢复进行 Lipschitz 正则化

输入空间中的 Lipschitz 连续性分析（第3.1节）表明，图像恢复网络表现出平滑、连续的映射，而目标检测网络则更为非平滑。通过利用恢复任务的低 Lipschitz 特性，我们将恢复学习集成到检测器主干的特征学习中，从而约束输入空间中目标检测任务的 Lipschitz 常数。这更好地使检测任务与低 Lipschitz 恢复任务相协调。

备注3（通过低 Lipschitz 恢复进行 Lipschitz 正则化）。令： $fθb,θd=fθd∘fθbf_{\theta_{b},\theta_{d}}=f_{\theta_{d}}\circ f_{\theta_{b}}$ 表示目标检测模型，其中 $fθb(⋅;θb)f_{\theta_{b}}(\cdot;\theta_{b})$ 是由 $θb\theta_{b}$ 参数化的主干网络， $fθd(⋅;θd)f_{\theta_{d}}(\cdot;\theta_{d})$ 是由 $θd\theta_{d}$ 参数化的检测头。类似地，令： $gθb,θr=fθr∘fθbg_{\theta_{b},\theta_{r}}=f_{\theta_{r}}\circ f_{\theta_{b}}$ 表示图像恢复模型，其中 $fθr(⋅;θr)f_{\theta_{r}}(\cdot;\theta_{r})$ 是由 $θr\theta_{r}$ 参数化的恢复头，共享相同的主干 $fθbf_{\theta_{b}}$ 。给定检测损失和恢复损失的加权组合：
$L(θb,θd,θr)=Ldet(fθb,θd)+λ⋅Lres(gθb,θr),λ>0\mathcal{L}(\theta_{b},\theta_{d},\theta_{r})=\mathcal{L}_{\mathrm{det}}(f_{\theta_{b},\theta_{d}})+\lambda\cdot\mathcal{L}_{\mathrm{res}}(\boldsymbol{g}_{\theta_{b},\theta_{r}}),\quad\lambda>0$
令 $Lip⁡(fθb):=sup⁡x∥Jfθb(x)∥\operatorname{Lip}(f_{\theta_{b}}):=\sup_{\pmb{x}}\|J_{f_{\theta_{b}}}(\pmb{x})\|$ 为由雅可比范数定义的 $fθbf_{\theta_{b}}$ 的 Lipschitz 常数。如果：

$Lres\mathcal{L}_{\mathrm{res}}$ 是 Lipschitz 连续的，并且 $∥∇θbLres(gθb,θr)∥≤G\|\nabla_{\theta_{b}}\mathcal{L}_{\mathrm{res}}(\boldsymbol{g}_{\theta_{b},\theta_{r}})\| \leq G$ ，其中 $\|\nabla_{\theta_{b}}\mathcal{L}_{\mathrm{det}}(f_{\theta_{b},\theta_{d}})\|$ ；
存在一个训练样本 $x⋆\boldsymbol{x}^{\star}$ 和 $γ>0\gamma>0$ ，使得： $⟨∇θb∥Jfθb(x⋆)∥,∇θbLres(gθb,θr)⟩≥γ\left\langle \nabla_{\theta_{b}}\|J_{f_{\theta_{b}}}(\boldsymbol{x}^{\star})\|, \nabla_{\theta_{b}}\mathcal{L}_{\mathrm{res}}(\boldsymbol{g}_{\theta_{b},\theta_{r}})\right\rangle \geq \gamma$ ，
那么在连续时间梯度下降 $θb(t+1)←θb(t)−μ⋅∇θbL(θb,θd,θr){\theta_{b}}^{(t+1)}\leftarrow{\theta_{b}}^{(t)}-\mu\cdot\nabla_{\theta_{b}}\mathcal{L}(\theta_{b},\theta_{d},\theta_{r})$ （ $μ\mu$ 表示学习率）下，Lipschitz 常数的演化满足：
$ddt[Lip(fθb)]≤−λ⋅γ+ξ(t)\frac{d}{d t}\left[\mathrm{Lip}(f_{\theta_{b}})\right]\leq-\lambda\cdot\gamma+\xi(t)$
其中 $ξ(t):=⟨∇θb∥Jfθb(x⋆)∥,∇θbLdet(fθb,θd)⟩\xi(t) := \left\langle \nabla_{\theta_{b}}\|J_{f_{\theta_{b}}}(\pmb{x}^{\star})\|, \nabla_{\theta_{b}}\mathcal{L}_{\mathrm{det}}(f_{\theta_{b},\theta_{d}})\right\rangle$ 是由检测损失引起的无约束变化， $γ\gamma$ 是通过恢复任务实现的正则化。

这表明，通过共享检测器的主干，将图像恢复任务直接集成到检测器的特征学习中，有助于在训练期间抑制模型对输入扰动的敏感性，有效地起到 Lipschitz 正则化的作用。详细证明见附录A。

具体来说，我们从检测器主干的前三个阶段提取低级特征，这些特征保留了图像恢复所必需的基本空间和纹理信息。然后，这些特征通过一个特定于恢复的头来获得恢复后的图像。通过利用图像恢复任务固有的更平滑的 Lipschitz 连续性，这种恢复损失在训练期间隐式地正则化了用于目标检测的特征表示，从而约束了输入空间中检测网络的 Lipschitz 常数。如图2(a)和(b)所示，我们提出的 Lipschitz 正则化目标检测相比于原始目标检测和级联框架表现出更平滑的 Lipschitz 连续性，在不同退化强度下具有更低的 Lipschitz 常数和更稳定的检测器特征。

4.2 通过参数空间平滑进行 Lipschitz 正则化

参数空间中的 Lipschitz 连续性分析（第3.2节）表明，低 Lipschitz 的恢复网络保持平滑的优化轨迹，而高 Lipschitz 的检测网络则经历急剧的梯度变化和不稳定的收敛。为了改善这些任务之间的协调性并确保训练稳定性，我们约束了检测网络在参数空间中的 Lipschitz 常数。我们引入了一个参数空间正则化项来稳定梯度流，促进更平滑的优化动态。

备注4（通过参数空间平滑进行 Lipschitz 正则化）。令 $θ=θb∪θd\theta=\theta_{b}\cup\theta_{d}$ 为检测模型的完整参数集。参数空间正则化项定义为关于模型参数的梯度范数，记为 $∥∇θfθ(x)∥\|\nabla_{\theta}f_{\theta}({\pmb x})\|$ 。

完整框架。Lipschitz 正则化目标检测（LROD）框架结合了上述两种正则化，以确保稳定和高效的训练。总损失函数定义为：
$Ltotal=Ldet+λ⋅Lres+λp⋅∥∇θfθ(x)∥,\mathcal{L}_{\mathrm{total}}=\mathcal{L}_{\mathrm{det}}+\lambda\cdot\mathcal{L}_{\mathrm{res}}+\lambda_{p}\cdot\left\|\nabla_{\theta}f_{\theta}(\boldsymbol{x})\right\|,$
其中 $Ldet\mathcal{L}_{\mathrm{det}}$ 是检测损失， $Lres\mathcal{L}_{\mathrm{res}}$ 是恢复损失，计算为恢复图像与真实干净图像之间的 Charbonnier 损失 [28]， $∥∇θfθ(x)∥\|\nabla_{\theta}f_{\theta}({\pmb x})\|$ 是正则化项。权重 $λ\lambda$ 和 $λp\lambda_{p}$ 分别用于平衡恢复项和正则化项。我们将此框架实现为 Lipschitz 正则化 YOLO（LR-YOLO），它基于 YOLO 检测器构建。如图3所示，ConvIR [11] 和 YOLOv8 [9] 分别被用作代表性的恢复和检测方法。与传统的级联框架相比，LR-YOLO 平滑了目标检测的损失曲面，使其在训练期间更好地与图像恢复对齐。这带来了平滑的梯度流、改进的稳定性以及更高效的优化。

5 实验

5.1 实验设置

数据集。数据集涵盖两种具有挑战性的条件：雾天和低光环境。对于这两种设置，我们使用 Pascal VOC [26] 和 COCO [29] 数据集进行训练和验证，遵循[1, 2, 5]中的退化设置，并使用真实世界数据集进行域外评估。

训练和验证数据：
a) VOC_Haze_Train 和 VOC_Haze_Val 分别包含 8,111 和 2,734 张图像。雾霾在训练期间使用大气散射模型在线合成， $β∈[0.5,1.5]\beta\in[0.5,1.5]$ ，而验证图像则离线合成一次以保证可重现性；
b) VOC_Dark_Train 和 VOC_Dark_Val 分别包含 12,334 和 3,760 张图像。低光在训练期间通过伽马校正在线模拟，在验证时离线进行， $γ∈[1.5,5]\gamma\in[1.5,5]$ 。雾霾和低光条件下训练和验证数据集中的类别与真实世界数据集中的类别一致；
c) COCO_Haze_Train 和 COCO_Dark_Train 包含 118,287 张训练图像，COCO_Haze_Val 和 COCO_Dark_Val 包含 5,000 张验证图像。
真实世界测试数据。我们采用两个基准数据集进行域外评估：
a) RTTS [30] 包含 4,322 张真实世界雾霾图像，标注了5个物体类别，即：人、汽车、公共汽车、自行车和摩托车；
b) ExDark [31] 包含 2,563 张真实世界低光图像，标注了10个类别，即：人、汽车、公共汽车、自行车、摩托车、船、瓶子、椅子、狗和猫。

评估指标。我们使用平均精度均值（mAP）在 IoU 阈值为 50% 的情况下评估目标检测性能，该指标默认排除了困难物体。此外，我们还报告了 $mAPdifficult\mathbf{mAP_{\mathrm{difficult}}}$ ，它包括 Pascal VOC [26] 和 RTTS [30] 数据集上的所有物体，包括具有挑战性的情况（例如，被遮挡的目标）。对于 COCO 数据集 [29]，我们采用标准的 COCO 风格指标，包括在 IoU 阈值从 0.5 到 0.95（以 0.05 为增量）下的 mAP 平均值，以及 $AP50,AP75\mathrm{AP_{50}, AP_{75}}$ 和按尺度划分的分数： $APS\mathrm{AP}_{S}$ （小）、 $APM\mathbf{AP}_{M}$ （中）和 $APL\mathrm{AP}_{L}$ （大）。

实现细节：我们采用 YOLOv10-s 和 YOLOv8-s 作为基线检测器。对于训练，损失权重设置为 $λ=10\lambda=10$ 和 $λp=0.01\lambda_p=0.01$ 。我们使用 SGD 优化器，初始学习率为 $1×10−21\times10^{-2}$ ，权重衰减为 $5×10−45\times10^{-4}$ 。模型在 RTX 4090 GPU 上训练 100 个周期，批大小为 16，大约需要 8 小时。输入图像被调整为 $640×640\mathrm{640\times640}$ ，并应用标准的 YOLO 数据增强技术（例如，随机翻转和仿射变换）。对于 COCO 数据集上的实验，我们使用 8 个 RTX 4090 GPU，每个 GPU 的批大小为 16。训练进行 300 个周期，大约需要 48 小时。

5.2 恶劣条件下的目标检测

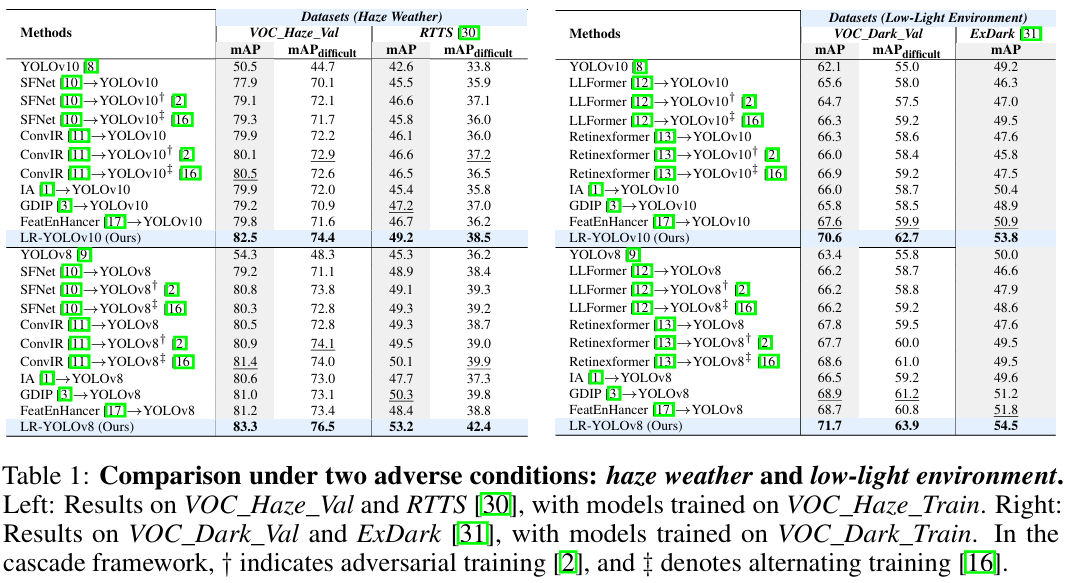
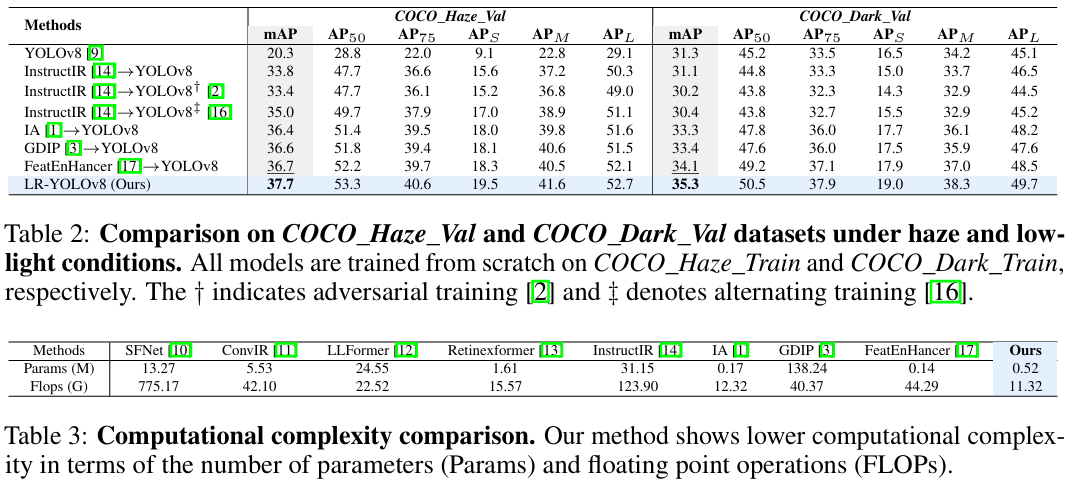
表1展示了在两种恶劣条件下（雾天和低光环境）的目标检测方法比较。雾天在 $VOC_Haze_Val\mathit{VOC\_Haze\_Val}$ 和 RTTS [30] 数据集上评估，低光环境在 $VOC_Dark_Val\mathit{VOC\_Dark\_Val}$ 和 ExDark [31] 数据集上评估。我们比较了各种图像恢复方法，包括 SFNet[10]、ConvIR [11]、LLFormer [12] 和 RetinexFormer [13]，这些方法均在退化图像上进行训练，并用于在检测前恢复输入。我们进一步考虑了两种联合训练策略：1) 对抗训练 [2]，其中恢复网络被微调以生成对检测友好的图像；2) 交替训练[16]，其中恢复使用检测驱动的感知损失进行监督，检测则在恢复后的输出上进行训练。此外，我们还包含了端到端方法进行比较，包括 IA [1]、GDIP [3] 和 FeatEnHancer [17]。它们直接在退化输入上进行训练。所有模型均分别在 $VOC_Haze_Train\mathit{VOC\_Haze\_Train}$ 和 $VOC_Dark_Train\mathit{VOC\_Dark\_Train}$ 数据集上从头开始训练。我们的方法在使用 YOLOv10 和 YOLOv8 作为目标检测器时都优于其他方法，在 RTTS 上分别实现了 2.0 和 2.9 的 mAP 提升，在 ExDark 上分别实现了 2.9 和 2.7 的提升。表2展示了在 COCO_Haze_Val 和 COCO_Dark_Val 数据集上的比较，分别在 $COCO_Haze_Train\mathit{COCO\_Haze\_Train}$ 和 $COCO_Dark_Train\mathit{COCO\_Dark\_Train}$ 上训练。我们比较了一体化恢复方法 InstructIR [14]。我们的方法在所有评估指标上持续提升性能，在 mAP 上分别实现了 1.0 和 1.2 的提升。
在这里插入图片描述

5.3 评估与分析

计算复杂度评估。表3展示了参数（Params）和浮点运算次数（FLOPs）的比较，展示了我们框架的推理效率。
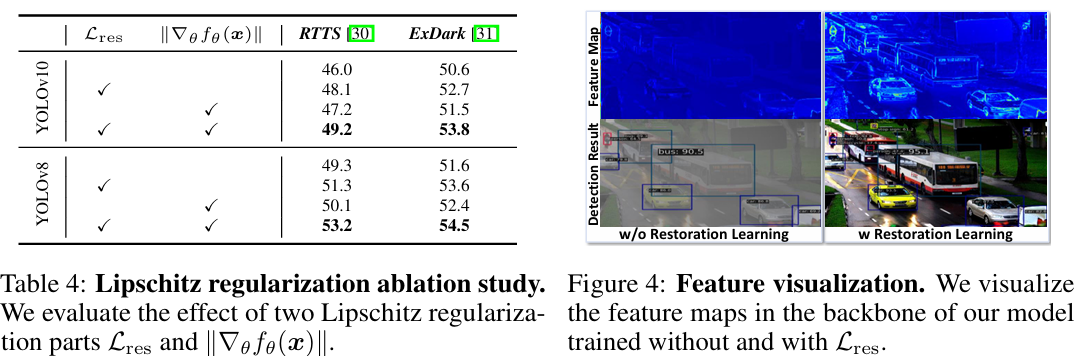
在这里插入图片描述

Lipschitz 正则化消融研究。我们评估了两个 Lipschitz 正则化部分（低 Lipschitz 恢复学习 $Lres\mathcal{L}_{\mathrm{res}}$ 和参数空间平滑 $∥∇θfθ~(x)∥\|\nabla_{\theta}\tilde{f_{\theta}}(\pmb{x})\|$ ）的影响。评估在 RTTS 和 ExDark 上进行，以衡量域外性能，如表4所示。在训练期间同时结合恢复学习和参数空间平滑，可以改善检测与恢复之间的协同作用，与基线方法相比，在 RTTS 上为 YOLOv10 和 YOLOv8 分别带来了 3.2 和 3.9 的 mAP 增益，在 ExDark 上分别带来了 3.2 和 2.9 的增益。

恢复学习分析。我们可视化了在有和没有恢复学习 $Lres\mathcal{L}_{\mathrm{res}}$ 的情况下训练的我们模型的主干特征，如图4所示。将恢复学习集成到检测器的特征学习中，有助于在主干中增强退化图像的特征，从而改善检测（例如，完整地检测到停车标志和摩托车）。

替代正则化消融研究。我们通过在 VOC_Haze_Train 上训练并在 RTTS 上进行域外评估，将我们的方法与两种替代正则化策略——谱范数正则化（SNR[22]）和通过 PGD[32] 进行的对抗训练——进行了比较。如表5所示，我们的方法在 RTTS 性能上达到了最佳，超过了 SNR 和 PGD。与全局约束权重的 SNR 不同，我们的方法惩罚 $∥∇θfθ~(x)∥\|\nabla_{\theta}\tilde{f_{\theta}}(\pmb{x})\|$ ，降低了输出对参数变化的敏感性，并实现了输入感知的平滑性。与基于 PGD 的对抗训练相比，后者需要生成扰动输入并增加训练成本，而我们的方法在没有对抗样本的情况下实现了隐式鲁棒性，从而实现了更稳定、更高效的训练，并且在干净输入上没有观察到性能下降。
在这里插入图片描述

架构变体消融研究。我们通过改变检测和恢复之间共享编码器的深度来进行消融实验，在 $VOC_Haze_Train\mathit{VOC\_Haze\_Train}$ 上训练并在 RTTS 上进行域外评估。如表6所示，较浅的共享（F1-F2）提供的正则化不足，而更深的共享（F1–F4）则引入了任务干扰，支持了我们选择共享前三个阶段（F1–F3）的设计。
在这里插入图片描述

正则化系数消融研究。我们通过扫描 $λ∈{0,5,10,20}\lambda \in \{0, 5, 10, 20\}$ 和 $λp∈{0,0.005,0.01,0.02}\lambda_{p} \in \{0, 0.005, 0.01, 0.02\}$ ，在 $VOC_Haze_Train\mathit{VOC\_Haze\_Train}$ 上训练并在 RTTS 上进行域外评估，对输入空间和参数空间的正则化强度进行了消融研究。如表7所示，我们的方法在一系列系数值下始终优于基线，性能波动很小，证明了对正则化强度选择的鲁棒性。
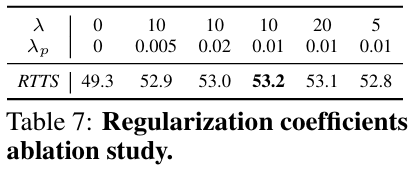
在这里插入图片描述

Lipschitz 连续性分析。我们在训练过程中分析了输入空间和参数空间中 Lipschitz 连续性的变化。具体来说，我们监控输入空间中雅可比范数的上界 $sup⁡x∈dom(f)∥∇xfθ(x)∥\sup_{\boldsymbol{x}\in \text{dom}(f)}\|\nabla_{\boldsymbol{x}}f_{\theta}(\boldsymbol{x})\|$ ，其中 $dom(f)\text{dom}(f)$ 代表来自 Pascal VOC 的输入图像域。此外，我们还跟踪参数空间中的梯度范数 $∥∇θfθ(x)∥\|\nabla_{\theta}f_{\theta}({\pmb x})\|$ 。如图5所示，与 ConvIR→YOLOv8 和 YOLOv8 相比，使用 $Lres\mathcal{L}_{\mathrm{res}}$ 训练的 LR-YOLOv8 在训练过程中降低了输入和参数空间中的 Lipschitz 常数。使用 $∥∇θfˉθ(x)∥\|\nabla_{\theta}\bar{f}_{\theta}({\pmb x})\|$ 进行训练进一步促进了输入和参数空间中的 Lipschitz 连续性。

在其他检测范式上的泛化能力。我们通过将其 LROD 集成到基于 Transformer 的检测器（RT-DETR [33]）和两阶段检测器（Faster R-CNN [34]）的共享主干中，进一步验证了 LROD 的泛化能力。所有模型均在 VOC_Haze_Train 上训练，并在合成的 VOC_Haze_Val 和真实世界的 RTTS 数据集上进行评估。如表8所示，LROD 在使用其他检测范式时始终优于其他方法，在 RTTS 上实现了 1.4 的 mAP 提升，支持了 LROD 作为一种即插即用正则化框架的有效性。
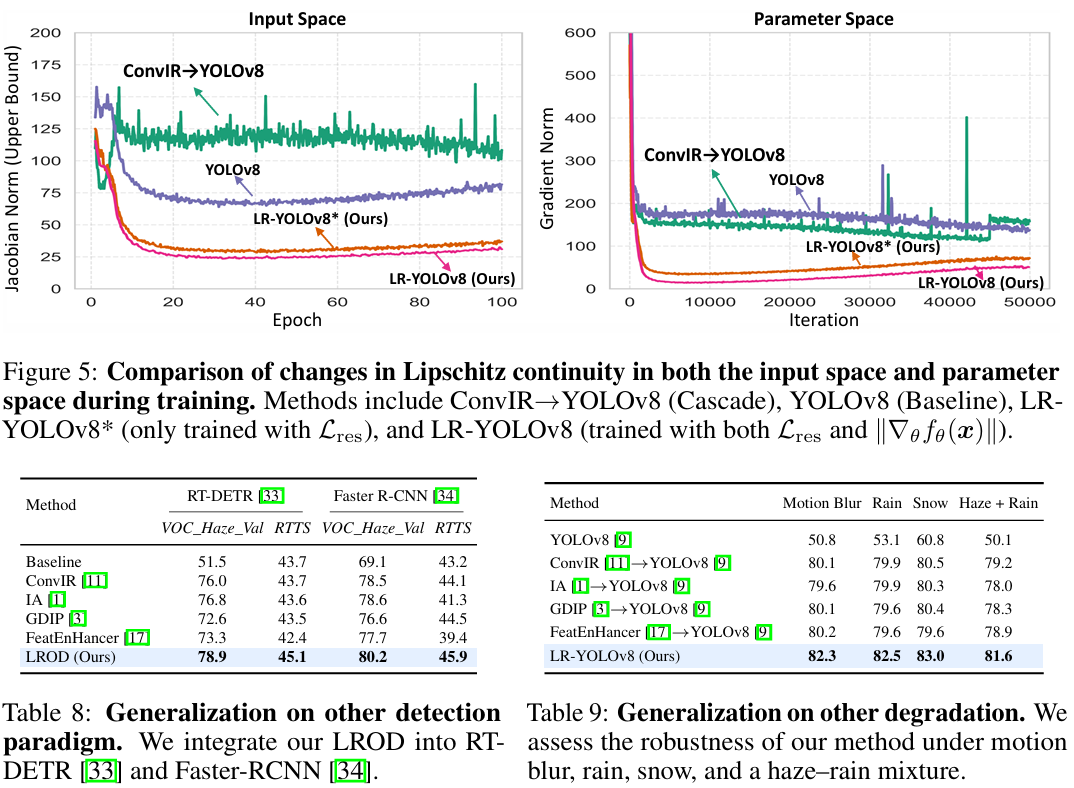
在这里插入图片描述
在其他退化类型上的泛化能力。我们通过构建每种退化的匹配训练/验证集并为每种设置重新训练所有方法，进一步评估了在其他恶劣条件（运动模糊、雨、雪和雾霾-雨混合）下的鲁棒性。如表9所示，我们的方法在所有情况下均持续优于现有方法，分别实现了 2.1、2.6、2.5 和 2.4 的 mAP 增益。这些结果凸显了我们的方法在各种退化类型下的通用性和鲁棒性。

6 结论

在本文中，我们通过输入和参数空间中的 Lipschitz 连续性视角，重新审视了在恶劣条件下图像恢复和目标检测的集成。我们的分析揭示了这两个任务之间 Lipschitz 连续性的固有不匹配在直接级联时会引入不稳定性。为了解决这个问题，我们提出了一个 Lipschitz 正则化框架，通过约束目标检测的 Lipschitz 连续性来协调这两个任务。这是通过低 Lipschitz 恢复学习在检测前平滑扰动，以及通过参数空间正则化在训练期间稳定梯度流来实现的。我们将这种方法实现为 Lipschitz 正则化 YOLO（LR-YOLO），它可以以最小的开销扩展到现有的 YOLO 检测器。在雾霾和低光基准上的大量实验表明，我们的方法提高了检测的稳定性和优化的平滑度，从而在具有挑战性的环境中实现了更鲁棒的性能。

局限性与未来方向。虽然我们的方法已在多种恶劣条件下（包括雾霾、雨、雪、低光和混合天气）得到验证，但目前的一个局限是假设每个输入只包含一种类型的退化。一个有价值的方向是将我们的框架扩展到处理受多种并发退化影响的输入。另一个有前景的方向是将我们的 Lipschitz 连续性分析扩展到伪装目标检测（CoD [35, 36]），因为 CoD 涉及检测具有模糊、低对比度边界的物体，在恶劣条件下给级联系统带来了类似的挑战。

致谢

本工作部分得到了国家自然科学基金（NSFC）项目（编号 62376292, U21A20470）、广东省基础与应用基础研究基金（编号 2024A1515010208）以及广州市科技计划项目（编号 2025A04J5465, 2024A04J6365）的支持。

附录

A 详细证明

备注3（通过低 Lipschitz 恢复进行 Lipschitz 正则化）。令： $fθb,θd=fθd∘fθbf_{\theta_{b},\theta_{d}} = f_{\theta_{d}} \circ f_{\theta_{b}}$ 表示目标检测模型，其中 $fθb(⋅;θb)f_{\theta_{b}}(\cdot;\theta_{b})$ 是由 $θb\theta_{b}$ 参数化的主干网络， $fθd(⋅;θd)f_{\theta_{d}}(\cdot;\theta_{d})$ 是由 $θd\theta_{d}$ 参数化的检测头。类似地，令： $gθb,θr=fθr∘fθbg_{\theta_{b},\theta_{r}} = f_{\theta_{r}} \circ f_{\theta_{b}}$ 表示图像恢复模型，其中 $fθr(⋅;θr)f_{\theta_{r}}(\cdot;\theta_{r})$ 是由 $θr\theta_{r}$ 参数化的恢复头，共享相同的主干 $fθbf_{\theta_{b}}$ 。给定检测损失和恢复损失的加权组合：
$L(θb,θd,θr)=Ldet(fθb,θd)+λ⋅Lres(gθb,θr),λ>0\mathcal{L}(\theta_{b},\theta_{d},\theta_{r})=\mathcal{L}_{\mathrm{det}}(f_{\theta_{b},\theta_{d}})+\lambda\cdot\mathcal{L}_{\mathrm{res}}(\boldsymbol{g}_{\theta_{b},\theta_{r}}),\quad\lambda>0$
令 $Lip⁡(fθb):=sup⁡x∥Jfθb(x)∥\operatorname{Lip}(f_{\theta_{b}}):=\sup_{\pmb{x}}\|J_{f_{\theta_{b}}}(\pmb{x})\|$ 为由雅可比范数定义的 $fθbf_{\theta_{b}}$ 的 Lipschitz 常数。如果：

$Lres\mathcal{L}_{\mathrm{res}}$ 是 Lipschitz 连续的，并且 $∥∇θbLres(gθb,θr)∥≤G\|\nabla_{\theta_{b}}\mathcal{L}_{\mathrm{res}}(\boldsymbol{g}_{\theta_{b},\theta_{r}})\| \leq G$ ，其中 $\|\nabla_{\theta_{b}}\mathcal{L}_{\mathrm{det}}(f_{\theta_{b},\theta_{d}})\|$ ；
存在一个训练样本 $x⋆\boldsymbol{x}^{\star}$ 和 $γ>0\gamma>0$ ，使得： $⟨∇θb∥Jfθb(x⋆)∥,∇θbLres(gθb,θr)⟩≥γ\left\langle \nabla_{\theta_{b}}\|J_{f_{\theta_{b}}}(\boldsymbol{x}^{\star})\|, \nabla_{\theta_{b}}\mathcal{L}_{\mathrm{res}}(\boldsymbol{g}_{\theta_{b},\theta_{r}})\right\rangle \geq \gamma$ ，

那么在连续时间梯度下降 $θb(t+1)←θb(t)−μ⋅∇θbL(θb,θd,θr){\theta_{b}}^{(t+1)}\leftarrow{\theta_{b}}^{(t)}-\mu\cdot\nabla_{\theta_{b}}\mathcal{L}(\theta_{b},\theta_{d},\theta_{r})$ （ $μ\mu$ 表示学习率）下，Lipschitz 常数的演化满足：
$ddt[Lip(fθb)]≤−λ⋅γ+ξ(t)\frac{d}{d t}\left[\mathrm{Lip}(f_{\theta_{b}})\right]\leq-\lambda\cdot\gamma+\xi(t)$
其中 $ξ(t):=⟨∇θb∥Jfθb(x⋆)∥,∇θbLdet(fθb,θd)⟩\xi(t) := \left\langle \nabla_{\theta_{b}}\|J_{f_{\theta_{b}}}(\pmb{x}^{\star})\|, \nabla_{\theta_{b}}\mathcal{L}_{\mathrm{det}}(f_{\theta_{b},\theta_{d}})\right\rangle$ 是由检测损失引起的无约束变化， $γ\gamma$ 是通过恢复任务实现的正则化。

这表明，通过共享检测器的主干，将图像恢复任务直接集成到检测器的特征学习中，有助于在训练期间抑制模型对输入扰动的敏感性，有效地起到 Lipschitz 正则化的作用。

证明。根据 [25] 中的定理1， $fθbf_{\theta_{b}}$ 的 Lipschitz 常数为：
$Lip⁡(fθb)=sup⁡x∥Jfθb(x)∥\operatorname{Lip}(f_{\theta_{b}})=\sup_{\pmb x}\|J_{f_{\theta_{b}}}(\pmb x)\|$
令 $x⋆\boldsymbol{x}^{\star}$ 为达到或近似该上确界的输入。那么，在连续时间梯度下降过程中：
$ddt[Lip(fθb)]=ddt∥Jfθb(x⋆)∥=⟨∇θ∥Jfθb(x⋆)∥2,−∇θbL(θb,θd,θr)⟩\frac{d}{d t}\left[\mathrm{Lip}(f_{\theta_{b}})\right]=\frac{d}{d t}\|J_{f_{\theta_{b}}}(\boldsymbol{x}^{\star})\|=\left\langle \nabla_{\theta}\|J_{f_{\theta_{b}}}(\boldsymbol{x}^{\star})\|_{2}, -\nabla_{\theta_{b}}\mathcal{L}(\theta_{b},\theta_{d},\theta_{r})\right\rangle$
代入联合损失：
$ddt[Lip(fθb)]=−⟨∇θb∥Jfθb(x⋆)∥,∇θbLdet(fθb,θd)+λ⋅∇θbLres(gθb,θr)⟩\frac{d}{d t}\left[\mathrm{Lip}(f_{\theta_{b}})\right]=-\left\langle \nabla_{\theta_{b}}\|J_{f_{\theta_{b}}}(\boldsymbol{x}^{\star})\|, \nabla_{\theta_{b}}\mathcal{L}_{\mathrm{det}}(f_{\theta_{b},\theta_{d}})+\lambda\cdot\nabla_{\theta_{b}}\mathcal{L}_{\mathrm{res}}(\boldsymbol{g}_{\theta_{b},\theta_{r}})\right\rangle$
分解为两个部分：
$ddt[Lip⁡(fθb)]=−⟨∇θb∥Jfθb(x⋆)∥,∇θbLdet⁡(fθb,θd)⟩−λ⋅⟨∇θb∥Jfθb(x⋆)∥,∇θbLres⁡(gθb,θr)⟩\frac{d}{d t}\left[\operatorname{Lip}(f_{\theta_{b}})\right]=-\left\langle \nabla_{\theta_{b}}\|J_{f_{\theta_{b}}}(\mathbf{x}^{\star})\|, \nabla_{\theta_{b}}\mathcal{L}_{\operatorname*{det}}(f_{\theta_{b},\theta_{d}})\right\rangle-\lambda\cdot\left\langle \nabla_{\theta_{b}}\|J_{f_{\theta_{b}}}(\mathbf{x}^{\star})\|, \nabla_{\theta_{b}}\mathcal{L}_{\operatorname{res}}(g_{\theta_{b},\theta_{r}})\right\rangle$
根据假设2，第二项有下界：
$⟨∇θ∥Jfθ(x⋆)∥2,∇θLres(gθb,θr)⟩≥γ\left\langle \nabla_{\theta}\|J_{f_{\theta}}(\boldsymbol{x}^{\star})\|_{2}, \nabla_{\theta}\mathcal{L}_{\mathrm{res}}(\boldsymbol{g}_{\theta_{b},\theta_{r}})\right\rangle\geq\gamma$
将第一项定义为 $ξ(t)\xi(t)$ ，则：
$ddt[Lip(fθ)]≤−λγ+ξ(t)\frac{d}{d t}\left[\mathrm{Lip}(f_{\theta})\right]\leq-\lambda\gamma+\xi(t)$
证明完毕。
□

图6：Lipschitz 正则化 YOLO（LR-YOLO）的整体架构。

B 详细模型

为了高效且有效地协调图像恢复和目标检测，我们将图像恢复学习集成到目标检测主干的特征提取过程中。这种集成在训练期间隐式地强制执行 Lipschitz 连续性，从而在不同退化强度下增强检测器的稳定性。如图6所示，我们通过从主干的前三个阶段提取低级特征来扩展现有的 YOLO 检测器，而不修改原始网络架构。然后，这些特征由一个轻量级的、对恢复感知的模块进行处理，该模块重建输入图像的干净版本，并促进检测网络内更平滑、更稳定表示的学习。

YOLO 检测器。YOLO 架构是一个单阶段目标检测框架，它在单次前向传递中执行检测，实现了高效率和速度。它由三个主要组件组成，即：主干（Backbone），从输入图像中提取视觉特征；颈部（Neck），聚合多尺度特征以增强表示；头部（Head），预测边界框、类别分数和目标性。由于其高计算效率和易于在边缘设备上部署，YOLO 被广泛应用于实时检测应用。

低 Lipschitz 恢复模块。为了改善目标检测在恶劣成像条件下的稳定性，我们在 YOLO 框架中引入了一个对恢复感知的模块。如图6所示，我们从 YOLO 主干的前三个阶段（记为 F1、F2 和 F3）提取低级特征，这些特征保留了图像恢复所必需的丰富空间和纹理信息。受 YOLO 颈部和头部设计的启发，这些特征通过一个由多个跨阶段局部层（CSPLayer）组成的特定于恢复的颈部和解码器。该模块采用密集连接的架构，有助于多尺度特征融合，这对于有效的恢复学习至关重要。通过逐步优化低级表示，该模块重建了受视觉退化影响较小的输入图像的恢复版本。这个对恢复感知的模块不仅由于恢复固有的平滑性在训练期间有助于 YOLO 检测器的稳定性，还增强了检测器用于下游检测任务的低级特征。

C 详细数据集

数据集涵盖两种具有挑战性的条件：雾天和低光环境。对于这两种设置，我们使用真实世界数据集进行域外评估，并基于 PASCAL VOC [26] 构建合成的训练/验证集，遵循 IA-YOLO [1]、ReForDe [2] 和 Vat [5] 的做法：

训练和验证数据：我们通过选择包含相关物体类别的 PASCAL VOC [26] 图像来构建合成数据集：
- VOC_Haze_Train 和 VOC_Haze_Val 分别包含 8,111 和 2,734 张图像。雾霾在训练期间使用大气散射模型在线合成， $β∈[0.5,1.5]\beta\in[0.5,1.5]$ ，而验证图像则离线合成一次以保证可重现性。
- VOC_Dark_Train 和 VOC_Dark_Val 分别包含 12,334 和 3,760 张图像。低光在训练期间通过伽马校正在线模拟，在验证时离线进行， $γ∈[1.5,5]\gamma\in[1.5,5]$ 。
真实世界测试数据。我们采用两个基准数据集进行域外评估：
- RTTS [30]：包含 4,322 张真实世界雾霾图像，标注了5个物体类别，即：人、汽车、公共汽车、自行车和摩托车。
- ExDark [31]：包含 2,563 张真实世界低光图像，标注了10个类别，即：人、汽车、公共汽车、自行车、摩托车、船、瓶子、椅子、狗和猫。
  上述数据集中每个类别的物体标注数量如表10和表11所示。

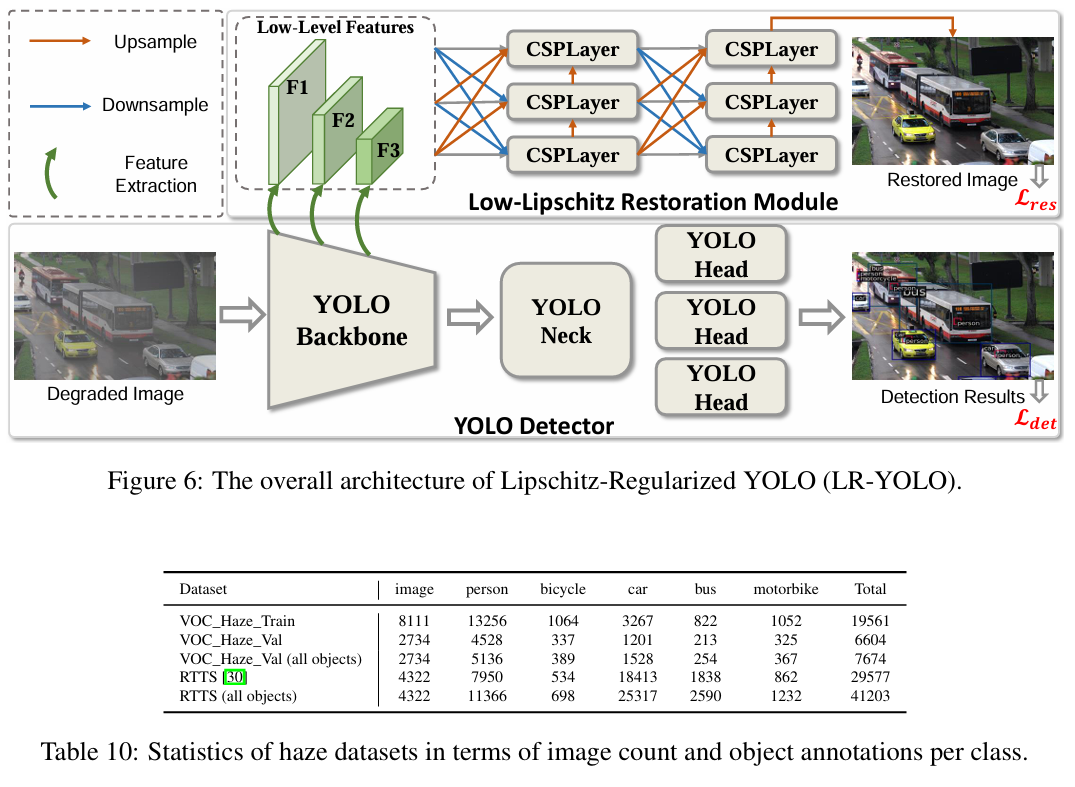
D 详细检测结果

我们在 VOC_Haze_Val 和 RTTS 数据集上报告了每个类别的平均精度，如表12所示，在 VOC_Dark_Val 和 ExDark 数据集上的结果如表14所示。
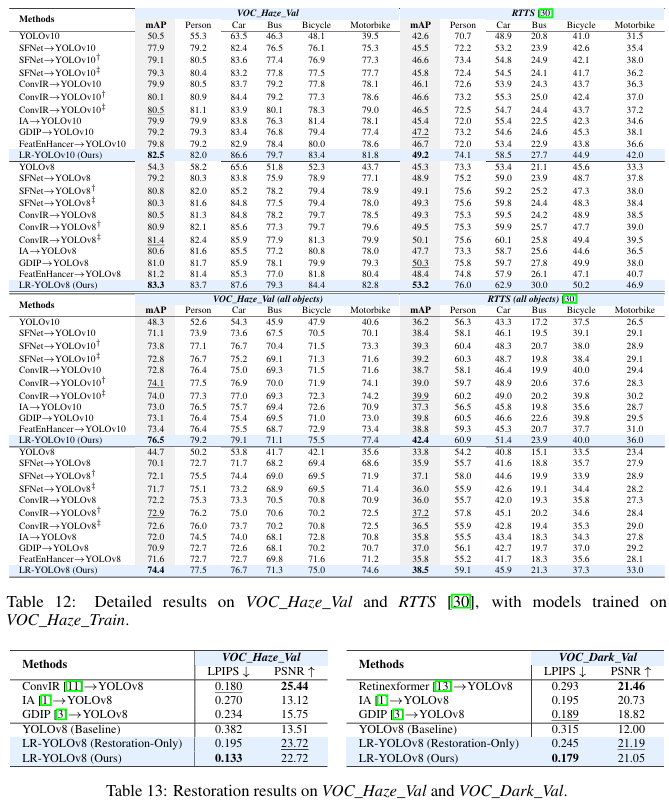
在这里插入图片描述

E1 图像恢复评估

我们使用峰值信噪比（PSNR）评估像素级保真度和使用学习感知图像块相似度（LPIPS）[37]评估感知相似度，来评估我们的 LR-YOLO 在雾霾和低光条件下的恢复性能。表13展示了在 VOC_Haze_Val 和 VOC_Dark_Val 上的恢复结果。我们将我们的方法与图像去雾技术 ConvIR [11]、低光增强方法 Retinexformer [13] 以及图像自适应方法 IA [1] 和 GDIP [3] 进行了比较。我们的完整模型在 VOC_Haze_Val 和 VOC_Dark_Val 上都取得了最佳的 LPIPS 分数和有竞争力的 PSNR，优于基线 YOLOv8 和图像自适应管道。此外，我们仅恢复的变体（LR-YOLOv8 (仅恢复)，仅使用恢复学习进行训练）在重建保真度上取得了平衡的改进。
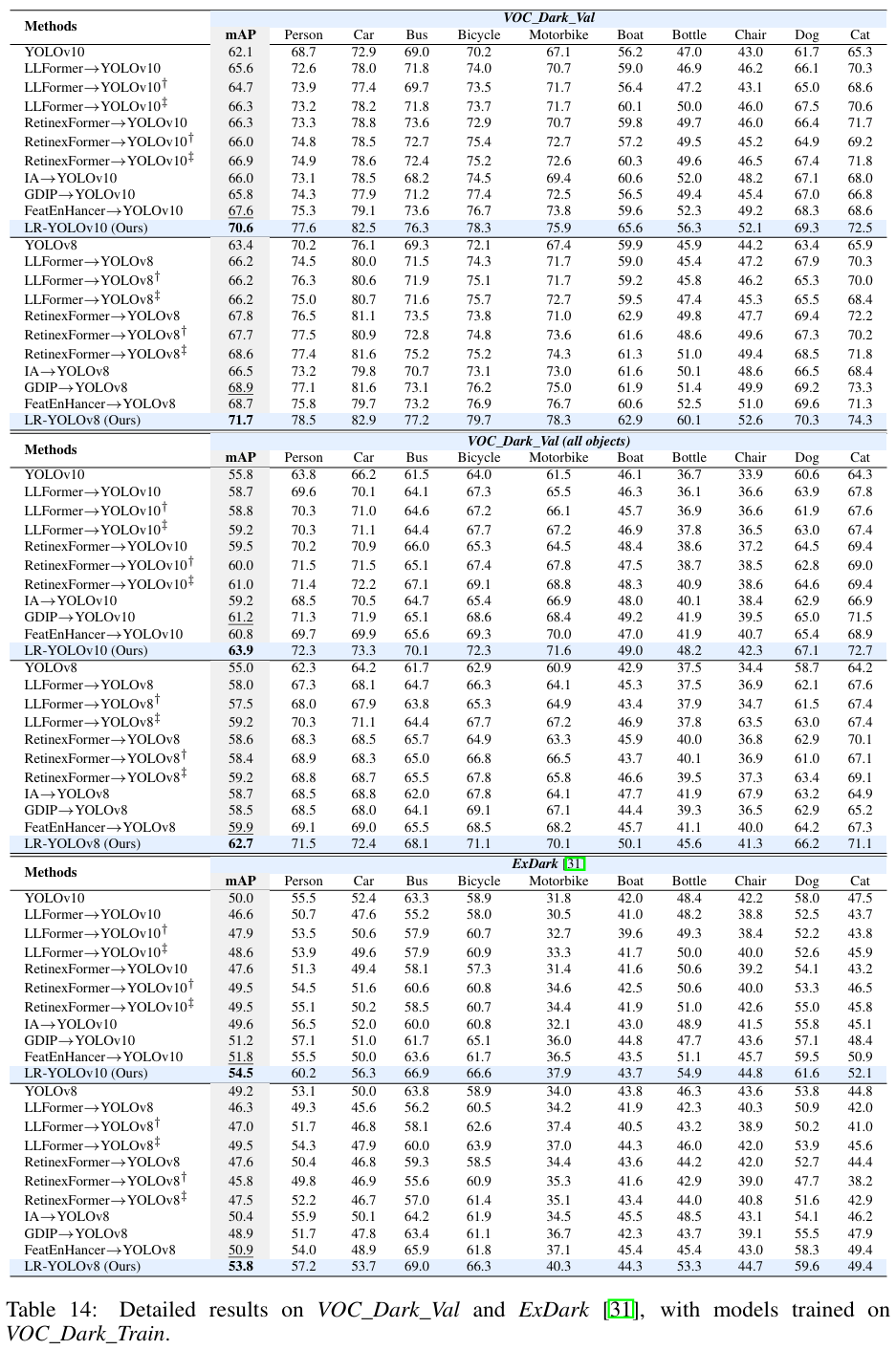
在这里插入图片描述

F 定性比较

图2(a)说明了级联方法的检测器特征对微小的雾霾密度变化 $Δx\Delta x$ 高度敏感，而我们的 Lipschitz 正则化框架保持了稳定性。检测结果稳定性的定性比较在图7中展示。当两个具有轻微雾霾密度变化 $Δx\Delta x$ 的雾霾输入 $x$ 和 $x+Δxx+\Delta x$ 被送入模型时，级联方法 $(ConvIR→YOLOv8)\mathrm{(ConvIR \rightarrow YOLOv8)}$ 的检测结果表现出显著的不稳定性，即使这些雾霾可以通过图像去雾方法缓解。例如，一辆汽车在一个案例中被检测到，而在另一个案例中没有被检测到，一个人突然未被检测到。这突显了级联框架固有的不稳定性。图8（雾霾条件）和图9（低光条件）中的视觉示例定性地说明了我们的方法在提高检测准确性和感知质量方面的有效性，从而增强了人类对检测结果的信任。
在这里插入图片描述

G 更广泛的影响

在恶劣天气和低光环境下改进目标检测，对自动驾驶、交通监控和搜救任务等安全关键型应用具有重要意义。特别是，自动驾驶汽车经常在不可预测的环境条件下运行。在雾天或夜间场景中无法准确检测行人、车辆或障碍物，可能会导致危及生命的后果。我们的方法旨在通过联合增强视觉清晰度和检测准确性来填补这一空白，为现有感知管道提供潜在的安全升级。

然而，这项研究也涉及更广泛的考量。首先，部署先进的视觉检测系统可能会增强城市和农村地区的监控能力。虽然这可能会提高公共安全，但也引发了对隐私的担忧以及被威权实体滥用的潜在风险。

其次，应评估模型在不同人口和地理环境下的性能。不同地区的恶劣天气状况可能存在显著差异（例如，烟雾与海雾），确保模型在不同环境和社区中公平地泛化，对于避免有偏见的部署结果至关重要。

最后，我们承认在低能见度环境中改进的检测能力可能会被用于军事或安全应用。尽管所提出的方法旨在用于民用安全和交通改善，但存在双重用途的风险。

查看全文

http://www.dtcms.com/a/564930.html