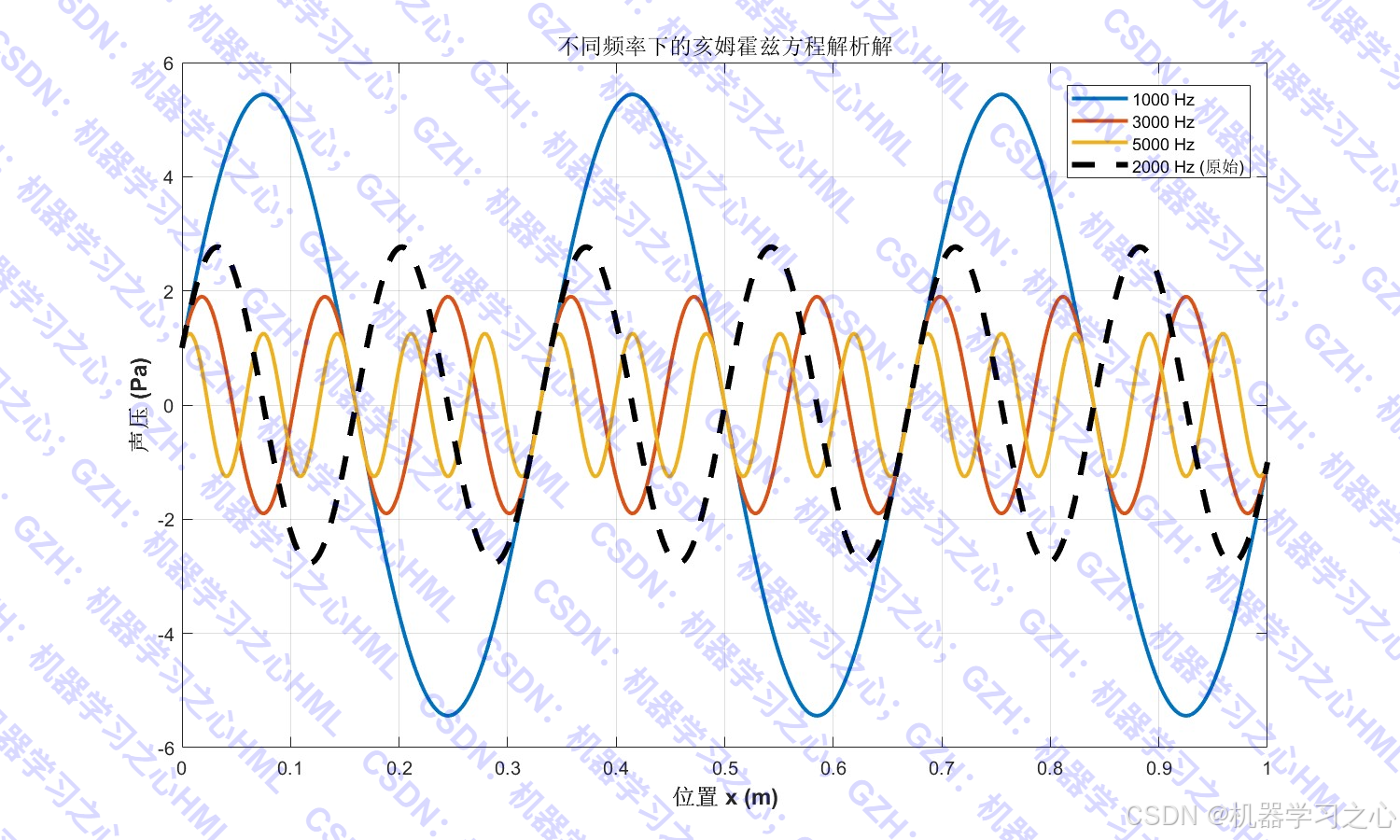
PINN求解一维亥姆霍兹方程，以声学问题为例，使用L-BFGS优化器，将传统物理建模与现代深度学习相结合，为解决科学计算问题提供了新的范式，MATLAB代码

代码主要功能

基于物理信息神经网络（PINN）求解一维亥姆霍兹方程的完整MATLAB实现。亥姆霍兹方程是波动方程的频域形式，广泛应用于声学、电磁学等领域。

算法步骤

1. 数据准备阶段

   • 定义物理参数（频率、声速、波数）
   • 设置边界条件
   • 使用Sobol序列生成内部配置点

2. 神经网络构建

   • 构建多层全连接神经网络
   • 使用He初始化方法初始化权重
   • 零初始化偏置项

3. 训练过程

   • 定义物理约束的损失函数
   • 使用fmincon优化器进行训练
   • 监控训练进度和收敛情况

4. 结果验证

   • 在测试集上评估模型精度
   • 比较预测解与解析解
   • 计算相对误差

5. 可视化分析

   • 多维度结果展示
   • 误差分析
   • 不同参数对比

技术路线

核心技术：物理信息神经网络（PINN）

• 传统神经网络：仅依赖数据驱动
• PINN：将物理定律（偏微分方程）作为约束融入损失函数

网络架构特点

• 激活函数：使用sin函数作为激活函数，适合周期性问题
• 自动微分：利用MATLAB的dlgradient计算高阶导数
• 试函数构造：通过基函数自动满足边界条件

公式原理

一维亥姆霍兹方程

$$d^{2}u/d{x}^2+k^{2}u=0$$
其中：

• u是声压场
• k = 2πf/c是波数
• f是频率，c是声速

边界条件

$$u(0)=1,u(1)=-1$$

试函数构造

为避免显式处理边界条件，构造试函数：

$$G(x)={\phi }_1(x)u_{01}+{\phi }_2(x)u_{02}+{\phi }_{e}qv(x)U(x)$$
其中：

• φ₁(x) = 1-x，φ₂(x) = x（线性基函数）
• φ_eqv(x) = x(1-x)（确保边界处为零）
• U(x)是神经网络输出

损失函数

基于物理残差的L2范数：

$$loss=||d^{2}G/d{x}^2+k^{2}G|{|}^2$$

参数设定

物理参数

freq = 2000;     % 频率：2000 Hz
c0 = 340;        % 声速：340 m/s
k = 2*pi*freq/c0; % 波数计算

边界条件

x0BC1 = 0; u0BC1 = 1;   % 左边界
x0BC2 = 1; u0BC2 = -1;  % 右边界

神经网络参数

numLayers = 5;          % 网络层数：5
numNeurons = 90;        % 每层神经元：90
numInternalCollocationPoints = 14000; % 训练点数

优化参数

MaxIterations = 1000;           % 最大迭代次数
OptimalityTolerance = 1e-3;     % 收敛容差
HessianApproximation = "lbfgs"; % L-BFGS优化算法

运行环境要求

必需软件

• MATLAB (推荐R2024b或更新版本)
• 深度学习工具箱 (Deep Learning Toolbox)
• 优化工具箱 (Optimization Toolbox)

应用场景

主要应用领域

1. 声学工程

   • 管道声传播分析
   • 房间声学模拟
   • 噪声控制设计

2. 电磁学

   • 波导传输分析
   • 天线设计优化
   • 电磁兼容分析

3. 结构力学

   • 振动模态分析
   • 弹性波传播

技术优势

• 无网格方法：避免传统FEM的网格生成
• 数据高效：仅需边界条件和方程，无需大量训练数据
• 物理一致性：解自动满足物理定律
• 连续解：在整个域内提供连续可微的解

适用问题特征

• 已知控制方程但边界复杂的问题
• 传统数值方法难以处理的高维问题
• 需要快速参数化分析的设计问题

完整代码私信回复PINN求解一维亥姆霍兹方程，以声学问题为例，使用L-BFGS优化器，MATLAB代码