当前位置：首页 > news >正文

基于无六环H校验矩阵和归一化偏移minsum算法的LDPC编译码matlab性能仿真

news 2025/11/4 8:03:04

1.引言

2.算法仿真效果演示

3.数据集格式或算法参数简介

4.算法涉及理论知识概要

4.1无六环H校验矩阵构造

4.2 归一化偏移min-sum译码算法

5.完整算法代码文件获得

1.引言

LDPC码（低密度奇偶校验码）作为一类性能接近香农极限的纠错编码，其编译码性能与H校验矩阵的构造及译码算法的选择密切相关。本课题将实现于“无六环H校验矩阵构造”与“归一化偏移min-sum译码算法” 的组合方案。

2.算法仿真效果演示

软件运行版本：

matlab2024b

仿真结果如下（仿真操作步骤可参考程序配套的操作视频，完整代码运行后无水印）

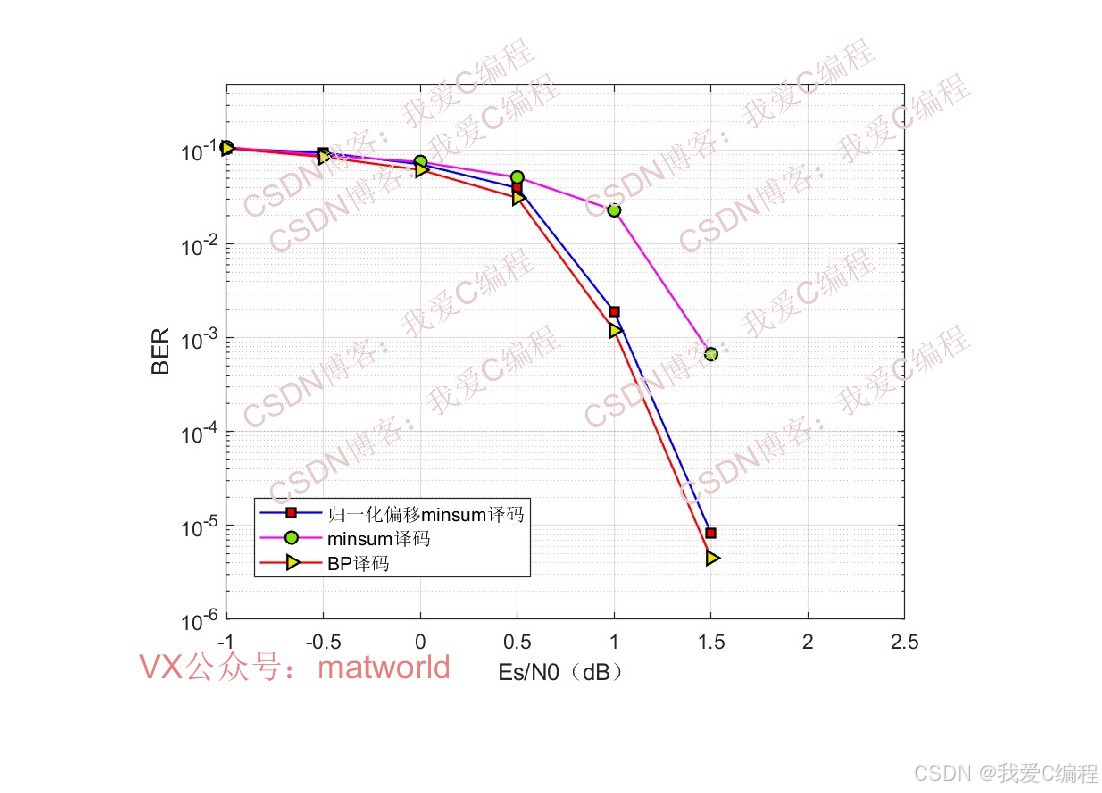
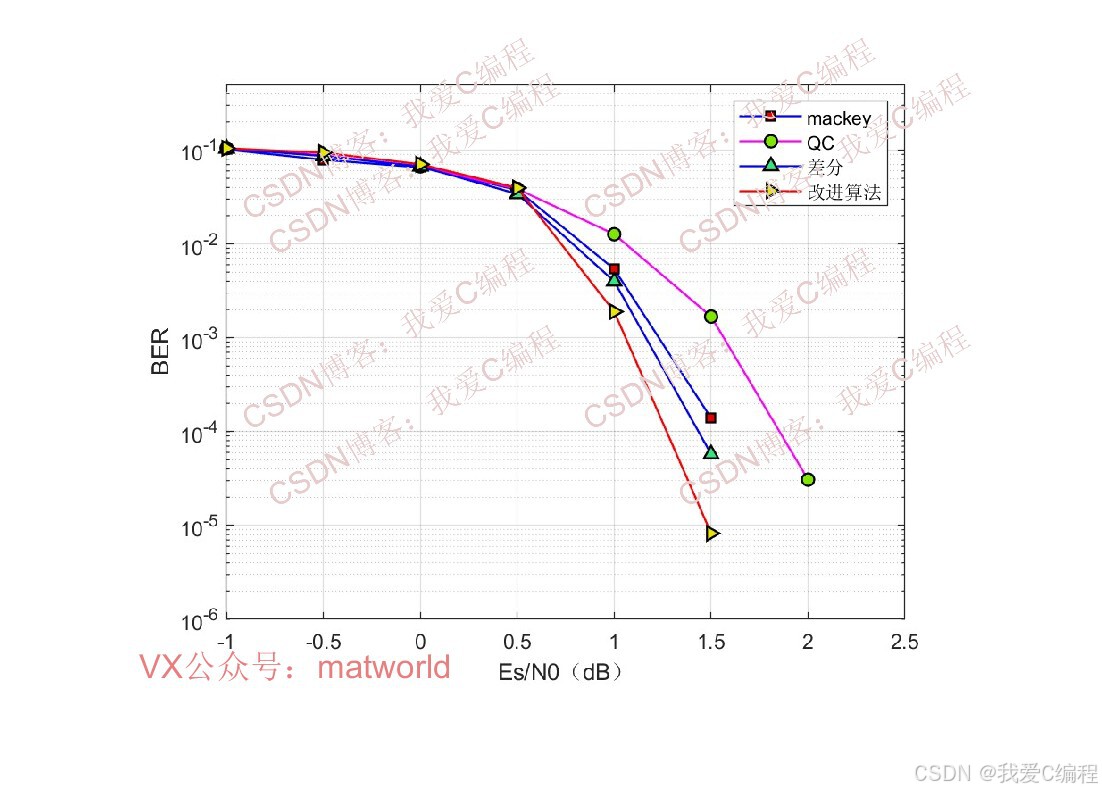
3.数据集格式或算法参数简介

%%
n           = 3;
m           = 6;
p           = 200;
N           = m*p;
M           = n*p;
EsN0        =-1:0.5:1.5;
R           = n/m;
k           = R*log2(2);
EbN0        = EsN0/k;
Max_iter    = 10; 
H1          = func_dys(n,m,p);
% H2          = func_dys(n,m,2*p);
NUMS        = [500,400,300,200,100,50];
014_034m

4.算法涉及理论知识概要

4.1无六环H校验矩阵构造

H校验矩阵是LDPC码的核心，其环结构直接影响编码性能。环是指H矩阵中由非零元素构成的闭合路径，四环、六环等短环会导致校验信息相关性增强，降低译码准确性。传统构造算法（如 Mackey算法）虽能实现无四环结构，但性能仍受限于潜在的六环影响，因此本文提出无六环H矩阵的改进构造方案。

四环是H矩阵中最短的有害环，其数学表达为特定非零元素的位置关系满足：(Pj - Pₖ) + (Pₘ - Pₙ) ≡ 0 mod P（P为循环置换矩阵的尺寸）。构造时需通过大衍数列选数，确保所有满足该等式的非零元素组合均被排除，从根源上避免四环形成。

六环结构更为复杂，共存在六种典型拓扑形态，其通用约束可表示为： ∀(i,j,l,m,p,q) ∈ 矩阵索引集合，满足特定非零元素位置关系的组合需满足： f (i+5j)×i² - f (l+5m)×l² + f (p+5q)×p² ≡ C mod P（C为非零常数）通过该约束，确保H矩阵中不存在任何形式的六环闭合路径。

4.2 归一化偏移min-sum译码算法

基于传统min-sum算法的框架，融合归一化min-sum和偏移min-sum的核心优势：通过归一化系数调整校验节点更新的幅值，通过偏移量补偿min-sum算法的固有近似误差，最终实现“低复杂度+高性能”的译码效果。

校验节点更新的归一化改进引入归一化系数α，对校验节点消息进行幅值校准，修正传统minsum算法的近似误差：

uₘₗ = α × f (Vₙₘ) × [L'(m)/L (m)]

其中f (x) = log [cosh (x/2)]，近似等价于tanh (x/2)的对数形式；L(m)为校验节点m的度数，L'(m)为有效连接度数；sign (vₘₗ)为变量节点消息的符号函数，用于保留校验信息的极性。

偏移量引入与最终更新公式在归一化基础上加入偏移量σ，进一步补偿算法偏差，最终校验节点更新公式为：

uₘₗ = α × f (Vₙₘ) × [L'(m)/L (m)]-σ

核心改进在于通过α和σ的联合优化，在不改变算法迭代结构的前提下，提升消息传递的准确性。

基于无六环H校验矩阵和归一化偏移min-sum算法的LDPC编译码系统，通过矩阵构造与算法优化的双重改进，实现了性能与复杂度的最优平衡。无六环H矩阵从编码根源上抑制了短环影响，归一化偏移min-sum算法则在译码端高效恢复码字信息，两者协同作用，使LDPC码在保持稀疏性和低复杂度的同时，性能接近理论极限，为高速、高可靠通信系统提供了可行的技术方案。