Matlab模拟对流方程迎风格式验证
今天上计算机模拟课程,在课上要求利用matlab对“对流方程”的迎风格式进行验证,然后现在记录一下学习心得。
1.对流方程的简介
1.1 基本概念
对流是指流体中某一物质的传输伴随着流体的整体流动。例如,空气中的热量随着空气流动而传播,水流中的污染物被带到不同的位置。对流方程用来描述这一过程,通常涉及流体的速度、物质的浓度或温度等变量。
对流方程的标准形式为:
其中:
表示物理量(如温度、污染物浓度等)随时间 t和位置 x的变化。
是流体的速度(通常是向量形式);
表示物理量随空间的变化;
-
是物理量随时间的变化速率。
这个方程可以理解为一个量 随着速度
在空间中移动,但自身值保持不变。实际上也是如此,对流方程来源于物质守恒的基本原理,其核心思想是一个物理量随某一速度沿空间方向移动,量本身不变。
1.2. 对流方程的物理意义
- 对流方程描述了物理量在流体中的“传输”过程。这里,v是流体的速度,它影响物理量的迁移速率。具体来说,方程的第一项
描述物理量随时间的变化,第二项
描述物理量因流体运动而引起的空间变化。
- 对流方程的解决定了物理量在不同时间和空间的位置。例如,假设你把某种物质放入流动的水中,随着时间的推移,这种物质会随着水流扩散。对流方程能够帮助我们预测这种物质随时间和空间的分布情况。
1.3 迎风格式
迎风格式(Upwind Scheme)是求解偏微分方程中常用的数值离散方法,其根据物质传播的方向(例如流速 c>0 向右)选取前一个时间步上的“上风”点。如果流动方向为正,就用左侧点估计导数;如果方向为负,就用右侧点,就是选取前一时刻的点。
一维显式迎风格式(FTBS,First-order Upwind)公式:
化简:
其中表示节拍,
表示空间位置。
特点:
一阶精度(空间一阶,时间一阶)
稳定性好,只要满足 CFL 条件
。
数值黏性大,会导致波形变平、失真。
2.实例仿真
2.1初始条件和边界条件
初始条件决定了在某一时刻(通常是 t=0)系统的状态,u(x,0)=f(x)表示在时刻 t=0 时,物理量 u 在空间各点的初始分布。如果没有初始条件,方程会缺乏起始时刻的物理背景,因此无法唯一地确定物理量在时间上的演化。
边界条件决定了系统在空间边界处的行为。空间的边界是实际系统的物理限制,方程的解在这些边界上的行为是通过边界条件来设定的。没有边界条件,方程在空间域的解会存在无穷多种可能性。常见类型边界类型有:
Dirichlet 边界条件:指定边界处物理量的值,例如:
这表示在空间的两端(例如 x=0x=0 和 x=Lx=L)的物理量随时间变化。
- Neumann 边界条件:指定边界处物理量的导数(例如梯度),通常与流动或流量相关:
混合边界条件:同时使用 Dirichlet 和 Neumann 边界条件的组合。
2.2代码
- 正弦波
在空间中传播
- 初始条件为
- 边界条件:u(1:100) = 0;u(Nx-50:Nx)=0
% 设置参数 L = 12; % 空间域长度 T = 4; % 总时间 Nx =1000; % 空间网格数 Nt = 400; % 时间步数 v = 0.7; % 流速 dx = L / Nx; % 空间步长 dt = T / Nt; % 时间步长 %稳定性 e = dx / abs(v) - dt;if e >= 0disp("稳定"); elsedisp("不稳定"); end% 初始条件(提高频率的正弦波) x = linspace(0, L, Nx); u0 = sin(2*pi*x / L*(25)); % 原来是2*pi,改为4*pi使波峰变多 波长:l =2*pi /(2*pi/L)% 数值解 u = u0;u(Nx-800:Nx)=0;% 创建一个GIF文件 filename = 'wave_animation.gif'; % GIF文件名 % 迎风格式求解 for t = 1:Nt % 使用迎风格式更新ufor i = 2:Nxu(i) = u(i) - v*dt/dx * (u(i) - u(i-1));end% 边界条件:Dirichlet 条件u(1:100) = 0;u(Nx-50:Nx)=0;% 可视化plot(x, u, 'LineWidth', 2);axis([0 L -1.5 1.5 ]); % 空间域显示扩大到 L+5,右边多一些空白title(['Time = ', num2str(t*dt)]);xlabel('x');ylabel('u(x,t)');drawnow;% 捕捉当前帧frame = getframe(gcf); % 获取当前帧% 将当前帧转换为图像[A, map] = rgb2ind(frame.cdata, 256, 'nodither'); % 对于GIF的第一帧,直接创建GIF文件if t == 1imwrite(A, map, filename, 'gif', 'LoopCount', inf, 'DelayTime', 0.05);else% 从第二帧开始,将其附加到GIF文件imwrite(A, map, filename, 'gif', 'WriteMode', 'append', 'DelayTime', 0.05);end end结果如下图所示:
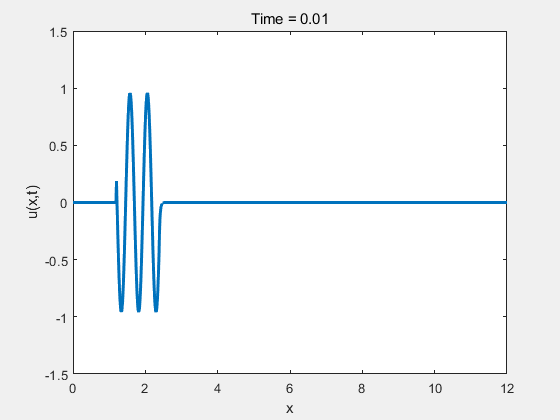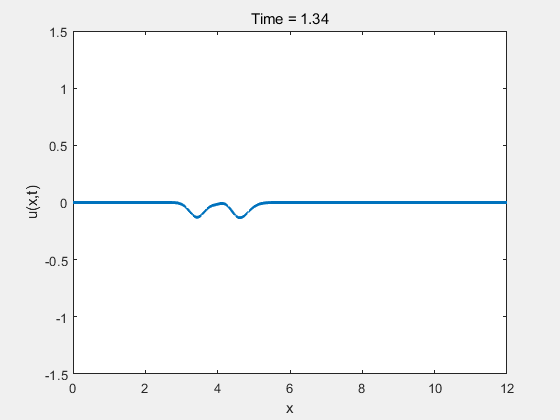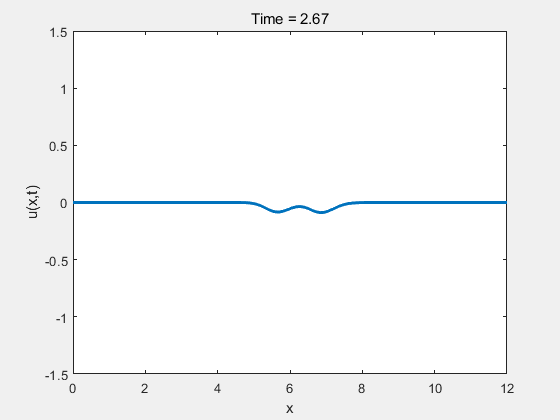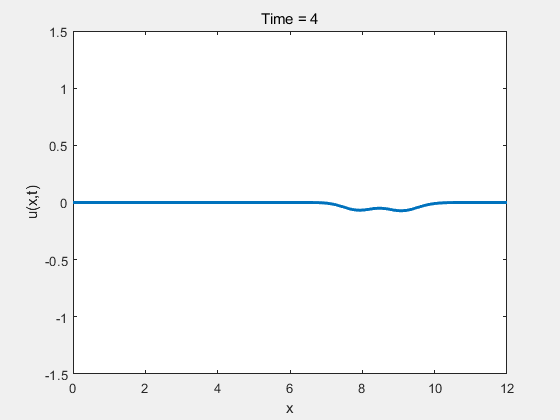
从图1可以看出,波形持续向前传播,且在传播过程中逐渐衰减。
这节课主要收获的是理解了网格的意义,将空间划分为不同的节点,然后在节拍中,不断向前传播。但是有点奇怪的是u最后衰减为0,和之前理解的不太一样,好奇怪。等理解了再更新。
3.参考资料
AI解答的内容。
以上就是本次笔记的记录,这个课还是没理解透,先做个记录,后面再更新。
