MIT-大整数相乘和大矩阵相乘
文章目录
- 大整数相乘(与多项式乘法类似)
- 问题描述
- 例子
- 算法实现
- 暴力算法
- 分治算法
- 大矩阵相乘
- 问题描述
- 例子
- 算法实现
- 暴力算法
- 分治算法
- Strassen算法(分治算法的优化)
大整数相乘(与多项式乘法类似)
问题描述
给定两个非负整数 AAA 和 BBB ,它们的位数可以非常大(可能有数千甚至数百万位)。要求计算它们的积:
C=A⋅BC = A\cdot BC=A⋅B
由于整数过大,无法直接使用内置整型存储,因此我们通常将每个大整数表示为:
A=(an−1an−2…a1a0),B=(bm−1bm−2…b1b0)A=(a_{n-1}a_{n-2}\ldots a_1a_0),\quad B=(b_{m-1}b_{m-2}\ldots b_1b_0)A=(an−1an−2…a1a0),B=(bm−1bm−2…b1b0)
例子
1 2 3 4× 5 6 7 8
---------------------------------------------9 8 7 2 (1234 × 8)8 6 3 8 (1234 × 7, 左移一位)7 4 0 4 (1234 × 6, 左移两位)+ 6 1 7 0 (1234 × 5, 左移三位)
---------------------------------------------7 0 0 6 6 5 2
算法实现
暴力算法
首先想到的就是小学学过的竖式计算法则,模拟我们手工笔算乘法的过程。即按每一位与另一数的每一位相乘,再把结果按位数对齐相加(考虑进位)。
vector<int> brute_Multiply(vector<int>& A, vector<int>& B)
{int n = A.size();int m = B.size();vector<int> res(n + m, 0);// 按位乘for (int i = 0; i < n; i ++ )for (int j = 0; j < m; j ++ )res[i + j] += A[i] * B[j];// 处理进位for (int i = 0; i < n + m; i ++ )if (res[i] > 9)res[i + 1] += res[i] / 10, res[i] = res[i] % 10;// 去除前导 0while (res.size() > 1 && res.back() == 0) res.pop_back();return res;
}
时间复杂度:O(nm)O(nm)O(nm)
分治算法
在大整数乘法中,我们可以把两个 nnn 位的数分为前半部分和后半部分,然后用子问题的结果拼接出整体乘积。这种思想实际上是对“竖式法”的系统化抽象:我们把数字分块计算,再根据块的位置(权值)把结果加回来。
我们假设 nnn 是 2 的幂,则有:
u=w2n/2+xv=y2n/2+z\begin{gathered}u = w 2^{n / 2} + x\\v = y 2^{n / 2} + z\end{gathered}u=w2n/2+xv=y2n/2+z
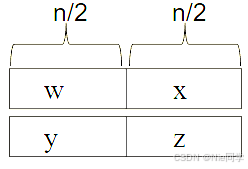
则 uvuvuv 的乘积为:
uv=(w2n/2+x)(y2n/2+z)=wy2n+(xy+wz)2n/2+xzuv=(w2^{n/2}+x)(y2^{n/2}+z)=wy2^n+(xy+wz)2^{n/2}+xzuv=(w2n/2+x)(y2n/2+z)=wy2n+(xy+wz)2n/2+xz
进一步 xy+wz=(w+x)(y+z)−wy−xzxy + wz = (w + x)(y + z) - wy - xzxy+wz=(w+x)(y+z)−wy−xz
故可以写成:
uv=wy2n+((w+x)(y+z)−wy−xz)2n/2+xzuv=wy2^{n}+((w+x)(y+z)-wy-xz)2^{n/2}+xzuv=wy2n+((w+x)(y+z)−wy−xz)2n/2+xz
MIT-两个多项式相乘:其实都是一类的问题,大整数相乘不就是多项式乘法代入具体数值吗?代码和时间复杂度分析直接参考这篇文章。
时间复杂度:O(nlog23)O(n^{\log_23})O(nlog23)
大矩阵相乘
问题描述
设矩阵 AAA 的大小为 m×nm \times nm×n,矩阵 BBB 的大小为 n×pn \times pn×p。则它们的乘积矩阵 CCC 的大小为 m×pm \times pm×p,定义为:
C=A×BC = A \times BC=A×B
其中
Cij=∑k=1mAik×Bkj(1≤i≤n,1≤j≤p)C_{ij}=\sum_{k=1}^mA_{ik}\times B_{kj}\quad(1\leq i\leq n,1\leq j\leq p)Cij=k=1∑mAik×Bkj(1≤i≤n,1≤j≤p)
例子
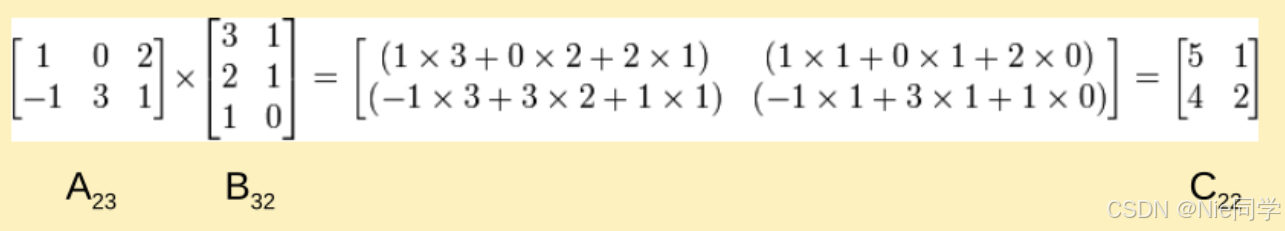
算法实现
暴力算法
首先想到的是直接按照矩阵乘法的运算规则,进行按位相乘再相加,即:
Cij=∑k=1mAik×Bkj(1≤i≤n,1≤j≤p)C_{ij}=\sum_{k=1}^mA_{ik}\times B_{kj}\quad(1\leq i\leq n,1\leq j\leq p)Cij=k=1∑mAik×Bkj(1≤i≤n,1≤j≤p)
for (int k = 1; k <= m; k ++ )for (int i = 1; i <= n; i ++ )for (int j = 1; j <= p; j ++ )C[i][j] = A[i][k] * B[k][j];
时间复杂度:O(nmp)O(nmp)O(nmp),若n=m=pn=m=pn=m=p ,则时间复杂度为 O(n3)O(n^3)O(n3)。
分治算法
将大矩阵划分成若干个小矩阵块,将矩阵乘法问题分解为几个小规模的矩阵乘法,再递归地求解并合并结果。
假设有两个 n×nn\times nn×n 的矩阵 AAA 和 BBB,把它们分别划分为 4 个 n2×n2\frac{n}{2} \times \frac{n}{2}2n×2n 的子矩阵:
A=[A11A12A21A22],B=[B11B12B21B22]A=\begin{bmatrix}A_{11}&A_{12}\\A_{21}&A_{22}\end{bmatrix},\quad B=\begin{bmatrix}B_{11}&B_{12}\\B_{21}&B_{22}\end{bmatrix}A=[A11A21A12A22],B=[B11B21B12B22]
则它们的乘积 C=A×BC=A\times BC=A×B 为:
C=[C11C12C21C22]C=\begin{bmatrix}C_{11}&C_{12}\\C_{21}&C_{22}\end{bmatrix}C=[C11C21C12C22]
其中每个子块的计算方式为:
C11=A11B11+A12B21C12=A11B12+A12B22C21=A21B11+A22B21C22=A21B12+A22B22\begin{aligned} C_{11} &= A_{11}B_{11} + A_{12}B_{21} \\ C_{12} &= A_{11}B_{12} + A_{12}B_{22} \\ C_{21} &= A_{21}B_{11} + A_{22}B_{21} \\ C_{22} &= A_{21}B_{12} + A_{22}B_{22} \end{aligned}C11C12C21C22=A11B11+A12B21=A11B12+A12B22=A21B11+A22B21=A21B12+A22B22
定义:typedef vector<vector<int>> Matrix
矩阵加法
Matrix addMatrix(Matrix& A, Matrix& B) {int n = A.size();int m = A[0].size();Matrix C(n, vector<int>(m, 0));for (int i = 0; i < n; i ++ )for (int j = 0; j < m; j ++ )C[i][j] = A[i][j] + B[i][j];return C;
}
矩阵减法
Matrix subMatrix(Matrix& A, Matrix& B) {int n = A.size();int m = A[0].size();Matrix C(n, vector<int>(m, 0));for (int i = 0; i < n; i ++ )for (int j = 0; j < m; j ++ )C[i][j] = A[i][j] - B[i][j];return C;
}
分治矩阵
Matrix DC_divideConquerMultiply(Matrix& A, Matrix& B) {int n = A.size();// 基本情况:1x1矩阵if (n == 1) {return {{A[0][0] * B[0][0]}};}int mid = n / 2;// 划分子矩阵Matrix A11(mid, vector<int>(mid)), A12(mid, vector<int>(mid));Matrix A21(mid, vector<int>(mid)), A22(mid, vector<int>(mid));Matrix B11(mid, vector<int>(mid)), B12(mid, vector<int>(mid));Matrix B21(mid, vector<int>(mid)), B22(mid, vector<int>(mid));for (int i = 0; i < mid; i++) {for (int j = 0; j < mid; j++) {A11[i][j] = A[i][j];A12[i][j] = A[i][j + mid];A21[i][j] = A[i + mid][j];A22[i][j] = A[i + mid][j + mid];B11[i][j] = B[i][j];B12[i][j] = B[i][j + mid];B21[i][j] = B[i + mid][j];B22[i][j] = B[i + mid][j + mid];}}// 递归计算子矩阵Matrix C11 = addMatrix(DC_divideConquerMultiply(A11, B11),DC_divideConquerMultiply(A12, B21));Matrix C12 = addMatrix(DC_divideConquerMultiply(A11, B12),DC_divideConquerMultiply(A12, B22));Matrix C21 = addMatrix(DC_divideConquerMultiply(A21, B11),DC_divideConquerMultiply(A22, B21));Matrix C22 = addMatrix(DC_divideConquerMultiply(A21, B12),DC_divideConquerMultiply(A22, B22));// 合并四个子矩阵Matrix C(n, vector<int>(n, 0));for (int i = 0; i < mid; i++) {for (int j = 0; j < mid; j++) {C[i][j] = C11[i][j];C[i][j + mid] = C12[i][j];C[i + mid][j] = C21[i][j];C[i + mid][j + mid] = C22[i][j];}}return C;
}
假设 n=2hn=2^hn=2h 且 T(1)=O(1)T(1)=O(1)T(1)=O(1),T(n)T(n)T(n) 是执行两个 n×nn \times nn×n 矩阵乘法所需的时间。
- A11B11A_{11}B_{11}A11B11:T(n2)T(\frac{n}{2})T(2n)
- …
- A22B22A_{22}B_{22}A22B22:T(n2)T(\frac{n}{2})T(2n)
- A11B11+A12B21A_{11}B_{11} + A_{12}B_{21}A11B11+A12B21:O((n2)2)O((\frac{n}{2})^2)O((2n)2)
- …
- A21B12+A22B22A_{21}B_{12} + A_{22}B_{22}A21B12+A22B22:O((n2)2)O((\frac{n}{2})^2)O((2n)2)
可知矩阵乘法有 8 次,而矩阵加法有 4 次。
T(n)=8T(n2)+O(n2)=8[8T(n22)]+O(n2)=82T(n22)+O(n2)=...=8hT(n2h)+O(n2)=(2h)3T(n2h)+O(n2)=n3T(1)+O(n2)=O(n3)\begin{aligned} T(n)&=8T({\frac{n}{2}})+O(n^2) \\&=8\left[8T(\frac{n}{2^2})\right]+O(n^2) \\&=8^2T(\frac{n}{2^2})+O(n^2) \\&=... \\&=8^hT(\frac{n}{2^h})+O(n^2) \\&=(2^h)^3T(\frac{n}{2^h})+O(n^2) \\&=n^3T(1)+O(n^2) \\&=O(n^3) \end{aligned}T(n)=8T(2n)+O(n2)=8[8T(22n)]+O(n2)=82T(22n)+O(n2)=...=8hT(2hn)+O(n2)=(2h)3T(2hn)+O(n2)=n3T(1)+O(n2)=O(n3)
Strassen算法(分治算法的优化)
依旧采用 MIT-两个多项式相乘 的优化分治算法的思想,通过数学的等式变换,从而通过增加加减法的次数而减少算法中乘法的计算次数。
与分治算法定义的一样,先将矩阵 AAA 和 BBB 分成 4 个子块:
A=[A11A12A21A22],B=[B11B12B21B22]A=\begin{bmatrix}A_{11}&A_{12}\\A_{21}&A_{22}\end{bmatrix},\quad B=\begin{bmatrix}B_{11}&B_{12}\\B_{21}&B_{22}\end{bmatrix}A=[A11A21A12A22],B=[B11B21B12B22]
Strassen 定义 7 个中间矩阵:
M1=(A11+A22)(B11+B22)M2=(A21+A22)B11M3=A11(B12−B22)M4=A22(B21−B11)M5=(A11+A12)B22M6=(A21−A11)(B11+B12)M7=(A12−A22)(B21+B22)\begin{aligned}&M_{1}=(A_{11}+A_{22})(B_{11}+B_{22})\\&M_2=(A_{21}+A_{22})B_{11}\\&M_3=A_{11}(B_{12}-B_{22})\\&M_{4}=A_{22}(B_{21}-B_{11})\\&M_{5}=(A_{11}+A_{12})B_{22}\\&M_{6}=(A_{21}-A_{11})(B_{11}+B_{12})\\&M_{7}=(A_{12}-A_{22})(B_{21}+B_{22})\end{aligned}M1=(A11+A22)(B11+B22)M2=(A21+A22)B11M3=A11(B12−B22)M4=A22(B21−B11)M5=(A11+A12)B22M6=(A21−A11)(B11+B12)M7=(A12−A22)(B21+B22)
再通过加减组合出最终结果:
C11=M1+M4−M5+M7C12=M3+M5C21=M2+M4C22=M1−M2+M3+M6\begin{aligned}&C_{11}=M_1+M_4-M_5+M_7\\&C_{12}=M_3+M_5\\&C_{21}=M_2+M_4\\&\mathrm{C_{22}}=M_1-M_2+M_3+M_6\end{aligned}C11=M1+M4−M5+M7C12=M3+M5C21=M2+M4C22=M1−M2+M3+M6
Matrix StrassenMultiply(Matrix& A, Matrix& B) {int n = A.size();if (n == 1) return {{A[0][0] * B[0][0]}};int mid = n / 2;// 划分子矩阵Matrix A11(mid, vector<int>(mid)), A12(mid, vector<int>(mid));Matrix A21(mid, vector<int>(mid)), A22(mid, vector<int>(mid));Matrix B11(mid, vector<int>(mid)), B12(mid, vector<int>(mid));Matrix B21(mid, vector<int>(mid)), B22(mid, vector<int>(mid));for (int i = 0; i < mid; i++)for (int j = 0; j < mid; j++) {A11[i][j] = A[i][j];A12[i][j] = A[i][j + mid];A21[i][j] = A[i + mid][j];A22[i][j] = A[i + mid][j + mid];B11[i][j] = B[i][j];B12[i][j] = B[i][j + mid];B21[i][j] = B[i + mid][j];B22[i][j] = B[i + mid][j + mid];}// Strassen 7 个中间矩阵Matrix M1 = StrassenMultiply(addMatrix(A11, A22), addMatrix(B11, B22));Matrix M2 = StrassenMultiply(addMatrix(A21, A22), B11);Matrix M3 = StrassenMultiply(A11, subMatrix(B12, B22));Matrix M4 = StrassenMultiply(A22, subMatrix(B21, B11));Matrix M5 = StrassenMultiply(addMatrix(A11, A12), B22);Matrix M6 = StrassenMultiply(subMatrix(A21, A11), addMatrix(B11, B12));Matrix M7 = StrassenMultiply(subMatrix(A12, A22), addMatrix(B21, B22));// 组合出结果矩阵Matrix C11 = addMatrix(subMatrix(addMatrix(M1, M4), M5), M7);Matrix C12 = addMatrix(M3, M5);Matrix C21 = addMatrix(M2, M4);Matrix C22 = addMatrix(subMatrix(addMatrix(M1, M3), M2), M6);// 合并四个子矩阵Matrix C(n, vector<int>(n, 0));for (int i = 0; i < mid; i++)for (int j = 0; j < mid; j++) {C[i][j] = C11[i][j];C[i][j + mid] = C12[i][j];C[i + mid][j] = C21[i][j];C[i + mid][j + mid] = C22[i][j];}return C;
}
时间复杂度:O(nlog27)≈O(n2.81)O(n^{\log_27})\approx O(n^{2.81})O(nlog27)≈O(n2.81)
假设 n=2hn=2^hn=2h 且 T(1)=O(1)T(1)=O(1)T(1)=O(1),T(n)T(n)T(n) 是执行两个 n×nn \times nn×n 矩阵乘法所需的时间。
可知矩阵乘法有 7 次,而矩阵加法有 18 次。
T(n)=7T(n2)+O(n2)=7[7T(n22)]+O(n2)=72T(n22)+O(n2)=...=7hT(n2h)+O(n2)=(2log27)hT(n2h)+O(n2)=(2h)log27T(n2h)+O(n2)=nlog27T(1)+o(n2)=O(nlog27)\begin{aligned} T(n)&=7T({\frac{n}{2}})+O(n^2) \\&=7\left[7T(\frac{n}{2^2})\right]+O(n^2) \\&=7^2T(\frac{n}{2^2})+O(n^2) \\&=... \\&=7^hT(\frac{n}{2^h})+O(n^2) \\&=(2^{\log_2 7})^hT(\frac{n}{2^h})+O(n^2) \\&=(2^h)^{\log_2 7}T(\frac{n}{2^h})+O(n^2) \\&=n^{\log_27}T(1)+o(n^2) \\&=O(n^{\log_27}) \end{aligned}T(n)=7T(2n)+O(n2)=7[7T(22n)]+O(n2)=72T(22n)+O(n2)=...=7hT(2hn)+O(n2)=(2log27)hT(2hn)+O(n2)=(2h)log27T(2hn)+O(n2)=nlog27T(1)+o(n2)=O(nlog27)
