【AI?】
25082508 2508
从函数到神经网络
- 符号主义
符号主义
函数可以表示一切
func describe the world


问题来了,找不到足够丝滑的函数「难以找到」
- 联结主义
联结主义
猜&简化
先猜一个函数f(x)=wx+bf(x)=wx+bf(x)=wx+b,然后不断调整w和b,逐渐逼近真实答案「一个足够接近真实答案的近似解」
f(x)=wx+bf(x)=wx+b f(x)=wx+b
找不到完全吻合的函数,差不多就行了「简化问题」
效果出乎意料的好,很少的参数即可实现任务。
问题:f(x)=wx+bf(x)=wx+bf(x)=wx+b线性函数太简单,不足以描述更复杂的关系
- 激活函数
激活函数
把原本死气沉沉的线性关系,盘活了。「比如平方,将直线变为抛物线」
注意:每个输入xix_ixi都要对应一个wiw_iwi。
f(x)=g(wx+b)f(x)=\textcolor {red}{g(}wx+b\textcolor {red}{)} f(x)=g(wx+b)


通过线性变换和非线性激活函数的不断组合和套娃,可以表达很复杂的关系
f(x1,x2)=g(w3g(w1x1+w2x2+b)+b2)f(x_1,x_2)=g(w_3{\color{gray}g(w_1x_1+w_2x_2+b)}+b_2) f(x1,x2)=g(w3g(w1x1+w2x2+b)+b2)
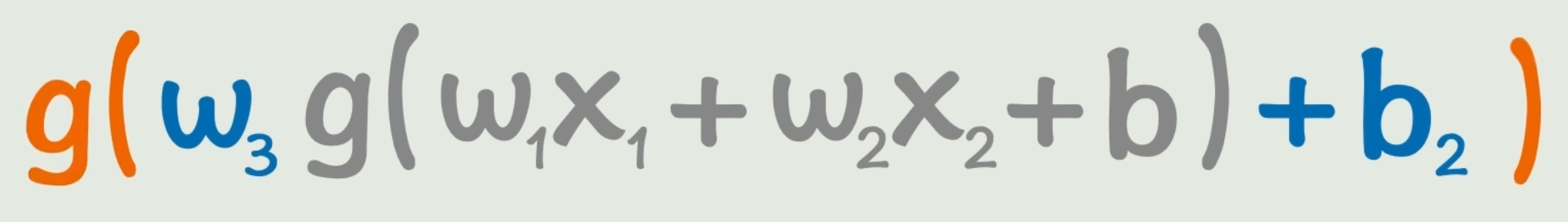
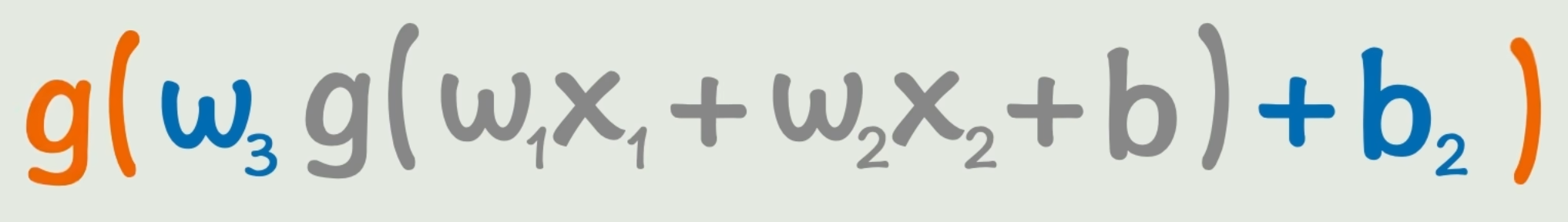
但是写成函数看太恶心了,所以画成了「神经网络」
- 神经网络
神经网络
每个小圈称为「神经元」。
中间结果「或者说前半部分计算结果」称为「隐藏层」。
从左到右一点点把函数计算出来,称为「前向传播」。
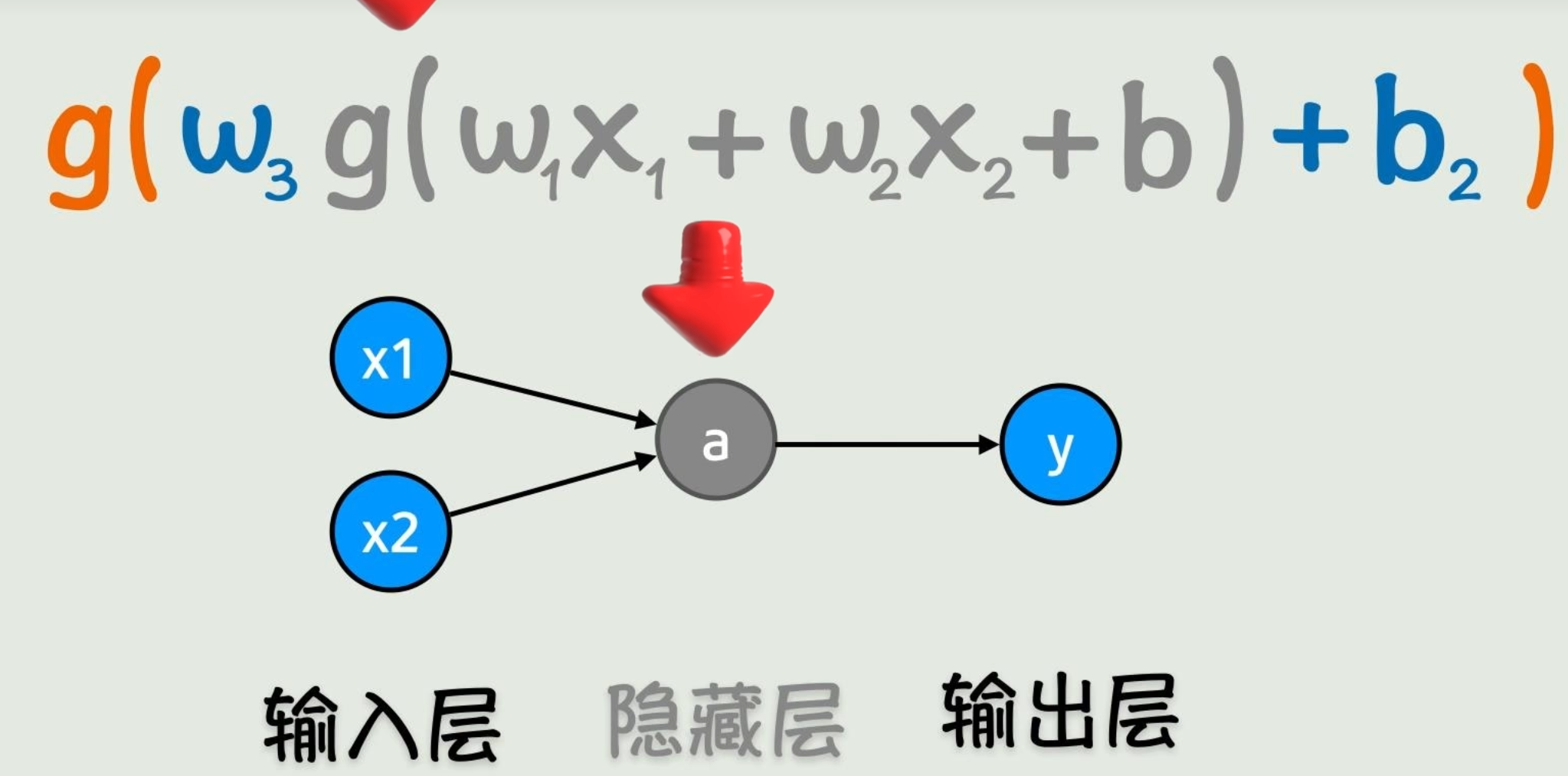
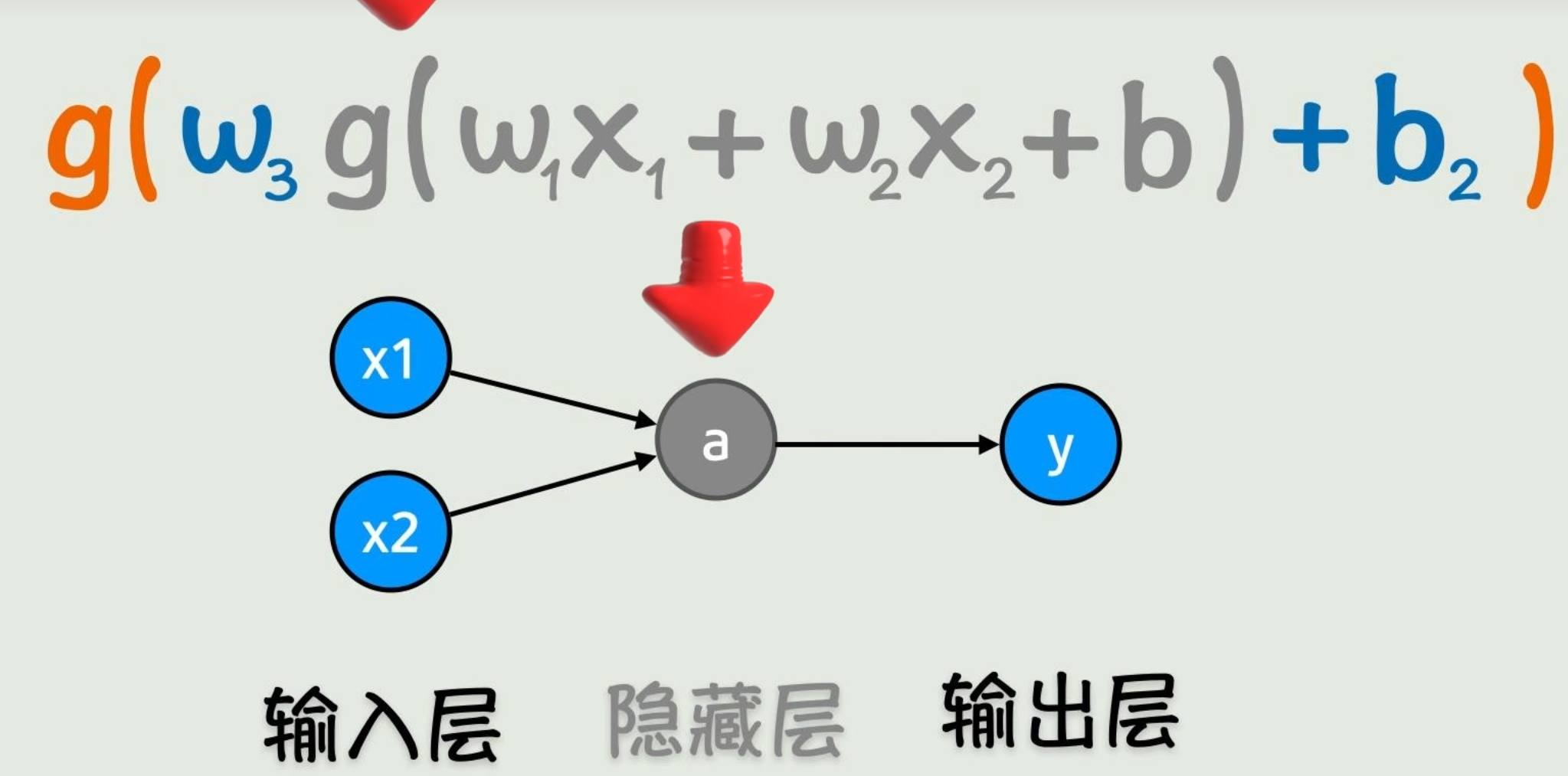
我们的目的:求出w、b,使这个函数可以很好的拟合真实数据「已知的输入x」
总结
从符号主义试图用完美函数描述世界却因规律难寻遇阻,到联结主义退而求其次用简单线性函数f(x)=wx+b“连蒙带猜”近似规律,虽凭少量参数简化问题但受限于线性表达能力;随后激活函数通过非线性变换“盘活”线性关系,让每个输入x对应独立权重w,再经“线性变换+非线性激活”的多层套娃实现复杂关系建模;而神经网络正是这种嵌套结构的可视化呈现,其核心目标始终是求解最优权重w和偏置b,以精准拟合真实数据。
计算神经网络的参数
本节目的:
1. 如何量化「拟合程度」?
2. 找一个线性函数f(x),称「线性回归」。
3.
问题:什么样的w、b才是好的呢?
拟合的好,才是真的好。
问题:什么叫「拟合的好」?如何表达?
- 损失函数
损失函数&均方误差&线性回归
预测数据与真实数据之间差距的总和。可以反映当前这个线性函数跟与真实数据的拟合度。
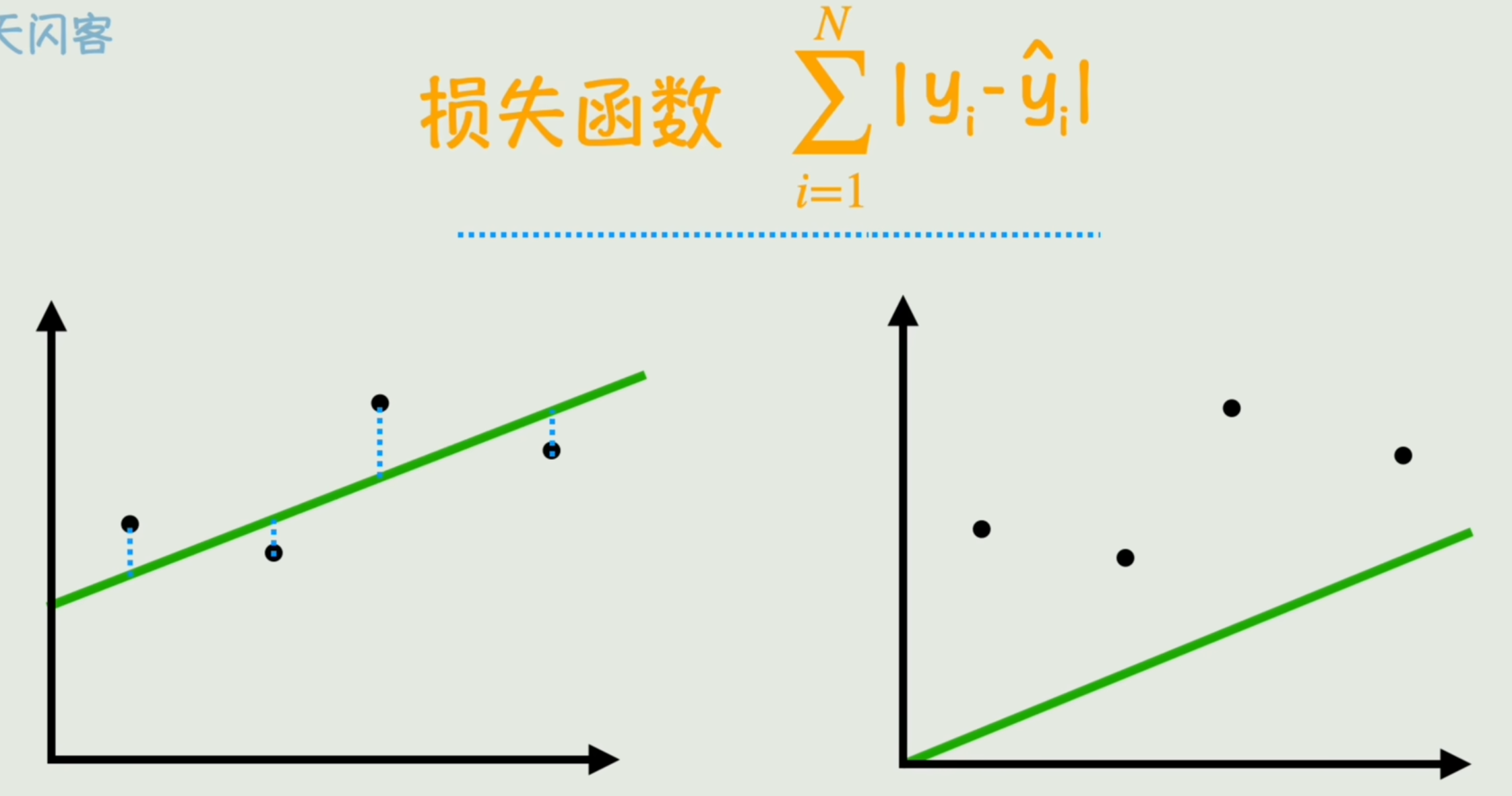
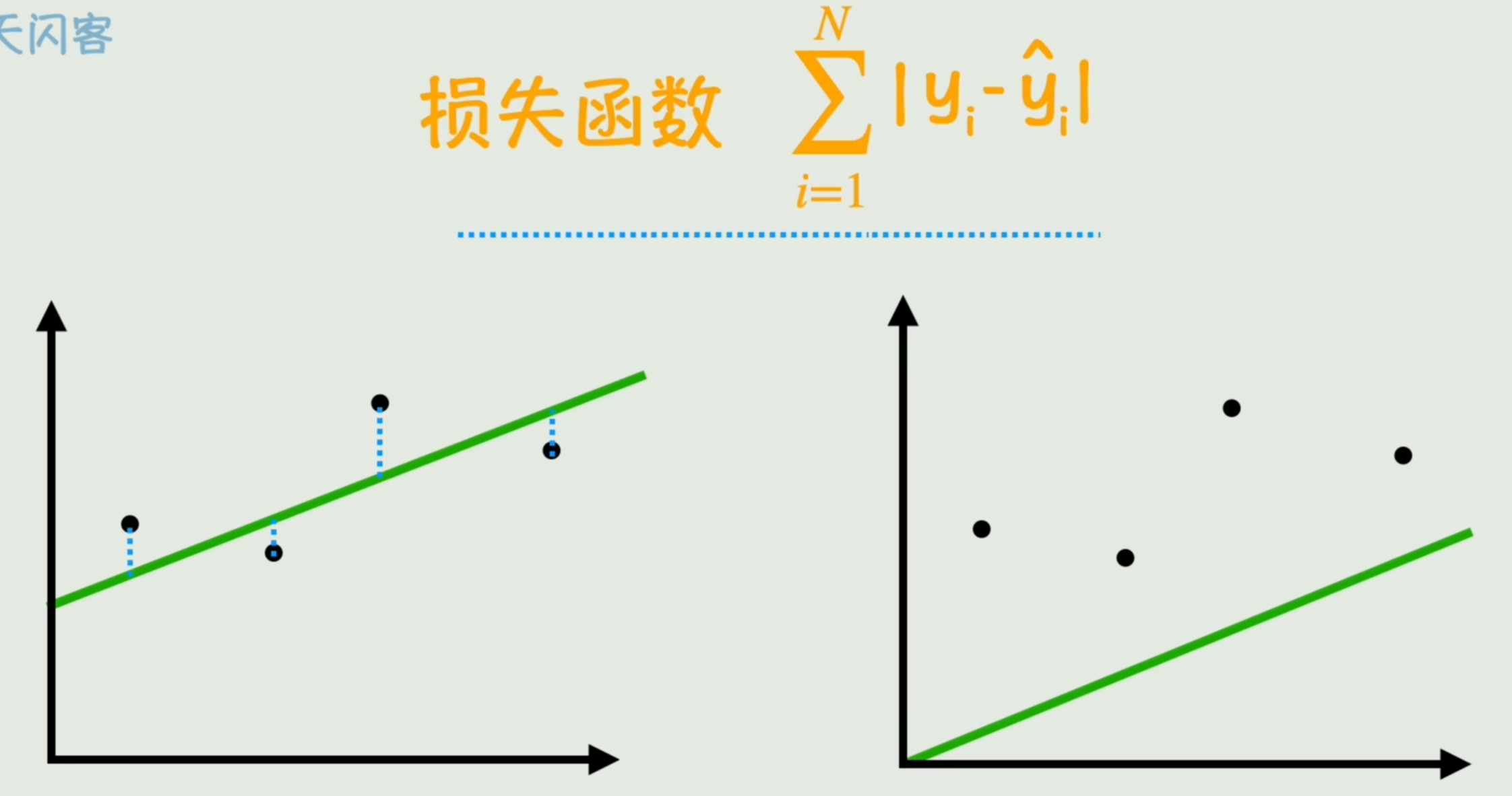
- 最小二乘法
带绝对值不够平滑,求平方。这种优化方法称为「最小二乘法」。
再根据验本数量平均一下,消除样本数量大小的影响,就得到了一种计算损失的函数:
- 均方误差(Mean-Square Error, MSE)
Loss(w,b)=1N∑i=1N(yi−yi^)2Loss(w,b)=\frac1{N}\sum_{i=1}^{N}(y_i-\hat{y_i})^2 Loss(w,b)=N1i=1∑N(yi−yi^)2
目标:求让Loss函数最小的那个点,对应的w和b。
方法:让该损失函数的导数=0,求极值点。
因为是关于w和b的二元函数,因此要求出「偏导」(固定一方为常数)。
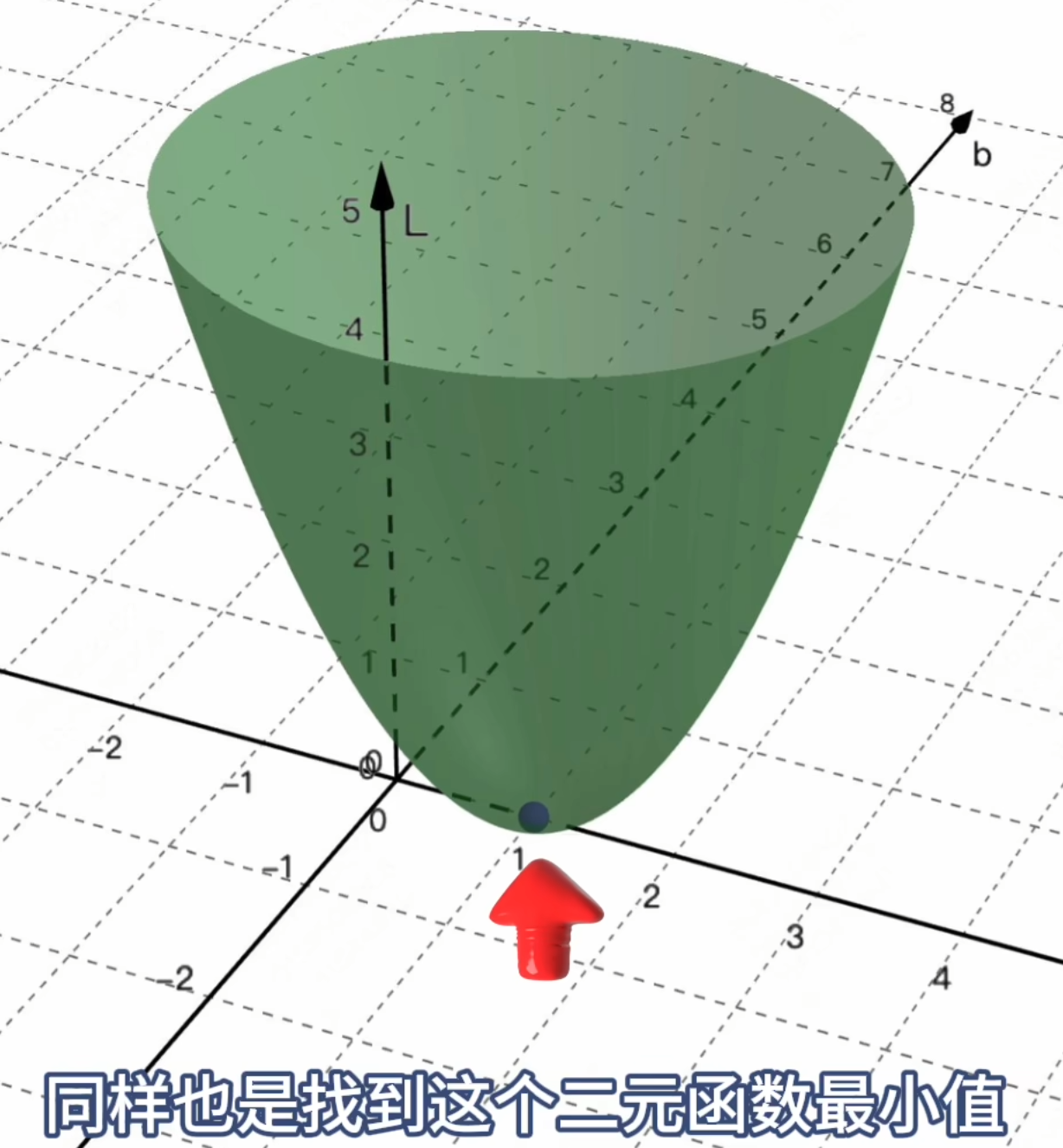
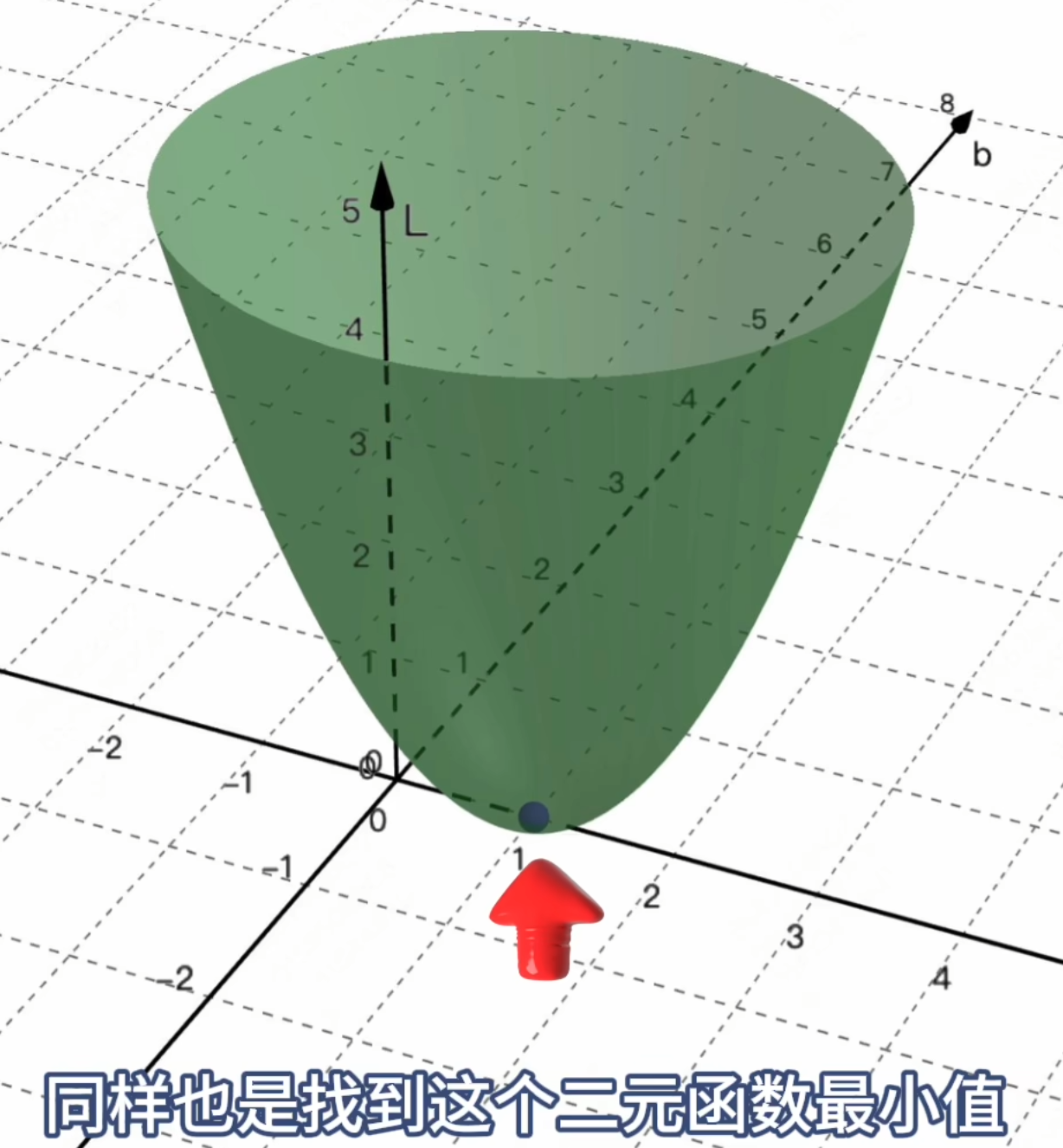
上面这个「通过寻找==一个线性函数==,来拟合x和y的关系」,就是机器学习中最基本的一种分析方法:「线性回归」
- 线性回归
神经网络是通过线性函数与非线性激活函数的不断组合和套娃,形成的一种极为复杂的非线性函数模型。
其损失函数是远比一个线性函数要复杂的非线性函数,往往不能导数=0直接求出最小值,那该怎么办呢?
- 梯度下降
梯度下降
简单粗暴:一点点试。
增大w,若Loss减小,则继续增大w。b同理。「直到让Loss足够小」
w变化一点使得Loss会变化多少,其实就是损失函数对w的偏导数 ∂L(w,b)∂w\frac{\partial L(w, b)}{\partial w}∂w∂L(w,b) 。b同理。
我们要做的就是让w和b向偏导数「梯度」的反方向变化,变化的快慢(变化幅度)再加一个系数η\etaη「学习率」来控制:
wnew=w−η∂L(w,b)∂ww_{new} = w-\eta\frac{\partial L(w, b)}{\partial w} wnew=w−η∂w∂L(w,b)
解释:为何朝着偏导数「梯度」的反方向变化?
调整方向:反着偏导数来
- 如果 (∂L(w,b)∂w\frac{\partial L(w, b)}{\partial w}∂w∂L(w,b)) 是 正的「正相关」:说明 w 越大 Loss 越大(或减小 w 会让 Loss 减小 )→ 为了让 Loss 变小,w 要减去梯度。
- 负相关同理,w越大Loss越小,w要加上梯度。
不管正负,让 w 向 “偏导数的反方向” 变化,就能一步步让 Loss 减小。
学习率 (η=0.01\eta=0.01η=0.01),就表示每次只按照 “偏导数的 1%” 来调整 w,慢慢逼近最优值。
不断变化w和b,让Loss逐渐减小,进而求出最终的w和b的过程,就叫「梯度下降」。
其中,「梯度」指的是所有参数偏导数的向量集合。对于含 w 和 b 两个参数的函数,梯度为 (∇L(w,b)=(∂L(w,b)∂w,∂L(w,b)∂b)\nabla L(w, b) = \left( \frac{\partial L(w, b)}{\partial w}, \frac{\partial L(w, b)}{\partial b} \right)∇L(w,b)=(∂w∂L(w,b),∂b∂L(w,b)))。它不仅包含每个参数的偏导数大小,还整体表示 Loss 函数在当前参数点上变化最快的方向和幅度.
问题又来了,有了求出最小值的公式「梯度下降」,但这个公式里的偏导数 ∂L(w,b)∂w\frac{\partial L(w, b)}{\partial w}∂w∂L(w,b) 怎么求呢?
- 链式法则
链式法则&反向传播&训练
神经网络整体虽然复杂,但层与层之间的关系却十分简单(一个非线性激活函数罢了)
以图中最难求的w1w_1w1为例「w2w_2w2、a同理,不过层数更少」,我们想知道w1w_1w1变化一个单位,损失函数Loss变化了多少。
先看w1w_1w1变化1单位,会使得a变化多少,再看a变化1单位,会使y^\hat yy^变化多少,再看y^\hat yy^变化1单位,会使Loss变化多少。将三者乘起来,就得到w1w_1w1变化1单位,损失函数Loss变化多少了。亦即我们想求的偏导数。
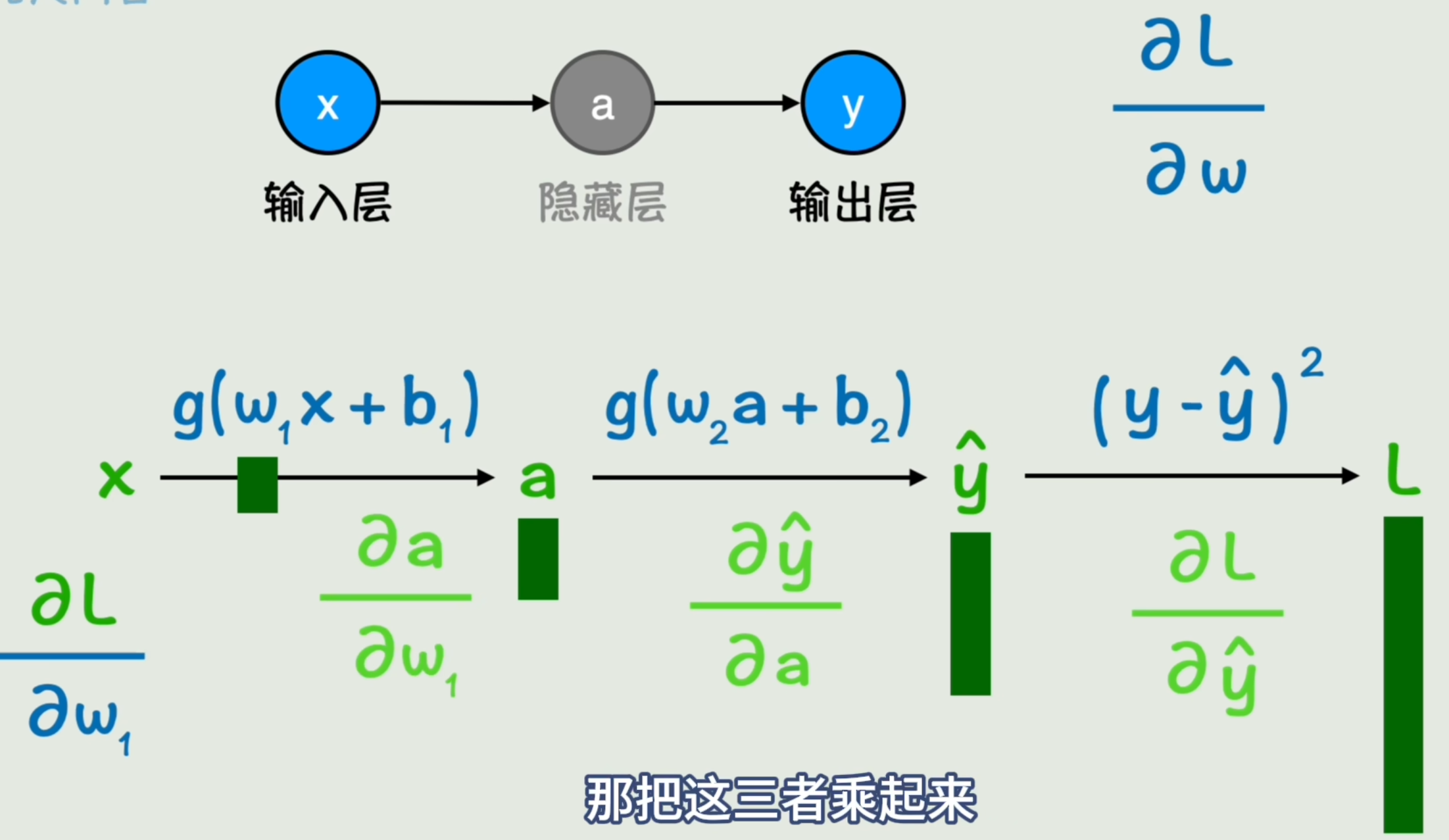
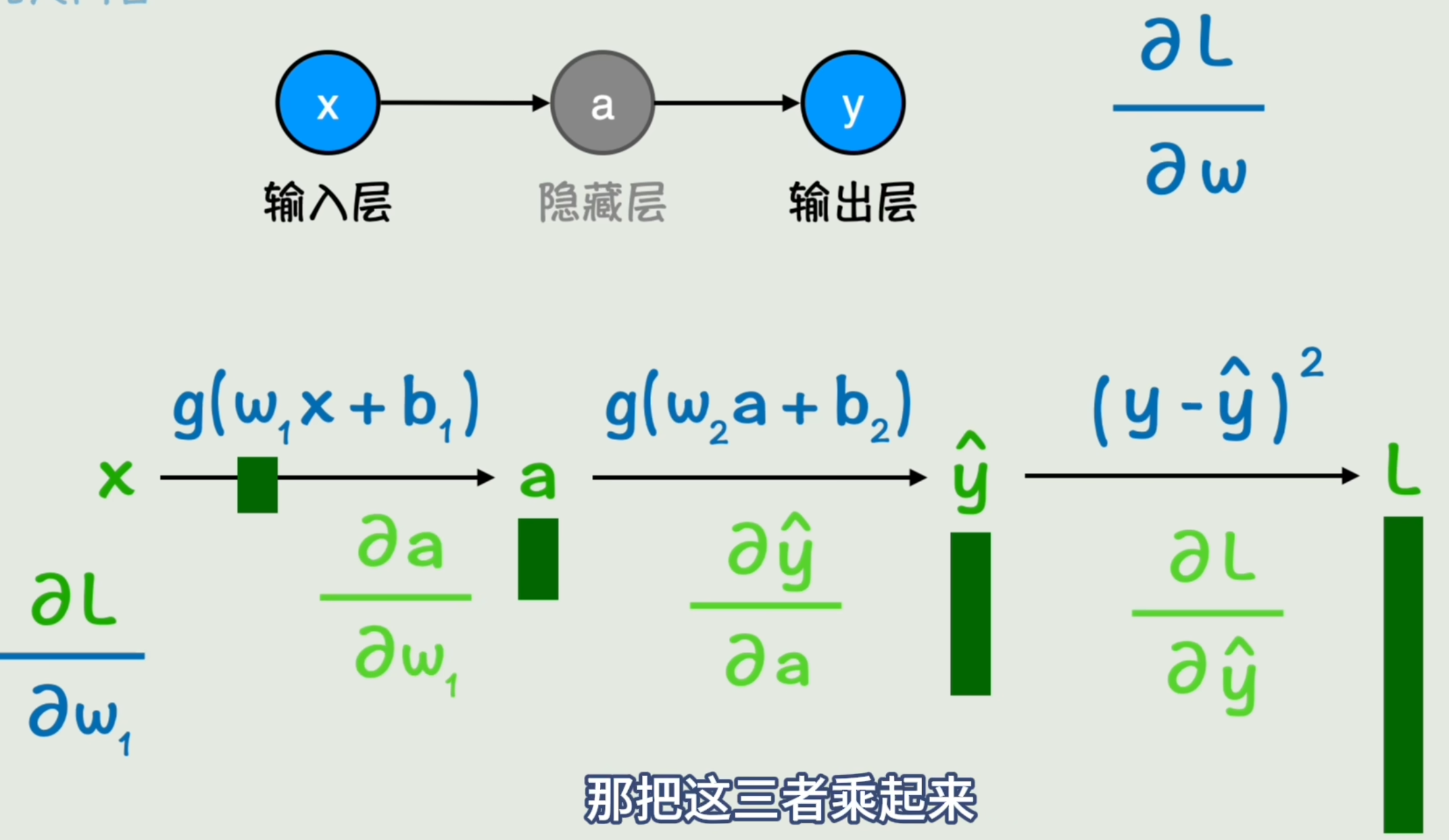
若想不通可以联想齿轮。计算第一个转一圈会使得最后一个转多少圈。
∂L∂w1=∂L∂y^∂y^∂a∂a∂w1\frac{\partial L}{\partial w_1}=\frac{\partial L}{\partial \hat y}\frac{\partial \hat y}{\partial a}\frac{\partial a}{\partial w_1} ∂w1∂L=∂y^∂L∂a∂y^∂w1∂a
这其实就是偏导数的链式求导,也称为「链式法则」。(微积分的复合函数求导)
由于我们可以从Loss开始自右向左依次求导,然后逐步更新每一层的参数w和b,而由于链式法则,前一层的偏导数的值后面也会用到,所以不用每次都重新计算,让这些值从右向左一点点传播过来即可。形象的称之为「反向传播」
- 反向传播
- 训练
根据之前的知识,我们通过输入x计算输出y,得到Loss后再通过反向传播计算损失函数关于每个参数的梯度,每个参数都向梯度的反方向变化一点点,这就完成了神经网络的一次训练。
通过一点点变化,直到损失函数足够小,就找到了我们想要的「符号」f(xn)f(x_n)f(xn)。
听起来简单,但真实问题往往存在各种难题。
总结
要判断w和b是否“好”,核心看模型对数据的「拟合程度」——而拟合好坏由损失函数量化:它计算预测值与真实值的差距总和,差距越小拟合越好。最常用的是均方误差(MSE),通过对误差平方后取平均(Loss(w,b)=1N∑i=1N(yi−yi^)2)(Loss(w,b)=\frac{1}{N}\sum_{i=1}^{N}(y_i-\hat{y_i})^2)(Loss(w,b)=N1∑i=1N(yi−yi^)2),既避免绝对值的不平滑,又消除样本数量影响。
目标是找到使Loss最小的w和b:
- 简单线性回归可直接求Loss函数导数为0的极值点(用偏导,因w、b是二元变量)。
- 但神经网络是复杂非线性模型,无法直接求解析解,需用梯度下降:通过“试错”调整w和b——每次沿Loss对w(或b)偏导数的反方向更新(因偏导正→增w会增Loss,需减w;偏导负则反之),更新幅度由学习率(η) 控制(w=w−η∂L∂w)(w = w-\eta\frac{\partial L}{\partial w})(w=w−η∂w∂L),逐步逼近Loss最小值。
梯度下降的关键是求偏导,神经网络多层结构需用链式法则:像齿轮传动,逐层计算参数变化对Loss的影响(如∂L∂w1=∂L∂y^⋅∂y^∂a⋅∂a∂w1)\frac{\partial L}{\partial w_1}=\frac{\partial L}{\partial \hat{y}}\cdot\frac{\partial \hat{y}}{\partial a}\cdot\frac{\partial a}{\partial w_1})∂w1∂L=∂y^∂L⋅∂a∂y^⋅∂w1∂a)。而从Loss出发自右向左逐层传递偏导值、更新参数的过程,就是反向传播。
最终,通过==“正向计算输出→算Loss→反向传播求梯度→梯度下降调参数”==的反复训练,直到Loss足够小,就得到了最优的w和b。
调教神经网络的方法
过拟合&泛化能力
只要构造一个足够复杂的函数「复杂神经网络」,那么不就可以表达世间万物了吗?
之前我们的目标是「拟合的好」,但过于复杂函数会出现一种在训练数据上表现完美「损失极小」,但在没见过数据上表现很糟糕的现象。
这种现象,我们称为「过拟合」。
在没见过数据上的表现,我们称为「泛化能力」
- 过拟合
- 泛化能力
如图所示的「复杂神经网络」的训练效果甚至不如一个线性模型。所以说模型并非越复杂越好(把噪声和随机波动也给学会了)。
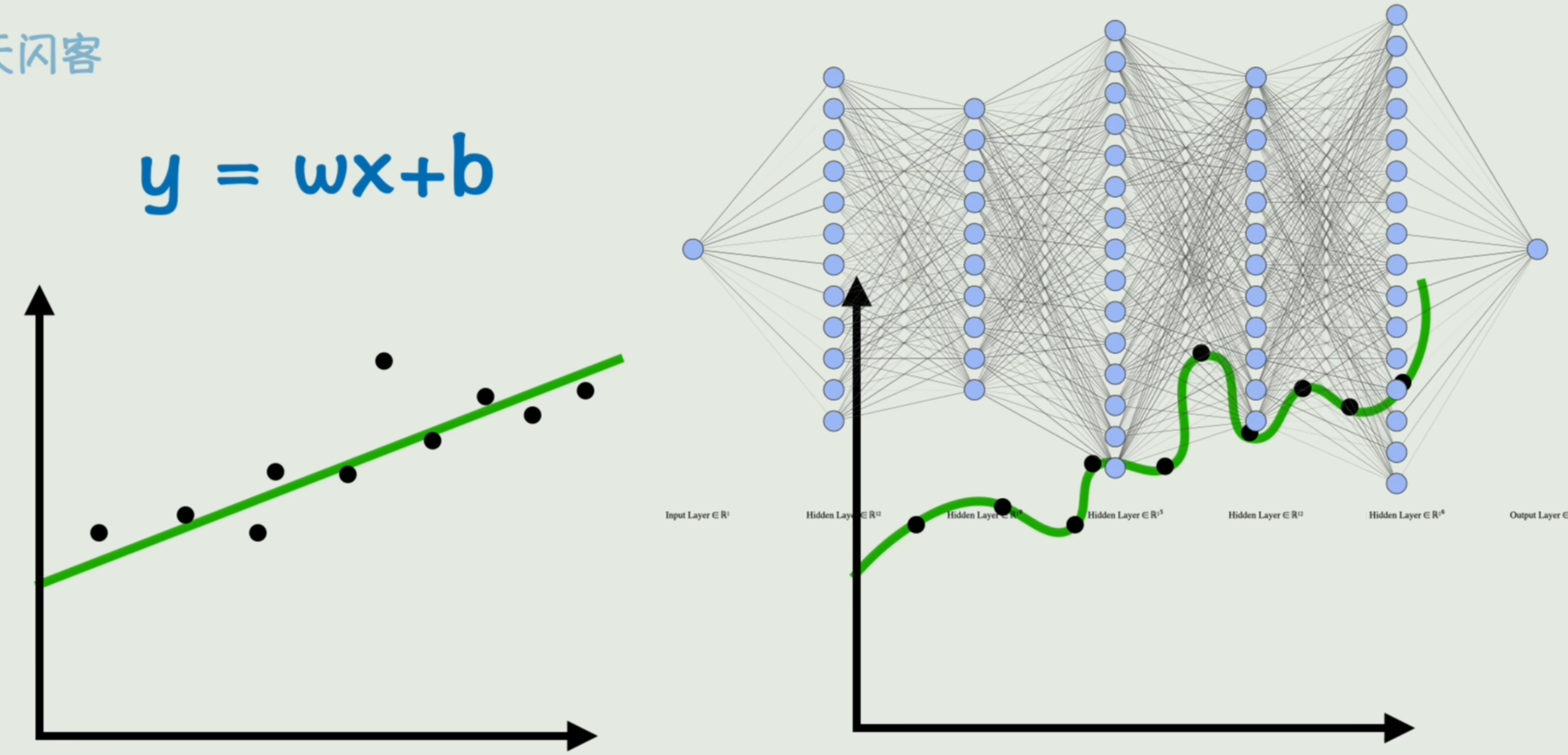
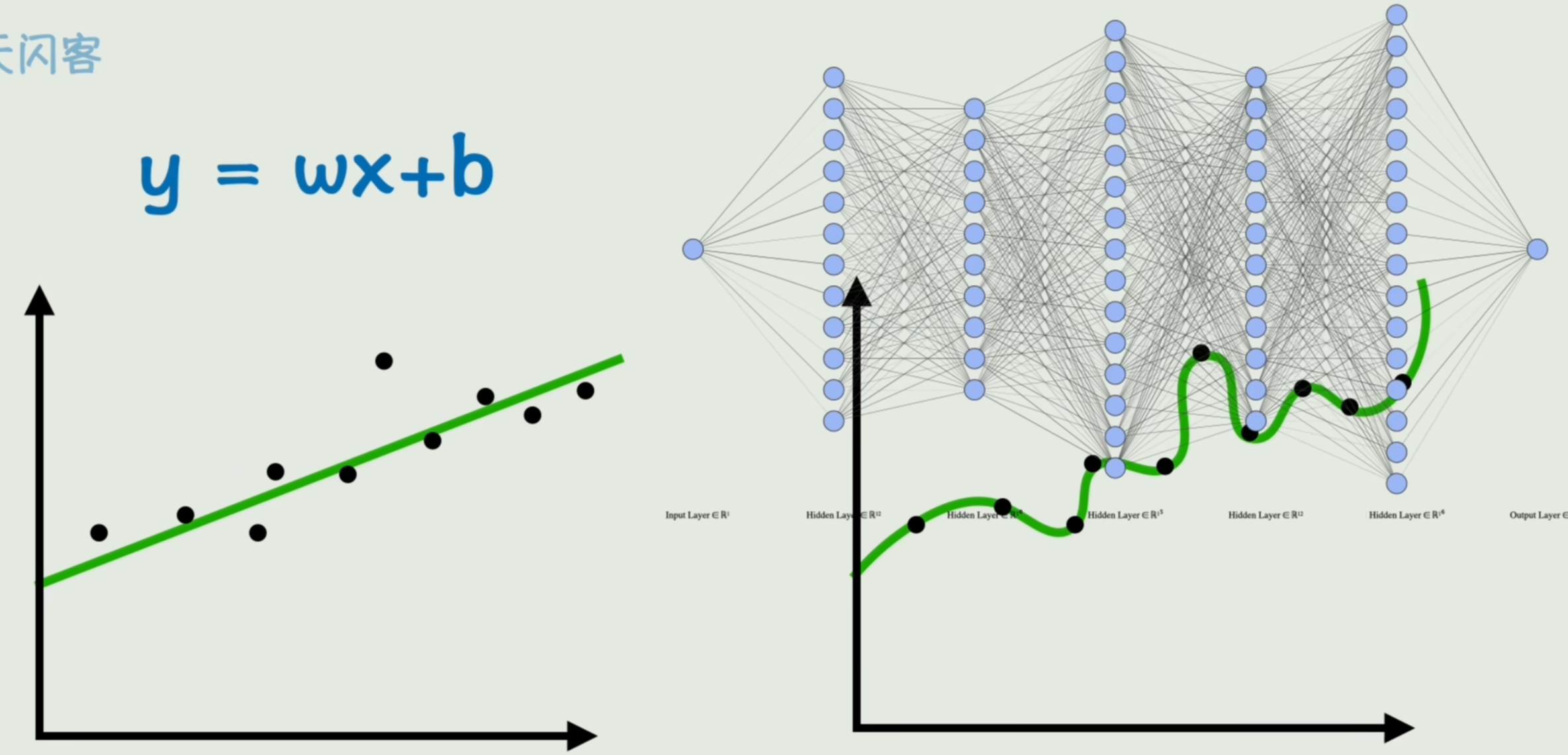
数据增强&正则化&Dropout
那么如何解决「过拟合」这个问题呢?
- 数据增强
第一种方法:从数据和模型本身入手,简化模型复杂度。
增加训练数据的量。相对的模型复杂度也会变简单「简单模型也能有效拟合」。「数据越多,模型受噪声影响越小(易区分规律与噪声)」
有时我们确实无法收集或懒得收集更多的数据,直接在原有数据基础上创造新的数据。比如在图像数据中,对图像进行旋转、翻转、裁剪、加噪声等操作,创建更多的训练样本。称为「数据增强」。刚好训练了一个不因输入一点小小变化,对结果产生很大波动的模型「鲁棒性」。
- 正则化
第二种方法:从训练过程入手,抑制参数野蛮生长。
训练本身就是不断调整参数的过程。有个简单到难以置信的方法:停止训练。
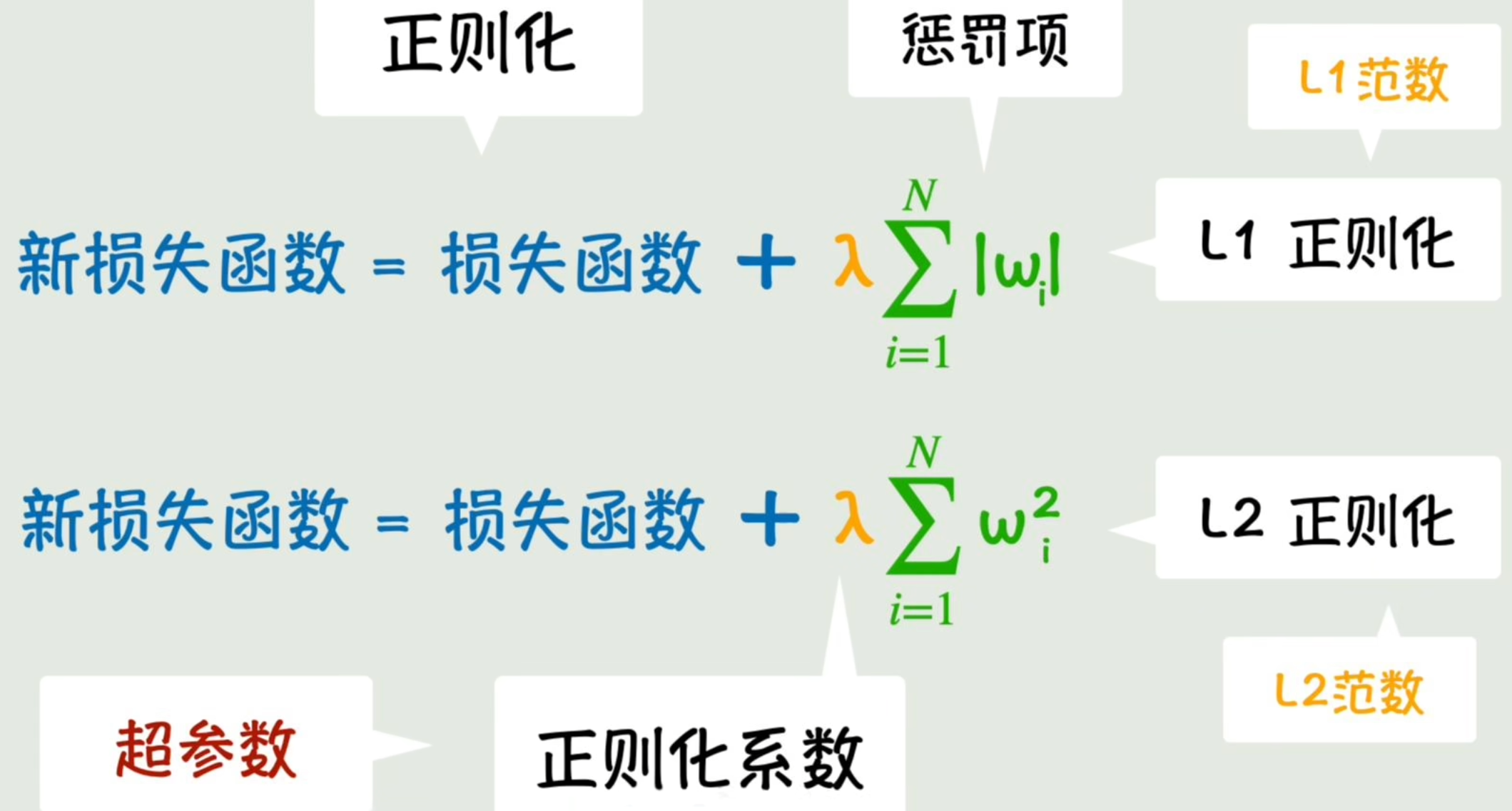
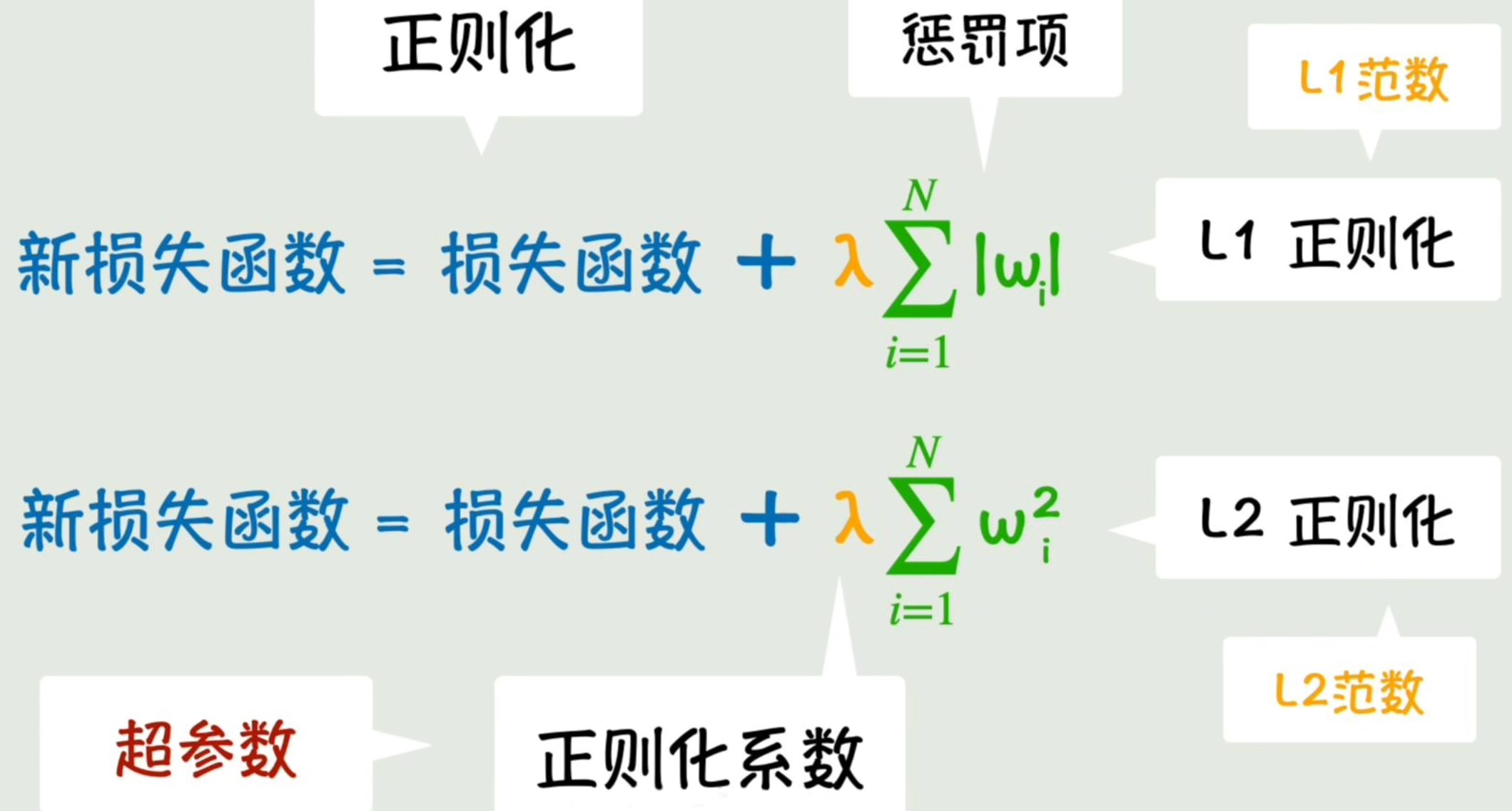
但模型会比较粗糙。更精细的抑制参数野蛮增长的方法:给损失函数**加上一项参数本身**的绝对值∣w∣|w|∣w∣「目标是让损失函数最小化,若参数增幅过大会让损失函数变大,达成抑制目的」,我们称该项为「惩罚项」。
同控制损失函数下降力度的「学习率」一样,给惩罚项增加一个控制惩罚力度的系数「正则化系数」。这种控制参数的参数,我们称之为「超参数」。
除此之外,还有一种简单到令人发指的方法。
- Dropout「暂时失效」
每次训练部分参数,临时简化模型结构,让整体参数都差不多。
为防止模型过度依赖少量参数,在训练过程中,每次随机丢弃部分参数,让模型不得不依赖更多的普通参数。结果表明,该方法抑制过拟合很有效。由深度学习之父 Hinton 提出。
其他
从矩阵到CNN
矩阵运算
- 矩阵运算
我们将神经网络的一层中麻烦的“加减乘除”写法替换为“矩阵运算”,如图所示:
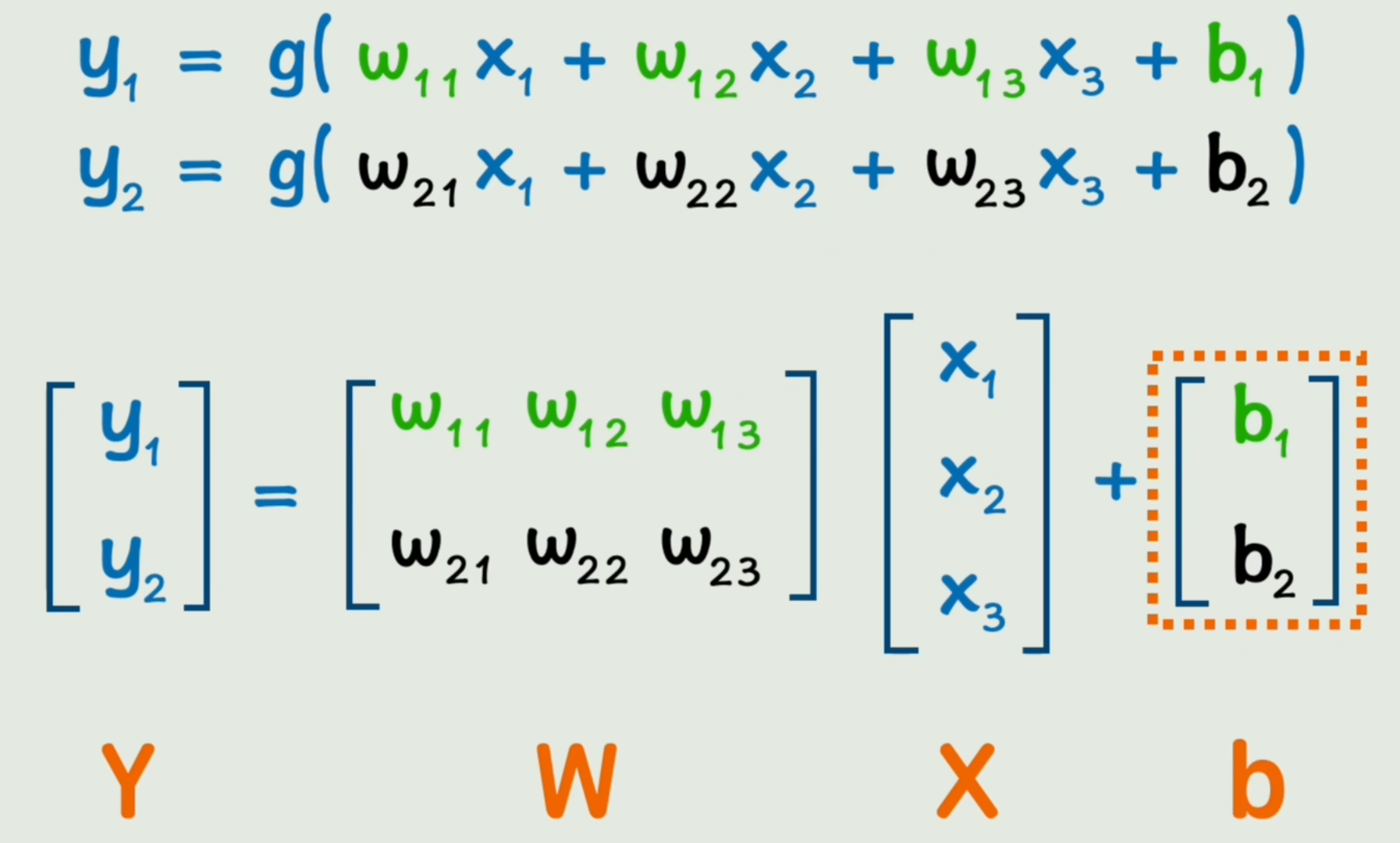
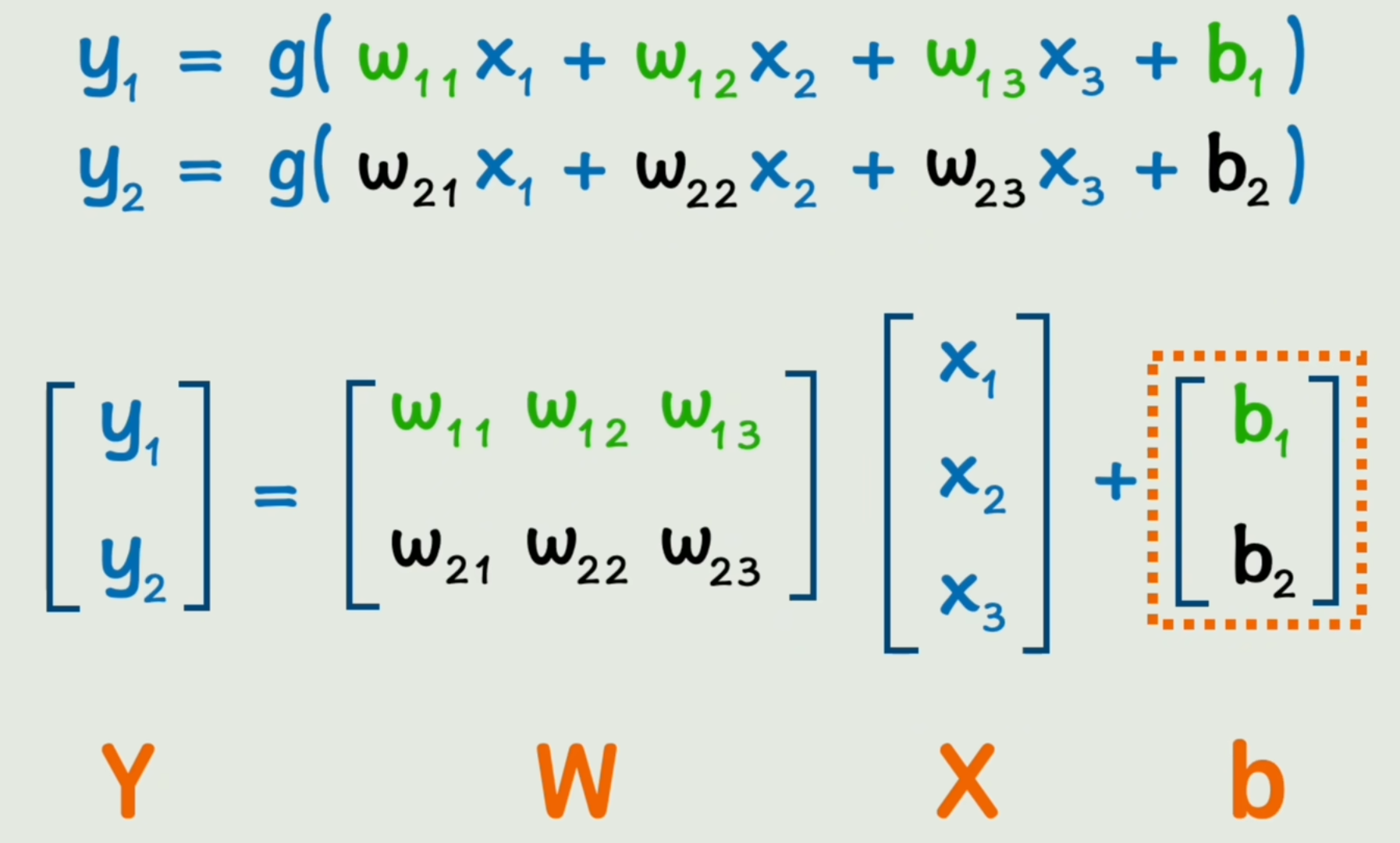
Y=g(WX+b)Y=g(WX+b) Y=g(WX+b)
但是神经网络的「层」并没有体现在公式中。
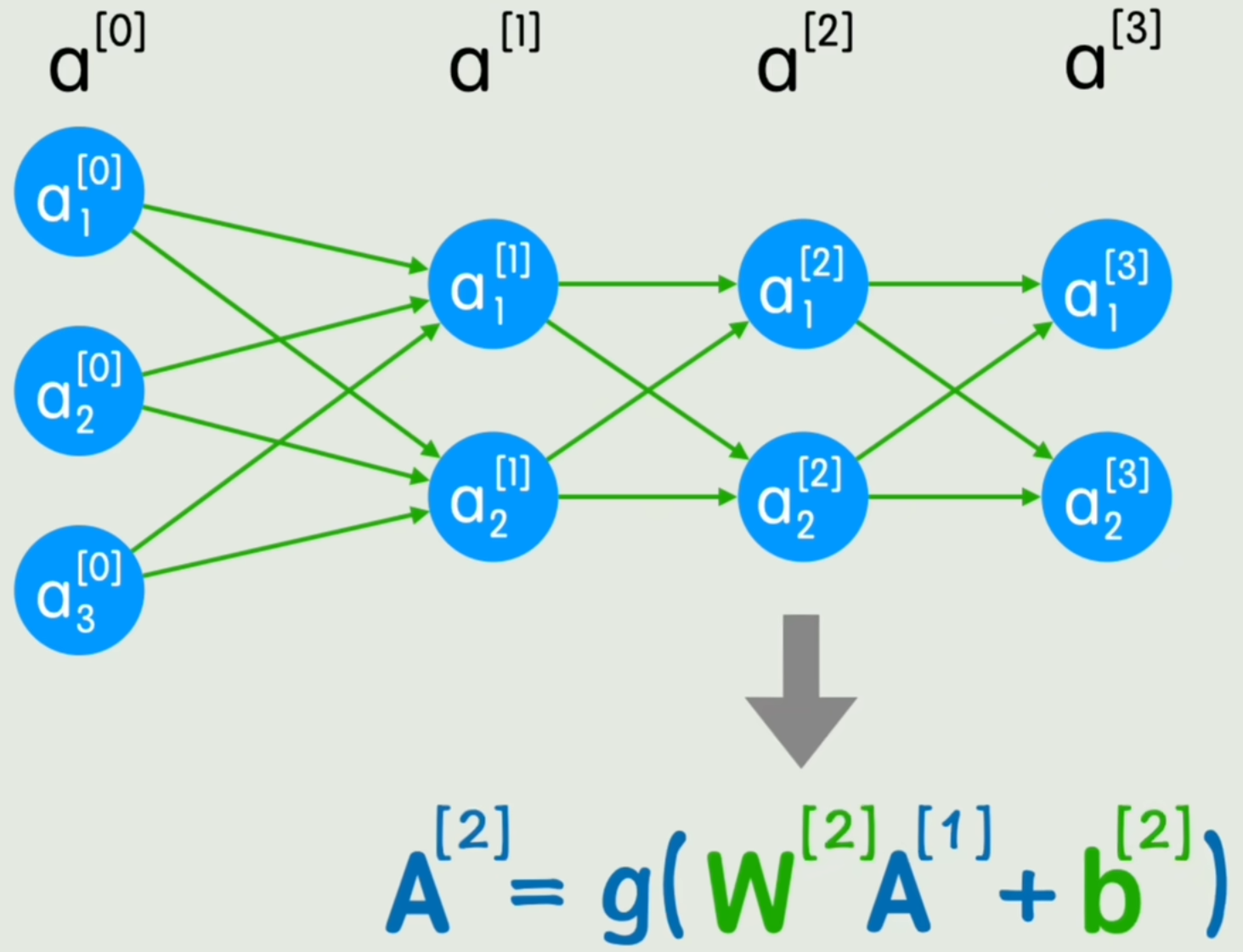
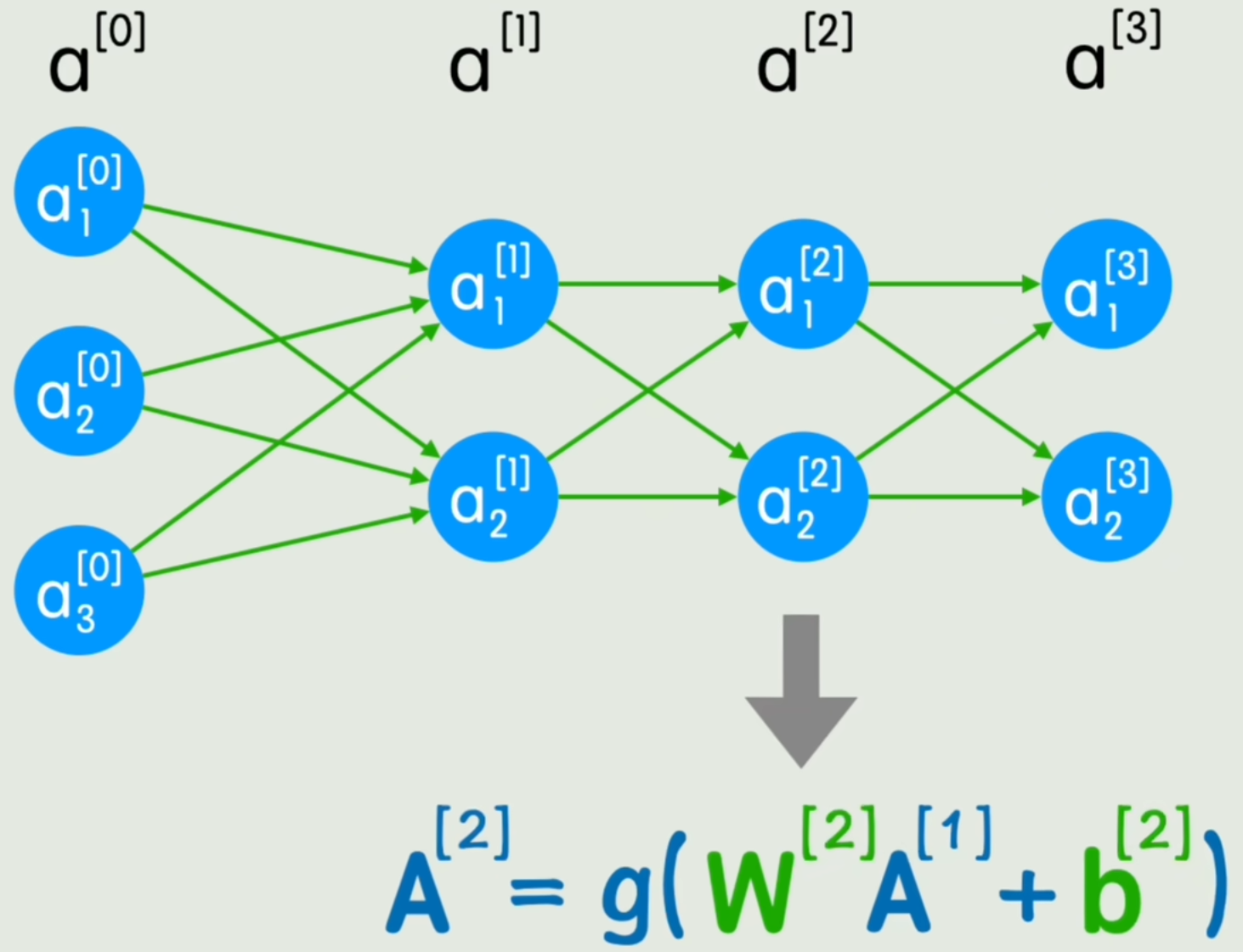
我们将x、yx、yx、y、隐藏层等通通抽象为「第aaa层」。将“第几层”用lll表示,就得到了:
A[L]=g(W[L]A[L−1]+b[L]){\color{red}A^{[L]}}=g(W^{[L]}{\color{red}A^{[L-1]}}+b^{[L]}) A[L]=g(W[L]A[L−1]+b[L])
既简化了写法,又可以利用GPU并行计算特性,加速神经网络的训练和推理过程。
全连接层&卷积核&池化层
- 全连接层
我们注意到,每个神经元「小圆圈」都与前一层所有的神经元相连接,称这样一层神经元为「全连接层(FC)」。也就是说,还有不是全连接层的「层」。
- 卷积核
全连接层的局限性,一个30x30的图片,900个输入,假设后一层有1000神经元,那么就是90万参数。
在灰度图片中找一个3x3的矩阵,与一个确定的3x3矩阵「卷积核」对应位置相乘再求和,遍历原图所得的新数值形成一个新图像,这种运算,我们称为「卷积运算」。
在传统图像处理领域,卷积核是已知的。
而在深度学习领域,卷积核的值也是参数wiw_iwi,是被训练出来的一组值。
将神经网络其中一个全连接层替换为「卷积层」,就大大减少了权重参数的数量,还能更有效的捕捉图片的局部特征,可谓一举两得。
从公式上看,将原来的矩阵叉乘替换为了卷积运算。
A[L]=g(W[L]∗A[L−1]+b[L])A^{[L]}=g(W^{[L]}{\color{red}*}A^{[L-1]}+b^{[L]}) A[L]=g(W[L]∗A[L−1]+b[L])
至此,神经网络也不用画成一个个的小圈了,而是用更简洁的方块表示。
除了卷积层外,还有「池化层」。作用是对卷积后的特征图像进行「降维」,减少计算量同时保留主要特征。
- 池化层
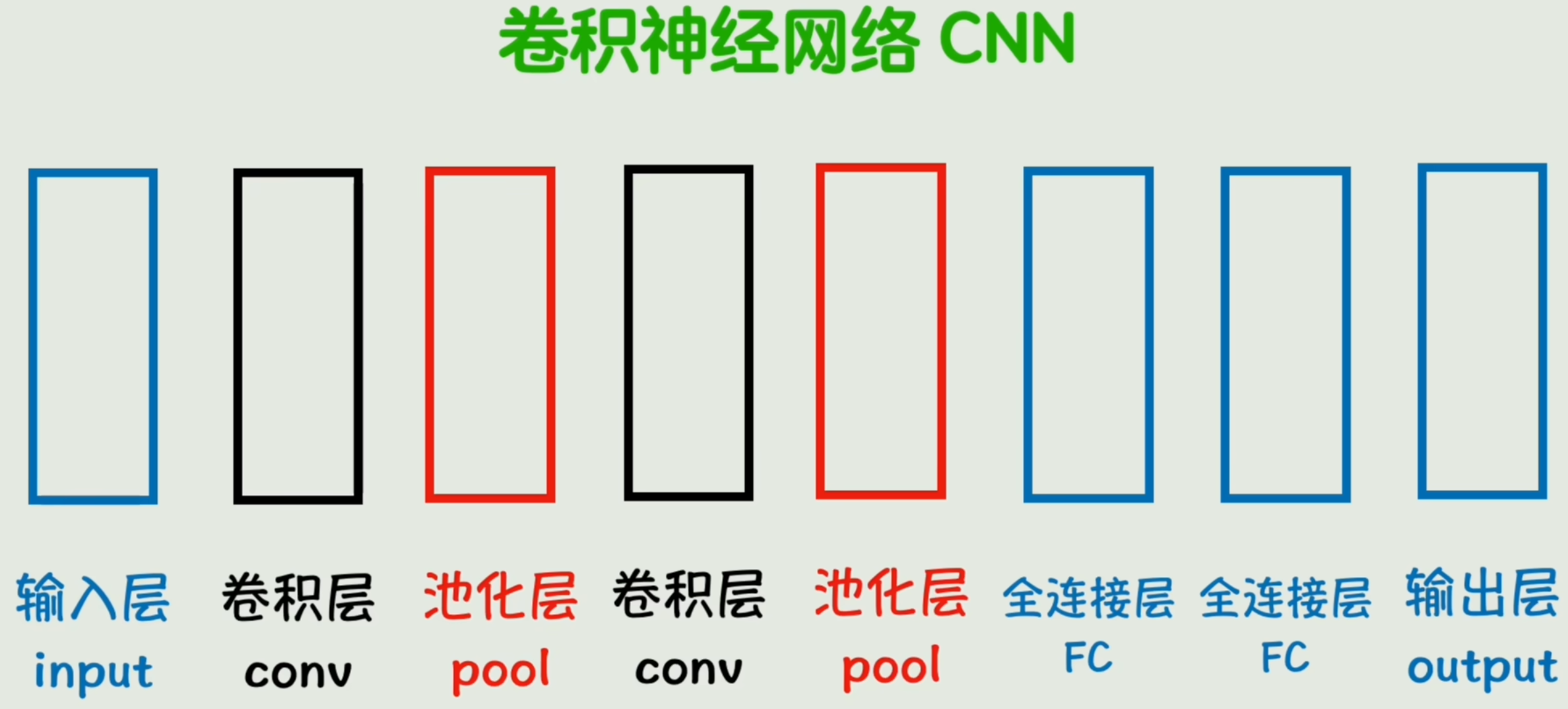
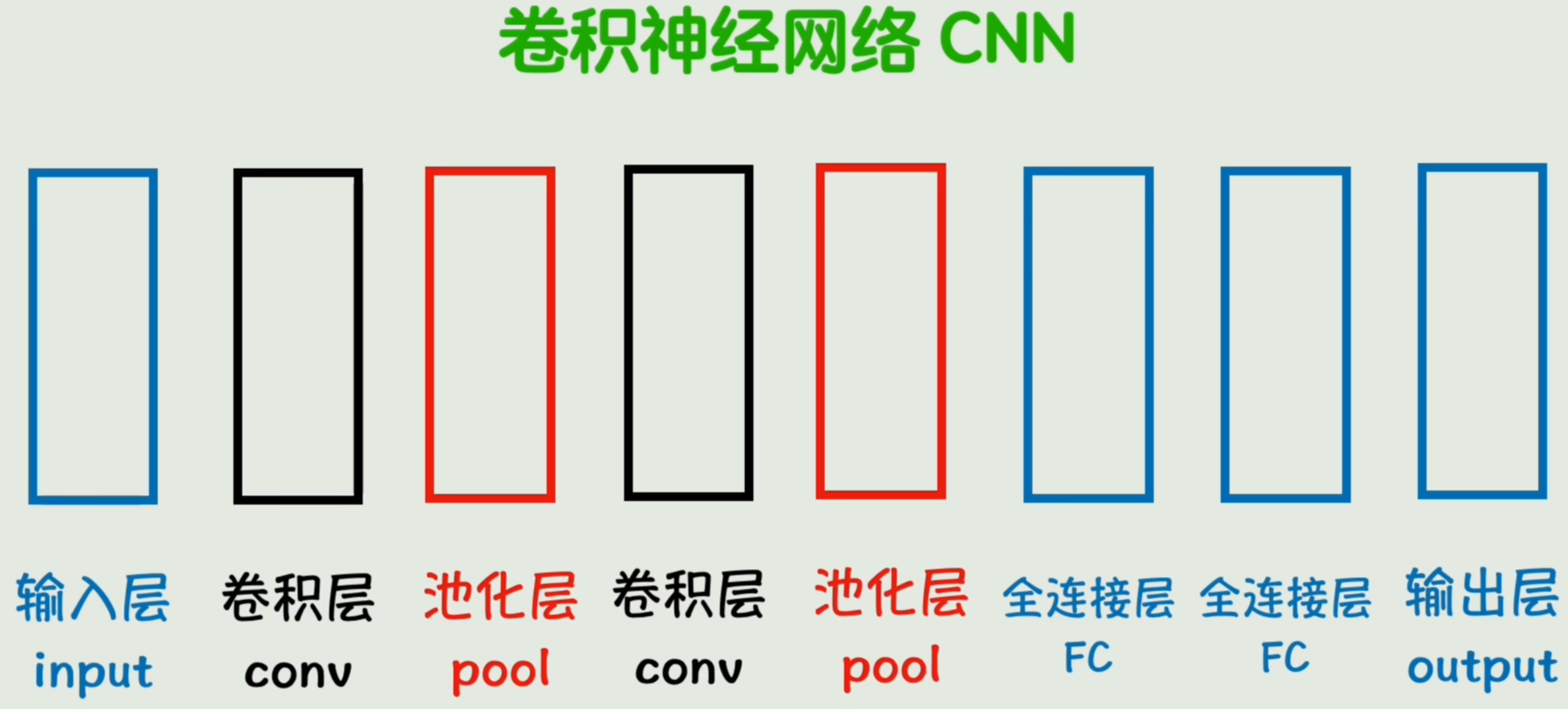
- 卷积神经网络(CNN)
「全连接层」、「卷积层」、「池化层」都可以有多个,由它们组成的适用于图像识别领域的实际网络结构,我们称为「卷积神经网络(CNN)」。
从词嵌入到RNN
词向量&词嵌入
给你几个字,让你生成后面一个字。给你一句话,然你判断每个词的褒贬。
把文字作为参数,要先把文字「编码」为计算机能识别的01数字。
- 词向量:通过词语编码得到的向量
有两种极端编码方式:
- 一个数字对应一个词语。词表大小对应数字标识范围大小。缺点非常明显:维度太低「一维向量」,且数字标识本身无法衡量词与词之间相关性。
- 准备一个超级大的向量,每个词只有向量中一个位置是1,剩余全0。这种编码方式称为「one-hot 独热编码」。缺点:维度太高,太稀疏,且每个向量都是正交的,且仍无法找到词间相关性。(若将向量中每个位置看做特征,那其特征极其死板「是不是“该词”」)
- 词嵌入 word embedding
维度太高太低都不好,那就弄个不高不低的,称为「词嵌入」,一种高效好用的编码方式。
通过词嵌入编码方式得到的词向量,维度适中。其向量的每个位置依然可以理解为某个特征值,不过该「特征值」是训练出来的,人类可能完全无法理解。
由词向量组成的矩阵,称为「嵌入矩阵」。(由经典训练方法word2vec得出)
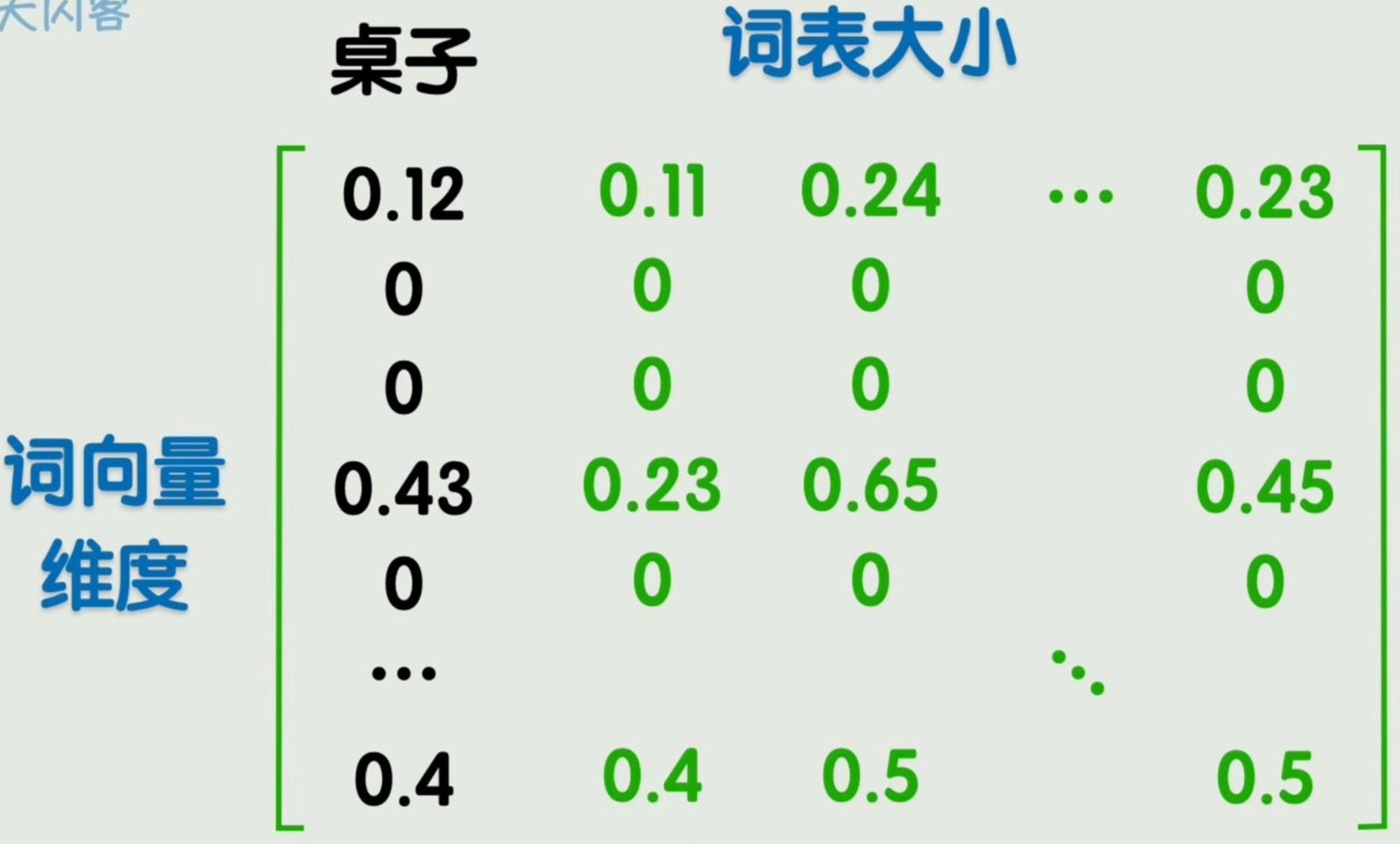
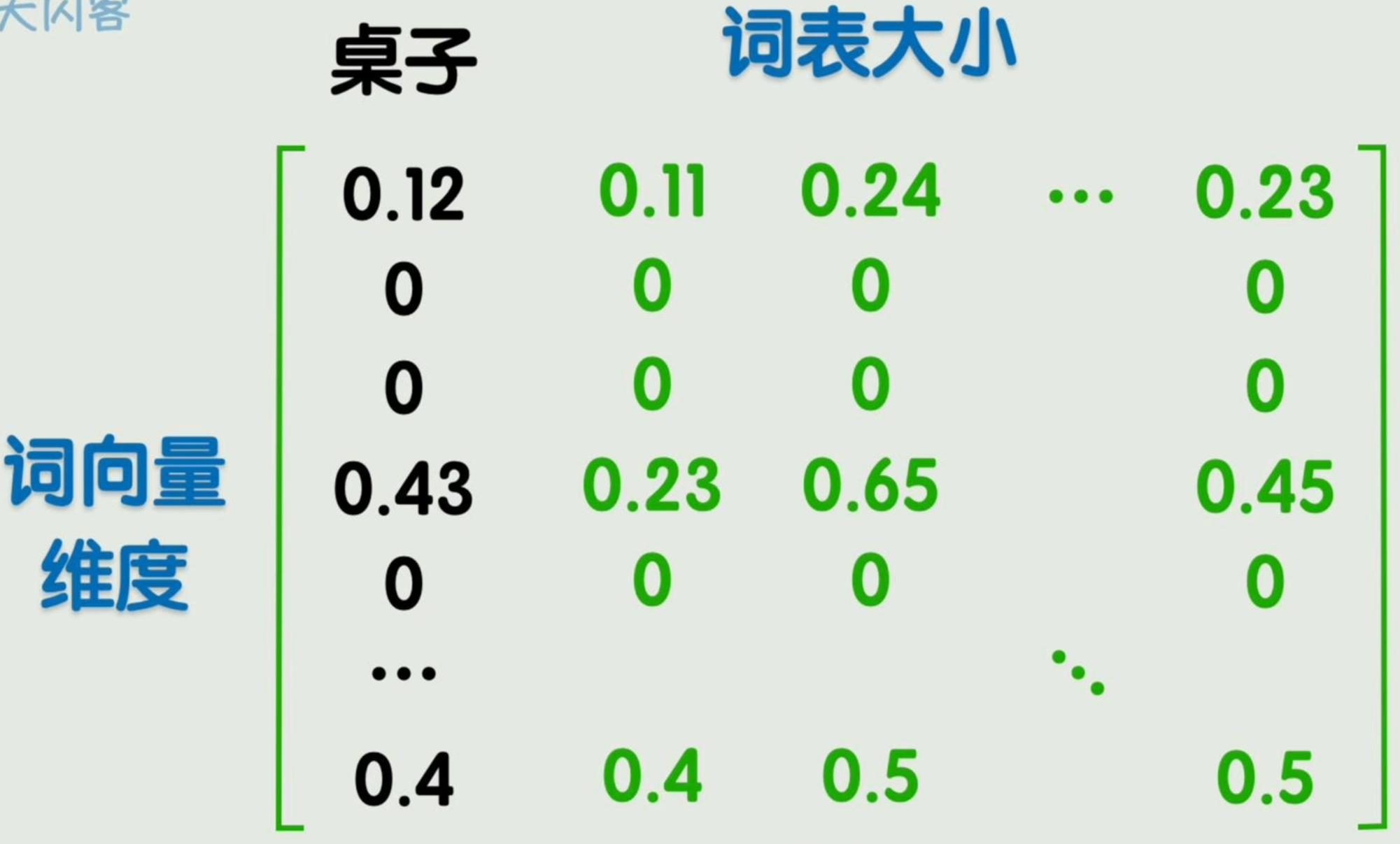
词向量维度远高于三维,因此其所在空间维度也很高,称为「潜空间」。
如何表示词间语义上的相关性呢?
向量点积&余弦相似度
- 向量点积
- 余弦相似度
a⋅b=∑i=1naibi\mathbf{a} \cdot \mathbf{b} = \sum_{i=1}^{n} a_i b_i a⋅b=i=1∑naibi
cos(θ)=a⋅b∥a∥⋅∥b∥\cos(\theta) = \frac{\mathbf{a} \cdot \mathbf{b}}{\lVert \mathbf{a} \rVert \cdot \lVert \mathbf{b} \rVert} cos(θ)=∥a∥⋅∥b∥a⋅b
通过求出向量间相关性,进而表示词语间相关性。「虽能算出但不够直观Embedding projector - visualization of high-dimensional data投射到三维,可视化观词间关系」
此时,词就可以编码为向量,送到输入端的神经元了。
假设词向量的维度是300维,那么一句五个词的话所需要的输入端神经元就是1500个。
问题来了,一是输入层太大。二是随话中词语数量变化,导致输入端是变长的。三是无法体现词间先后顺序,仅平铺开输入「类似那个30*30导致90万参数的图片,缺点很多,不可取」。
图像处理领域采用卷积来提取图像特征,自然语言处理领域如何解决词间顺序问题呢?
RNN
- RNN
经典神经网络无法表达词间先后顺序,因此我们添加一个隐藏状态,在词间传递。
我们在第一个词经过非线性变化后,先不输出结果Y1Y_1Y1,而是输出一个中间结果H1H_1H1「隐藏状态」,再经过一次非线性变换得到Y1Y_1Y1。
中间隐藏状态H1H_1H1用来加入第二个词一起参与运算,这样就达到了「传达前词信息」的目的。
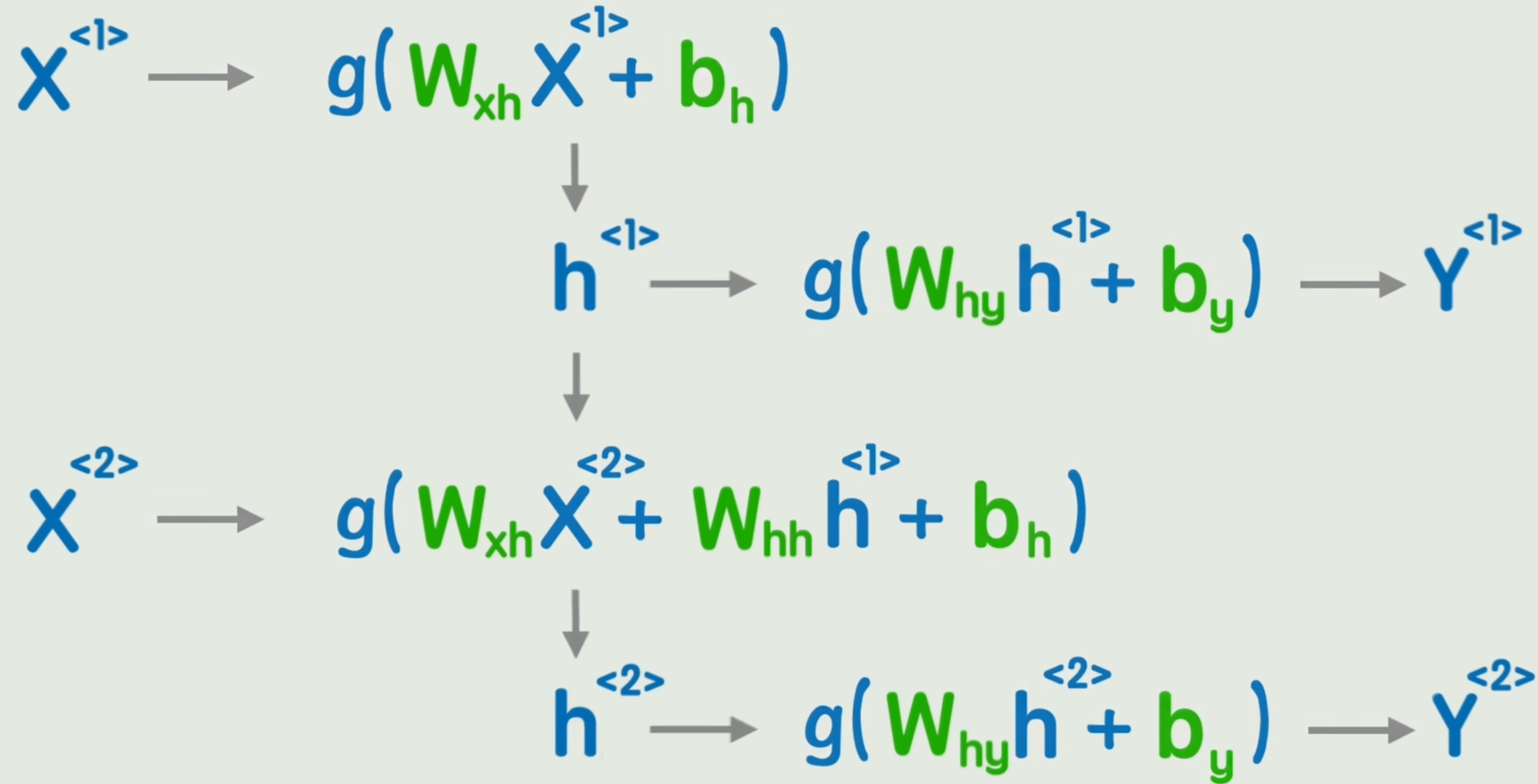
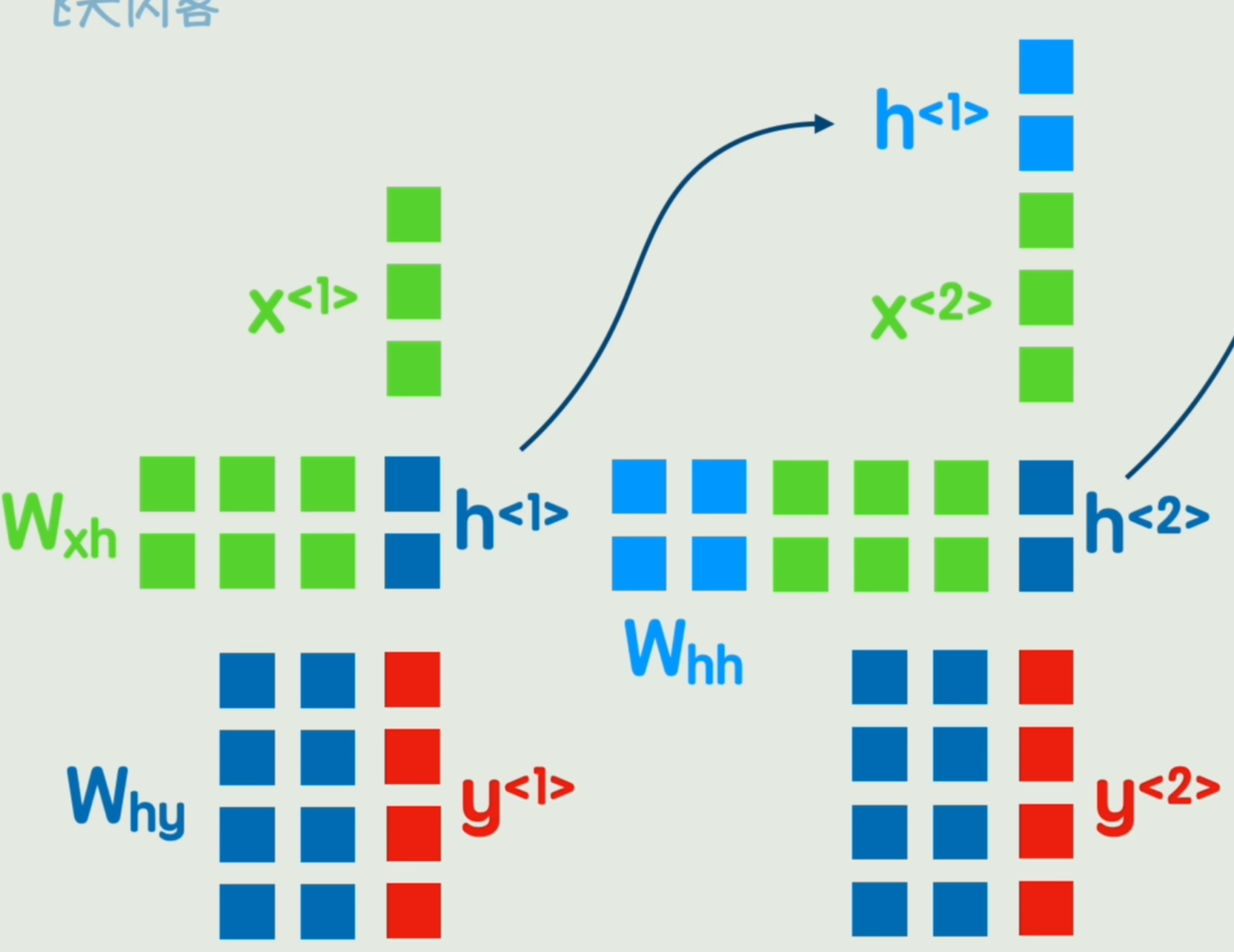
称之为「循环神经网络 RNN」,和经典神经网络相比,只是多了一个前一时刻的隐藏状态而已。
h<t>=g1(WxhX<t>+Whhh<t−1>+bh)y<t>=g2(Whyh<t>+by)h^{<t>} = g_1(W_{xh} X^{<t>} + {\color{red}W_{hh} h^{<t-1>}} + b_h)\\ y^{<t>} = g_2(W_{hy} h^{<t>} + b_y) h<t>=g1(WxhX<t>+Whhh<t−1>+bh)y<t>=g2(Whyh<t>+by)
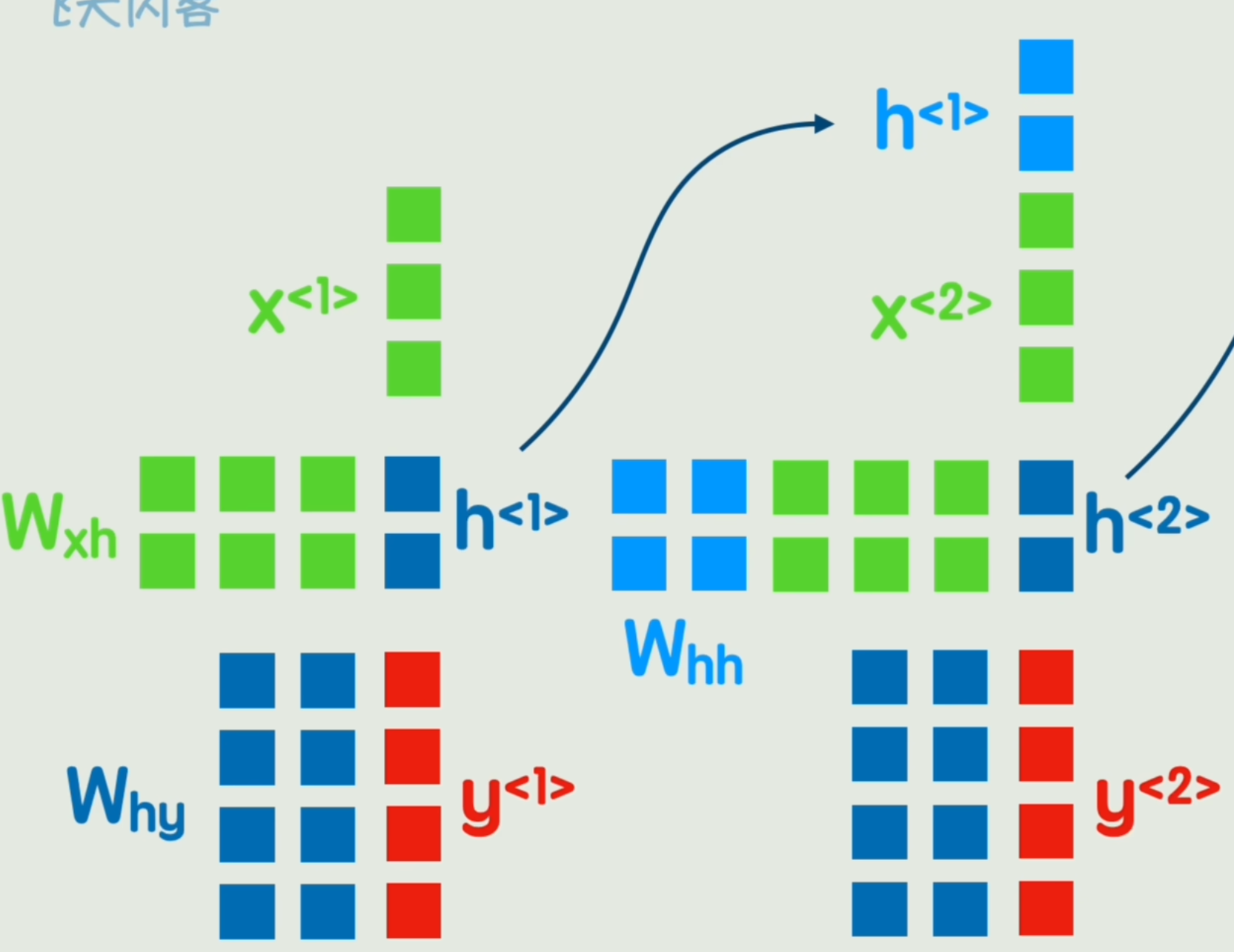
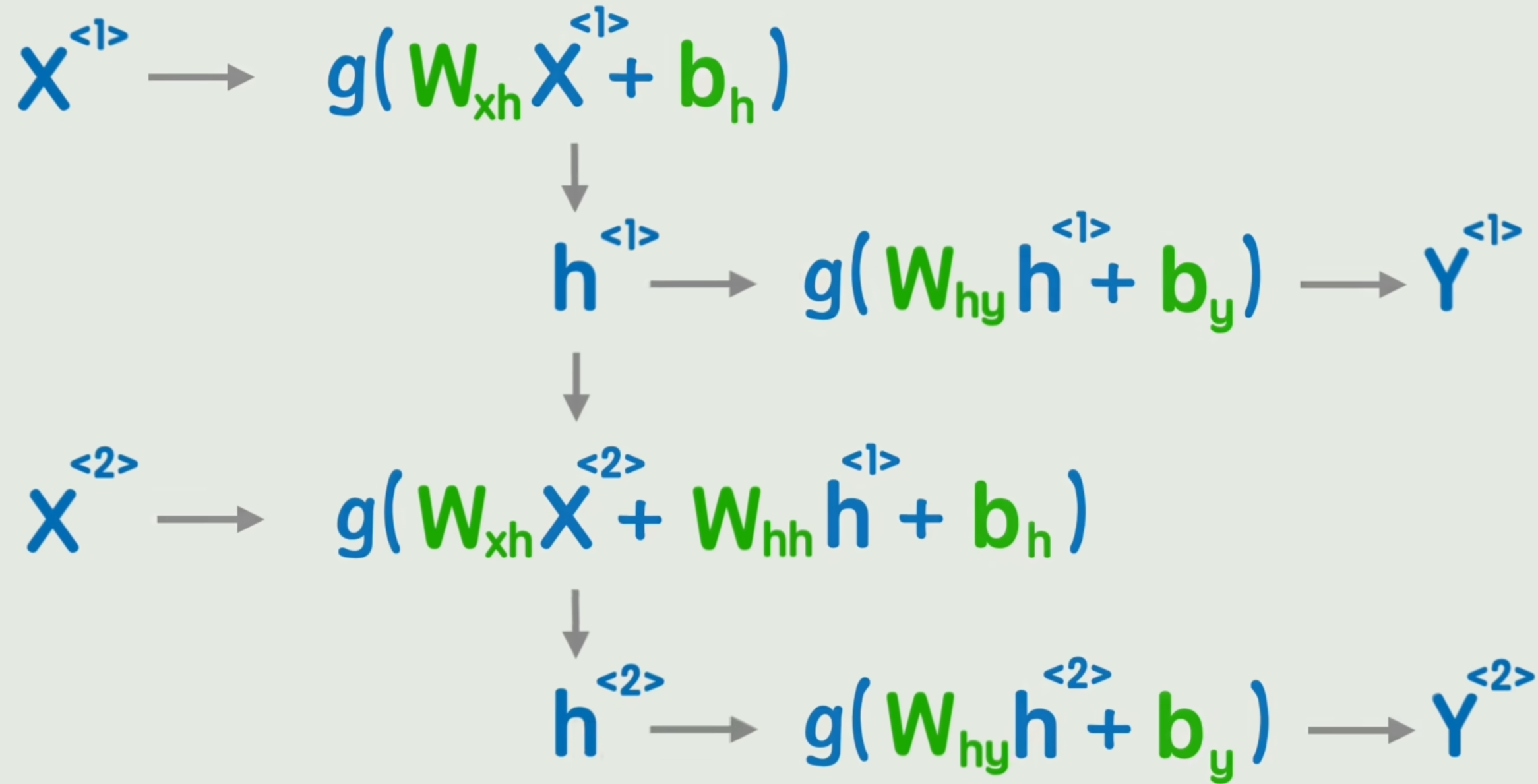
可以看出,RNN有两个严重问题:
- 无法捕捉长期依赖「信息随时间步增多逐渐丢失」
- 无法并行计算「必需按序处理」
为了解决问题,人们引入了GRU和LSTM「只能缓解无法根治,已过时」。
那么我们是否有一种可以彻底抛弃顺序计算,直接一眼把全部信息尽收眼底的新方案呢?
- 恭迎 TRANSFORMER!


简单而强大的Transformer
线性映射
- 线性映射:注意力前置条件
首先,我们给每个词向量加一个「位置编码」,表示词在句中的位置。得到一个含有位置信息的词向量。
此时,词还注意不到其他词的存在。
我们用三个矩阵Wq、Wk、WvW_q、W_k、W_vWq、Wk、Wv「训练出来的」分别与第一个词向量相乘,得到三个向量q1、k1、v1q_1、k_1、v_1q1、k1、v1,对其他词向量也做相同运算。
将所有向量的q、k、vq、k、vq、k、v拼成矩阵Q、K、VQ、K、VQ、K、V「实际运算时直接矩阵相乘得到」。
qi=Wqxiki=Wkxivi=WvxiQ=[q1Tq2T⋮qnT]=Wq[x1Tx2T⋮xnT]=WqX% 单个词向量生成q、k、v {\color{red}\mathbf{q}_i} = \mathbf{W}_q \mathbf{x}_i \\ {\color{red}\mathbf{k}_i} = \mathbf{W}_k \mathbf{x}_i \\ {\color{red}\mathbf{v}_i} = \mathbf{W}_v \mathbf{x}_i \\ % 矩阵形式(拼接所有词向量的q、k、v) \mathbf{Q} = \begin{bmatrix} \mathbf{q}_1^T \\ \mathbf{q}_2^T \\ \vdots \\ \mathbf{q}_n^T \end{bmatrix} = \mathbf{W}_q \begin{bmatrix} \mathbf{x}_1^T \\ \mathbf{x}_2^T \\ \vdots \\ \mathbf{x}_n^T \end{bmatrix} = \mathbf{W}_q \mathbf{X} \\ qi=Wqxiki=Wkxivi=WvxiQ=q1Tq2T⋮qnT=Wqx1Tx2T⋮xnT=WqX
注意力!
- Attention!注意力
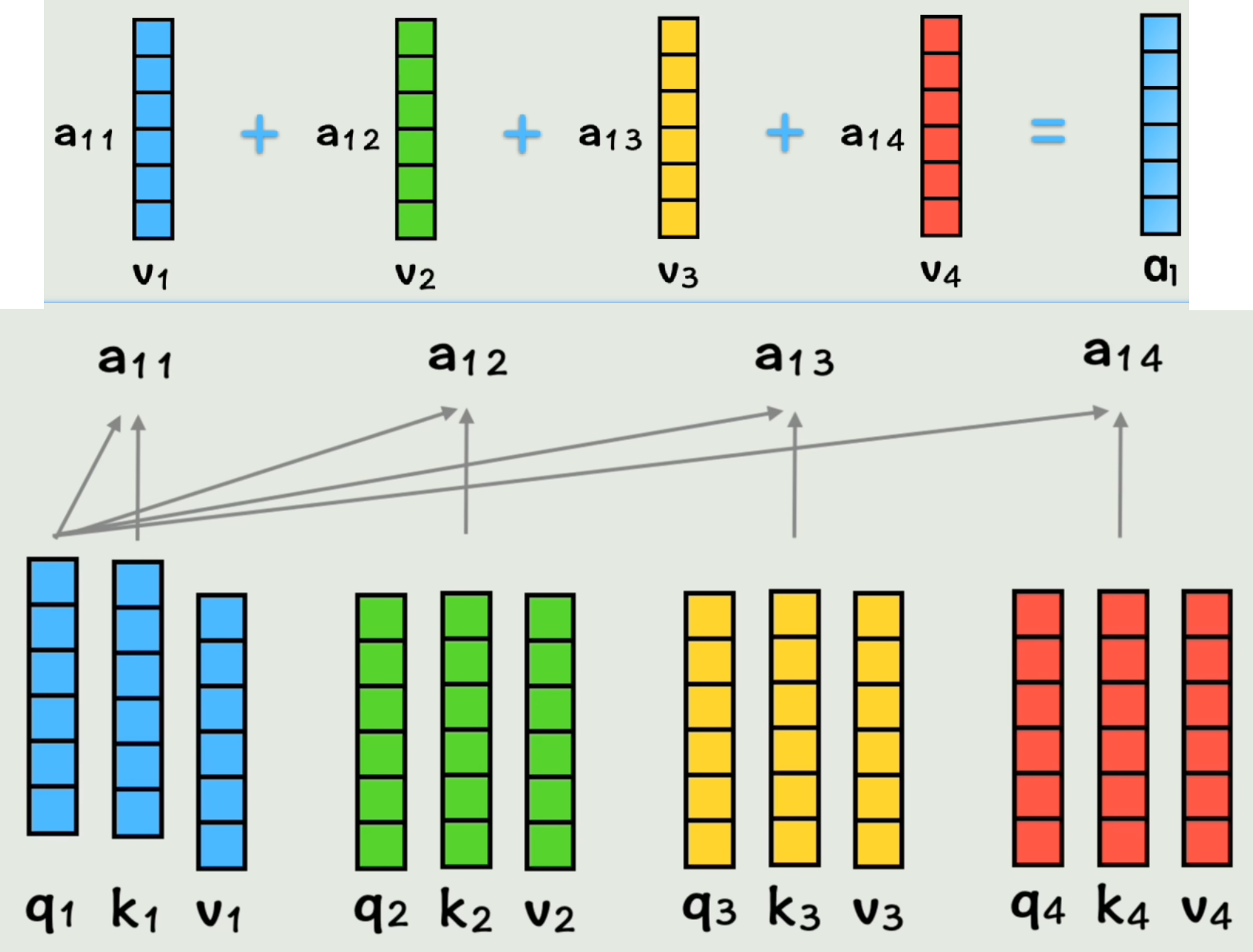
接下来让q1与k2q_1与k_2q1与k2做点积得到系数a12a_{12}a12,表示「在第一个词的视角下,第一个词和第二个词的相似度」。
同理得到系数a13、a14、a11a_{13}、a_{14}、a_{11}a13、a14、a11。
然后将系数分别与各词的vvv向量相乘再相加,得到向量a1a_1a1。表示「在第一个词视角下,按照和它相似度权重,将所有词向量加为一个整体」(包含了全部上下文信息的第一个词的新向量)。【有点类似基因】
同理,其余词得到自己的新词向量a2、a3、a4a_2、a_3、a_4a2、a3、a4「完成了包含自己位置信息和其他词上下文信息的壮举」。
a1j=q1⋅kj(j=1,2,3,4)a1=∑j=14a1j⋅vj系数矩阵A=Q⋅K⊤a=A⋅V% 相似度系数计算(以第一个词视角为例) a_{1j} = \mathbf{q}_1 \cdot \mathbf{k}_j \quad (j = 1, 2, 3, 4)\\ % 第一个词的上下文向量(未归一化版本) \mathbf{a}_1 = \sum_{j=1}^{4} a_{1j} \cdot \mathbf{v}_j\\ % 矩阵形式(批量计算) 系数矩阵A = \mathbf{Q} \cdot \mathbf{K}^\top\\ \mathbf{a} = A \cdot \mathbf{V} a1j=q1⋅kj(j=1,2,3,4)a1=j=1∑4a1j⋅vj系数矩阵A=Q⋅K⊤a=A⋅V
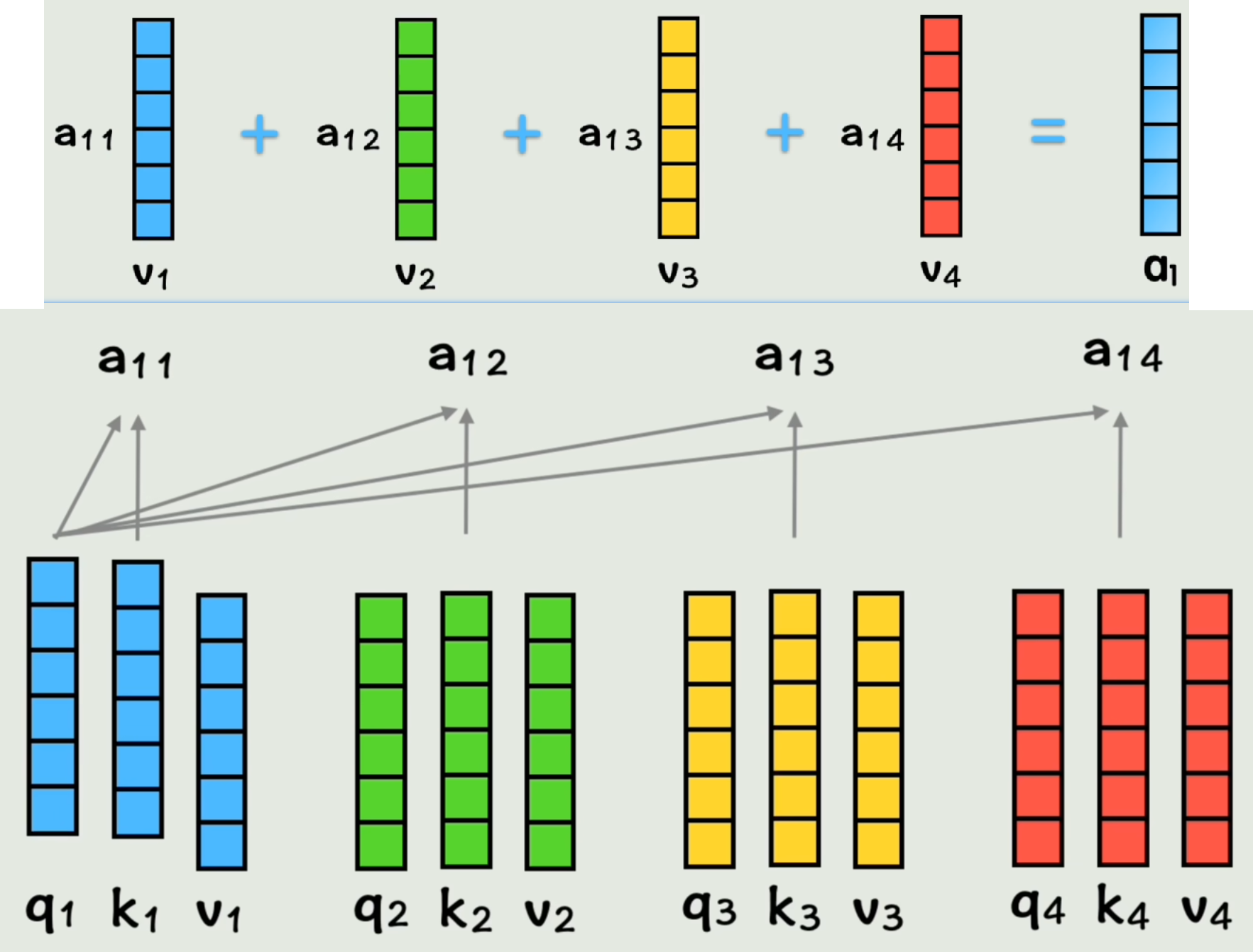
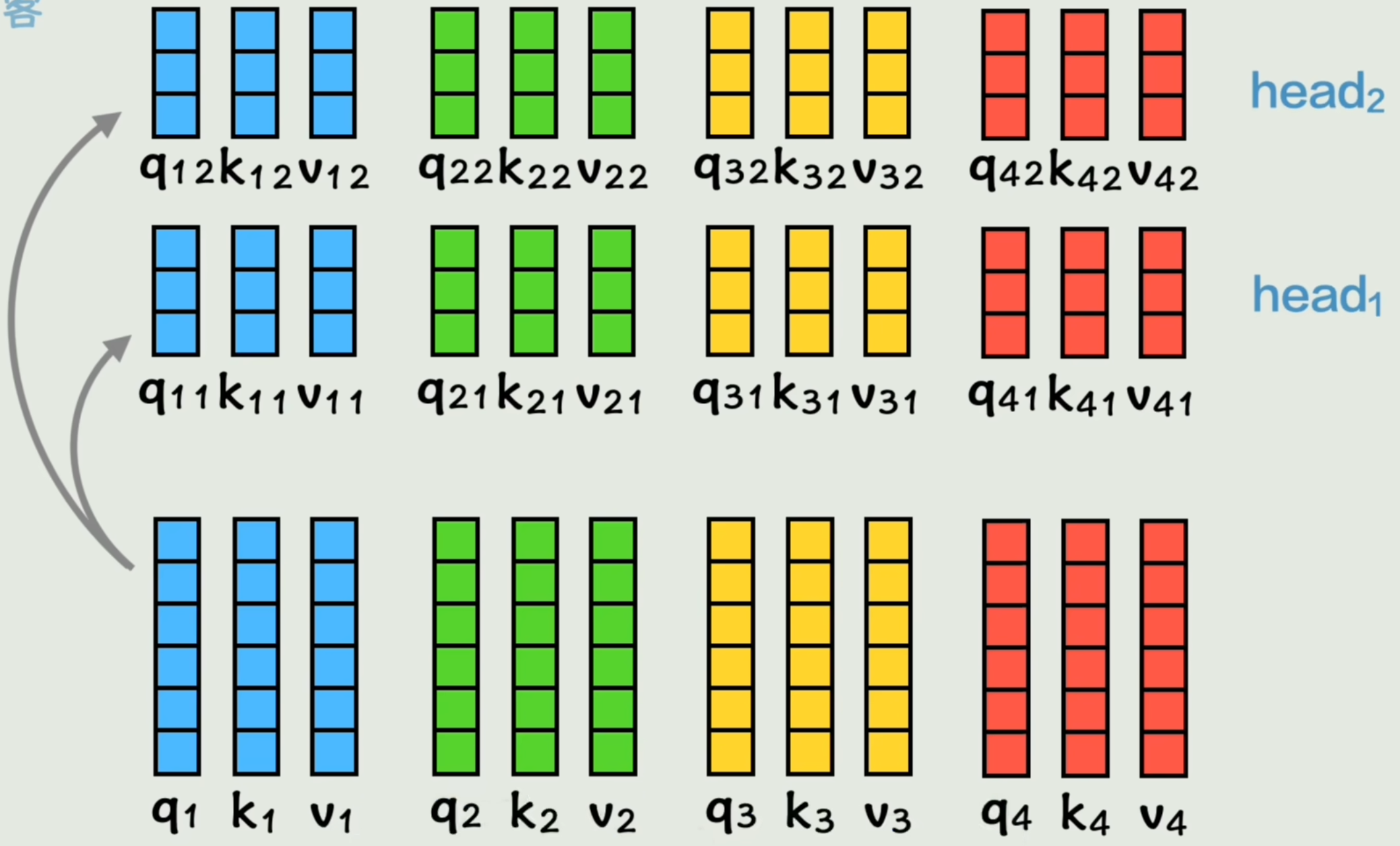
- 多头注意力
之前的前置工作是制作了一组QKV矩阵,现在我们用两组W权重矩阵计算出两组QKV,称之为「Head 头」。
给每个词两组学习上下文机会。即「两头注意力」。
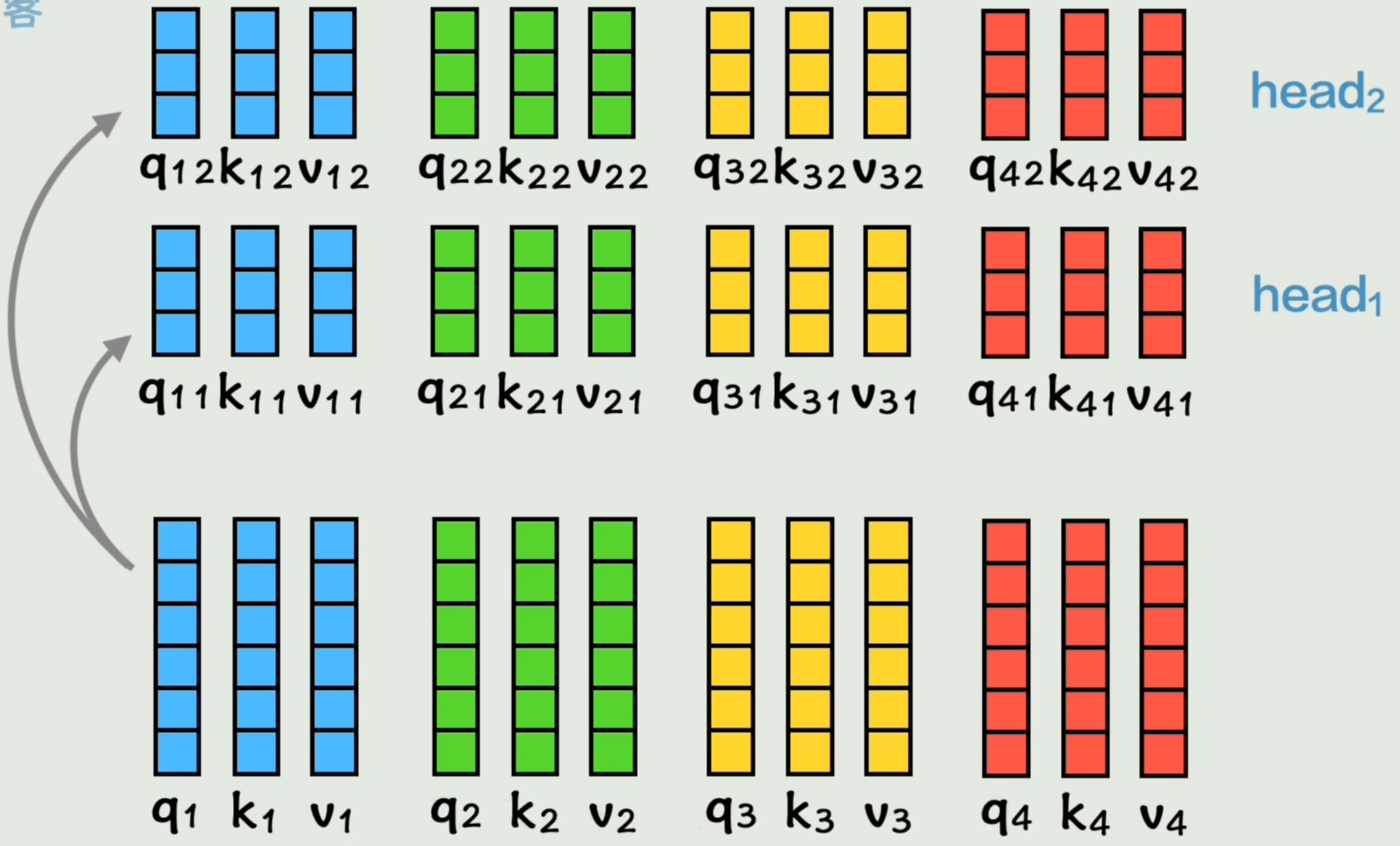
经过「注意力」运算后得到a1h1a_{1h_1}a1h1和a1h2a_{1h_2}a1h2,拼接成全新的a1a_{1}a1。「并非简单拼接,还经过了一次线性变换」
- transformer
Attention(Q,K,V)=softmax(QKTdk)V\text{Attention}(Q, K, V) = \text{softmax}\left( \frac{QK^T}{\sqrt{d_k}} \right) V Attention(Q,K,V)=softmax(dkQKT)V
MultiHead(Q,K,V)=Concat(head1,…,headh)WOwhere headi=Attention(QWiQ,KWiK,VWiV)\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, \ldots, \text{head}_h) W^O \\ \text{where } \text{head}_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V) MultiHead(Q,K,V)=Concat(head1,…,headh)WOwhere headi=Attention(QWiQ,KWiK,VWiV)
引用
【一小时从函数到Transformer!一路大白话彻底理解AI原理】https://www.bilibili.com/video/BV1NCgVzoEG9?p=4&vd_source=cce88d7fe1e543210d68fa276e5b4dd4
