TREE SEARCH FOR LLM AGENT REINFORCEMENTLEARNING
目录
目前RL存在两个key challenges:
本文动机:
问题抽象:
具体过程:
更少的预算:
Tree-based group relative advantages
tree-based credit:
一、计算核心差异:分组范围决定基线来源
1. intra-tree(树内)优势估计
2. inter-tree(树间)优势估计
二、“差比” 关联:互补结合形成最终优势
IMPLICIT STEP-LEVEL PREFERENCE LEARNING
实验:
不同训练预算下的表现
拆解 1:为什么单轮场景中,“多轨迹优势” 会减弱?
拆解 2:为什么多轮场景中,“细粒度过程监督收益” 会保留?
链式与树式方法的超越性能表现。
目前RL存在两个key challenges:
1. sample multiple independent trajectories for each task in a chain-based rollout scheme
2. Sparse supervision in long-horizon, multi-turn trajectories
本文动机:
Can we construct more fine-grained supervision signals for agent RL
under a limited rollout budget while still solely based on outcome rewards?(使用更少的预算,提供更丰富的rewards)
为了解决稀疏监督的难题,通过树结构估计相对优势,构建更细粒度的过程监督信号。在树的每个分支点,从各个子树的叶节点反向传播结果奖励,子树的深度决定了过程监督的粒度。树搜索策略采样随机扩展,天生产生不同粒度的过程信号,让模型能够学习中间决策。
问题抽象:
具体而言,在每一个时间步 t = 0,1,...,T−1,大型语言模型(LLM)都会基于现有上下文状态 st 生成一个思考过程 τt 和一个可解析的文本动作 αt。该动作通常对应于工具的使用,智能体通过这一动作与环境进行动态交互,从而获得新的观察结果 ot。一个完整的 T 步智能体回合包含三条交织的轨迹:
![]()
此类动态过程可描述为一个马尔可夫决策过程(Markov Decision Process,MDP),记为 M = {S, A, P}。其中:
- S 代表状态(state),即截至某一时间步 H<t 的完整交互上下文;
- A 代表复合动作空间(compound action space),每个动作包含一个 “思考 - 行动” 对(τₜ, αₜ);
- P 代表转移动态(transition dynamics),既包含外部环境的转移(Pₑₙᵥ),也包含不同时间步完整上下文的拼接。
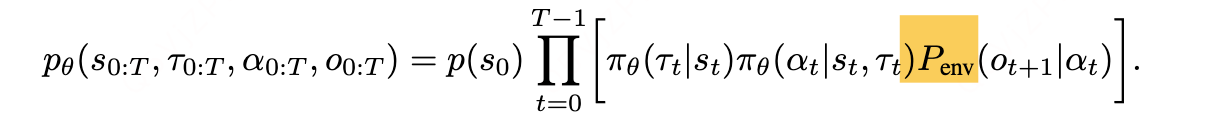
具体过程:
- 初始化(Initialization):对于每个提示 xi,我们首先通过策略模型 πθ 生成 M 条独立的基于链结构的轨迹 Y = {Hi ∼ πθ(・|xi)} M,将其作为 M 棵树 T 的初始化内容。
- 采样(Sampling):之后从每棵树 Ti 中,排除叶节点(智能体答案,agent answer),随机采样 N 个节点,(每个node代表一个tuple(
))得到节点集合 Pi = {pi,j ∈ Ti} N,用于后续扩展。
- 扩展(Expansion):对于每个选中的节点 pi,j,我们将 “从根节点到该节点的完整上下文”(记为 Hi<t = {proot i,j ,..., pfather i,j , pi,j})与原始提示 xi 共同作为输入,通过策略模型继续生成响应的剩余部分(记为 Ynew = {Hi≥t ∼ πθ(・|xi, Hi<t)} N),随后将该部分作为新分支插入原树,即通过 Ti ← Ti ∪ Ynew 完成树的更新。
更少的预算:
通过迭代重复步骤 2 和步骤 3 共 L 次,该树搜索过程最终会为单个提示生成总数为 M×(L×N+1) 的轨迹(rollout),并将此作为最终分组规模 G。这些轨迹均匀分布在 M 棵树中。
设单条智能体轨迹的期望轨迹预算(包含词元数和工具调用次数)为 B。在每次随机树扩展中,所选节点的期望深度为最大深度的一半,相应的期望成本为 B/2。这意味着在相同的词元 / 工具调用预算下,使用树搜索可获得更多用于训练的智能体轨迹。
具体而言,树搜索采样的总期望预算由以下公式确定:
E[Btree] = M·B + L·N·B/2. (4)
第一项为树初始化的budget,第二项为进行探索所需budget的期望值( B/2是因为共享相同的前缀,节省下来的budget)
在固定采样预算下,减少树的数量 M、同时增加扩展次数 N 和迭代次数 L,虽能提升轨迹数量,但也会缩小探索范围 —— 因为更多轨迹会共享相同的前缀。在我们的实验中,不同的树结构配置(tree configuration)展现出了不同的效果。
Tree-based group relative advantages
因此优势估计(advantage estimation)也处于轨迹级。这意味着,包含多步骤的整个多轮智能体轨迹会被赋予相同的信用(credit),具体表示为:
A(H) = A({(τ0,α0,o0),…,(τT,αT,oT)}) = A({τ0,α0,o0}) = … = A({τT,αT,oT}) (5)
由于这种粗糙的信用分配(credit assignment),此类稀疏奖励(sparse rewards)会严重影响长周期(long-horizon)多轮智能体强化学习训练的稳定性。
tree-based credit:
在 Tree-GRPO 中,intra-tree(树内)优势估计与inter-tree(树间)优势估计的核心差异体现在分组范围和计算基线上,两者的互补性是为了平衡 “过程监督的细粒度” 与 “基线估计的稳定性”。具体计算差异和关联如下:
一、计算核心差异:分组范围决定基线来源
两种优势估计的计算公式结构一致(均为标准化的奖励偏差),但分组的轨迹集合完全不同,导致基线(均值和标准差的计算基础)存在本质差异:
1. intra-tree(树内)优势估计
- 分组范围:仅包含单棵树(Ti)内部的所有轨迹(G_intra-tree (Ti))。这些轨迹共享部分前缀(因树结构的分支特性),属于 “同源扩展的轨迹簇”。
- 计算逻辑:以同一棵树内的轨迹为基线,衡量当前轨迹 Hi 在 “同源子树” 中的相对优势:
其中,分子是当前轨迹奖励与 “树内所有轨迹的平均奖励” 的偏差,分母是树内奖励的标准差(标准化处理)。
- 核心作用:利用树内轨迹的 “共享前缀” 特性,捕捉细粒度的过程级信号(如同一分支点下不同子树的奖励差异),反映 “局部决策(如某一步思考 - 行动)对结果的影响”。
2. inter-tree(树间)优势估计
- 分组范围:包含所有树(所有 Ti)的轨迹(G_inter-tree,即跨树的全局轨迹集合)。这些轨迹来自不同的初始树,前缀共享度低,属于 “异源独立的轨迹簇”。
- 计算逻辑:以所有树的轨迹为基线,衡量当前轨迹 Hi 在 “全局轨迹” 中的相对优势:
分子是当前轨迹奖励与 “所有树轨迹的平均奖励” 的偏差,分母是全局奖励的标准差。
- 核心作用:利用跨树轨迹的 “独立性”,提供更稳定的全局基线,弥补单棵树内轨迹数量少(可能导致基线估计噪声大)的问题,增强优势估计的可靠性。
二、“差比” 关联:互补结合形成最终优势
两种优势估计并非对立,而是通过直接相加形成最终的树基优势估计(见公式 7):
这种 “差比” 关系的本质是局部信号与全局基线的互补:
- intra-tree 提供 “细粒度的过程监督”(依赖树结构的分支差异),但受限于单棵树的样本量,可能存在偏差;
- inter-tree 提供 “全局稳定的基线”(依赖多树的样本量),但缺乏过程级的局部差异信号;
- 两者相加后,既保留了树结构带来的过程级信用分配优势,又通过全局基线降低了估计噪声,最终提升强化学习训练的稳定性。
IMPLICIT STEP-LEVEL PREFERENCE LEARNING
论文展示了intra-tree GRPO与step-level DPO相同的梯度结构,只有权重项不同。
实验:
不同训练预算下的表现
在大语言模型(LLM)智能体强化学习(agent RL)训练中,多轮交互产生的词元 / 工具调用成本是需要重点关注的问题。本文在不同成本约束下对所提方法进行了评估。
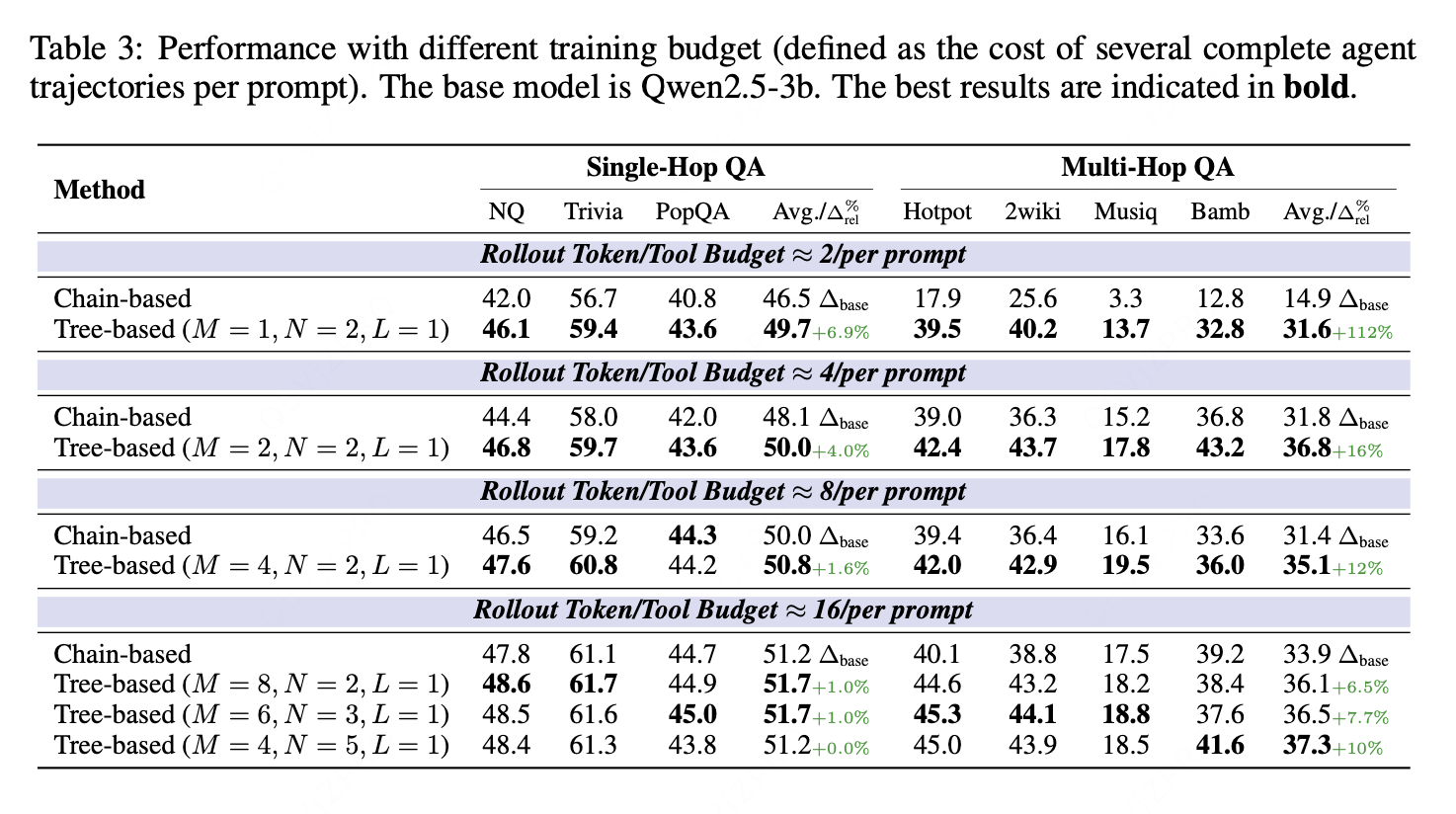
如表 3 所示,在不同预算设置下,基于树结构的方法始终展现出性能提升。尤其在轨迹生成预算高度受限的情况下(例如,每个提示仅分配生成两条完整轨迹的预算),基于链结构的强化学习难以学习多轮交互模式,而基于树结构的方法则取得了显著更优的结果(112% 的相对提升)。
随着轨迹生成预算增加,在单轮场景(single-hop setting)中,基于树结构的方法因拥有更多训练轨迹而具备的优势逐渐减弱;但在多轮场景(multi-hop setting)中,更细粒度过程监督信号带来的收益仍得以保留。值得注意的是,我们提出的 Tree-GRPO 仅使用四分之一的轨迹生成预算,性能便超过了基于链结构的方法。此外,当轨迹生成预算较高时,基于树结构的采样在参数选择上拥有更高的灵活性。
拆解 1:为什么单轮场景中,“多轨迹优势” 会减弱?
Tree-GRPO 在预算有限时,比 “链结构方法” 的核心优势之一是:能靠 “共享前缀” 生成更多轨迹(比如同样预算下,链结构能生成 2 条轨迹,树结构能生成 3 条)。
但当预算足够多(比如能生成 100 条轨迹)时,“链结构方法” 也能轻松生成 100 条轨迹 —— 这时候,Tree-GRPO “比对方多几条轨迹” 的优势就没用了。因为单轮任务太简单,“有足够多的训练数据” 就够了,不管是树结构还是链结构,只要数据量到位,性能差距会缩小,所以 Tree-GRPO “靠多轨迹提性能” 的优势自然就减弱了。
拆解 2:为什么多轮场景中,“细粒度过程监督收益” 会保留?
多轮任务的核心痛点不是 “数据不够”,而是 “不知道哪一步重要”—— 比如解数学题错了,到底是 “第一步括号算错” 还是 “最后一步加法算错”?这需要 “过程级信号” 来定位(也就是把最终奖励分到每一步)。
Tree-GRPO 的 “细粒度过程监督” 正好解决这个问题:它能通过树的分支点,把最终奖励反向传播到每一步(比如 “某分支的第一步算对了,后续奖励更高”),让模型明确 “哪一步做得好、哪一步要优化”。
而 “链结构方法” 只有 “轨迹级奖励”(比如整道题对了给 1 分、错了给 0 分),没法定位中间步骤的问题 —— 哪怕预算再多、生成再多轨迹,也解决不了 “不知道哪一步错” 的核心痛点。
链式与树式方法的超越性能表现。
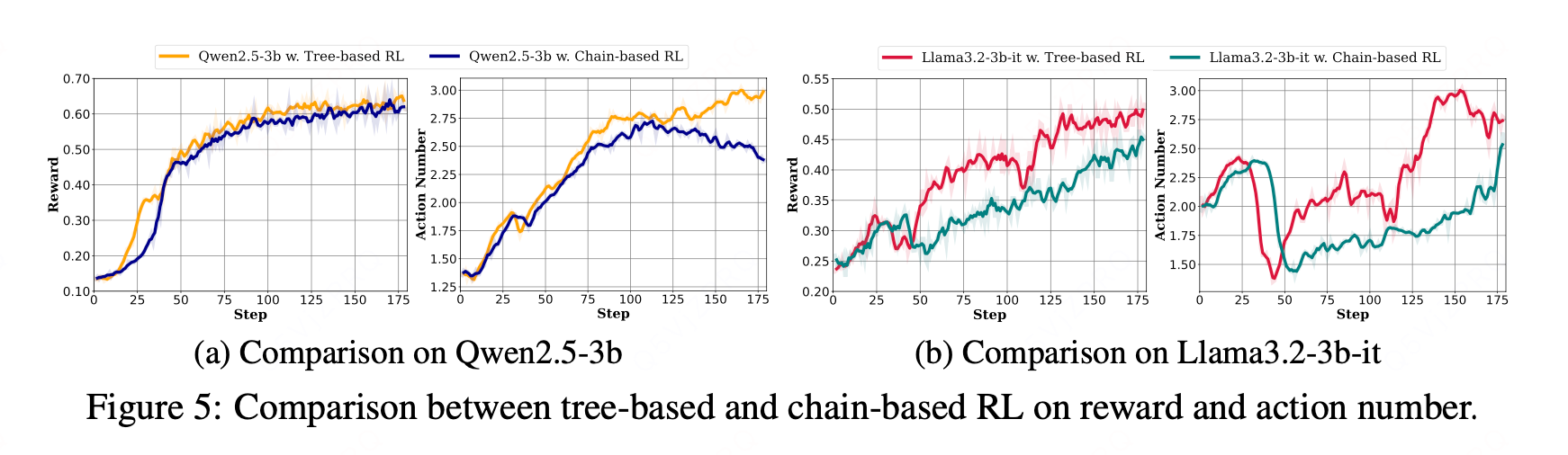
在图5的多跳问答实验中发现,除了训练奖励方面的性能提升外,基于树的方法还鼓励LLM智能体进行更长的交互(即使用更多工具调用),解决每个多跳问题的平均调用次数从2.4次增加到3.0次。这对于训练能够解决更复杂长期任务的智能体尤为关键。
此外,我们观察到学习率预热是训练30亿参数以下小模型时特别敏感的超参数。图6的结果表明,在所有学习率预热比例设置下,我们的基于树的方法均优于基于链的方法。
