Kruskal 算法深入

$Kruskal$ 算法

一、前言

终于开启了图的算法的旅程~有请第一个算法——$Kruskal$ 算法，

二、$Kruskal$算法

2.1 导入——最小生成树

2.1.1 定义

生活中，如果我们要在几个城市之间建立通路，最根本的目标是：用料最少，路径最短。这种情况该如何做呢？

不知道你有没有想到图的概述中的极小连通子图的概念。
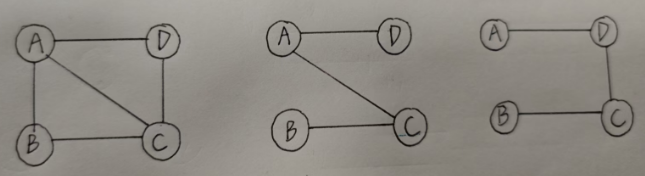
如图：

最左边图旁边的都是其的极小连通子图（还能画出好几种），以这种方式变现出来的路径都很短。但当给不同的边加上权值（路的成本），那究竟哪个是最好的选择呢？这就有了最小生成树的概念。

最小生成树可是和树结构没有一点关系的哦~

在含有n个顶点的连通图中选择n - 1条边，构成一棵极小连通子图，并使该连通子图中n - 1条边上权值之和达到最小，则称其为连通图的最小生成树。

如图：

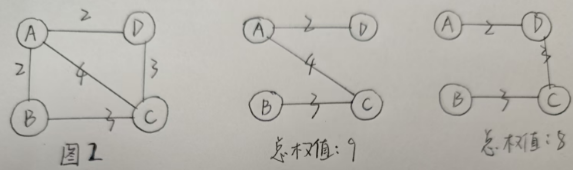
注意：最小生成树结构不是唯一的哦~在找最小生成树时有两个算法：$Kruskal$算法和$Prim$算法，对于同一个图，找最小生成树的结果可能不同。

2.1.2 生成树的属性

• 一个连通图可以有多个生成树

• 一个连通图的所有生成树都包含相同的顶点个数和边数（顶点：n，边：n - 1）

• 生成树当中不存在环（不能满足边数）

  判断环的行为也能引出很多算法，后续我将详细道来~

• 移出生成树中的任意一条边都会导致图的不连通（只能是n - 1，也是构成最小生成树的最少边）

• 在生成树中添加一条边会构成环，对于包含n个顶点的连通图，生成树包含n个顶点和n - 1条边

• 对于包含n个顶点的无向完全图，最多包含$n^{n-2}$​棵生成树

2.2 思想

贪心算法

熟悉吗？在$Huffman$树中，我们的思想也是贪心算法。你还记得它的概念吗？

贪心算法：模仿贪心的人做决策的样子，每次操作选择最优的做法，不考虑长远的影响。

2.3 基本操作

如图：

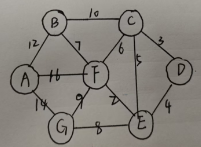
100条边中，选6条边，7个顶点，一直找权值的最小值。
加约束条件：不会形成环。（顶点之间）

• 先找权值最小的边——FE，这就将F和E两个顶点连接起来了。

• 之后，权值最小的边——CD，将C和D连接起来了。

• 接着，激活DE（4），这样的话CE（5），CF（6）不能再激活，因为会构成环

  这该如何判断成环呢？这也就就是判断几个顶点是否位于一个集合，这有没有很像并查集的操作呀~

• 然后，激活BF（7）和GE（8），$GF$​（9）会构成环，放弃激活，最后激活BA（12）。权值最小36。

2.4 代码

先前我们学习了多种存图的方法（邻接矩阵，邻接表，十字链表，邻接多重表，边集数组），到底该用什么方式实现$Kruskal$算法呢？

浅浅分析一下~
我们的核心目标是找边的最小值并且是有约束的（简单来说就是存边，对顶点要求不高），因此选择边集数组最合适。

注意：边集数组只是临时空间，顶点怎么存呢？其实，我们主要用来存图（通用图）的方式是邻接矩阵（刚好这里是无向图）。然后将其转成边集数组，再实现$Kruskal$​算法，来实现最小生成树。

2.4.1 定义结构

定义边集数组结构

// 定义边集数组的结构
typedef struct
{int begin;				// 边的起点（顶点1）int end;				// 边的终点（顶点2）int weight;				// 边的权值
} EdgeSet;

2.4.2 初始化边集数组

// 主要思路是利用邻接矩阵生成一个边集数组，利用边集数组实现Kruskal算法
// 刚好前面已经实现过邻接矩阵，可直接包含前面写的邻接矩阵的.h和.c文件
// 这里就不再写邻接矩阵的实现思路了// 从邻接矩阵中初始化边集数组，返回值表示边集数组的个数
void initEdgeSet(const MGraph *graph, EdgeSet *edges)
{int k = 0;// 遍历邻接矩阵的每一条for(int i = 0; i < graph->nodeNum; ++i)				// 遍历每个顶点{// 遍历邻接矩阵的上三角，避免重复，提升效率for(int j = i + 1; j < graph->nodeNum; ++j){if(graph->edges[i][j] > 0){edges[k].begin = i;edges[k].end = j;edges[k].weight = graph->edges[i][j];k++;}}}
}

2.4.3 排序边集数组

// 利用自排序——直接在原空间实现，不再产生新空间，进行拷贝
// 这里的思路是利用选择排序
void sortEdgeSet(EdgeSet *edges, int num)
{EdgeSet tmp;for(int i = 0; i < num; ++i){for(int j = i + 1; j < num; ++j){if(edge[j].weight < edge[i].wieght){memcpy(&tmp, &edge[i], sizeof(EdgeSet));memcpy(&edges[i], &edges[j], sizeof(EdgeSet));memcpy(&edges[j], &tmp, sizeof(EdgeSet));}}}
}

2.4.4 $Kruskal$算法 ★

• 定义并初始化一个并查集
• 对已排好序（从小到大）的边集进行操作：判断是否构成环（位于同一集合）
• 若不是，将该边放入到最小生成树中（知道边数到达n - 1）
• 释放并查集，返回权值

// Kruskal算法
// 基本思路：填边，返回权值之和
// 并查集实现
static int getRoot()
{while(uSet[a] != a){a = uSet[a];}return a;
}
int KruskalMGraph(const EdgeSet *edges, int num, int node_num, EdgeSet *result)
{// 定义一个并查集int *uSet;// 定义一个最小生成树的边的计数器int count;// 1. 初始化并查集uSet = malloxc(sizeof(int) * node_num);if(uSet == NULL){printf("malloc failed\n");return -1;}for(int i = 0; i < node_num; ++i){uSet[i] = i;}// 2. 从已经排序好的边集中，找到最小的边，不构成环for(int i = 0; i < num; ++i){int a = getRoot(uSet, edges[i].begin);int b = getRoot(uSet, edges[i].end);// 不构成环if(a != b){// 更新并查集uSet[a] = b;// 将边加到最小生成树中result[count].begin = edges[i].begin;result[count].end = edges[i].end;result[count].weight = edges[i].weight;// 累计权值sum += edges[i].weight;// 统计最小生成树边数count++;// 当边数满足：边数 = 总节点 - 1----->终止算法if(count == node_num - 1){break;}}}// 释放并查集free(uSet);// 返回权值之和return sum;
}

最终结果：

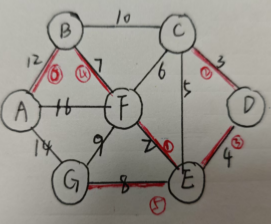
三、小结

本篇主要介绍了$Kruskal$​算法的基本实现，其基本思想是贪心，利用了邻接矩阵生成边集数组，利用选择排序对边按权值排序，并利用并查集判断是否构成环，最终生成最小生成树。

这里的选择排序可以利用更多先进的排序算法进行优化，当然，之后也会对排序算法进行一个系统的解读，期待$ing$。

下一篇将介绍另一种独特的找出最小生成树的算法——$Prim$算法。

希望各位多多赐教~