图的基本概述

图的基本概述

一、前言

今天，我们将开启一种新的结构的探索——图。它和我们日常生活中的图可以说是毫无关系。像先前表和树的初探一样，我将从逻辑结构和存储结构两个维度带你认识这个重要的结构。

二、逻辑结构

前情回顾：

表：元素和元素之间是$1：1$​的关系
树：元素和元素之间是$1：n$的关系

在图结构中，元素和元素之间是$m：n$​​的关系。

如图：

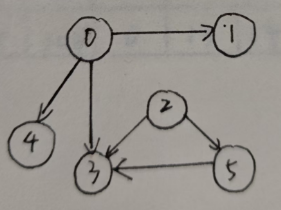
它可以是这样的~

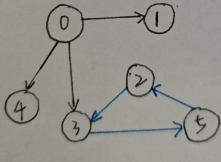
也可以是这样的~

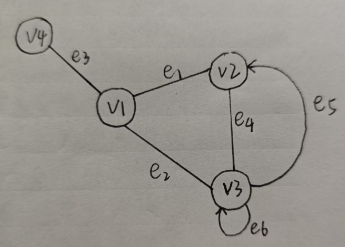
从图中可以很好地看出：图是由两个集合V和E组成，记为G = (V, E)，其中V是顶点的有限非空集合（$v1,v2,v3$），E是V中顶点偶对的边的集合（$<v1,v4>,<v2,v3>$）。

三、基本术语

图的基本术语比较多，先做了解，我尽量简洁概括~

意义：这些图结构的不同性质为之后的算法或工程的结构选择提供了选择。

3.1 简单图

不存在自己指自己的边，同一条边不重复出现，这样的图即为简单图。

非简单图就是复杂图啦~在这里基本不做深入研究

如图：

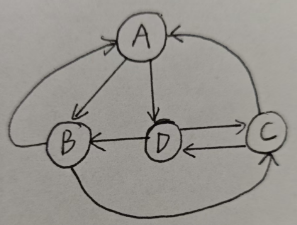
3.2 无向图 VS 有向图

3.2.1 无向图

代表边的顶点偶对是无序的，即$(Vi,Vj)=(Vj,Vi)$，是表示为同一条边的，即为无向图。无向图中的边一般表示为$(Vi,Vj)$。

如图：

3.2.2 有向图

和无向图相反，边的表示存在方向性。如$<Vi,Vj>$，这里$Vi$表示弧尾，$Vj$表示弧头。

如图：

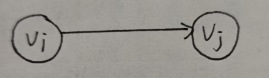
3.3 有向无环图

它的概念可谓见名知意，每一条边都有明确的方向。但是从任一顶点触发无法经过若干条边回到该顶点，就是有向无环图。

比如：快递如果不能送到你家，就只能打道回府，不能去往别处。（定向）

如图：

正版：

盗版（有环）：

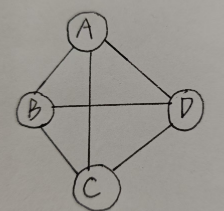
3.4 完全图

任何两个顶点之间都存在一条边，就是完全图。

3.5 子图

某个图的顶点集里一部分，边集里一部分，形成的图就是该图的子图（当然可以有一方[边/顶点]是完整的原图的集合）

3.6 端点、邻接点

在无向图中，存在一条边(i, j)，则称顶点i和顶点j为该边的两个端点，并称它们互为邻接点。

在有向图中，若存在一条边<i, j>，则称该顶点i和顶点j为该边的两个端点。它们互为邻接点。此时，顶点i为起点，顶点j为终点。

3.7 顶点的度、入度和出度

度、入度和出度在树结构中出现过。在这里它们会有怎样别样的表达呢？

注意：这里入度和出度的概念就只针对有向图了~

3.7.1 顶点的度

在无向图中，顶点所具有的边的数目（和树一样）。

3.7.2 入度和出度

仅针对于有向图。

• 入度（$In-degree$​）

  以该顶点出发的边的数量

• 出度（$Out-degree$​）

  以该顶点为终点的边的数量

3.8 路径和路径长度

这里的路径和$Huffman$树中提到的路径相似。

路径就是顶点之间经过的边。但是在图中会出现一个情况就是：顶点之间的路径往往不只一条，从而出现了最短路径的的经典算法。（这里我们后文详细讲~）

路径长度就是一条路径上经过的边的数目。

3.9 回路成环

一条路径上起点和终点为同一顶点，则称此路径为回路或者环。

有两种独特的环路（后续会详细讲）：

• 欧拉环路

  经过图中各边且恰好一次的环路，称之为欧拉环路，也就是其路径长度 = 图中边的总数。

• 哈密尔顿环路

  经过图中各顶点都恰好一次的环路，称作哈密尔顿环路，其路径长度 = 构成环路的边数。

3.10 连通、连通图和连通分量

3.10.1 连通

顶点x和顶点y之间存在可相互抵达的路径（直接或间接的路径），则称x和y是连通的。

3.10.2 连通图

图G中任意2个顶点都连通，则G为连通图，否则称为非连通图。

如图：

3.10.3 连通分量

无向图G中的极大连通子图称为G的连通分量。

对于连通图只有一个极大连通子图，就是它本身。（唯一的）而非连通图有多个极大连通子图，非连通图的极大连通子图就是连通分量。

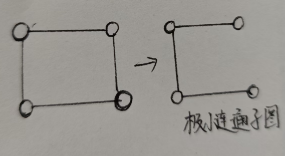
极大连通子图：参与构成连通图的最大顶点数量，形成的图。（再额外加顶点就不连通了）

极小连通子图：和后面的最小生成树有很大的关系。
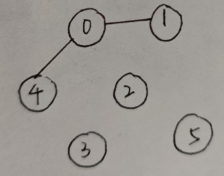
如图：

上图中极大连通子图就是其本身啦~

3.11 强连通图和强连通分量

3.11.1 强连通图

图G中任意两个顶点都连通（即存在路径），则图G就是强连通图。

3.11.2 强连通分量

强连通图只有一个强连通分量，即自身。非强连通图可能有多个强连通分量。

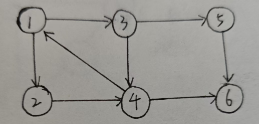
如图：

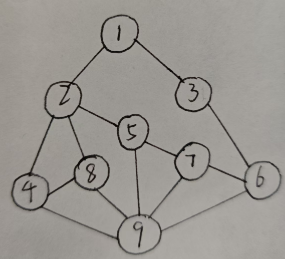
上图中：强连通分量有：{1, 2, 3, 4}、{5}、{6}

3.12 稠密图和稀疏图

通常认为边小于$nlogn$（n为顶点个数）的图是稀疏图，反之为稠密图。

3.13 权和网

3.132.1 权

图中每一条边都可以被赋予一个值，这个就是权。权表示一个顶点到另一个顶点的距离或者花费的代价。

注意：权可以是小数或负数，不是只有正数哦~

3.13.2 网

边上带有权的图称为带权图，也称之为网。

四、存储结构

前面我们知道了图就是两个集合：顶点集和边集。而存储结构将会告诉你顶点该怎么存，边该怎么存。

众所周知，存储结构可大致分2种：数组存储，链式存储。彼此搭配，就造成了图的不同存储方式。且听我细细道来~

4.1 邻接矩阵

4.1.1 顶点

采用数组，这种方式叫邻接（数组中元素之间都是紧挨着的）

存顶点，需要存它的值，可以用数组，为什么呢？
顶点的目的就是为了支撑它的边，如果用指针来存，指针需要指来指去，这就导致存储关系的存储会浪费很多空间（存地址），因此就不考虑链式存储了，直接采用数组来存。

4.1.2 边

采用数组——二维数组（矩阵）

这就造就了图的一种存储方式——邻接矩阵表示法。

4.2 邻接表

边可以采用链表的方式。

以A为顶点，可以到达其他几个点，就像是以A为钥匙，可以打开其他几扇门，这就类似指针。因此，可以利用链式存储，类似节点的存储方式。

顶点A可以分为数据域和指针域，数据域可以存它的值，指针域就存A顶点可以到达的顶点地址。

顶点还是数组（邻接），这就造就了图的另一种存储方式——邻接表。

4.3 抽象到具体

咱直接对上述方法上图阐释~

4.3.1 邻接矩阵

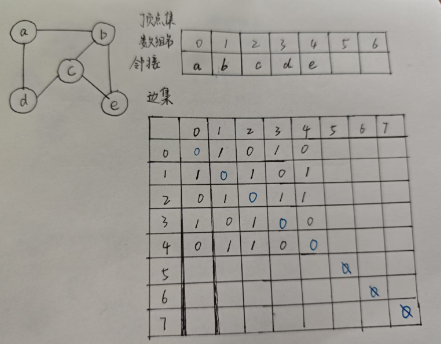
细节：对于数组存储的方式，下标扩容很难了，因此就预留一个足够大的空间，定义为MAX_NUM

注意：

• 这里是无向图，因而不存在自己指自己的情况，对应图中就是那个“对角线”——都是0。

• 最终结果可以看出，沿“对角线”，左右的元素是相同的（因为都是表示的一条边）

适用范围：无向图（更好）、有向图。

无向图：因为无向图的边是双向的（2倍的关系），从而形成了对称矩阵，就像上图所展示的。但是，对于有向图来说，边的指向是确定的，形成的矩阵就是稀疏的——有很多0（这完全取决于边的数量）。

优点：

• 通用性强，之后的很多算法都对它有所应用（后续都会展开讲的~）

• 找度或入度和出度很方便，

  如何找一个点的度，入度和出度？

  无向图找度：遍历一行/一列
  有向图找入度和出度：入度（列），出度（行）

缺点：

• 对于有向图，会造成空间的浪费。（边很少，但顶点很多时）

解决方法：邻接表

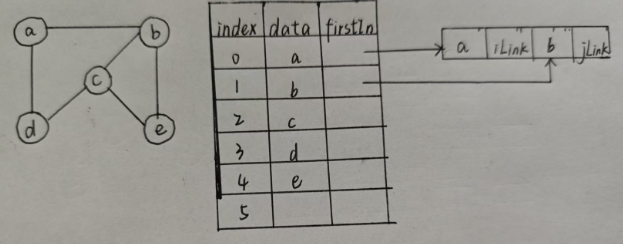
4.3.2 邻接表

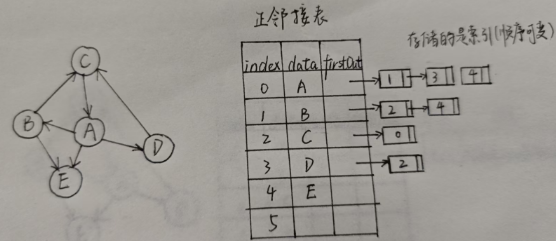
特点：用节点表示边（不会存无向图）

会有另外的表来存无向图——邻接多重表（见后文）

细节：

该如何存边呢？

• 用顶点索引作为出度的弧尾，节点用来存储弧头

• 后面不断指向下一个点（无序）

• 入度、出度：

  • 计算入度（多少点指向“我”）：遍历所有节点（$O(E)$​），效率比较低。
  • 计算节点的出度数——遍历

优点：节省空间

缺点：计算入度不方便

解决方法：逆邻接表（还是用来存有向图）

4.3.3 逆邻接表

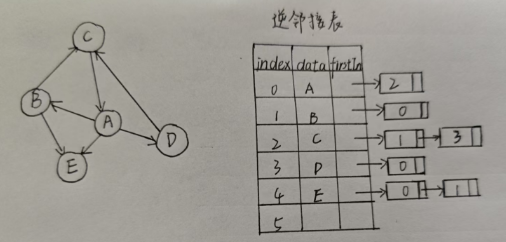
本质：就是正邻接表的指针域颠倒位置，就形成了逆邻接表

细节：用节点表示边，用顶点索引表示弧头，节点来存储弧尾

优点：计算入度方便

缺点：计算出度方便

如果又想搞入度，又想搞出度呢？

解决方法：十字链表

4.3.4 十字链表法

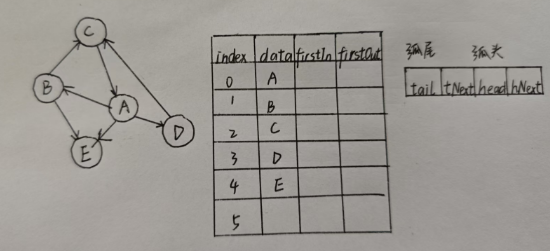
本质：正邻接表和逆邻接表的合体

细节：顶点结构：表示入度首地址和出度的首地址

优点：计算入度和出度想对更加方便。

缺点：不好表示无向图，表示起来很麻烦

解决方法：邻接多重表

4.3.5 邻接多重表

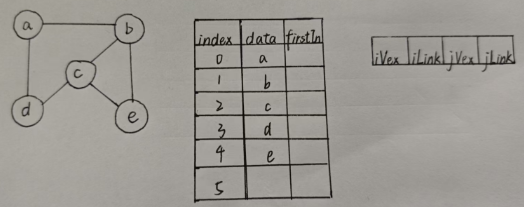
细节：无向图，有多少条边，用多少节点来表示

优点：节约空间

缺点：代码实现要复杂得多

在删除链表时，有两个顶点指向同一条边，删除时易造成其中一个指向变成野指针，因此两个都要找。

如图：

4.3.6 另一种存储：边集数组

边的存储不再依靠链表和矩阵

细节：边的存储直接存一个序列对：<1, 2> <1, 3>

应用：对顶点要求不高时会用边集数组

用的不多，在最小生成树中会用到（后续会讲~）

五、小结

开启了新的篇章~

希望大家多多指教~