【SOA仿真】SOA增益饱和特性仿真2
引言
为了更好的理解SOA的特性,见合八方近期将会发布【SOA仿真】系列文章。
SOA的仿真,通常离不开载流子速率方程、传输方程、以及增益方程这三大方程,在上一篇《SOA仿真】SOA增益饱和特性仿真1》中,我们根据增益方程分析了SOA的增益饱和特性,该仿真由实际测试的输出饱和光功率Psat_out和峰值波长的小信号增益G0仿真绘制了增益饱和特性曲线。本篇文章将进一步根据SOA本身的结构参数(如波导长度、波导体积)、特性参数(增益系数、透明载流子浓度,耦合参数),注入参数(偏置电流、输入光功率)等作为输入,结合简化的载流子速率方程,仿真求解SOA的增益特性。
关键词
半导体光放大器SOA、增益、小信号增益、增益饱和、仿真、载流子、速率方程
1.增益公式
半导体光放大器的增益介质由材料增益系数g(单位:每单位长度)来表征,该系数与载流子密度N相关,如下面公式[3]:
![]()
其中N0为透明载流子密度,a为微分增益参数。对于SOA的小信号净增益系数g0(又称为未饱和增益系数)则由下面公式给出
![]()
其中Γ是限制因子,a是材料增益,αs是波导内部散射损耗。进一步的,由g0可以得到SOA中的小信号增益(或称未饱和增益),由下面公式给出

其中L是波导长度。
2.速率方程
当光和电流注入半导体光放大器(SOA)时,其有源区内的载流子密度N会发生变化。这些变化可通过载流子速率方程进行描述[3]:
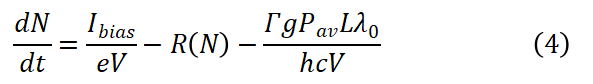
该简化的速率方程描述了载流子的主要“产生”和“消耗”来源,右侧第一项是电流注入带来的载流子变化,其中Ibias是SOA的偏置电流,e是电子电荷,V是有源波导体积(V=L*W*H, L,W,H分别代表有源波导的长度、宽度和厚度)。
速率方程中右侧的第二项R(N)是载流子复合速率,它也与N相关:
![]()
式中右侧的三项分别是表面缺陷复合、辐射复合和俄歇复合,相应的,其中A为表面缺陷复合系数,B为辐射复合系数,C为俄歇复合系数。
速率方程公的第三项为受激辐射,其中Pav是平均光功率。
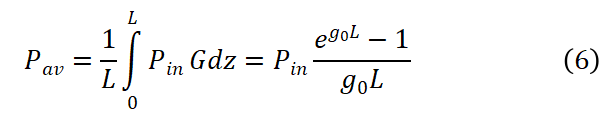
在稳态时,载流子达到平衡,此时dN/dt=0,我们得到:
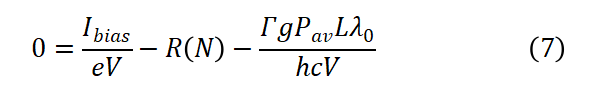
3.仿真
可以看出,公式7可采用二分迭代法求解,具体如下:
第一步:设置参数
设置载流子速率方程和增益方程所需参数,本文选用了文献[3]的参数。
各参数含义与物理意义:
参数 | 物理意义 | 取值 | |
输入参数 | Ibias | 注入电流 | 0mA-300mA |
Pin | 输入光功率 | -30dBm | |
物理常数 | e | 电子电荷 | 1.6*1019C |
c | 真空中光速 | 3*1010m/s | |
h | 普朗克常数 | 6.62606896*10-34 | |
SOA特性参数 | L | SOA有源区长度 | 500um |
W | SOA有源区宽度 | 3um | |
H | SOA有源区高度 | 0.08um | |
Γ | 限制因子 | 0.3 | |
N0 | 透明载流子浓度 | 1.4*1024/m3 | |
Ni | 初始载流子浓度 | 3*1024/m3 | |
A | 表面缺陷复合系数 | 1.43*108/s | |
B | 辐射复合系数 | 1*10-16m3/s | |
C | 俄歇复合系数 | 3*10-41m6/s | |
a | 微分增益 | 2.78*10-20m2 | |
α | 波导散射损耗 | 40*102/m | |
λ0 | 增益谱峰值波长 | 1550nm |
第二步:迭代求解增益方程


图2 SOA分段求解示意图
首先我们将波导切割为n段,本文中切割了10段(k=0,1,…9),逐段依次计算,我们设每端的输入和输出光功率分别为Pin[k],Pout[k],计算步骤如下:
- 设置初始值:注入电流I_bias取值0~300mA,外部输入光功率-30dBm做为第一段的输入光功率,从第一段开始计算k=0,并设置Pin[0]=-30dBm;
- 使用二分迭代方法(详见附录),计算该段的载流子浓度N[k];
- 通过公式1,2,3,计算G[k];
- 通过获得的G[k],得到该段的输出光功率Pout[k]=Pin[k]*G[k],并将该值做为下一段的输入光功率Pin[k+1]=Pout[k],重复上面步骤,直到段尾。
第三步:绘制仿真增益曲线
将上面计算结果转为我们习惯的对数坐标后,绘制曲线如下:
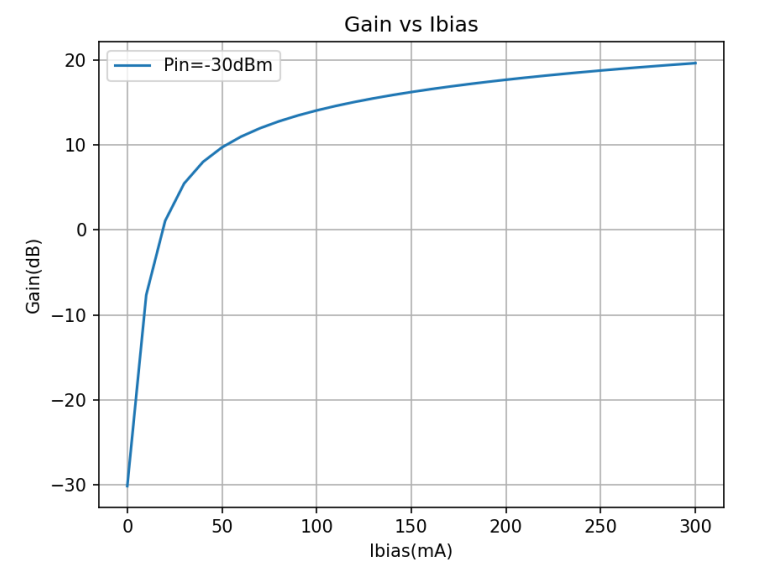
图3 SOA仿真的电流和增益曲线
4.结论和后续
本文利用简化的载流子速率方程,以及二分法迭代,仿真得到了外部注入(电流及输入光功率)与增益的关系。
后续我们还将仿真增益与波长的关系(增益谱曲线),以及增益的动态特性。
附录 二分法
二分法(Bisection Method) 是一种简易的数值计算方法,用于在连续函数的闭区间内寻找方程的根(即函数值为0的点)。其核心思想是通过不断将区间二等分,缩小根所在的范围,直至达到所需的精度。
基本原理
二分法的应用需满足前提条件:函数f(x)在闭区间[a, b]上连续;并满足f(a)*f(b)< 0(根据介值定理,此时区间内必存在至少一个根)。
步骤如下:
- 计算区间中点c =(a+b)/2;
- 计算中点的函数值f(c):
- 若f(c) = 0,则c即为方程的精确解,结束计算;
- 若(f(a)*f(c)<0,说明根在区间[a,c]内,令新区间为[a, c];
- 若f(c)*f(b)<0,说明根在区间[c, b]内,令新区间为[c, b];
- 重复步骤 1 和 2,直至区间长度|b-a|达到期望精度(如10^-6)),此时区间中点可作为根的近似值。
参考文献
[1] Niloy K. Dutta and Qiang Wang, “Semiconductor Optical Amplifiers,” 2nd edition, World Scientific Publishing Company, 2013.
[2] 王光全,沈世奎,王伟,曾志超等,“半导体光放大器SOA技术与应用白皮书”,2024版
[3] Aziz, Ahmed & Ng, Wai & Aly, Moustafa & Chiang, Ming. (2008). “Optimisation of the key SOA parameters for amplification and switching”.
