时间序列早期分类中的置信度累积问题:从ECE-C到时序依赖建模
完整代码+数据下载地址:Early-classification-algorithm-for-time-series资源-CSDN下载
# 时间序列早期分类中的置信度累积问题:从ECE-C到时序依赖建模
## 引言
在时间序列早期分类领域,置信度累积是一个既关键又棘手的问题。今天我们来深入探讨一下ECE-C算法中的置信度累积机制,以及为什么简单的独立假设在实际应用中会遇到困难。
## ECE-C算法的置信度累积机制
ECE-C(Early Classification with Confidence)算法采用了一种看似直观的置信度累积策略:
置信度 = (1-p1) × (1-p2) × ... × (1-pn)
其中,pi表示第i个时间步预测为错误类别的概率。
### 算法逻辑分析
这种累积方式基于以下假设:
- 独立性假设:各时间步的预测相互独立
- 乘法累积:通过连乘方式累积置信度
- 错误概率转换:将正确概率转换为错误概率进行累积
## 独立假设的问题
### 理论缺陷
时间序列数据天然具有时序相关性,独立同分布假设在理论上是不合理的:
1. 物理连续性:温度、压力等物理量连续变化,相邻时间步必然相关
2. 信息传递:早期预测结果会影响后期预测的准确性
3. 状态依赖:系统状态在时间维度上具有马尔可夫性质
### 实际影响
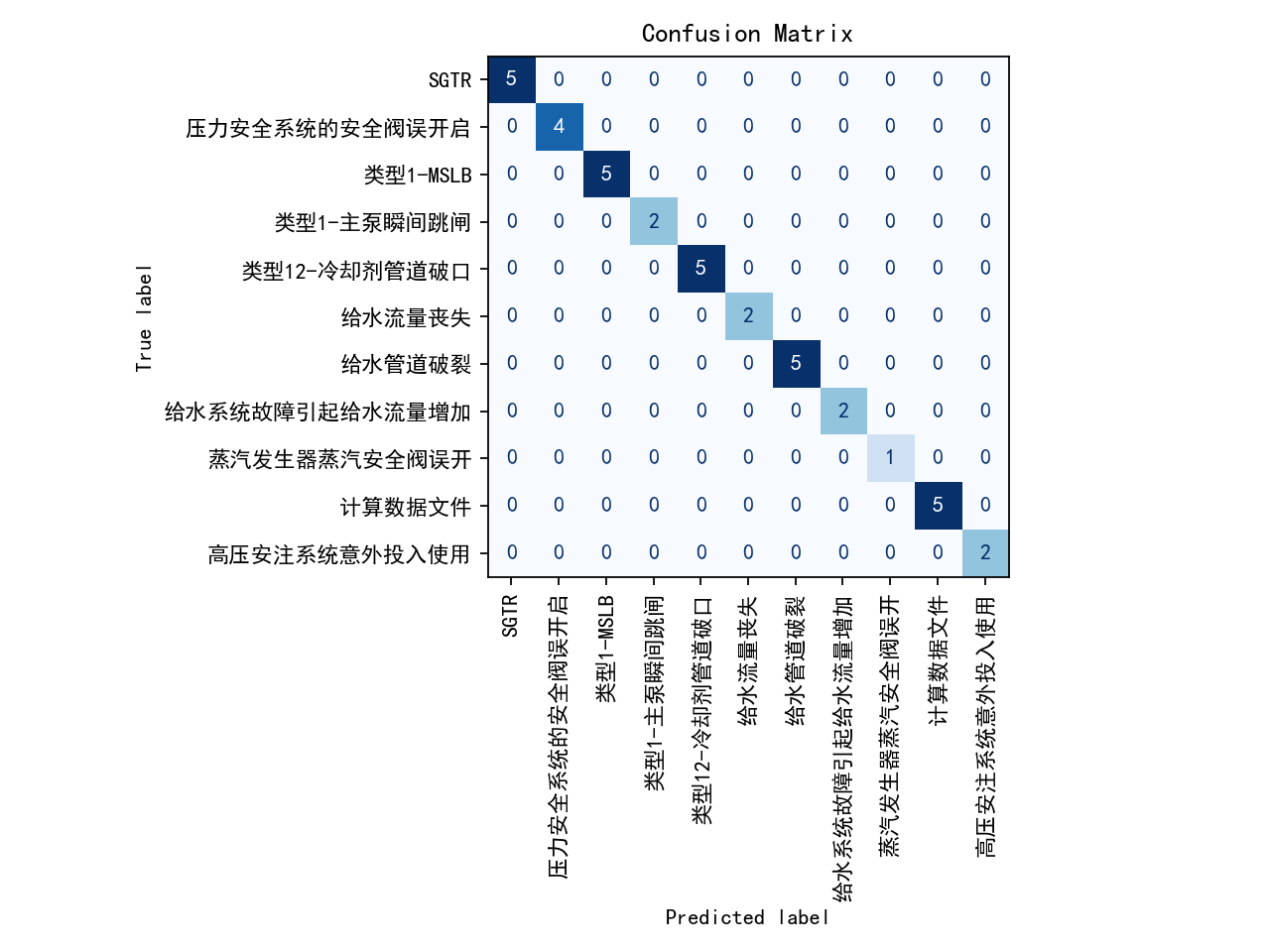
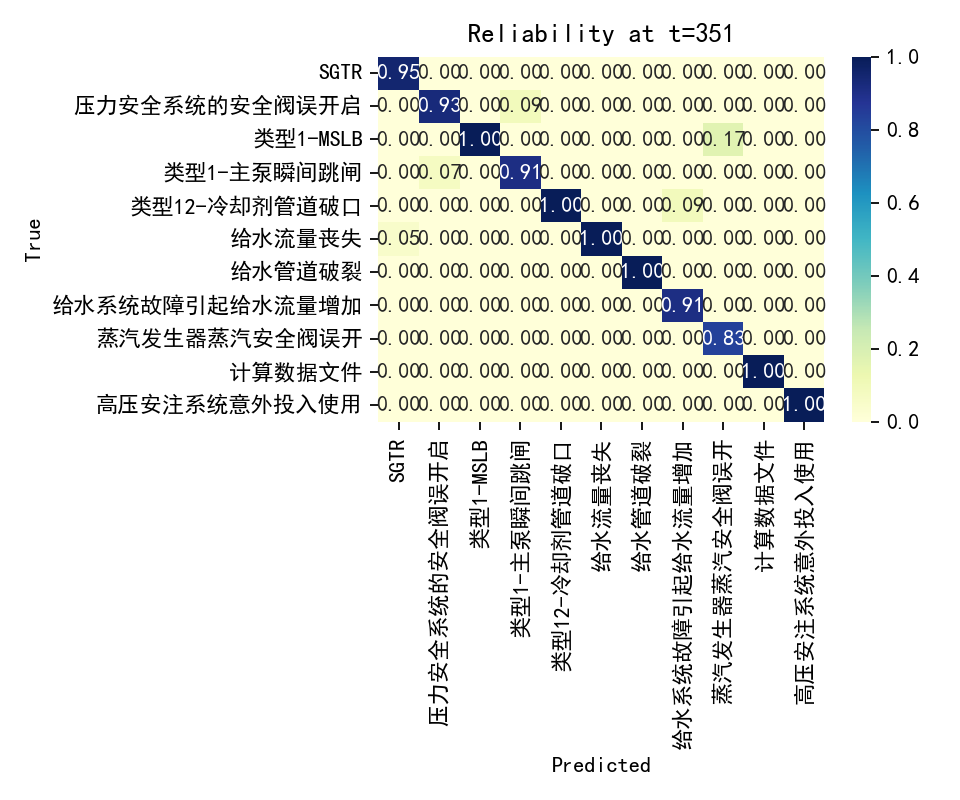
错误的独立假设会忽略时序依赖关系,导致置信度计算不准确。比如在核电站事故预测中,前几秒的压力变化会直接影响后续的温度预测,但独立假设完全忽略了这种关联。
## 核心难点分析
### 1. 数学形式未知
最难解决的问题:时序依赖的数学形式未知。我们无法确定:
- 早期预测如何影响后期预测
- 依赖关系的具体数学表达
- 权重如何随时间衰减
### 2. 数据稀缺性
早期分类场景下,标注数据极其稀缺:
- 需要大量带时间戳的标注数据
- 不同时间步的标注成本高
- 难以获得完整的时序标注
### 3. 计算复杂度
考虑时序依赖会带来:
- 指数级增长的计算复杂度
- 实时性要求与精度的平衡
- 参数调优的困难
## 可能的改进方向
### 1. 条件概率建模
使用条件概率而非独立概率:
P(类别|t1,t2,...,tn) ≠ P(类别|t1) × P(类别|t2) × ... × P(类别|tn)
### 2. 指数加权移动平均
引入时间衰减权重,让近期预测对置信度影响更大:
置信度 = ∏(1-pi)^(α^(n-i))
### 3. 预测一致性检验
只有连续几个时间步预测一致时才累积置信度,避免噪声影响。
### 4. 动态权重调整
根据预测的历史准确性动态调整权重,让更可靠的预测步骤获得更高权重。
## 总结
时间序列早期分类中的置信度累积问题看似简单,实则涉及深层的时序依赖建模挑战。ECE-C算法的独立假设虽然简化了计算,但在理论上存在缺陷。真正的解决方案需要:
1. 理论突破:建立合理的时序依赖数学模型
2. 数据驱动:利用大量标注数据学习依赖关系
3. 工程优化:在计算复杂度和精度间找到平衡
这个问题目前仍然是该领域的一个开放性问题,需要更多的理论研究和工程实践来推动解决。
欢迎在评论区分享您对时序依赖建模的看法和经验!
---
这就是一篇完整的CSDN博客内容,去掉了Markdown格式标记,直接可以复制粘贴使用。
