The 2025 ICPC Asia East Continent Online Contest (I) - H.Walk（网格图对偶建模、最小割建模）

原题链接：Walk

题目大意

在二维平面上，你初始位于点 $(0,0)$，目标是前往点 $(N,M)$。若你当前处于位置 $(x,y)$，下一步可移动到 $(x+1,y)$ 或 $(x,y+1)$。你走过的路径定义为：依次连接每一步位置所形成的、从 $(0,0)$ 到 $(N,M)$ 的折线。

存在 $K$ 个矩形。第 $i$ 个矩形的左下角坐标为 $(x_{i,1}-0.5,y_{i,1}-0.5)$，右上角坐标为 $(x_{i,2}+0.5,y_{i,2}+0.5)$。若你走的路径同时与该矩形的左边界和右边界相交，需承担 $a_i$ 的成本；若路径同时与该矩形的上边界和下边界相交，需承担 $b_i$ 的成本。总费用定义为所有矩形产生的成本之和。

你需要求出从 $(0,0)$ 到 $(N,M)$ 所需的 最小总费用。

样例输入：

1 2 1
0 1 1 1 1 2

样例输出：

2

题目分析

• 经典的网格图转对偶图处理，对于每一个方格/横边/竖边，从左到右，从上到下标号，对于一张 $n\times m$ 的网格图，网格图中的标号 $idx$ 的边与对偶图中 $(u,v)$ 有如下关系，其中 up 和 down 用于找横边，left 和 right 用于找竖边：

// S 为源点, T 为汇点
int up(int idx) {return idx <= m ? S : idx - m;}
int down(int idx) {return idx > n * m ? T : idx;}
int left(int idx) {return (idx % (m + 1)) == 1 ? T : idx - (idx - 1) / (m + 1) - 1;}
int right(int idx) {return (idx % (m + 1)) == 0 ? S : idx - idx / (m + 1);}

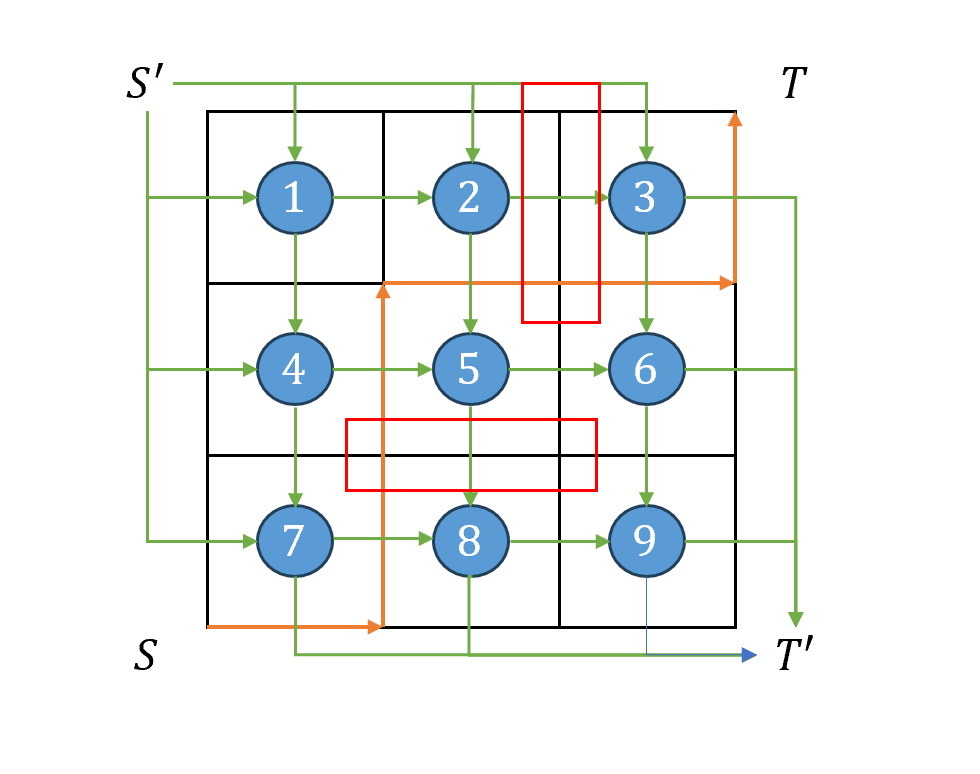
• 此时网格图上的一条合法路径对应对偶图上的一个割，现分析同时穿过矩形左右/上下两边在对偶图上的表现形式。图中绿色有向线为网络流流向，红色线框为矩形，橙色有向线为一条从 $(0,0)$ 到 $(N,M)$ 的合法路径。任意一条合法路径（即一个割）都如图所示，将左上半部分划分到 $S^{\prime }$ 中，将下半划分到 $T^{\prime }$ 中。考虑最下方的矩形，也就是路线穿过矩形上下两边的情况，容易发现该路线将节点 $4,7$ 划分到了 $S^{\prime }$ 中，将节点 $6,9$ 划分到了 $T^{\prime }$ 集合当中，若改变路径但使得其同样穿过矩形上下两边，那么恒有节点 $4,7$ 被划分到 $S^{\prime }$ 中，节点 $6,9$ 被划分到 $T^{\prime }$ 中。
• 分析发现，若节点 $7$ 被划分到了 $S^{\prime }$ 且节点 $6$ 被划分到了 $T^{\prime }$，那么必有 $7$ 号节点及其左上半所有部分都被划分到了 $S^{\prime }$，$6$ 号节点及其右下部分都被划分到了 $T^{\prime }$ 中，由于 $4$ 号节点为矩形左上角对应节点，故其相对于矩阵左下角节点而言，必在其左上方，对于 $9$ 号节点同理分析，所以 $7$ 号节点被划分到 $S^{\prime }$ 且 $6$ 号节点被划分到 $T^{\prime }$ 为路线穿过矩形上下两边的充要条件。故有，当矩形左下角对应节点被划分到 $S^{\prime }$ 且矩形右上角对应节点被划分到 $T^{\prime }$ 时路线穿过矩形上下两边；同理分析有，当矩形左下角对应节点被划分到 $T^{\prime }$ 且矩形右上角对应节点被划分到 $S^{\prime }$ 时路线穿过矩形左右两边。
• 故问题变为关于两点关系最小化组合代价问题，当且仅当两点被划分到不同集合时才会有对应代价，取左下角对应节点为 $x$，右上角对应节点为 $y$，根据该问题一般建模模型可知，连边 $x\to y$，容量为 $b$；连边 $y\to x$，容量为 $a$。当 $x,y$ 被划分到同一集合时，这两条边边不会产生任何作用，当且仅当 $x,y$ 被划分到不同集合中时，最小割才会加进去对应的组合代价，
• 由于网格图中的一个合法路径一定是最短路，而对偶图中的最小割对应一条网格图当中的最短路，但原问题中的路径没有权值，为了确保路径是最短路，给对偶图中每一个边容量设置为一个足够大的整数 $W$，保证了其一定沿最短路行动，最小割即为 $(n+m)\cdot W$。在加入组合代价对应的连边之后，求得最小割后再将其数值减去 $(n+m)\cdot W$ 即可。

代码答案

#include<bits/stdc++.h>
#define endl '\n'using namespace std;
using ll = long long;const ll INF = 5e7;
const ll LLINF = 0x3f3f3f3f3f3f3f3fll;const int N = 1e4 + 10, M = 2e6 + 10;
int n, m, k, S, T, tot = 1;
int head[N], cur[N], d[N];struct edge {ll v, nxt, c;
} edges[M];void add(int u, int v, ll c) {edges[++tot] = {v, head[u], c}, head[u] = tot;edges[++tot] = {u, head[v], 0}, head[v] = tot;
}bool bfs() {memset(d, 0, sizeof(d));queue<int> q;q.push(S); d[S] = 1;while(q.size()) {int u = q.front(); q.pop();for(int i = head[u]; i; i = edges[i].nxt) {int v = edges[i].v;if(!d[v] && edges[i].c) {d[v] = d[u] + 1;q.push(v);if(v == T) return true;}}}return false;
}ll dfs(int u, ll mf) {if(u == T) return mf;ll sum = 0;for(int i = cur[u]; i; i = edges[i].nxt) {cur[u] = i; // 当前弧优化int v = edges[i].v;if(d[v] == d[u] + 1 && edges[i].c) {ll res = dfs(v, min(edges[i].c, mf - sum));edges[i].c -= res;edges[i ^ 1].c += res;sum += res;if(sum == mf) break;}}if(!sum) d[u] = 0;return sum;
}ll dinic() {ll flow = 0;while(bfs()) {memcpy(cur, head, sizeof(head));flow += dfs(S, INF);}return flow;
}int up(int idx) {return idx <= m ? S : idx - m;}
int down(int idx) {return idx > n * m ? T : idx;}
int left(int idx) {return (idx % (m + 1)) == 1 ? S : idx - (idx - 1) / (m + 1) - 1;}
int right(int idx) {return (idx % (m + 1)) == 0 ? T : idx - idx / (m + 1);}int main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);cin >> n >> m >> k;swap(n, m);S = 0, T = n * m + 1;for(int i = 1; i <= n + 1; i++) {for(int j = 1; j <= m; j++) {int id = (i - 1) * m + j;add(up(id), down(id), INF);}}for(int i = 1; i <= n; i++) {for(int j = 1; j <= m + 1; j++) {int id = (i - 1) * (m + 1) + j;add(left(id), right(id), INF);}}for(int i = 1; i <= k; i++) {int x1, y1, x2, y2, a, b; cin >> x1 >> y1 >> x2 >> y2 >> a >> b;if((x1 == 0 && y1 == 0) || (x2 == m && y2 == n)) continue;int ld = (n - y1) * m + x1, ru = (n - y2 - 1) * m + x2 + 1;if(x1 == 0) ld = S;else if(y1 == 0) ld = T;if(x2 == m) ru = T;else if(y2 == n) ru = S;add(ld, ru, b), add(ru, ld, a);}cout << dinic() - INF * (n + m) << endl;return 0;
}