第三次周赛题解
A lwy购物
这个其实是完全背包,但因为数据改了改,可以暴力写出
#include<bits/stdc++.h>
using namespace std;
int dp[10050];
int b[7];
int a[7]={0,1,5,10,20,50,100};
int main(){int n;cin>>n;memset(dp,0x7f,sizeof(dp));for(int i=1;i<=6;i++){cin>>b[i];}dp[0]=0;for(int i=1;i<=6;i++){for(int k=1;k<=b[i];k++){for(int j=n;j>=a[i];j--){dp[j]=min(dp[j],dp[j-a[i]]+1); }}}if(dp[n]==0x7f){cout<<-1;} else{cout<<dp[n];}}这个是暴力写法,注释都在上面
#include <bits/stdc++.h>
using namespace std;int amount; // 需要找零的金额
int ans = 0; // 记录所需硬币总数// 辅助函数:使用指定面额的硬币进行找零
// 参数a:当前面额硬币的可用数量
// 参数b:当前硬币的面额值
void fun(int a, int b) {// 如果剩余找零金额大于等于当前硬币面额if (amount >= b) {// 计算理论上最多需要多少个当前面额的硬币int t = amount / b;// 如果需要的硬币数量不超过库存if (t <= a) {ans += t; // 使用t个当前面额硬币amount = amount % b; // 更新剩余找零金额}else {// 如果库存不足,则使用全部可用的当前面额硬币ans += a; // 使用所有可用的当前面额硬币amount = amount - a * b; // 更新剩余找零金额}}
}int main() {// 读取需要找零的金额cin >> amount;// 定义数组存储各种面额硬币的库存数量int a[6];// 读取6种面额硬币的库存数量for (int i = 0; i < 6; i++) cin >> a[i];// 定义硬币面额数组,对应1元、5元、10元、20元、50元、100元int b[6] = {1, 5, 10, 20, 50, 100};// 从大到小遍历硬币面额(贪心策略:优先使用大面额硬币)for (int i = 5; i >= 0; i--) {fun(a[i], b[i]); // 处理当前面额的硬币}// 检查是否完成找零if (amount > 0)cout << -1; // 如果还有剩余金额无法找零,输出-1else cout << ans; // 输出所需硬币总数return 0;
}B day1-持石王松灯
#include<stdio.h>
#include<math.h>
#include<algorithm>
#include<stdbool.h> //使用布尔变量,c++代码不用
//提示中给出的是数学方法,四平方和定理
bool k_1(int x) { //判断x本身是不是完全平方数int y = sqrt(x);return y * y == x;
}
bool k_4(int x) { //对提示中公式的处理while (x % 4 == 0) {x /= 4;}return x % 8 == 7;
}
int solve(int n) {if (k_1(n)) {return 1;}if (k_4(n)) {return 4;}for (int i = 1; i * i <= n; ++i) {//勾股定理int j = n - i * i;if (k_1(j)) {return 2;}}//k值只有四种情况,其余的均为3return 3;
}//基础的动态规划解法
int solve1(int n) {// dp[i] 表示表示整数i所需的最少完全平方数个数int dp[n+1];// 从1开始计算到nfor (int i = 1; i <= n; ++i) {// 最坏情况:i全部由1组成,需要i个完全平方数int cnt = i;// 遍历所有可能的完全平方数 j*j <= ifor (int j = 1; j * j <= i; ++j) {// 状态转移方程:// 如果使用j*j这个完全平方数,那么剩余的部分是i-j*j// dp[i] = min(dp[i], dp[i - j*j] + 1)cnt = std::min(cnt, dp[i - j * j]);}// 加上当前使用的这个完全平方数dp[i] = cnt + 1;}return dp[n];
}int main() {int n;scanf("%d", &n);int sum = 0;for (int i = 1; i <= n; ++i) {int m;scanf("%d", &m);int j = i % 3;bool a = (j == solve(m)); bool b = (j == solve(m - 1)); bool c = (j == solve(m + 1));if (a || b || c) sum++;}printf("%d", sum);if (sum < (n + 1) / 2) {printf("\n咕咕嘎嘎~");}return 0;
}C wdh的博弈(hard)
这其实是一个nim博弈的模板题
给了n堆石子,每一堆都有数量,然后两个人轮流可以一次拿无数个石子(对于一堆石子来说),然后谁最后拿完所有石子谁赢
先说结论,对所有石子堆异或,求出来的和如果不等于0则先手赢,反之后手赢
看每个石子堆的石子数量的二进制
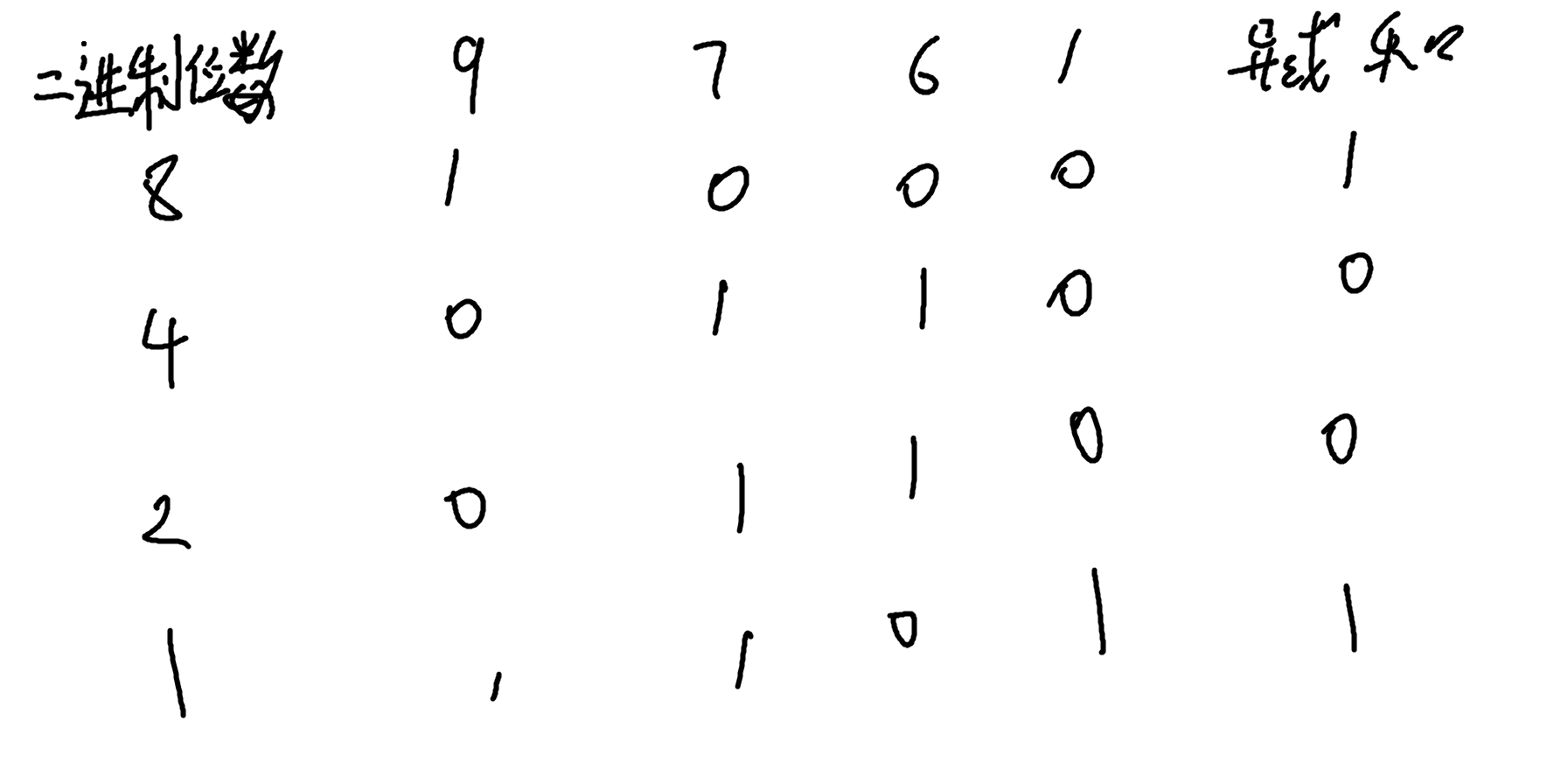
看着两个例子,我们只需看每一位二进制的异或和,然后我们再看最高位的异或和1,找到对应的数,看第1个图,最高位对应的数在9里面,我们就可以对9操作然后使得整个异或和为0,我们对这个石子堆拿走9个石子堆这样整个异或和就为0了
再看第二个图,异或和1最高位对应的在7里面,我们就只需要在这个石子堆里面拿走6,这样整个异或和就为0了,
所以我想说的是当所有石子堆异或和不为0时候我们可以对其进行任意操作可以将其变为0,然后还有一个重点就是当石子全部被拿走我们的石子堆的异或和也是0,所以我们在进行数次操作后,一定会转移到全部石子堆数量为0的情况,然后当一个人拿到的状态是所有石子堆异或和为0时候,对其进行拿走任意石子,一定会变成石子堆异或和不为0的情况,
所以当先手接到初始时候石子堆异或和不为0的情况,先手就可以对其操作让其变为0,然后给后手,这样进行数次操作,后手永远接收到的情况是异或和为0,那么总会到达所有石子堆都为0的情况
综上所述,当石子堆的初始异或和不为0,先手必胜,反之后后手必胜
#include<bits/stdc++.h>
using namespace std;
int t,n,s;
int main(){cin>>t;while(t--){s=0;cin>>n;for(int i=0;i<n;i++){int k;cin>>k;s^=k;} if(s==0){cout<<"No"<<endl;}else{cout<<"Yes"<<endl;}}
}D day2-zyf学姐和wdh学姐辩耄
思路:判断A,B,C三点的曲率是否相等,相等就输出喵~喵~喵。
//这题出的确实有点持石了,题面太长了,难度中等偏下吧,看大家都没写,orzzzzzzzz
#include<iostream>
#include<cmath>
#include<vector>
#include<algorithm>
using namespace std;
const double dev = 1e-9;
double solve(double x, int a, int b, int c, int d) {// 求一次导double y1 = 3 * a * x * x + 2 * b * x + c;//求二次导double y2 = 6 * a * x + 2 * b;double t = 1 + y1 * y1;t = t * t * t;return abs(y2) / sqrt(t);
}
bool fun(double a, double b) {return abs(a - b) <= dev;
}
int main() {vector<double> k;for (int i = 0; i < 3; ++i) {double x, y;char c1, c2, c3;cin >> c1 >> x >> c2 >> y >> c3;int a, b, c, d;cin >> a >> b >> c >> d;k.emplace_back(solve(x, a, b, c, d));}if (fun(k[0], k[1]) && fun(k[0], k[2])) {cout << "哈~哈~哈;";}else {cout << "喵~喵~喵。";}return 0;
}E wdh的博弈(easy)
这个是巴什博奕
因为如果一个人每次遇到的要拿的情况都是剩下m+1的倍数个物品,当最后一次遇到m+1那他也最多只能拿m个,最少拿1个,而下一个人就必定能一次性拿完,而且我们可以保证每个人是绝对聪明的,如果一个人有这个机会,他是可以使另一个永远面对拿m+1倍数个物品,所以我们就可以得到这个结论如果n能整除m+1那么后手的人赢 , 如果不能整除则先手赢
#include<bits/stdc++.h>
using namespace std;
int main(){int n,m;cin>>n>>m;if(n%(m+1)==0){cout<<"No";}else{cout<<"Yes";}return 0;
}F wx的画
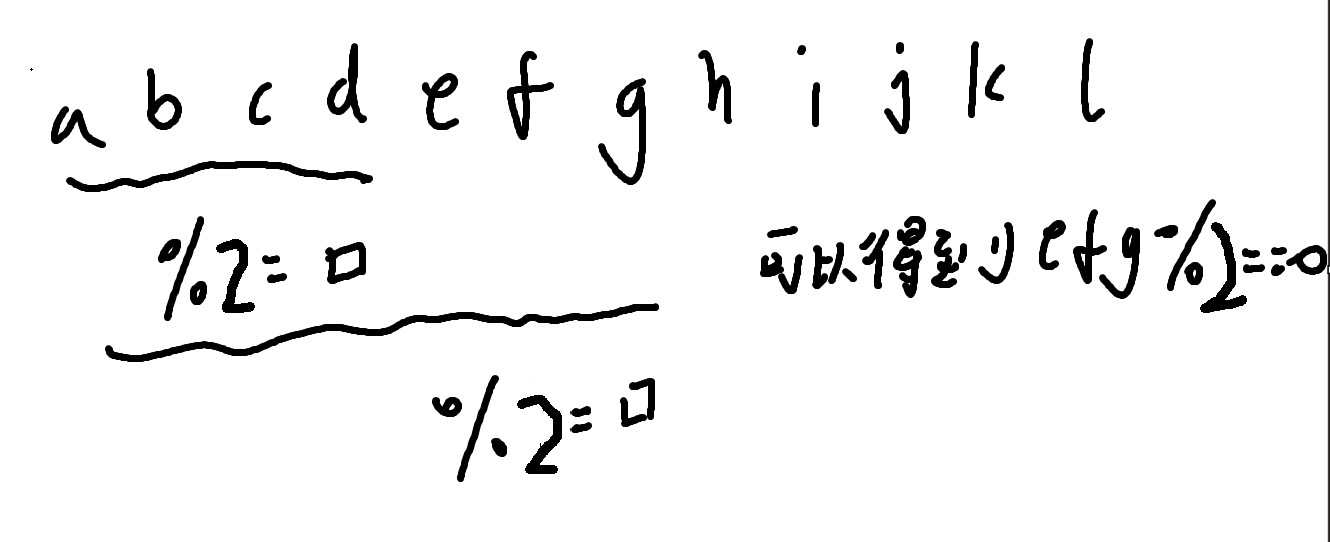
那我们可以用一个大小为2的数组就可以去存一下每一段模2之后的值,然后看之后好不好出现重复,出现了那我们就可以得到像上图一样的长度
#include<bits/stdc++.h>
using namespace std;
int arr[50020];
int n,mod2[2];
long long prefix;
int main(){ios::sync_with_stdio(false);cin.tie(nullptr);cin>>n;int max_len=0;memset(mod2,-1,sizeof(mod2));mod2[0]=0;for(int i=1;i<=n;i++){cin>>arr[i];(prefix+=arr[i])%=2;if(mod2[prefix]==-1){mod2[prefix]=i;}else{max_len=max(i-mod2[prefix],max_len);}}cout<<max_len;}G 简单的数学题
根据题意模拟即可
#include <bits/stdc++.h>
using namespace std;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);long long x1, y1, x2, y2, x3, y3;cin >> x1 >> y1 >> x2 >> y2 >> x3 >> y3;pair<long long, long long> d1, d2;d1 = make_pair((x2 - x1), (y2 - y1));d2 = make_pair((x3 - x2), (y3 - y2));if (d1.first * d2.second - d2.first * d1.second > 0) {cout << "left";}else if (d1.first * d2.second - d2.first * d1.second < 0) {cout << "right";}else {cout << "error";}return 0;
}H ~~简单的~~数学题
顺时针给出的点,每3个点连成2个向量,如果朝向相同则为凸多边形,否则为凹多边形。
#include<bits/stdc++.h>
using namespace std;pair<long long, long long> operator-(const pair<long long, long long> &p1, const pair<long long, long long> &p2) {return make_pair(p1.first - p2.first, p1.second - p2.second);
}long long cross(const pair<long long, long long> &p1, const pair<long long, long long> &p2) {return p1.first * p2.second - p1.second * p2.first;
}int main() {int n;cin >> n;vector<pair<long long, long long>> v(n);for (int i = 0; i < n; i++) {cin >> v[i].first >> v[i].second;}int sign = 0;bool f = true;for (int i = 0; i < n; i++) {int j = (i + 1) % n;int k = (i + 2) % n;long long c = cross(v[j] - v[i], v[k] - v[j]);if (c != 0) {if (sign == 0) {sign = (c > 0) ? 1 : -1;}else if ((c > 0 && sign < 0) || (c < 0 && sign > 0)) {f = false;break;}}}cout << (f ? 1 : -1);return 0;
}I 逃离二维宇宙(一)
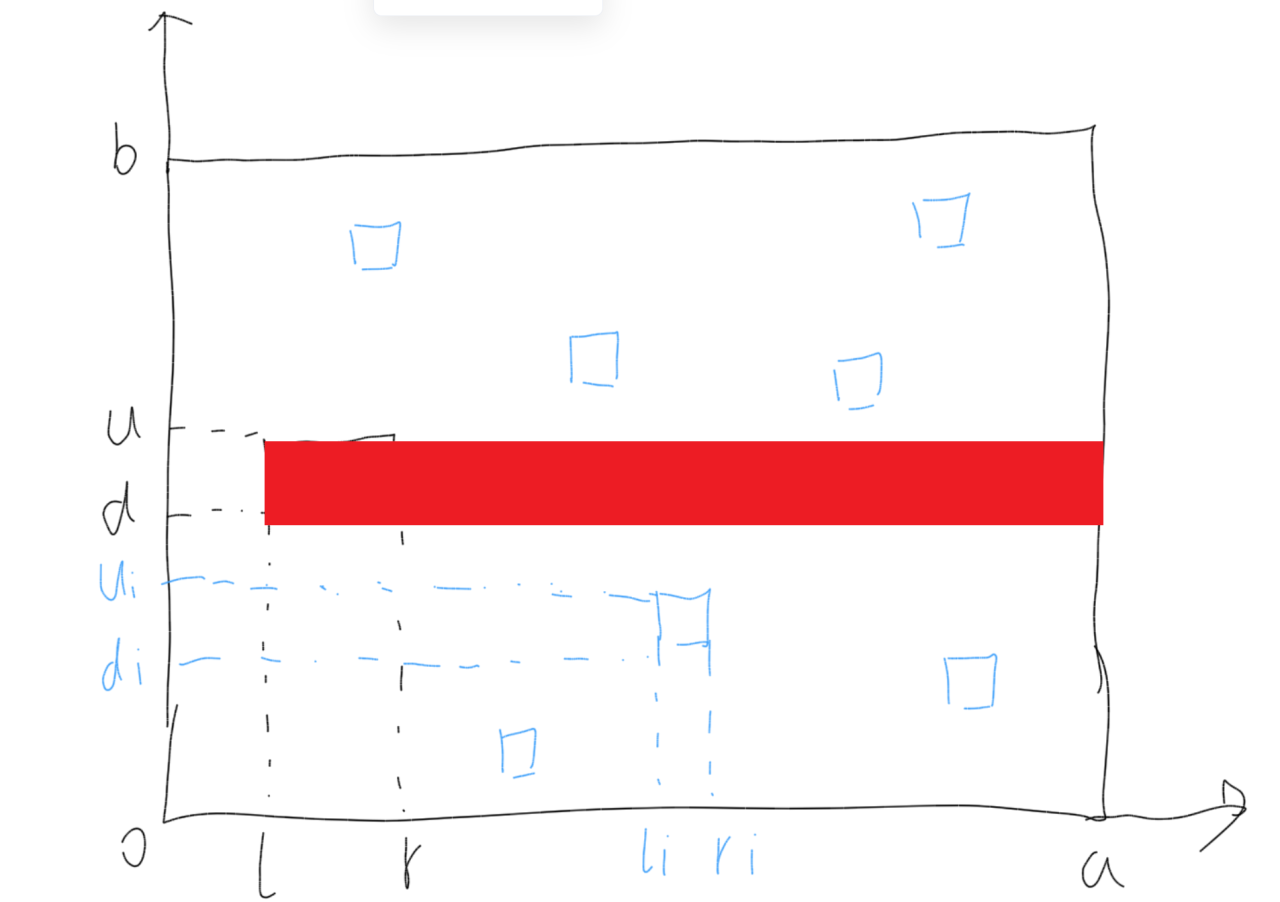
因为飞船只能向一个方向行驶,所以飞船的运动轨迹是一个如图的红色矩形,所以只需要判断每个陨石的矩形与轨迹矩形有没有重叠即可,判断逻辑参考代码
#include <iostream>
using namespace std;int main() {int a, b;cin >> a >> b;int l, u, r, d;cin >> l >> u >> r >> d;int n;cin >> n;while (n--) {int li, ui, ri, di;cin >> li >> ui >> ri >> di;if (ri >= r && li <= a && !(u < di || d > ui)) {cout << "wuwuwu";return 0;}}cout << "hahaha";return 0;
}J 输出n个不行
#include <bits/stdc++.h>
using namespace std;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n;cin>>n;while(n--){cout<<"buxing\n";}return 0;
}