【研究生随笔】Pytorch中的卷积神经网络（1）

卷积神经网络（convolutional neural network， CNN）：一种主要针对图像数据的强大的神经网络，除了在获得精确模型的采样效率外，卷积神经⽹络在计算上也是极其⾼效的。这是因为卷积神经⽹络需要的参数⽐多层感知机少，而且卷积神经⽹络很容易在GPU上并⾏计算。所以在对于一维序列化结构的任务（音频、文本等）也经常使用到卷积神经网络。
• 从全连接层到卷积
之前讲到的多层感知机就是一种全连接层网络（无结构网络），多层感知机对于处理表格数据来说非常合适，表格数据的每一行代表着一个样本，每一列代表着一个特征。但是，对于高维感知数据（彩图、视频等）便不太适合了（因为一张图片的像素量都是比较高的，除非马赛克 (＠_＠😉 每个像素相当于一个参数，想想看，需要处理很久）。
⼈类视觉和传统机器学习模型都能很好地区分猫和狗。这是因为图像中有丰富的结构，⼈类和机器学习模型都可以利⽤这些结构。卷积神经⽹络是机器学习利⽤⾃然图像中⼀些已知结构的创造性⽅法。

• 不变性：
  想象⼀下，你想对⼀张图⽚中的物体进⾏检测。合理的做法是，我们使⽤的⽆论哪种⽅法都应该和物体的位置⽆关。虽然猪通常不在天上⻜，⻜机通常不在⽔⾥游泳，我们仍然应该意识到猪有可能出现在图⽚的上⽅。卷积神经⽹络正是将“空间不变性”的这⼀概念系统化，⽤较少的参数来学习有⽤的特征。
  -平移不变性：不管出现在图像中的哪个位置，神经⽹络的底层应该对相同的图像区域做出类似的响应。这个原理即为“平移不变性”。
  -局部性：神经⽹络的底层应该只探索输⼊图像中的局部区域，而不考虑图像远处区域的内容，这就是“局部性”原则。最终，这些局部特征可以融会贯通，在整个图像级别上做出预测。
  -限制多层感知机：假设以⼆维图像 X 作为输⼊，那么多层感知机的隐藏表⽰ H 在数学上是⼀个矩阵，在代码中表⽰为⼆维张量。其中 X 和 H 具有相同的形状。那么可以认为，不仅输⼊有空间结构，隐藏表⽰也应该有空间结构。
  ⽤[X](I,j)和[H](i,j) 分别表⽰输⼊图像和隐藏表⽰中位置(i, j)处的像素。为了使每个隐藏神经元都接收到每个输⼊像素的信息，将参数从权重矩阵（如同先前在多层感知机中所做的那样）替换为四阶权重张量 W。假设 U 包含偏置参数，所以可以将全连接层表⽰为：
  
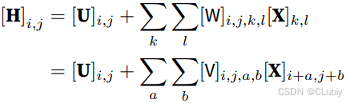
  从 W 到 V 的转换只是形式的转换，因为在两个四阶张量中，系数之间存在⼀⼀对应的关系。所以只需重新索引下标 (k，l)，使 k = i + a、 l = j + b，由此 [V]I,j,a,b = [W]I,j,i+a,j+b。这⾥的索引 a 和 b 覆盖了正偏移和负偏移。对于隐藏表⽰中任意给定位置（i, j）处的像素值[H]I,j，可以通过对 x 中以 (I, j) 为中⼼的像素进⾏加权求和得到，权重为 [V]I,j,a,b。
  使用平移不变性：输⼊ X 中的移位，应该仅与隐藏表⽰H 中的移位相关。也就是说，V 和 U 实际上不依赖于 (i，j) 的值，即 [V]I,j,a,b = [V]a,b。并且 U 是⼀个常数，⽐如 u。因此，可以简化 H 定义为：
  
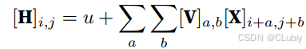
  使用局部性：为了收集⽤来训练参数 [H]I,j 的相关信息，所以不应偏离到距 (I, j) 很远的地⽅。这意味着在 |a| > ∆ 或 |b| > ∆ 的范围之外，我们可以设置 [V]a,b = 0。由此，我们可以将参数 [H]I,j 重写为:
  
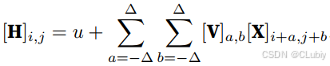
  卷积神经⽹络是包含卷积层的⼀类特殊的神经⽹络。在上面的例子中V被称为卷积核（convolution kernel）或者滤波器（filter），是可学习的权重。当图像处理的局部区域很小时，卷积神经⽹络与多层感知机的训练差异可能是巨⼤的：多层感知机可能需要数⼗亿个参数来表⽰，而现在卷积神经⽹络通常只需要⼏百个参数，而且不需要改变输⼊或隐藏表⽰的维数。参数量的这⼀减少所付出的代价就是，所用的特征现在必须是平移不变的，且每⼀层只能包含局部的信息。以上所有的权重学习都依赖于归纳偏置，当这种偏置与实际情况相符时，就可以得到有效的模型，这些模型能很好地推⼴到不可⻅的数据中。但如果这些假设与实际情况不符，⽐如当图像不满⾜平移不变时，模型可能难以拟合。
• 卷积：在数学中，两个函数之间的卷积是这样定义的：存在f和g属于R^n，（f*g）（X）= ∫_ ^ ▒f(z)g(x−z)dz(对z求积分嘛)，也就是说卷积是测量 f 和 g 之间（把其中⼀个函数“翻转”并移位 x 时）的重叠。
• 通道（channel）：图像⼀般包含三个通道/三种原⾊（红⾊、绿⾊和蓝⾊）。实际上，图像不是⼆维张量，而是⼀个由⾼度、宽度和颜⾊组成的三维张量，⽐如包含 1024 × 1024 × 3 个像素。前两个轴与像素的空间位置有关，而第三个轴就是像素在每个色层的表示。由于输⼊图像是三维的，所以隐藏表⽰ H 也最好采⽤三维张量。换句话说，对于每⼀个空间位置，需要采⽤⼀组而不是⼀个隐藏表⽰。这样⼀组隐藏表⽰可以想象成⼀些互相堆叠的⼆维⽹格。因此，可以把隐藏表⽰想象为⼀系列具有⼆维张量的通道。这些通道有时也被称为 特征映射（feature maps），因为每个通道都向后续层提供⼀组空间化的学习特征。直观上，可以想象在靠近输⼊的底层，⼀些通道专⻔识别边界，而其他通道专⻔识别纹理。
• summary：
  -图像的平移不变性使我们可以以相同的⽅式处理局部图像。
  -局部性意味着计算相应的隐藏表⽰只需⼀小部分局部图像像素。
  -在图像处理中，卷积层通常⽐全连接层需要更少的参数。
  -卷积神经⽹络（CNN）是⼀类特殊的神经⽹络，它可以包含多个卷积层。
  -多个输⼊和输出通道使模型在每个空间位置可以获取图像的多⽅⾯特征。

• 卷积运算其实是互相关运算（cross-correlation），在卷积层中，输⼊张量和核张量通过互相关运算产⽣输出张量。来个例子就有点好明白具体的工作方式了：

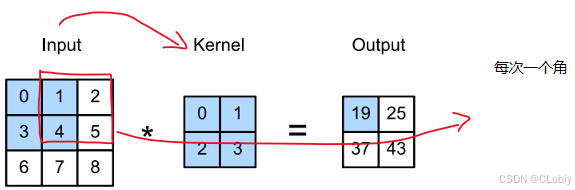
这是一个⼆维互相关运算。阴影部分是第⼀个输出元素，以及⽤于计算这个输出的输⼊和核张量元素： 0×0 +1 × 1 + 3 × 2 + 4 × 3 = 19。
输出⼤小略小于输⼊⼤小。这是因为卷积核的宽度和⾼度⼤于1，而卷积核只与图像中每个⼤小完全适合的位置进⾏互相关运算。所以，输出⼤小等于输⼊⼤小 n_h × n_w 减去卷积核⼤小 k_h × k_w

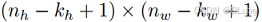
创建一个函数来实现上面的二维互相关运算：

import torch
from torch import nn as nn
from d21 import torch as d21
def Mycross_correlation(X,k): # X为input,K为kernel'''计算二维互相关运算'''h,w = k.shape # 也就是K这个张量的高和宽# 构造一个存储结果的张量，也就是图中的outputY = torch.zeros((X.shape