RL + LLM 强化学习 + 大模型微调 (PPO + GRPO)
目录
0. 大模型微调与强化学习基础
1. PPO(Proximal Policy Optimization) 近端策略优化
1.1 A2C潜在的不稳定因素 & 解决措施
1.2 广义优势估计 GAE
1.3 梯度裁剪
1.4 KL 散度惩罚
2. GRPO 组相对策略优化
3. 蒸馏+拒绝采样
0. 大模型微调与强化学习基础
先SFT后 使得模型具备获得有效奖励的能力;
(否则开始模型 怎么回答都错 价值都是0 没有更新梯度)
1. RLHF 基于人类反馈的强化学习
先收集人类对模型多个回答的排序数据,训练一个 RM 奖励模型。
使用训练好的 RM作为奖励信号,通过强化学习优化SFT模型。
2. DPO 直接偏好优化
直接输入 什么是好回答,什么是坏回答。(不用 RM 奖励模型)
通过巧妙的损失函数,直接优化模型,
使得模型分配给“好回答”的概率与分配给“坏回答”的概率之间的差值最大化。
3. RLVR 基于人类“价值”反馈的强化学习 -> 打击大模型幻觉
传统的RLHF优化的是“看起来好”的回答(有帮助、无害),但模型仍然可能“自信地”编造事实(幻觉)。RLVF旨在让模型对自己不知道或不确定的事情保持诚实。
RM -> 训练一个能判断模型回答是否“诚实”的VM。
VM训练:模型生成一个回答,并附上其引用的来源/证据。
标注员的任务是判断“基于这个证据,模型给出的回答是否被充分支持”。
让标注员去验证模型回答中的事实。
强化学习训练回顾:
1. REINFORCE / 蒙特卡洛策略梯度
Reinforce方法理论
先试玩一把得到轨迹,并倒过来算出每步的reward累积u作为q。
-
无偏性:因为
G_t使用的是环境返回的真实奖励,不依赖于任何估计,所以是无偏的。 -
高方差:由于智能体在环境中的交互本身具有随机性,一条完整的轨迹可能包含很多“运气”成分,导致不同轨迹的
G_t差异很大。用这种波动大的值来更新,会导致训练不稳定。
2. TD误差 / A2C
TD训练
它用了一步即时奖励 r_t 和 对下一状态的价值估计 V(s_{t+1}) 来评估当前动作。
![]()
-
低方差:只关注一步的即时奖励,后续的影响由已经训练过的价值网络
V来概括,因此目标的波动性较小。 -
有偏性:因为
V(s_{t+1})是网络估计出来的,如果这个估计不准,那么整个优势估计就是有偏的。
1. PPO(Proximal Policy Optimization) 近端策略优化
1.1 A2C潜在的不稳定因素 & 解决措施
1. 时序差分 TD 偏差。
TD学习是Critic网络的核心训练方法。它用一个估计值去更新另一个估计值。
这面临 “自举” 的问题 用一个自身的、或者正在学习的估计值,去更新另一个估计值。
后面的 V(s') 被高估,导致前面的 V(s) 被高估,还要拿 V(s) 去更新别人。 导致偏差累积更大。
解决方案:
-
目标网络:使用一个更新较慢的“目标网络”
V_target(s')来计算TD Target。这能在一定时间内提供一个相对稳定的目标,打破不稳定的正反馈循环。这也是DQN和DDPG等算法的核心思想。(异策略 off-policy)
TD_target = r + γ * V_target(s') -
多步TD:使用多步回报来减少对单个有偏估计
V(s')的依赖,例如使用n步TD Target:TD_target = r_t + γ * r_{t+1} + ... + γ^n * V(s_{t+n})。这用更多来自环境的真实奖励(无偏)来稀释最终的价值估计(有偏)。
2. 行为策略和目标策略差异过大则会训练不稳定。
off - policy 异策略:如何用行为策略Q(过去)准确估计目标策略P(新)的性能。
重要性采样:为样本乘以 P(x) / Q(x) 的权重,去修正两个分布的差异。
(但还是需要 新旧策略差异不太大)
1.2 广义优势估计 GAE
(MC和TD中间点 平衡方差和偏差)
问题:为了更新Actor,我们需要知道每个动作的好坏,即优势函数 A(s, a)。
用动作价值减去本身的状态价值 A(s, a) = Q(s, a) - V(s)。但Q值很难精确获得。
解决方法:GAE提供了一种高效、低偏差且低方差的优势估计方法。
-
蒙特卡洛:使用整个回合的真实回报
G_t来估计。无偏,但高方差(因为后续所有随机动作和状态转移的噪声都包含在内)。 -
时序差分:使用一步奖励和下一个状态的估计值
r + γV(s') - V(s)。低方差,但有偏(因为V(s')可能不准)。
GAE的智慧:将N步TD回报进行指数加权平均,取一个中间点。
广义优势估计在时间步 t 的计算公式为:
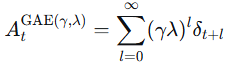
其中 δ_t = r_t + γV(s_{t+1}) - V(s_t) 是TD误差。
-
λ=0:则
A_t = δ_t,退化为纯TD方法,低方差但有偏。 -
λ=1:则
A_t = G_t - V(s_t),退化为蒙特卡洛方法,无偏但高方差。
通过调节 λ(通常取0.9-0.99),我们可以在偏差和方差之间取得一个优秀的平衡,从而得到更平滑、更可靠的优势估计。
1.3 梯度裁剪
限制新策略 π_θ 与旧策略 π_θ_old(用于收集数据的策略)差异不会超过 ε 。
概率比:![]()
不加限制地最大化 r_t(θ) * A_t 会导致策略剧烈变化。
PPO引入了裁剪操作:差异上下界 1 ±ε
![]()
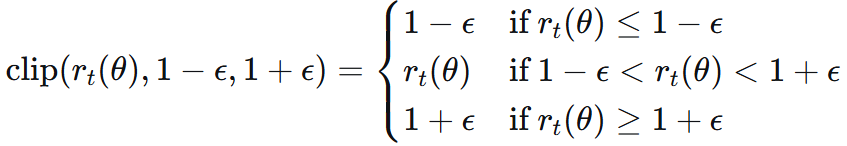
无论一个动作看起来有多好或多坏,PPO都禁止策略在一次更新中对其概率进行剧烈的改变。
1.4 KL 散度惩罚
前身TRPO:把 KL 散度作为一个约束条件。这会使得问题难以求解。
PPO 在优化目标 r_t(θ) * A_t 中直接添加一个惩罚项,用于惩罚新旧策略之间的KL散度。
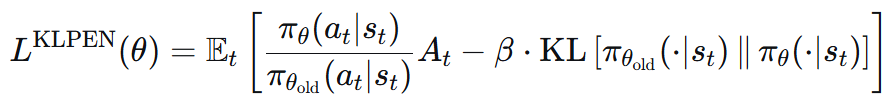
最终训练时就需要四个模型:
1. Actor (演员) - 策略模型 π_θ 2. Critic (评论家) - 价值模型 V_φ(s)
3. Reward (奖励) - 奖励信号 R 4. Reference (参考) - 参考模型 π_ref
2. GRPO 组相对策略优化
在PPO中,优势函数 A(s, a) 衡量的是在状态 s 下执行动作 a 相对于该状态的平均水平好多少。
这个“平均水平”由Critic模型 V(s) 给出。
而 GRPO 移除了价值网络(critic)
在大语言模型中,我们很难也不必要知道一个生成长度不一的序列的绝对价值是多少。我们只需要知道,在同一组(同一个提示词下生成的多个回答) 里,哪个回答更好,哪个更差就足够了。
因此,GRPO的优势估计是组内相对的。于是,可以用一组轨迹的组内平均值作为基线。
它用 “组内平均得分” b 替代了 PPO中Critic 预测的 “状态价值” V(s)。
用 RM(x, y) - mean(RM(x, y_group)) ,实现了与PPO的 G_t - V(s) 相似的功能。
并使用:组内奖励归一化,进一步降低方差。
优势:使得训练效率提高,更稳定;组内排序机制 吻合 优化相对偏好。
3. 蒸馏+拒绝采样
教师模型(Teacher Model) 是已经训练好的、性能强大的复杂模型,这里是 DeepSeek-R1。
学生模型(Student Model) 则是待训练的小模型,例如 Qwen2.5 或 Llama 系列的模型。
拒绝采样:从教师模型生成的大量候选答案中,筛选出高质量推理数据(答案对且格式清晰)
把这部分数据以及思维链,喂给学生模型,实现小参数量实现高性能。
