当前位置：首页 > news >正文

基于Matlab的批处理最小二乘法参数估计

news 2025/10/29 8:59:24

文章目录

前言
一、最小二乘法参数估计？
二、数理前提。
三、示例数理运算。
四、Matlab代码实现。
五、结果分析。
总结

前言

本文是对学习系统辨识的一个记录，因为也是初学者，很多理论会以通俗的个人理解加以描述，这样便于理解，但是会缺失一些严谨性，故合理参考。
本文会简单讲述什么是批处理最小二乘法参数估计，然后基于一个示例用Matlab完成这个示例的参数估计验证，会讲解Matlab语句的用法和代表的矩阵运算机理。非常适合入门。

一、最小二乘法参数估计？

最小二乘法参数估计（Least Squares Parameter Estimation）是一种通过最小化 “观测值与模型预测值之间误差的平方和” 来估计系统未知参数的数学方法。
通俗理解就是有一个系统模型，我能大致确定他的机理，能确定系统的传递函数，但传递函数的每一个环节的参数无法确定，此时利用该系统的输入输出值带入最小二乘法参数估计来估计出传递函数中的每一个位置的参数。这么说是不是就一下理解了，那本文用的批处理就是最小二乘法参数估计中的一种估计方法。

二、数理前提。

比如有一个离散模型
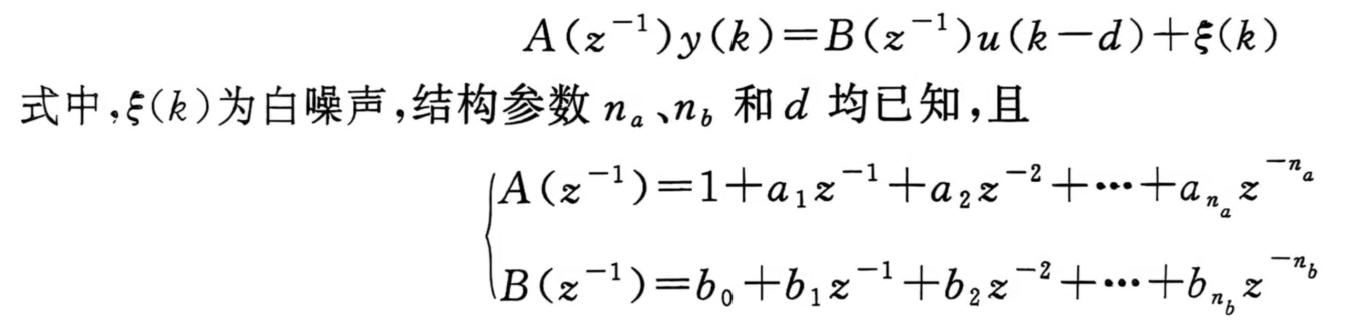
在这里插入图片描述
其中白噪声可以看成一个扰动。现在就是要记录u(0)、y(0)；u(1)、y(1)；u(2)、y(2)；u(3)、y(3)；…然后通过这些数据把模式中两个传递函数所有的未知值a1、a2、a3、…、a(na)；b0、b1、a2、…、a(nb)个参数估计出来，就完成了。
那么批处理的估计计算公式如下
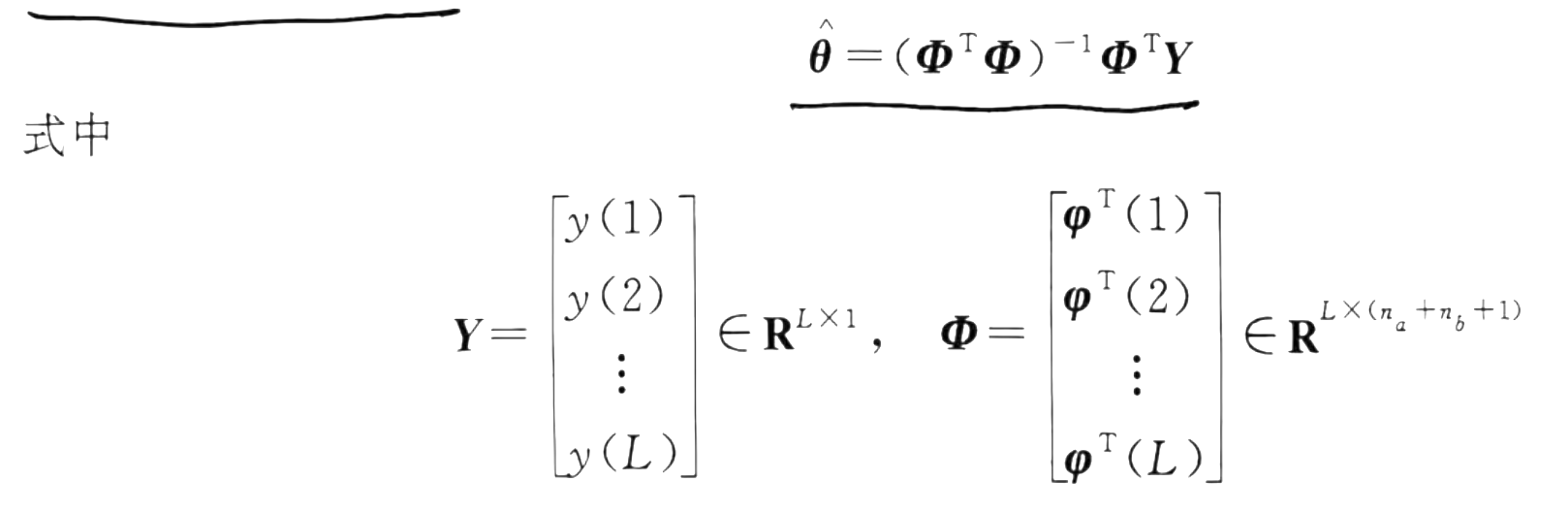
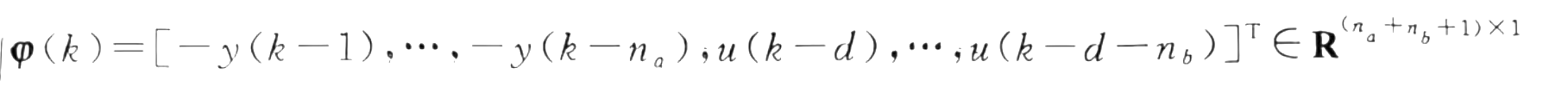
在这里插入图片描述

最后求得的结果如下，刚好是所有的待确定参数。

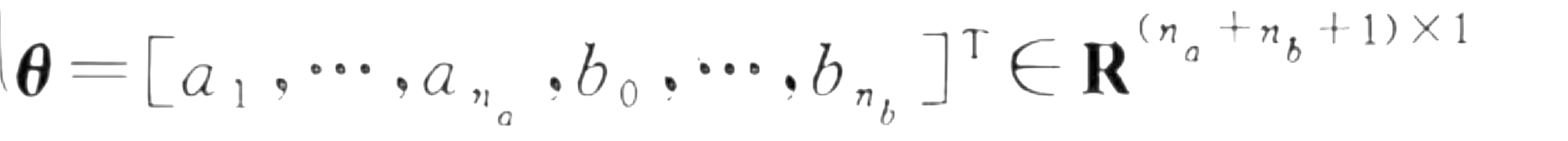
三、示例数理运算。

现在给出一个具体的系统的差分方程表达式如下：
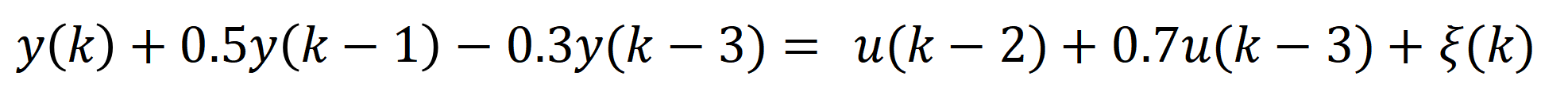
在这里插入图片描述
离散系统传递函数转换为差分方程很简单，不解释了。
写成矩阵运算形式如下：

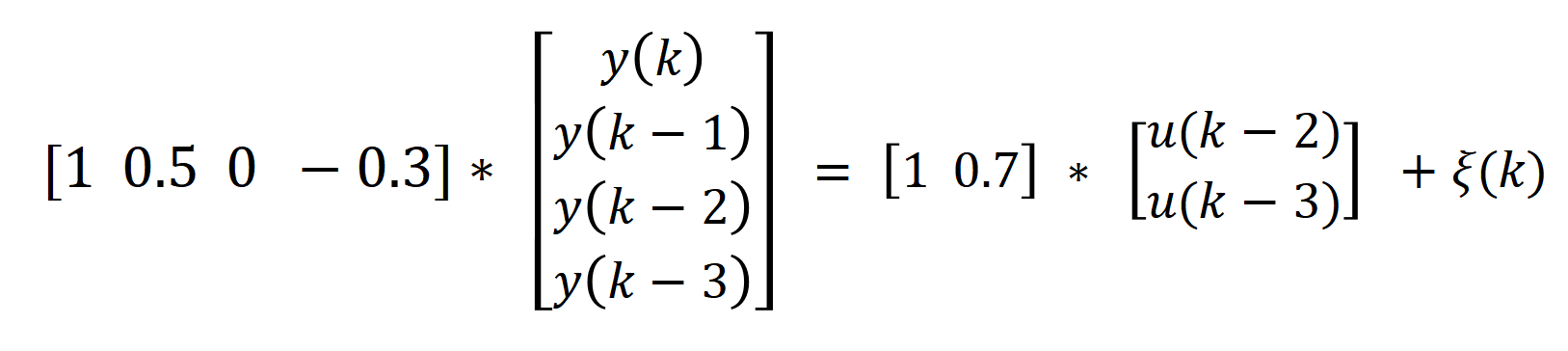
比较一下可知a1 = 0.5；a2 = 0；a3 = -0.3；b2 = 1；b3 = 0.7；其他参数都是0。根据φ(k)表达式计算出na = 3；nb = 1； d = 2

那参数都有了，我还估计啥。而且最小二乘法参数估计是需要输入输出值已知的，我们有不是真有这么一个系统，那输入输出值从何而来？是不是有这个疑问。
我们处理是这样的，通过我们给定的输入值，然后通过该差分方程计算出输出值，然后利用最小二乘法参数估计去估计参数。理论上如果ξ(k) = 0，也就是没有扰动，那么最小二乘法参数估计值和该差分方程的参数应该是一样的才能验证出最小二乘法参数估计法的正确性。相当于走了一个闭环。我们接下来就是验证批处理最小二乘法参数估计的正确性，理解了，就可以继续了。

四、Matlab代码实现。

clear;
A = [1 0.5 0 -0.3];
B = [1 0.7];
d = 2;
na = length(A) - 1; %3
nb = length(B) - 1; %1

一步步来，先clear清楚历史记录。再把A，B矩阵表示出来，都是行向量，再把确定的na、nb、d这些值赋值。不建议直接赋值成常量，这样缺失了通用性。

L = 100;
uk = zeros(d+nb, 1);
yk = zeros(na, 1);  
Xi = [0 1 1 1]; S = 1;
white_noise = randn(1,L);

第二步，L的意义先不讲，行向量uk就是输入，含义如下，可知当k = 0时，uk是零行向量（零时刻前的输入都是0，故输出也是0）
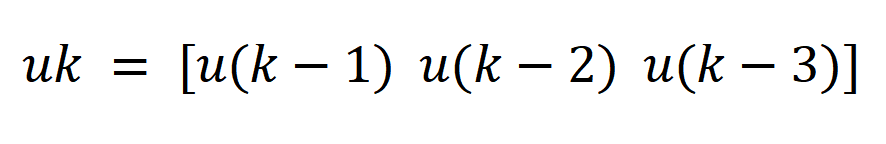
在这里插入图片描述
行向量yk就是输出，含义如下，可知当k = 0时，yk是零行向量

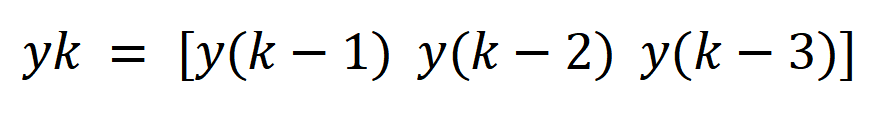
从而完成了φ(k)的表达

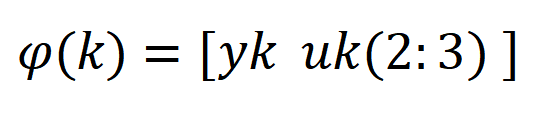
接下来0时刻后的输入怎么选呢，工业上常用一个逆M序列作为输出，Xi行向量和S是用来生成这个逆M序列的，这里不解释。
white_noise 是100个随机正态分布数列用来模拟扰动ξ(k)。

theta = [A(2:na+1) B]';
phi = zeros(L, na+nb+1);
y = zeros(L, 1);
for k = 1:Lphi(k,:) = [-yk; uk(d: d+nb)];y(k) = phi(k,:) * theta + white_noise(k);M = xor(Xi(1),Xi(2));for i = 1:3Xi(i) = Xi(i+1);endXi(4) = M;IM = xor(M, S);S = not(S);if IM == 0u1 = -1;elseu1 = 1;endfor i = d+nb:-1:2uk(i) = uk(i-1);enduk(1) = u1;for i = na:-1:2yk(i) = yk(i-1);endyk(1) = y(k);
end
thetae = inv(phi' * phi) * phi'*y

化简的y(k)表达式如下。theta 列向量就是[0.5 0 −0.3 1 0.7]T，创建一个100行，5列的零矩阵phi用来储存Φ。运用批处理法公式有一个前提条件就是矩阵Φ必须满秩，那么只要我计算的输出足够多就一定会满秩，所以L = 100，表示将会运算100个输出。
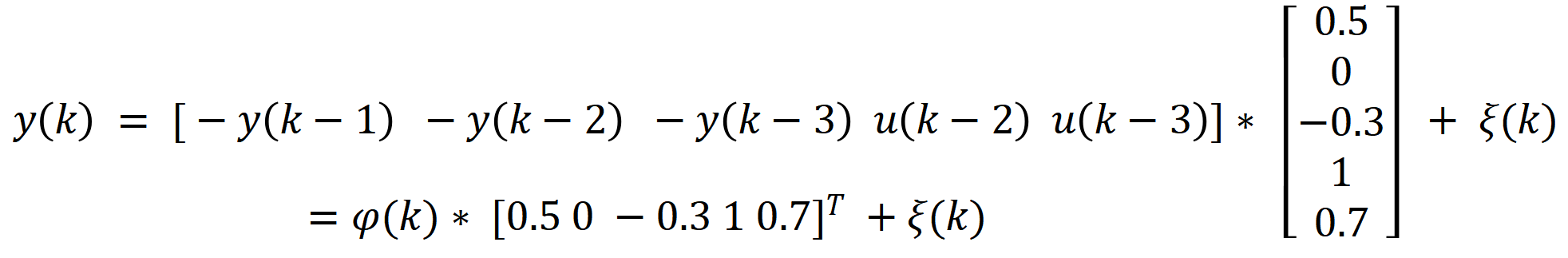
在这里插入图片描述
主for循环内的函数就不讲解了，不好说清楚，大致内容就是根据逆M序列计算出下一时刻的输入u1和根据公式计算出下一时刻的输出y(k)，然后更新向量uk和yk，从而计算出矩阵Φ用phi表示和输出向量y。
最后根据公式thetae = inv(phi' * phi) * phi'*y计算出批处理最小二乘法参数估计值。
完整代码如下：

clear;A = [1 0.5 0 -0.3];
B = [1 0.7];
d = 2;
na = length(A) - 1; %3
nb = length(B) - 1; %1L = 100;
uk = zeros(d+nb, 1);
yk = zeros(na, 1);  
Xi = [0 1 1 1]; S = 1;
white_noise = randn(1,L);theta = [A(2:na+1) B]';
phi = zeros(L, na+nb+1);
y = zeros(L, 1);
for k = 1:Lphi(k,:) = [-yk; uk(d: d+nb)];y(k) = phi(k,:) * theta + white_noise(k);M = xor(Xi(1),Xi(2));for i = 1:3Xi(i) = Xi(i+1);endXi(4) = M;IM = xor(M, S);S = not(S);if IM == 0u1 = -1;elseu1 = 1;endfor i = d+nb:-1:2uk(i) = uk(i-1);enduk(1) = u1;for i = na:-1:2yk(i) = yk(i-1);endyk(1) = y(k);
end
thetae = inv(phi' * phi) * phi'*y

五、结果分析。

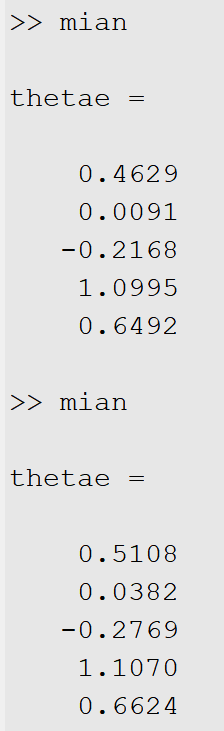
通过Matlab运行代码得到结果如下
在这里插入图片描述
每次运行结果会略有不同，这是因为有扰动ξ(k)存在

现在令ξ(k) = 0，也就是把y(k) = phi(k,:) * theta + white_noise(k);这句的white_noise删除得
y(k) = phi(k,:) * theta ，那么得到的参数估计值就应该是给定值，运行代码如下
在这里插入图片描述
通过比较参数估计值等于给定值，证明得批处理最小二乘法参数估计结果合理且成立