吴恩达DeepLearning课程我的笔记week2
2.1 二分类(Binary Classification)
一些符号和概念处理
训练集什么样
将一张图片的所有像素提取出来
64x64像素大小图片获得三个规模为64x64的矩阵,R、G、B
因此训练集高度为64*64*3=12288
记录为,它就是接下来数据集的高度,我们也称为特征向量x的维度
有多少训练样本比如m个,则训练集矩阵X为下图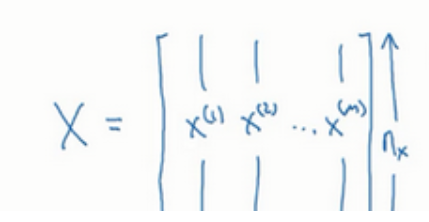
当然有时候是行堆叠起来而不是列,怎么简单怎么来但一般,像我们这样搞
训练集与python
X.shape用于显示矩阵规模
输出标签
大写Y等于右侧
规模是1 x m
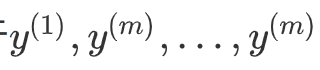
python表示为Y.shape
好符号很重要,而且要记着都啥意思
2.2 逻辑回归(Logistic Regression)
Hypothesis Function假设函数
我们想要一个算法能够输出预测X图片是不是猫
首先是线性回归用到的这个公式,w这里是和x同维度的特征权重
但用在这里不是很合适,因为^y应该在0到1之间,而这个式子可能为负或者比1大得多
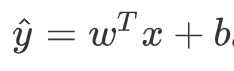
sigmoid函数
因此我们可以使用sigmoid函数
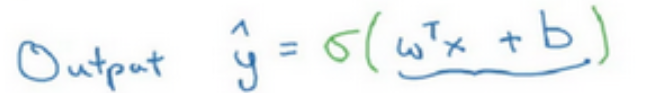
实际上是将线性函数转化为了非线性函数
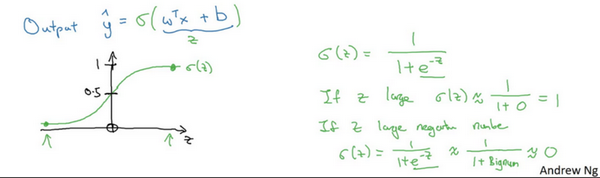
图像如上图,sigmoid函数平滑地从0走向1,曲线与纵轴相交的截距是0.5
我们通常用z来代表w^T x+b的值,看上图右侧公式
z很大——sigmoid函数非常接近1
z很小/是绝对值很大的负数——sigmoid函数非常接近0
我们要做的就是尽量使得^y像y,值靠近1
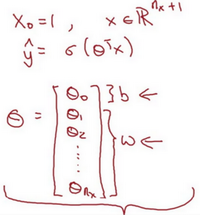
符号惯例
当我们对神经网络进行编程时经常会让参数w和参数b分开,在这里参数b对应的是一种偏置
2.3 逻辑回归的代价函数(Logistic Regression Cost Function)
为什么需要代价函数:
为了训练逻辑回归模型的参数w和参数b,我们需要一个代价函数

(上式子是对于一个训练样本来说,上标(i)代表第i个训练样板)
损失函数:
又叫误差函数,loss function.
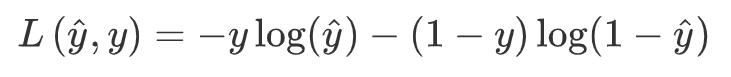
在逻辑回归中我们一般公式如上右图所示,其他地方有时会采用预测值和实际值的平方差或者它们平方差的一半
如果y等于1,我们就尽可能让^y变大,如果y等于0,我们就尽可能让^y变小
这是算法在单个样本的表现,接下来是总代价
我们想要的是代表函数J的总代价min时的w和b
⚠️这里的log代表的就是ln只是省略了,默认为ln
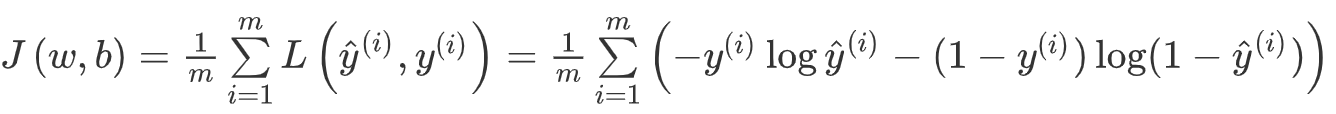
逻辑回归可以看作是一个非常小的神经网络
2.4 梯度下降法(Gradient Descent)
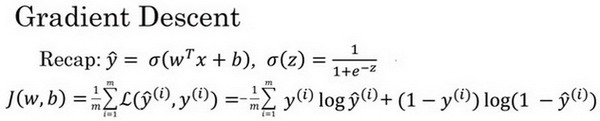
在图中,横轴代表空间参数w,b(实践中w可以是更高维度这里为画图方便未展示)
代价函数J(w,b)为曲面,高度为函数值
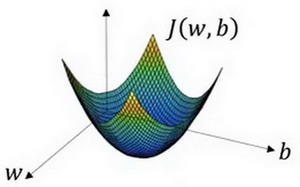
同时我们记得代价函数J(w,b)是一个凸函数(convex function),否则会非凸并有多个局部最小值


红点的位置代表初始化,由于凸函数,在哪里是无所谓的,因为大概都能到最小值,可以采用随机等方式
如图,红点向下走迭代,直到走到全局最优解或者接近全局最优解的地方
此时就是J(w,b)的最小值点
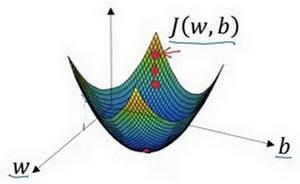
迭代就是重复图中的公式
:=代表更新参数
α代表学习率,用于控制每次向下走的步长,如最右侧图,(步长是a右边那个dJ(w)/dw,或者说斜率)
在代码中dw表示步长
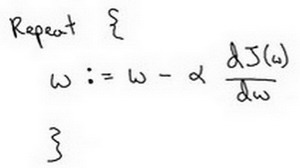
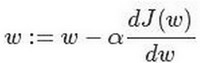

逼近最低点就是整个梯度下降法的迭代过程
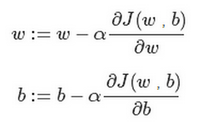
 round
round
小写字母d用在求导数(derivative),即函数只有一个参数, 偏导数符号round用在求偏导(partial derivative)即函数含有两个以上的参数
2.5&2.6 导数(Derivatives)

导数就是斜率,而函数的斜率,在不同的点是不同的
注意一点,导数增大的值,不是刚好等于导数公式算出来的值,而只是根据导数算出来的一个估计值
2.7 计算图(Computation Graph)

J是由a,b,c三个变量组成的函数,这个函数是3(a+bc)
见图上三步走(高中学过,导数时候的链式法则)
计算图组织计算的形式是用蓝色箭头从左到右的计算,让我们看看下一个视频中如何进行反向红色箭头(也就是从右到左)的导数计算
2.8 使用计算图求导数
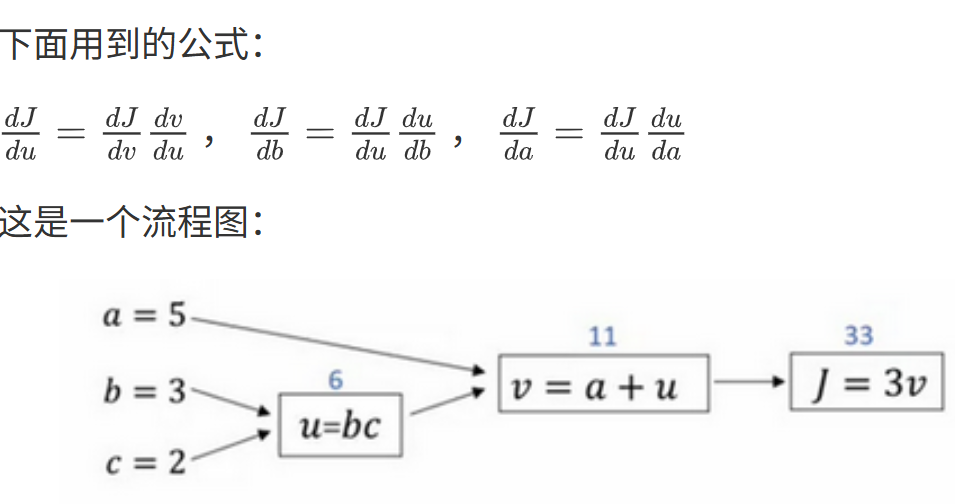
这里的反向传播指的是:当改变一个值(例如u),求的dJ/du = dJ/dv * dv/du 这样从最终往前面的流程推得到结果(当计算所有这些导数时,最有效率的办法是从右到左计算)
符号约定:
编程实现反向传播时,通常会有一个最终输出值是你要关心的
在这种情况下最终的输出变量是J(有时候为L...),就是流程图里最后一个符号
输出变量对某个变量的导数,我们就用dvar命名,比如dJ_dvar
2.9 逻辑回归中的梯度下降(Logistic Regression Gradient Descent)
如何用偏导数来实现逻辑回归的梯度下降算法
回忆一下
线性组合公式
逻辑回归公式
,其中
损失函数
$
代价公式
参数更新公式(梯度下降)

计算图就是好,不用再写公式了
反向计算导数
最后进行反向推导,计算w,b对L的影响(梯度下降参数更新)
单个样本梯度下降参数更新一次
上面dw1表示图1,dw2基本相同
db = dz
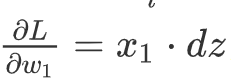
因此我们需要做的:用dz =(a - y)计算dz,用dw1 = x1 * dz计算dw1,dw2
dz计算db,然后更新w1 = w1 - adw1, w2 = w2 - adw2, b = b - adb
以上就是单个样本梯度下降参数更新一次的步骤

2.10 m 个样本的梯度下降(Gradient Descent on m Examples)
时刻记住定义
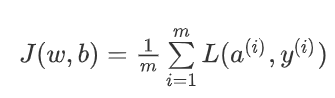
a是训练样本的预测值,可以看到在多样本求的是各个样本损失的平均
在下图你可以看到a的一个链式推导

代码流程
J=0;dw1=0;dw2=0;db=0;
for i = 1 to mz(i) = wx(i)+b;## 这是个激活函数,sigmoid是1/1+e^-z那个a(i) = sigmoid(z(i));J += -[y(i)log(a(i))+(1-y(i))log(1-a(i));dz(i) = a(i)-y(i);dw1 += x1(i)dz(i);dw2 += x2(i)dz(i);db += dz(i);
J/= m;
dw1/= m;
dw2/= m;
db/= m;
w=w-alpha*dw
b=b-alpha*dbfor循环很低效,我们会用向量化技术替代它
2.11 向量化(Vectorization)
代替for,我们可以使用z=np.dot(w,x)+b,速度快

import numpy as np #导入numpy库
a = np.array([1,2,3,4]) #创建一个数据a
print(a)
# [1 2 3 4]
import time #导入时间库
a = np.random.rand(1000000)
b = np.random.rand(1000000) #通过round随机得到两个一百万维度的数组
tic = time.time() #现在测量一下当前时间
#向量化的版本
c = np.dot(a,b)
toc = time.time()
print(“Vectorized version:” + str(1000*(toc-tic)) +”ms”) #打印一下向量化的版本的时间#继续增加非向量化的版本
c = 0
tic = time.time()
for i in range(1000000):c += a[i]*b[i]
toc = time.time()
print(c)
print(“For loop:” + str(1000*(toc-tic)) + “ms”)#打印for循环的版本的时间
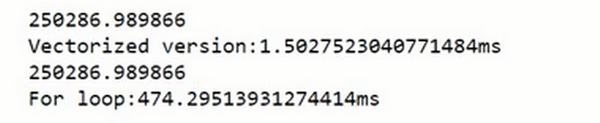
对比发现快多了
2.12 向量化的更多例子(More Examples of Vectorization)
矩阵乘法
下图我们可以两层循环加u=np.zeros((n,1))
当然向量化的更好,直接u=np.dot(A,v)

指数操作
如果你已经有一个向量v,并且想要对向量的每个元素做指数操作
你也可以for循环加np.zeros((n,1))
你也可以用向量化, 用u = np.exp(v)来将v所有元素都指数操作,像是取对数,绝对值,最大值......numpy里面都有,如下图

2.13 向量化逻辑回归(Vectorizing Logistic Regression)
如何用向量化表示我们的线性回归和sigmoid过程

构建1xm矩阵(行向量)用w转置乘m再加上向量[bbb...b]
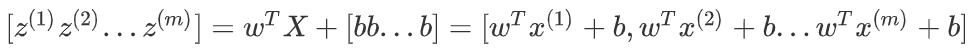
转置是矩阵 / 向量的一种基础操作,核心是“交换行和列的位置”,用符号 “$$^T$$” 表示(比如向量的转置记为
。
上述在numpy表示命令为Z = np.dot(w.T, X)+b
其中b被python自动扩展成一个1xm的行向量
2.14 向量化 logistic 回归的梯度输出(Vectorizing Logistic Regression's Gradient)
dw = 0
dw += x^(1) * dz^(1)
dw += x^(2) * dz^(2)
............
dw += x^(m) * dz^(m)
dw = dw / m
db = 0
db += dz^(1)
db += dz^(2)
............
db += dz^(m)
db = db / m这是目前的循环,我们要将计算dw遍历训练集的过程向量化
对于db,我们知道
则我们可以用db = 1/m * np.sum(dZ)
对于dw,我们知道
,咳,没什么需要变的,很好
此时我们的代码是
# Z = w^T X + b
Z = np.dot(w.T, X) + b
# A = σ(Z)
A = sigmoid(Z)# dZ = A - Y
dZ = A - Y
# dw = (1/m) * X * dZ^T
dw = (1 / m) * np.dot(X, dZ.T)# db = (1/m) * np.sum(dZ)
db = (1 / m) * np.sum(dZ)# w := w - alpha * dw
w = w - alpha * dw
# b := b - alpha * db
b = b - alpha * db我们利用前五个公式完成前向后向传播与对训练样本的预测求导
利用后两个公式梯度下降更新参数
至此,高效的逻辑回归梯度下降算法完结
前向传播:
Z = wT X + b:计算线性输出,w 是权重矩阵,X 是输入特征矩阵,b 是偏置A = o(Z):通过激活函数 o (通常是 sigmoid 或 ReLU) 计算最终输出
反向传播:
dZ = A - Y:计算 Z 的梯度,Y 是真实标签dw = (1/m) * X * dZ^T:计算权重 w 的梯度(原公式中 ÷ 应为 1/m,m 是样本数)db = (1/m) * np.sum(dZ):计算偏置 b 的梯度
参数更新:
w := w - α * dw:用学习率 α 更新权重 wb := b - α * db:用学习率 α 更新偏置 b
2.15 Python 中的广播(Broadcasting in Python)
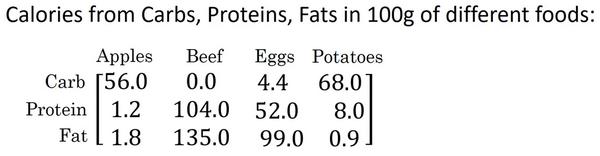
不用for而用numpy,首先对每一列求和

A.sum(axis = 0)中的参数axis。axis用来指明将要进行的运算是沿着哪个轴执行,在numpy中,0轴是垂直的,也就是列,而1轴是水平的,也就是行
然后计算百分比,将原来的3x4的列除以我们得到的“每列和”这个1x4的矩阵
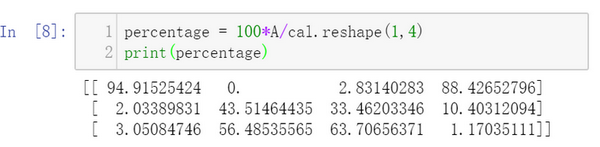
A/cal.reshape(1,4)
调用了numpy的广播机制
其实这里只是举例重塑成1 x 4,因为矩阵本身就是1 x 4了
遇到不确定矩阵维数时通常会重塑矩阵保证想要的
广播机制
比如一个4 X 1的列向量与一个常数做加法时,实际上会将常数扩展为一个4 X 1的列向量

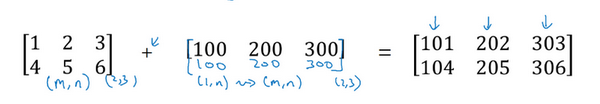
M x n的矩阵和 1 x n的矩阵相加,此时将1 x n复制成m x n,如上图
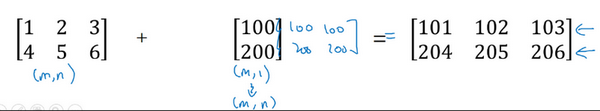

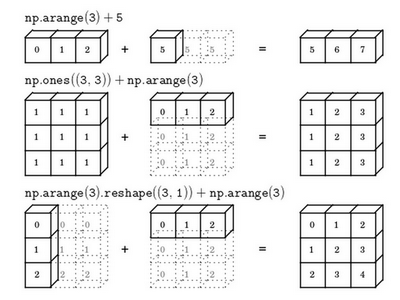
广播机制的一般原则如上图所示
如果两个数组的后缘维度的轴长度相符或其中一方的轴长度为1,则认为它们是广播兼容的。广播会在缺失维度和轴长度为1的维度上进行。
后缘维度的轴长度:A.shape[-1] 即矩阵维度元组中的最后一个位置的值

总结broadcasting
2.16 关于 python _ numpy 向量的说明
一维数组(5, ) (n,)和正常矩阵比,每个数少一个括号
且其转置后看起来还是自己,不变
如何判断是一维数组还是1xn的矩阵?
用断言确定
