【洛谷】高精度专题 加减乘除全实现
文章目录
- 高精度加法
- 高精度减法
- 高精度乘法
- 高精度除法
高精度加法
题目描述
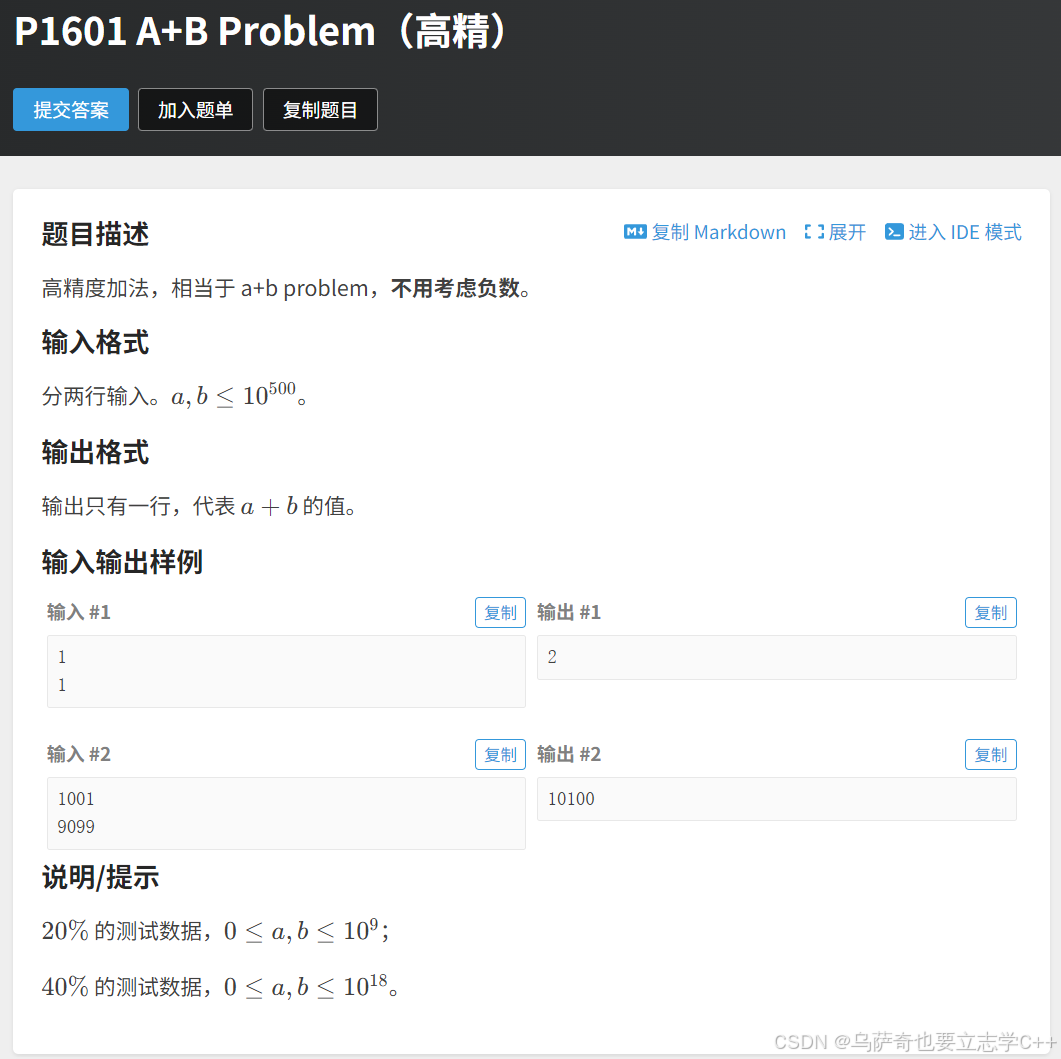
题目解析
当数据的值特别⼤,各种类型都存不下的时候,此时就要⽤⾼精度算法来计算加减乘除:
• 先⽤字符串读⼊这个数,然后⽤数组逆序存储该数的每⼀位;
• 利⽤数组,模拟加减乘除运算的过程。
⾼精度算法本质上还是模拟算法,⽤代码模拟⼩学列竖式计算加减乘除的过程。
下图是用数组逆序存储字符串数据的核心操作:

下面我们来看高精度加法,解题思路分三步走:
1、对应位相加,并加上进位。
2、处理进位,若有进位,直接把进位往高位加。
3、处理余数,把第一步的结果取余,余数为加后对应位结果。
代码
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;const int N = 1e5 + 10;
//分别逆序存储两个加数序列,和加后结果
int a[N], b[N], c[N];
int la, lb, lc; //存储数组有效数据下个数// 高精度加法模板
void add(int a[], int b[], int c[])
{for (int i = 0; i < lc; i++){// 1、对应位相加,然后加上进位,所以需要+=c[i] += a[i] + b[i];// 2、处理进位c[i + 1] += c[i] / 10;// 3、处理余数,余数为最终结果c[i] = c[i] % 10;}//若c[lc]有数据,相当于最高位有进位,需要lc++if (c[lc])lc++;
}int main()
{string x, y;cin >> x >> y;la = x.size(), lb = y.size(), lc = max(la, lb);// 1、将sring中的ASCII字符转换为整数后逆序存入数组for (int i = 0; i < la; i++){a[la - i - 1] = x[i] - '0';}for (int i = 0; i < lb; i++){b[lb - i - 1] = y[i] - '0';}// 2、开始模拟加法add(a, b, c);// 3、输出结果for (int i = lc - 1; i >= 0; i--){//逆序输出cout << c[i];}return 0;
}
高精度减法
题目描述
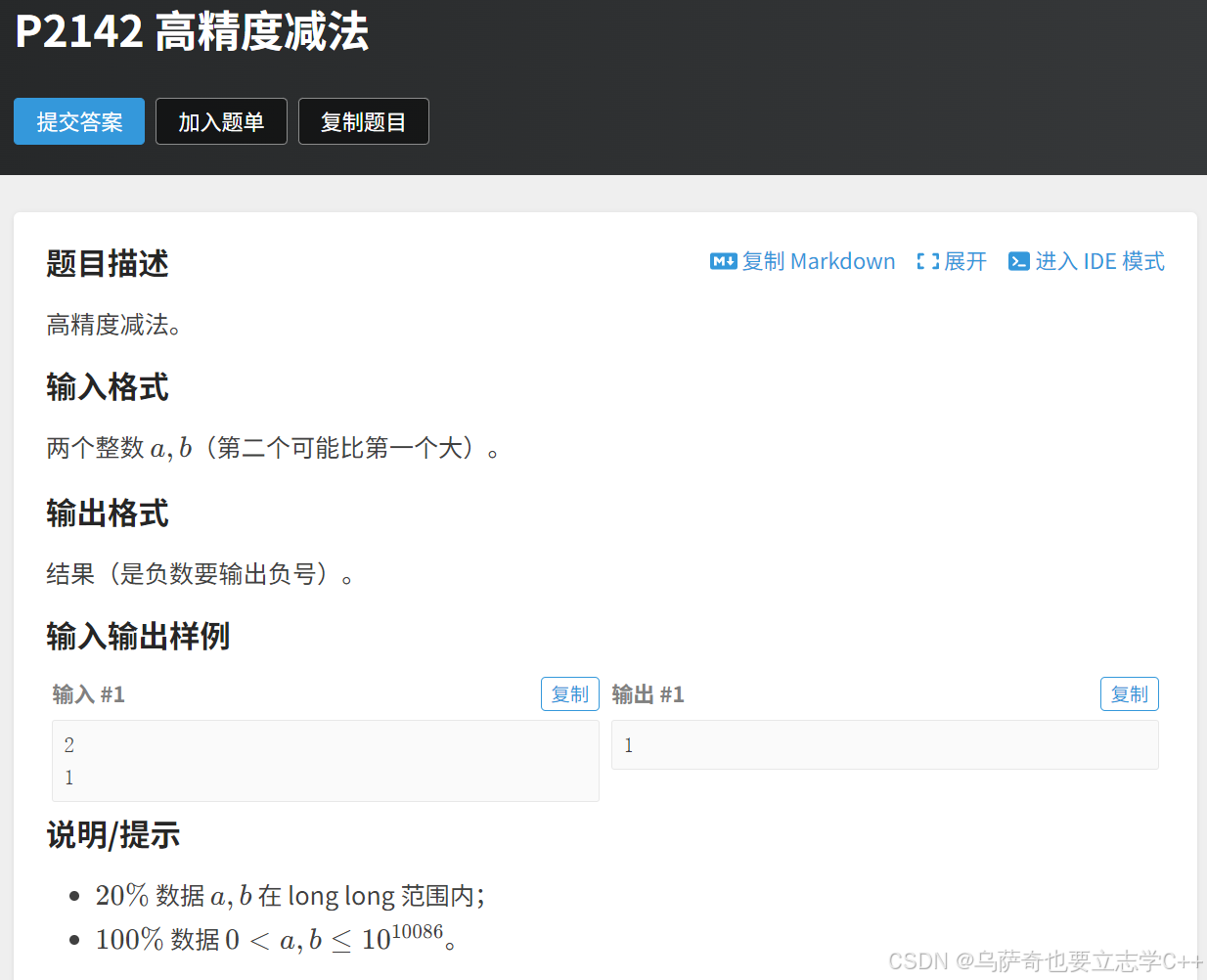
题目解析
本题需要注意几点:
1、题目说是可能出现负数的,所以要先判断减数和被减数哪个更大,比较方法是先比较字符串长度,若字符串长度相同则按字典序比较(string的operator<)。
2、减后结果可能出现前导0,比如9999 - 9998,需要把结果的前三个0跳过,相当于要让原来为4的lc变为1,就需要一直循环判断 c[lc + 1] ,若c[lc + 1]为0则lc–。但lc至少要为1,因为至少要输出一个0。
代码
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;const int N = 1e6 + 10;int a[N], b[N], c[N];
int la, lb, lc;bool cmp(string x, string y)
{if (y.size() != x.size())return y.size() > x.size();return y > x;
}void sub(int a[], int b[], int c[])
{for (int i = 0; i < lc; i++){// 1、对应位相减(有可能c[i]被借位为-1了,所以要+=)c[i] += a[i] - b[i];// 2、处理借位if (c[i] < 0){c[i + 1]--;c[i] += 10;}}// 处理前导零while (lc > 1 && c[lc - 1] == 0){lc--;}
}int main()
{string x, y;cin >> x >> y;la = x.size(), lb = y.size(), lc = max(la, lb);// 比较两个数大小if (cmp(x, y)){swap(x, y);cout << "-";}// 1、将字符数字(ASCII码)转为整数逆序存入数组la = x.size(), lb = y.size(), lc = max(la, lb);for (int i = 0; i < la; i++){ a[i] = x[la - i - 1] - '0';}for (int i = 0; i < lb; i++){b[i] = y[lb - i - 1] - '0';}// 2、subsub(a, b, c); // c = a - b// 3、输出结果for (int i = lc - 1; i >= 0; i--){cout << c[i];}return 0;
}
高精度乘法
题目描述
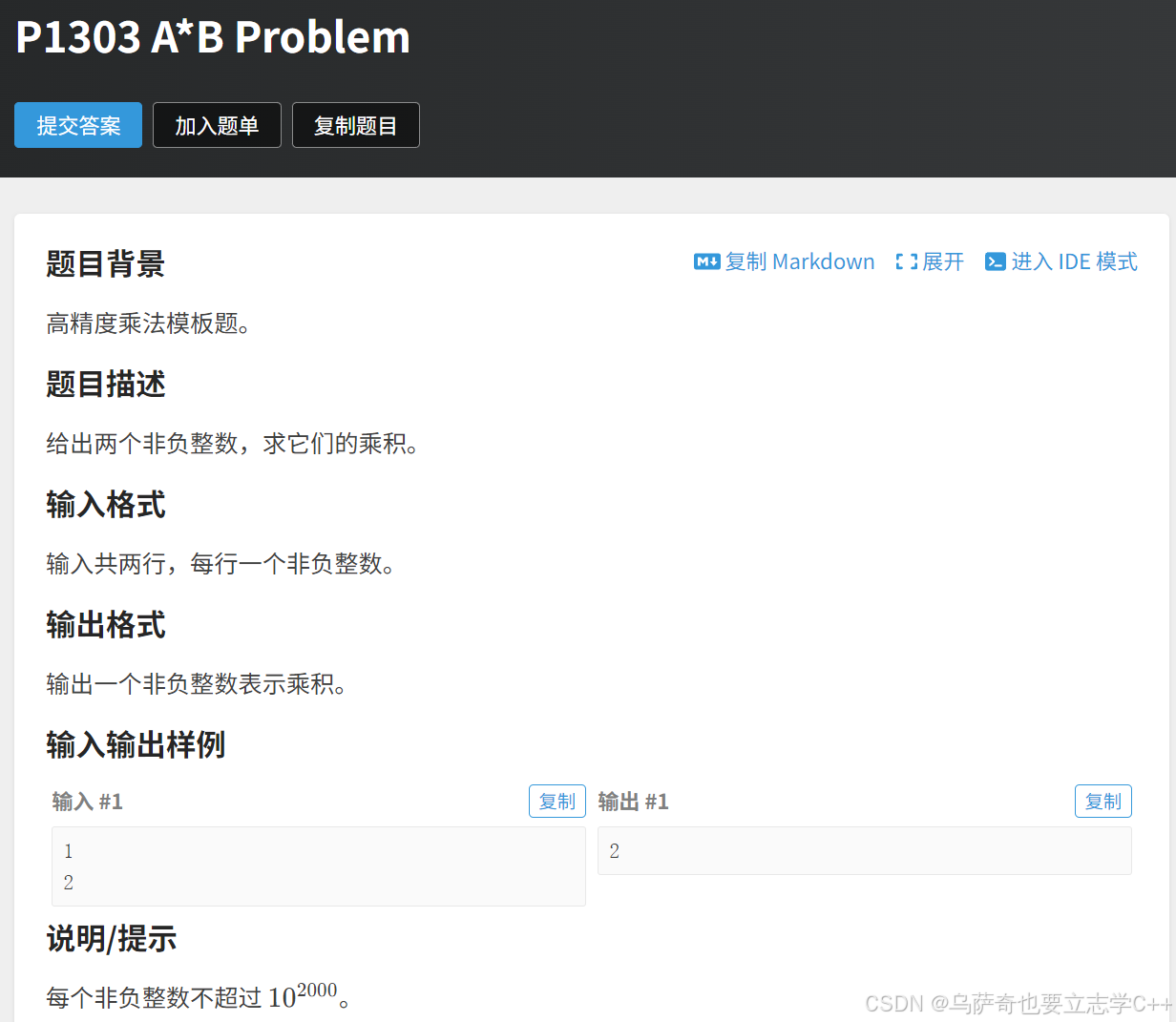
题目解析
本题的核心思路是无进位相乘相加,最后处理进位,如下图:

相乘后的数字在数组c中的下标是两个乘数分别各自在数组a、b中的下标之和。
本题也需要处理前导0。
代码
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;const int N = 1e5 + 10;
const int M = 1e6 + 10;int a[N], b[N], c[M];
int la, lb, lc;void mul(int a[], int b[], int c[])
{// 1、无进位相乘、相加for (int i = 0; i < la; i++){for (int j = 0; j < lb; j++){c[i + j] += a[i] * b[j];}}// 2、处理进位for (int i = 0; i < lc; i++){//下面讲究先后顺序c[i + 1] += c[i] / 10;c[i] %= 10;}// 3、处理前导0while (lc > 1 && c[lc - 1] == 0){lc--;}
}int main()
{string x, y;cin >> x >> y;// 1、提取字符串数据逆序到数组la = x.size(), lb = y.size(), lc = la + lb;for (int i = 0; i < x.size(); i++){a[i] = x[la - i - 1] - '0';}for (int i = 0; i < y.size(); i++){b[i] = y[lb - i - 1] - '0';}// 2、mul: a * b = cmul(a, b, c);// 3、输出结果for (int i = lc - 1; i >= 0; i--){cout << c[i];}return 0;
}
高精度除法
题目描述

题目解析
本题不是纯真的高精度除法,而是高精度除低精度。所以被除数需要用数组存储,除数用整型存储就行了。 思路还是模拟列竖式除法,需要用一个 long
long 类型的变量t来存储每次除后的余数。div步骤分三步走,因为被除数是逆序存储的,而除法需要从头开始,所以逆序遍历整个被除数数组:
1、求该次除的被除数:t = t * 10 + a[i]
2、除后结果为该位结果,c[i] = t / b
3、除后余数为新的t值, t %= b
本题还有两个注意事项:
1、处理前导0。
2、变量t要有long long存储,因为余数可能是1e9级别的,然后t*10就会超过int范围。
代码
#include <iostream>
#include <string>
using namespace std;typedef long long LL;
const int N = 1e5 + 10;
int a[N], c[N];
int la, lc;// 高精度除法模板(高精度 / 低精度)
void div(int a[], int b, int c[])
{LL t = 0; //存储除后的余数for (int i = la - 1; i >= 0; i--){t = t * 10 + a[i];c[i] = t / b;t %= b;}//处理前导0 while (lc > 1 && c[lc - 1] == 0){lc--;}
}int main()
{string x; //被除数int b; //除数cin >> x >> b;la = x.size();// 1、将被除数逆序存入数组for (int i = 0; i < x.size(); i++){a[i] = x[la - i - 1] - '0';}// 2、divlc = la;div(a, b, c);// 3、输出结果for (int i = lc - 1; i >= 0; i--){cout << c[i];}return 0;
}
以上就是小编分享的全部内容了,如果觉得不错还请留下免费的赞和收藏
如果有建议欢迎通过评论区或私信留言,感谢您的大力支持。
一键三连好运连连哦~~

