当前位置：首页 > news >正文

【AES加密】AES加密算法流程全解析

news 2025/10/31 4:29:14

零、相关内容

一、什么是加密?

1.加密算法的定义和基本概念

2.对称加密算法

原理:

常见算法:

3.非对称加密算法

原理:

常见算法:

二、AES

1.AES(advanced encryption standard 高级加密标准)介绍

2.对称加密算法与非对称加密算法的区别

3.AES的基本结构

4.加密流程

三、AES相关Q&A：

1.AES加密的信息长度是否有限制?是多长?

2.AES每次加密的信息最短不能短于多少?

3.什么是非对称加密?和对称加密的区别是什么?

4.非对称加密中公钥加密后的密文为什么无法用公钥解密？只有私钥才能解密？

1. 核心思想：单向函数与陷门

2. 一个简化的数学模型（基于RSA算法）

3. 一个绝佳的类比：信箱

5.对称加密与非对称加密的结合使用

零、相关内容

（这个视频做的非常好，非常推荐）

一、什么是加密?

1.加密算法的定义和基本概念

加密算法是一种数学函数,用于将原始信息(明文)转换为密文,使得未经授权的用户难以理解信息的内容。这个过程需要一个密钥,密钥是一个控制加密和解密过程的参数。加密算法主要分为对称加密算法和非对称加密算法。

2.对称加密算法

原理:

对称加密算法使用相同的密钥进行加密和解密。发送方和接收方必须共享这个密钥。例如,当用户A要发送一条消息给用户B时,他们需要事先协商好一个密钥。用户A使用这个密钥对消息进行加密,然后将密文发送给用户B。用户B收到密文后,使用相同的密钥进行解密,得到原始消息。

常见算法:

DES(数据加密标准):它是一种比较早期的对称加密算法。DES采用64位的分组长度,但是其中有效密钥长度为56位。由于密钥长度相对较短,现在已经不太安全,容易被暴力破解。例如,在早期的银行系统数据加密中曾经使用DES算法,但随着计算机计算能力的提升,其安全性受到挑战。

AES(高级加密标准):这是目前应用非常广泛的对称加密算法。AES支持128位、192位和256位的密钥长度。它的分组长度为128位。例如,在无线网络安全协议(如WPA2)、磁盘加密(如WindowsBitLocker)等众多领域都有应用。AES的安全性较高,在合理的时间内很难通过暴力破解获取密钥。

优点和缺点:
- 优点:加密和解密速度快,适用于大量数据的加密。因为使用相同的密钥,算法实现相对简单。
- 缺点:密钥管理困难。由于发送方和接收方需要共享密钥,在多个用户的网络环境中,密钥的分发和存储容易出现安全问题。如果密钥泄露,整个加密系统就会失效。

3.非对称加密算法

原理:

非对称加密算法使用一对密钥,即公钥和私钥。公钥可以公开,任何人都可以获取。私钥则由所有者保密。当用户A要发送消息给用户B时,用户A使用用户B公布的公钥对消息进行加密,然后发送给用户B。用户B收到密文后,使用自己的私钥进行解密。反过来,用户B也可以使用自己的私钥对消息签名,用户A可以使用用户B的公钥验证签名的真实性。

常见算法:

RSA:这是最著名的非对称加密算法之一。
ECC(椭圆曲线密码学):ECC是基于椭圆曲线离散对数问题的非对称加密算法。

优点和缺点:

优点:密钥管理方便,公钥可以公开分发,不需要像对称加密那样担心密钥的安全分发问题。并且可以用于数字签名,确保消息的来源和完整性。
缺点:加密和解密速度相对较慢,尤其是对于较长的消息或大量数据,计算成本较高。

二、AES

1.AES(advanced encryption standard 高级加密标准)介绍

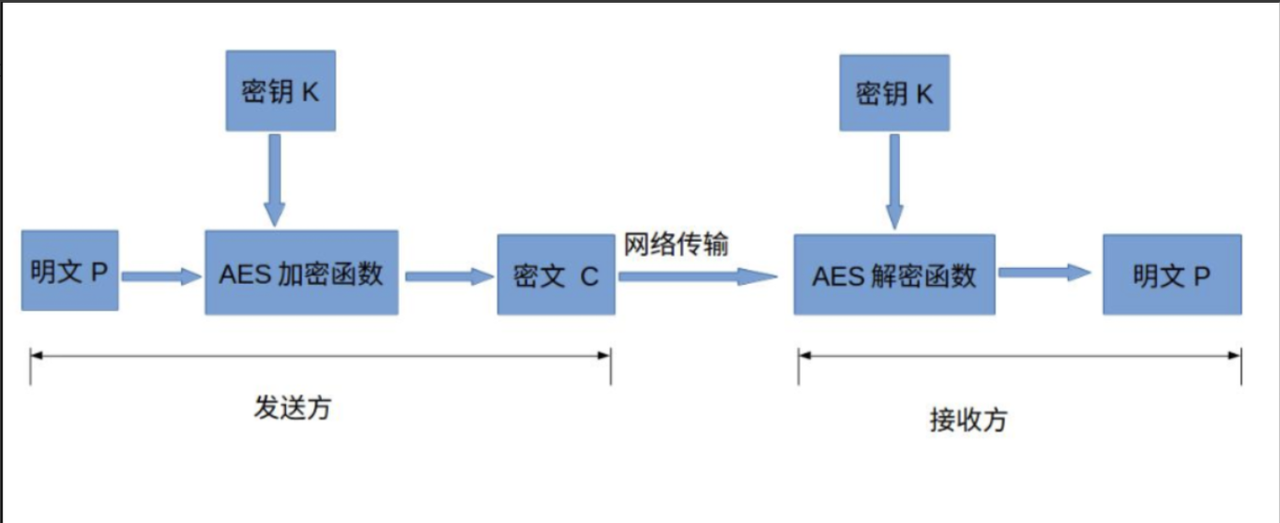
明文P
- 没有经过加密的数据。
秘钥K
- 用来加密明文的密码,在对称加密算法中,加密与解密的密钥是相同的。密钥为接收方与发送方协商产生,但不可以直接在网络上传输,否则会导致密钥泄漏,通常是通过非对称加密算法加密密钥,然后再通过网络传输给对方,或者直接面对面商量密钥。密钥是绝对不可以泄漏的,否则会被攻击者还原密文,窃取机密数据。
AES加密函数
- 设AES加密函数为E,则C=E(K,P),其中P为明文,K为密钥,C为密文。也就是说,把明文P和密钥K作为加密函数的参数输入,则加密函数E会输出密文C。
密文C
- 经加密函数处理后的数据
AES解密函数
- 设AES解密函数为D,则P=D(K,C),其中C为密文,K为密钥,P为明文。也就是说,把密文C和密钥K作为解密函数的参数输入,则解密函数会输出明文P。

2.对称加密算法与非对称加密算法的区别

对称加密算法
- 加密和解密用到的密钥是相同的,这种加密方式加密速度非常快,适合经常发送数据的场合。缺点是密钥的传输比较麻烦：我加密了一段信息，我想要你解密这段信息，我就必须把密钥发送给你，如果密钥在发送过程中被截获破解，密文也就变成了明文。
非对称加密算法
- 加密和解密用的密钥是不同的,这种加密方式是用数学上的难解问题构造的,通常加密解密的速度比较慢,适合偶尔发送数据的场合。优点是密钥传输方便：我无需向你传输密钥，也不需要知道私钥的内容，由于公钥加密的单向性（即无法直接通过公钥破解密文），在加密传输中，我将明文通过公钥加密，你接收到密文后使用私钥解密得到明文，私钥不会传递，自然安全。
- 常见的非对称加密算法为RSA、ECC和EIGamal。

3.AES的基本结构

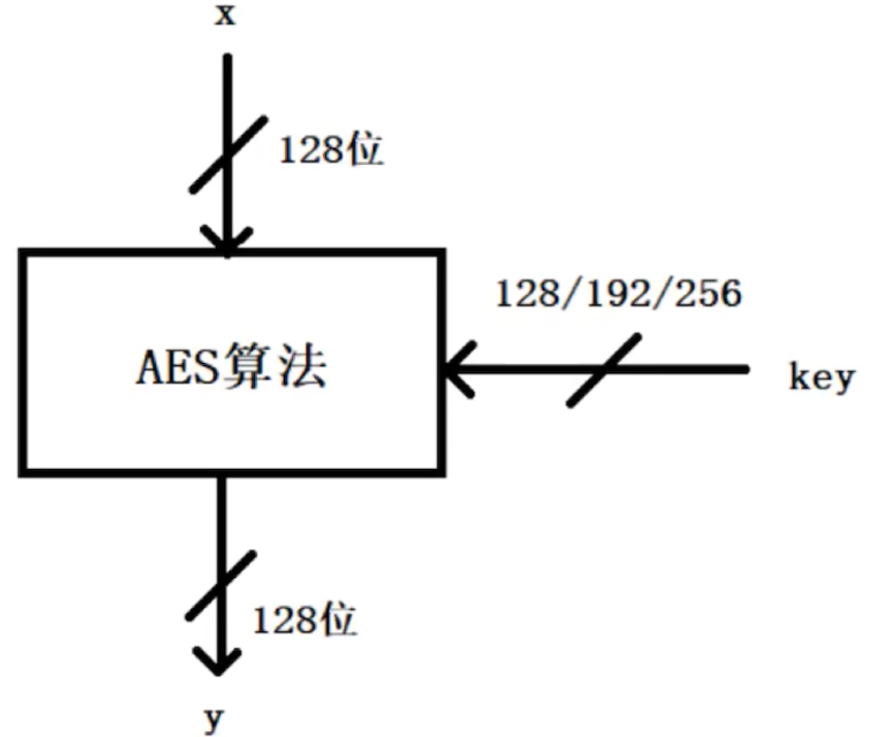
AES的基本结构是一个分组加密的框架,通常分为若干“轮”(round)来处理数据。AES的加密过程由初始轮、多个主轮和最后一个轮组成,每一轮执行特定的数据处理步骤,确保密文的安全性和混淆性。

在AES标准规范中,分组长度只能是128位,也就是说,每个分组为16个字节(每个字节8位)。密钥的长度可以使用128位、192位或256位。密钥的长度不同,推荐加密轮数也不同,如下表所示:

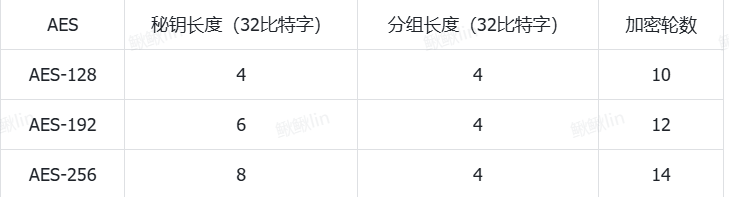
密钥长度是指在加密算法中使用的密钥的位数或字节数。它是加密强度的重要因素,通常以比(bit)为单位表示。密钥长度直接影响到加密算法的安全性和计算复杂度。

分组长度是指分组加密算法在处理数据时,每次处理的固定长度数据块的大小,通常以字节(Bytes)或比特(Bits)为单位。

加密轮数(Number of Rounds)指的是对每个数据分组执行加密处理的重复次数。每一轮加密都是对数据进行一系列特定的操作,包括字节替换(SubBytes)、行移位(ShiftRows)、列混淆(MixColumns),以及与密钥的轮密钥加(AddRoundKey)运算。轮数的增加使得AES更具抗攻击性。

4.加密流程

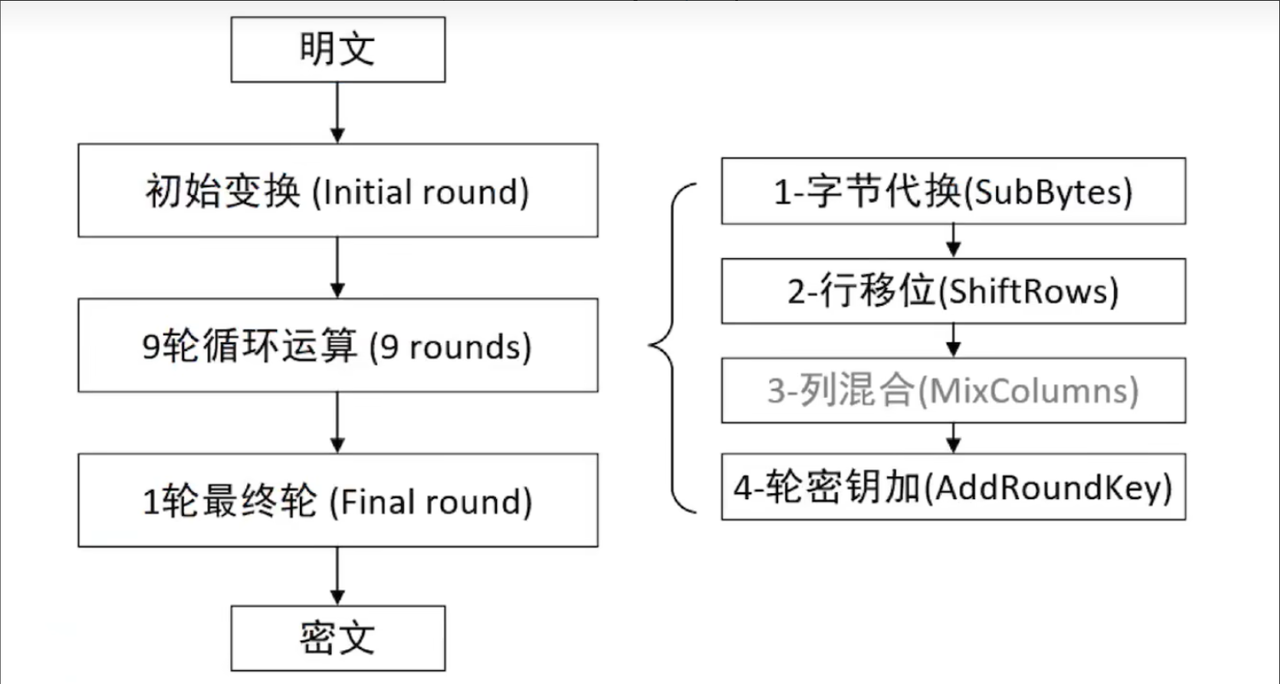
a. 密钥扩展(Key Expansion)

将输入的密钥通过一个密钥扩展算法,生成多个轮密钥(Round Keys)。
AES-128 会生成11个轮密钥(原密钥+10轮加密密钥)。

b. 初始轮操作(Initial Round)

AddRoundKey:将明文和第一个轮密钥进行按位异或(XOR)操作。

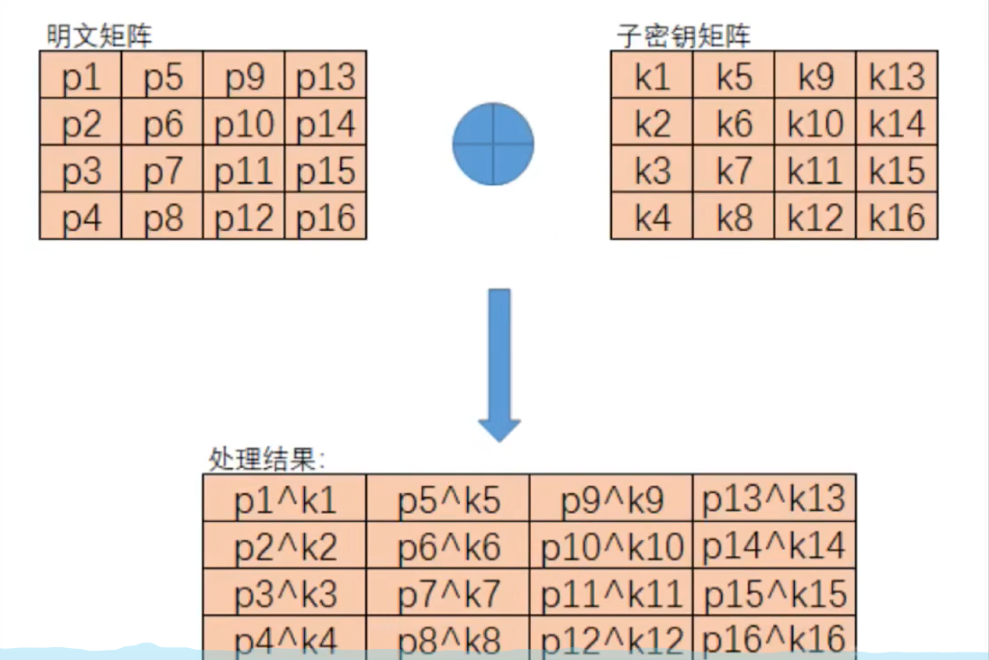
c. 主要轮操作(Main Rounds)

每一轮包括以下四个步骤:

使用S-Box(置换盒)对每个字节进行非线性替换,提高算法的安全性。
- SubBytes(字节替换)

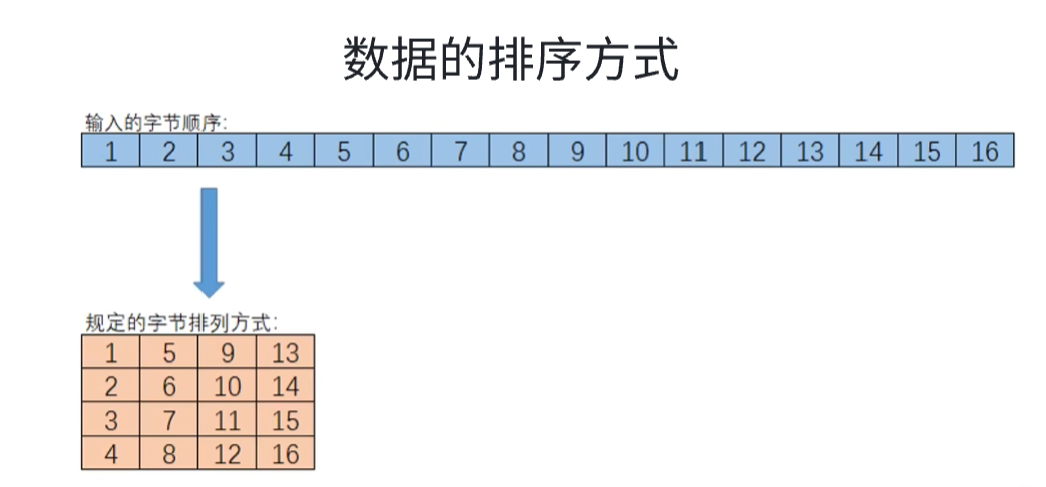
ShiftRows(行移位)

对状态矩阵的每一行按固定规则进行循环左移。

MixColumns(列混合)

对状态矩阵的每一列进行线性变换,增强列间的混淆性。

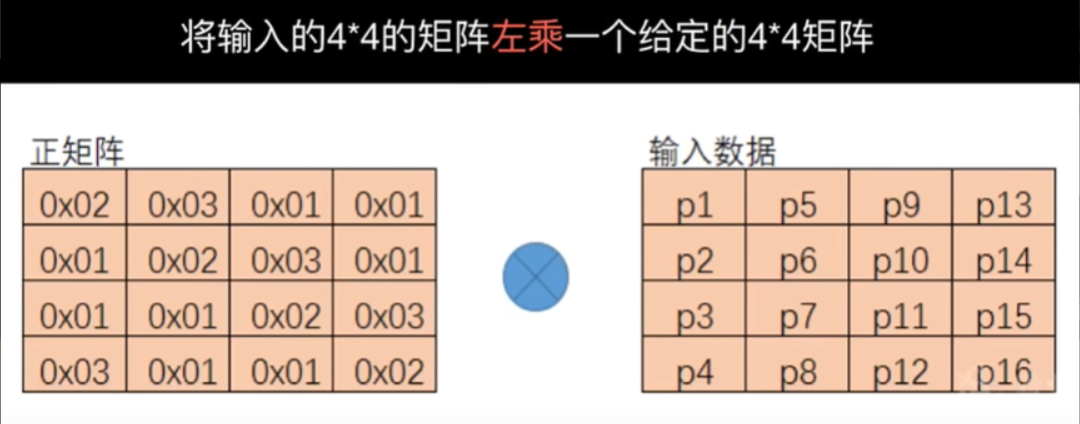
AddRoundKey(轮密钥加)

将状态矩阵与当前轮的轮密钥按位异或(XOR)。

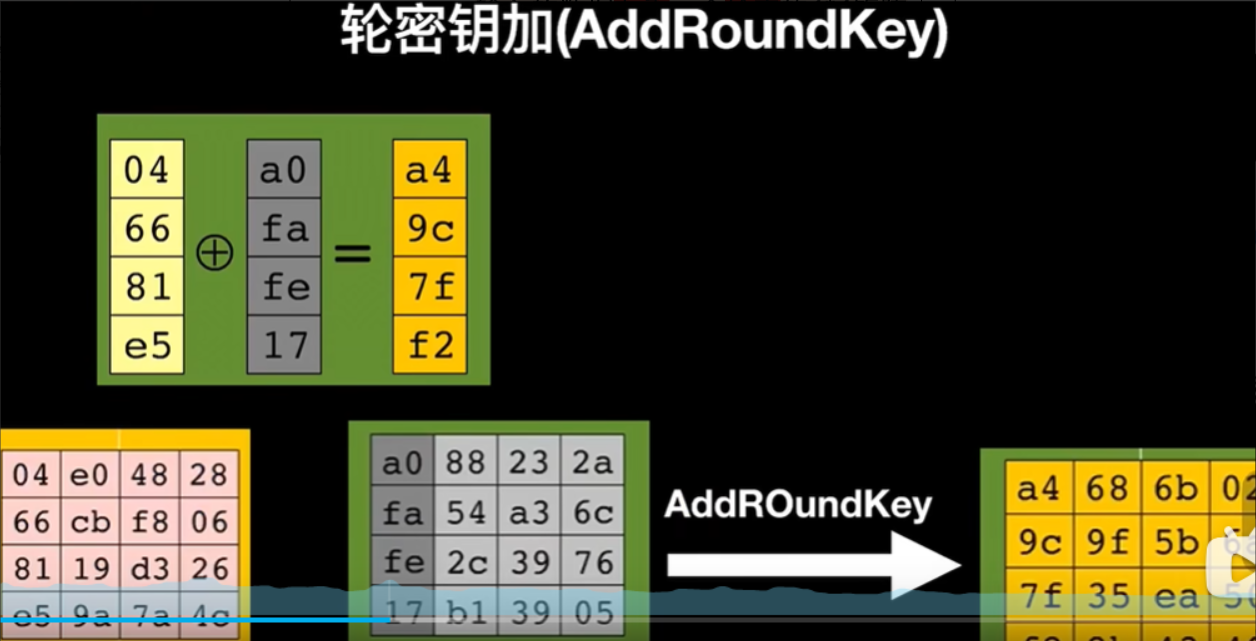
d. 最终轮操作(Final Round)

和主要轮类似,但省略MixColumns（列混合）步骤。

三、AES相关Q&A：

1.AES加密的信息长度是否有限制?是多长?

AES本身没有限制加密数据的长度,但要注意的是,AES加密是以块为单位处理数据的,每个块通常是128位(16字节)。对于超过一个块的数据,需要使用某种模式来链接多个块,如CBC(Cipher Block Chaining)、CFB(Cipher Feedback)、OFB(Output Feedback)等。

2.AES每次加密的信息最短不能短于多少?

AES加密的最小单位是一个块,即128位(16字节)。如果加密的数据少于这个长度,通常会用填充

(Padding)技术将其扩展到一个完整的块大小。

3.什么是非对称加密?和对称加密的区别是什么?

非对称加密使用一对密钥,一个是公开的公钥,另一个是私有的私钥。发送者使用接收者的公钥加密消息,而接收者使用其私钥解密。比如RSA创建的ssh密钥对进行加密解密

对称加密则使用相同的密钥进行加密和解密。比如AES加密解密

4.非对称加密中公钥加密后的密文为什么无法用公钥解密？只有私钥才能解密？

简单直接的答案是：因为公钥和私钥在数学上是严格绑定的，但它们的角色被设计成单向的。加密和解密使用的是两种完全不同的数学运算，而公钥并不具备反向运算的能力。

下面我们从几个层面来深入解释：

1. 核心思想：单向函数与陷门

非对称加密基于一种叫做“单向函数”的数学概念。

单向函数：正向计算很容易，但反向计算极其困难。
一个生活化的比喻：混色。将黄色和蓝色两种颜料混合，得到绿色，这非常容易（正向计算）。但给你一罐绿色颜料，让你分离出原始的黄色和蓝色颜料，这几乎是不可能的（反向计算）。

非对称加密算法就是找到了一种特殊的单向函数，它带有一个“陷门”。这个陷门信息就是私钥。

没有陷门：给你密文和公钥，你无法反向计算出明文（就像无法分离颜料）。
有陷门（私钥）：你可以轻松地反向计算，解出明文。

2. 一个简化的数学模型（基于RSA算法）

我们以最经典的RSA算法为例，用一个极度简化的数字来说明其思想（实际使用的数字巨大无比）。

密钥生成阶段：

选择两个质数：p = 3, q = 11。
计算它们的乘积：n = p * q = 33。这个n会成为公钥和私钥的一部分。
计算欧拉函数：φ(n) = (p-1)*(q-1) = 2 * 10 = 20。
选择一个公钥指数 e，条件是 1 < e < φ(n)，且 e 与 φ(n) 互质。我们选 e = 3。
1. 此时，公钥 = (e, n) = (3, 33)。
计算私钥指数 d，条件是 (d * e) % φ(n) = 1。经过计算，d = 7，因为 (7 * 3) % 20 = 21 % 20 = 1。
1. 此时，私钥 = (d, n) = (7, 33)。

加密与解密过程：

假设我们要加密一个秘密数字 M = 4。

加密（用公钥）：

密文 C = M^e % n = 4³ % 33 = 64 % 33 = 31。

我们把密文 31 发送出去。

解密（用私钥）：

明文 M‘ = C^d % n = 31⁷ % 33。

31⁷ 是一个很大的数（27,512,614,111），但我们只关心它除以33的余数。通过数学计算可以得出，余数正好是 4。

M’ = 4，成功解密！

为什么不能用公钥(3, 33)解密？

如果你想用公钥 (3, 33) 去解密密文 31，你需要解下面这个方程：

X³ % 33 = 31

在不知道 p、q、φ(n) 和 d 的情况下，求解 X 就是一个典型的“离散对数问题”，对于小数字你可以暴力破解，但当 n 是一个长达数百位甚至上千位的天文数字时，即使用世界上最快的计算机，也需要花费数百万年才能算出来。这就是数学上的计算复杂性保证了安全性。

总结一下关键点：

数学绑定，功能分离：公钥和私钥源于同一组数学参数，但被设计用于不同的数学运算。加密用 e 次方，解密必须用 d 次方。这两个操作是不可互换的。
安全基于数学难题：非对称加密的安全性依赖于大数分解难题（RSA）或离散对数问题等，这些问题在可预见的时间内是无法被经典计算机解决的。
公钥是公开的“锁”：你可以把公钥想象成一把任何人都能拿到的打开的挂锁。任何人都可以用它来锁上盒子（加密），但一旦锁上，只有拥有唯一钥匙（私钥）的人才能打开（解密）。