当前位置：首页 > news >正文

C++ stack和queue之OJ题目

news 2025/10/31 4:25:56

题目一、最小栈

设计一个支持 push，pop，top操作，并能在常数时间内检索到最小元素的栈。
实现 MinStack 类 :
MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素，时间复杂度位O（1）

思路：用两个栈，然后用其中一个栈存储数据，另一个栈存储每次往里push数据时，当前的最小数，也就是对应那个栈的最小元素

class MinStack 
{
public:MinStack() //这里不初始化也没问题，因为自定义类型会去调用它自己的默认构造{}void push(int val) {_st.push(val);//_minst插入数据的两种情况：为空或者val小于等于_minst的栈顶元素if (_minst.empty() || val <= _minst.top()){_minst.push(val);}}void pop() {//pop之前先判断_st是否和_minst相等，不相等直接pop，相等两个一起popif (_st.top() == _minst.top()){_minst.pop();}_st.pop();}int top() {return _st.top();}int getMin() //获取栈里面的最小元素{return _minst.top();}
private:stack<int> _st;stack<int> _minst;
};

题目二、栈的弹出、压入序列

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。
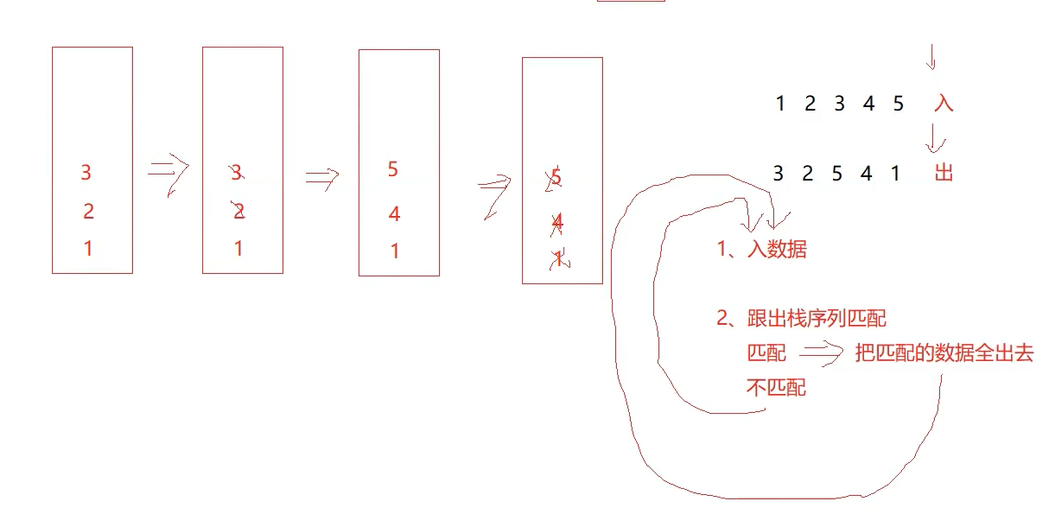
假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序
列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。
1. 0 <= pushV.length == popV.length <= 1000
2. -1000 <= pushV[i] <= 1000
3. pushV 的所有数字均不相同

思路：模拟其如数据和出数据，每入一个就和这个出来的序列匹配，匹配上了就出，然后继续匹配，不匹配就继续入栈

class Solution {
public:bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {stack<int> st;int pushi = 0;int popi = 0;while (pushi < pushV.size()){//依次入栈st.push(pushV[pushi++]);//判断栈顶是否和popV相等if (st.top() != popV[popi]){//不相等就继续入数据continue;}else{//如果两个相等while (!st.empty() && st.top() == popV[popi]){//出栈st.pop();++popi;}}}return st.empty();}
};

这个代码还可以进行以下优化：（因为本质都要一直持续入，只要匹配就出）

class Solution {
public:bool IsPopOrder(vector<int>& pushV, vector<int>& popV){stack<int> st;int pushi = 0;int popi = 0;while (pushi < pushV.size()){//依次入栈st.push(pushV[pushi++]);//判断栈顶是否和popV相等//如果两个相等while (!st.empty() && st.top() == popV[popi]){//出栈st.pop();++popi;}}return st.empty();}
};

题目三、逆波兰表达式求值

给你一个字符串数组tokens,表示一个根据逆波兰表示法表示的算术表达式，请你计算该表达式，返回一个表示表达式值的整数。
注意：
有效的算符为 '+'、'-'、'*' 和 '/'
每个操作数（运算对象）都可以是一个整数或者另一个表达式
两个整数之间的除法总是向零截断
表达式中不含除零运算
输入是一个根据逆波兰表示法表示的算术表达式
答案及所有中间计算结果可以用 32 位整数表示

例如；
2 + 1 * 3 中缀表达式
2 1 3 * + 后缀表达式（操作数的顺序不变，操作符按优先级重排）

获得后缀表达式的方法：操作数输出，而操作符（如果栈为空，且当前操作符的优先级比栈顶的高，继续入栈，如果栈不为空，且当前操作符比栈顶的优先级低或者相等，则输出栈顶的操作符），表达式结束后，依次出栈里面的操作符

思路：在对后缀表达式进行计算，对得到的进行入栈，遇到操作符就把栈顶的两个元素拿出来进行操作符计算

class Solution 
{
public:int evalRPN(vector<string>& tokens) {stack<int> st;for (auto& element : tokens){if (element == "+" || element == "-" || element == "*" || element == "/"){//遇到操作符就取出栈顶元素进行计算int num1 = st.top();st.pop();int num2 = st.top();st.pop();//判断运算符是什么，然后对num1和num2进行运算符操作switch (element[0]){case '+':st.push(num2 + num1);break;case '-':st.push(num2 - num1);break;case '*':st.push(num2 * num1);break;case '/':st.push(num2 / num1);break;}}else {//是数字就入栈st.push(stoi(element));}}//返回最后计算所得栈顶元素return st.top();}
};

练习四、用两个栈实现队列

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：
实现 MyQueue 类：
void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空，返回 true ；否则，返回 false

思路：用两个栈，一个栈入数据，另一个栈出数据

class MyQueue 
{
public:MyQueue() {//调用stack自定义类型自己的构造函数}void push(int x) {//把元素先放到inst里面，在放到outst里面去inst.push(x);}int pop() {//判断outst是否为空if (!outst.empty()){int num = outst.top();outst.pop();return num;}else if (outst.empty() && inst.empty()){return false;}else{//把inst所有的元素全部移到outst里面，在出while (!inst.empty()){int num1 = inst.top();inst.pop();outst.push(num1);}int num2 = outst.top();outst.pop();return num2;}}int peek() {//判断outst是否为空if (!outst.empty()){int num = outst.top();return num;}else if (outst.empty() && inst.empty()){return false;}else{//把inst所有的元素全部移到outst里面，在出while (!inst.empty()){int num1 = inst.top();inst.pop();outst.push(num1);}int num2 = outst.top();return num2;}}bool empty() {return inst.empty() && outst.empty();}
private:stack<int> inst;stack<int> outst;
};

练习五、二叉树的层序遍历

给你二叉树的根节点root，返回其节点值的层序遍历（即逐层地，从左到右访问所有节点）

思路：使用队列对二叉树进行层序遍历
1.使用双队列，一个队列表示节点内容，另一个队列表示这个节点的层次
2.一个变量控制每一层的个数（levelsize），一层一层出

struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode() :val(0),left(nullptr),right(nullptr) {}TreeNode(int x) :val(x),left(nullptr),right(nullptr) {}TreeNode(int x, TreeNode* left, TreeNode* right) :val(x),left(left),right(right) {}
};
class Solution 
{
public:vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> vv;queue<TreeNode*> q;size_t levelsize = 0;if (root != NULL){//把根节点放进队列q中q.push(root);levelsize = 1;}while (!q.empty()){vector<int> v;//一层一层出数据for (size_t i = 0; i < levelsize; ++i){//出头数据v.push_back(q.front()->val);//保存当前节点TreeNode* front = q.front();q.pop();//在入数据if (front->left != NULL){q.push(front->left);}if (front->right != NULL){q.push(front->right);}}//重置levelsizelevelsize = q.size();//把一层的数据中全部放进vvvv.push_back(v);}return vv;}
};

练习六、自底向上层序遍历

给你二叉树的根节点 root ，返回其节点值自底向上的层序遍历（即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

思路：直接撑场层序遍历，然后直接对二维数组进行逆置

struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode():val(0), left(nullptr), right(nullptr){}TreeNode(int x):val(x), left(nullptr), right(nullptr){}TreeNode(int x, TreeNode* left, TreeNode* right):val(x), left(left), right(right){}
};
class Solution
{
public:vector<vector<int>> levelOrderBottom(TreeNode* root){vector<vector<int>> vv;queue<TreeNode*> q;size_t levelsize = 0;if (root != NULL){//把根节点放进队列q中q.push(root);levelsize = 1;}while (!q.empty()){vector<int> v;//一层一层出数据for (size_t i = 0; i < levelsize; ++i){//出头数据v.push_back(q.front()->val);//保存当前节点TreeNode* front = q.front();q.pop();//在入数据if (front->left != NULL){q.push(front->left);}if (front->right != NULL){q.push(front->right);}}//重置levelsizelevelsize = q.size();//把一层的数据中全部放进vvvv.push_back(v);}reverse(vv.begin(), vv.end());return vv;}
};

查看全文

http://www.dtcms.com/a/539960.html