长春网站建设公司seo是什么意思教程

目录

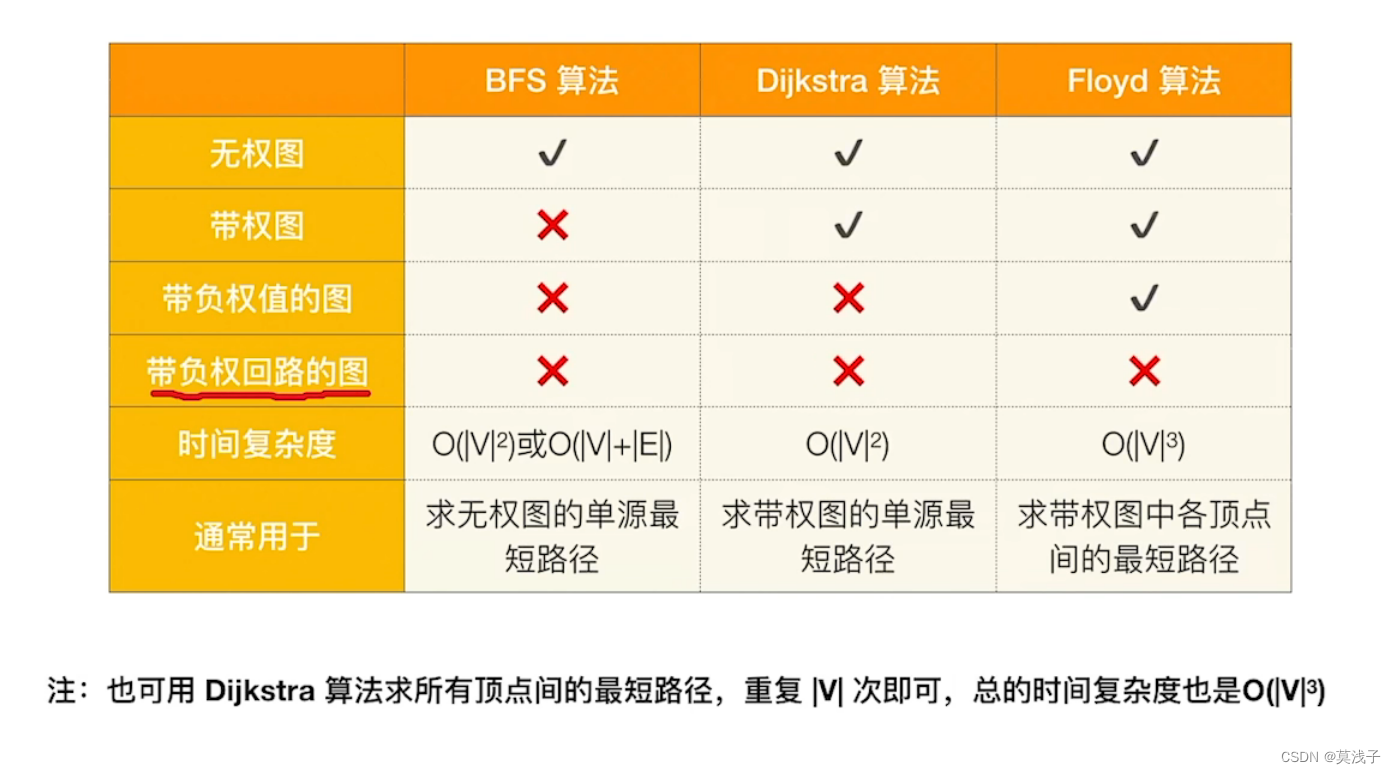
1.BFS算法

2.Dijkstra算法

3.Floyd算法

4.总结

---

1.BFS算法

G纲是个物流离散中心，经常需要往各个城市运东西，怎么运送距离最近——单源最短路径问题

各个城市之间也学要来往，相互之间怎么走距离最近？——每对顶点之间的最短路径

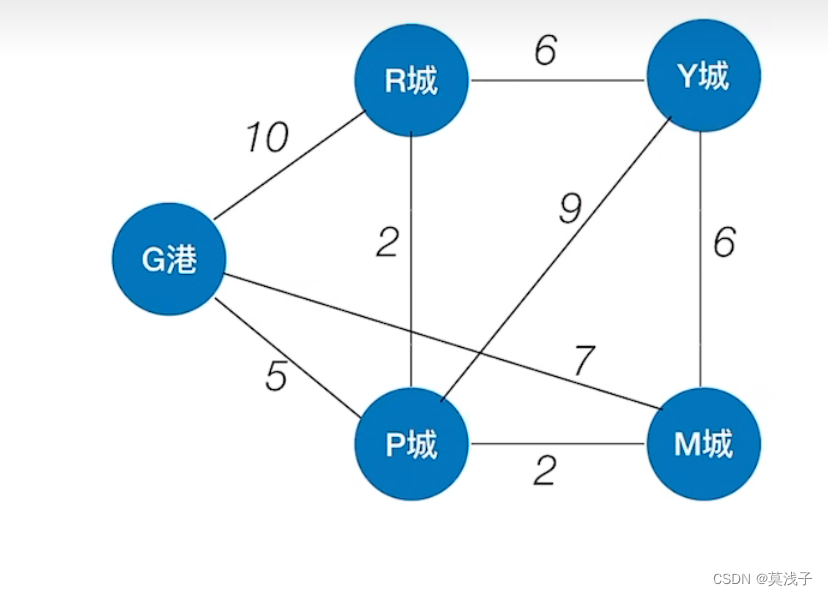
如下图,BFS算法是如何实现最短路径问题的呢？设从顶点2开始，第一次搜索的结点为1号结点和6号结点，路径为1，从1号结点和6号结点开始找相邻的接地，5号结点和3号7号为相邻的结点，然后5号结点周围都是已经访问过的，3号结点和7号结点分别搜索搭配4号和8号结点，路径为4 

代码 

void BFS_MIN_Distance(Graph G,int u){//d[i]表示从u到i结点的最短路径for(int i = 0;i <G.vexnum;i ++){d[i] = -1 ;        //初始化路径长度path[i] = -1;     //最短路径从哪个顶点过来 } d[u] = 0;visited[u] = TRUE;EnQueue(Q,u);while(!isEmpty(Q)) {             //BFS算法过程 DeQueue(Q,u);               //对头元素u出队for(w = FirstNeighbor(G,u); w >=0 ;w = NextNeighbor(G,u,w))if(!visited[w]){d[w] = d[u] + 1;    // w为u的尚未访问的领结点 path[w] = u;        //最短路径应从u到w visited[w] = u;     // 设已访问标记 EnQueue(Q,w);       //顶点w入队 } }
} 

2.Dijkstra算法

BFS算法的局限性

BFS算法只适用于求无权图，或所有边的权值都相同的图。

迪杰斯特拉最短路径算法可以解决

final：标记是否找到最短路径

dist：最短路径长度

path：路径上的前驱

首先v1和v4距离v0的路径长度分别为10和5，v0到本身的距离就位0

首先遍历所有没确定最短路径的点，v0是0，确定了，在v1,v2,v3,v4中找最短的是v4的5，

然后从经过v4开始 到v1的最短路径变为8，到v2的最短路径变为14，到v3的最短路径值改为7.

同时修改path的值。

第二轮循环中，如果遍历发现最小的v3，把v3final值设为true。然后看其他没有确定的点，经过v3到v2的最短路径为7+6= 13，修改dist[2]的值为13，在修改其path的值。

第三次循环 在v1和v2中，发现v1的dist值最少，将v1的final值改为true，经过v1的v2最短路径长度为9，修改为9，同时修改path的值。 

第四次循环遍历所有结点，发现未遍历的最小的为v2，然后就找不到了 。

通过path【】可知，v0到v2的最短带权路径v2<--v1<--v4<--v0。

时间复杂度

带负权值的图

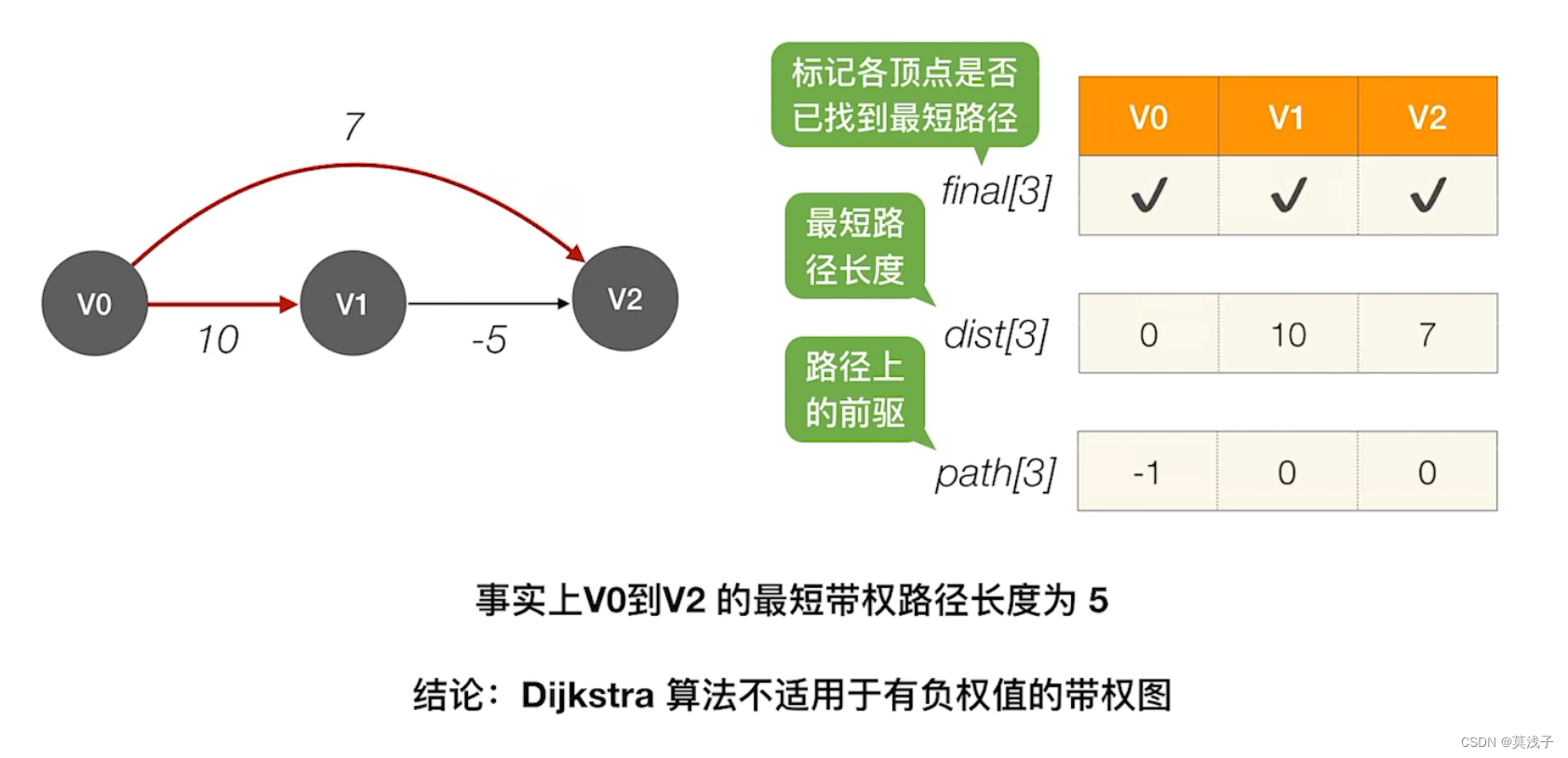
3.Floyd算法

Floyd算法:求出每一对顶点之间的最短路径

使用动态规划思想，将问题的求解分为多个阶段
对于n个顶点的图G，求任意一对顶点Vi->Vj之间的最短路径可分为如下几个阶段:#初始:不允许在其他顶点中转，最短路径是?

#0:若允许在Vo中转，最短路径是?
#1∶若允许在Vo、V中转,最短路径是?#2:若允许在Vo、V1、V2中转，最短路径是?...
#n-1:若允许在Vo、V1、V2.......Vn-1中转，最短路径是?

算法实现

1. 

2.

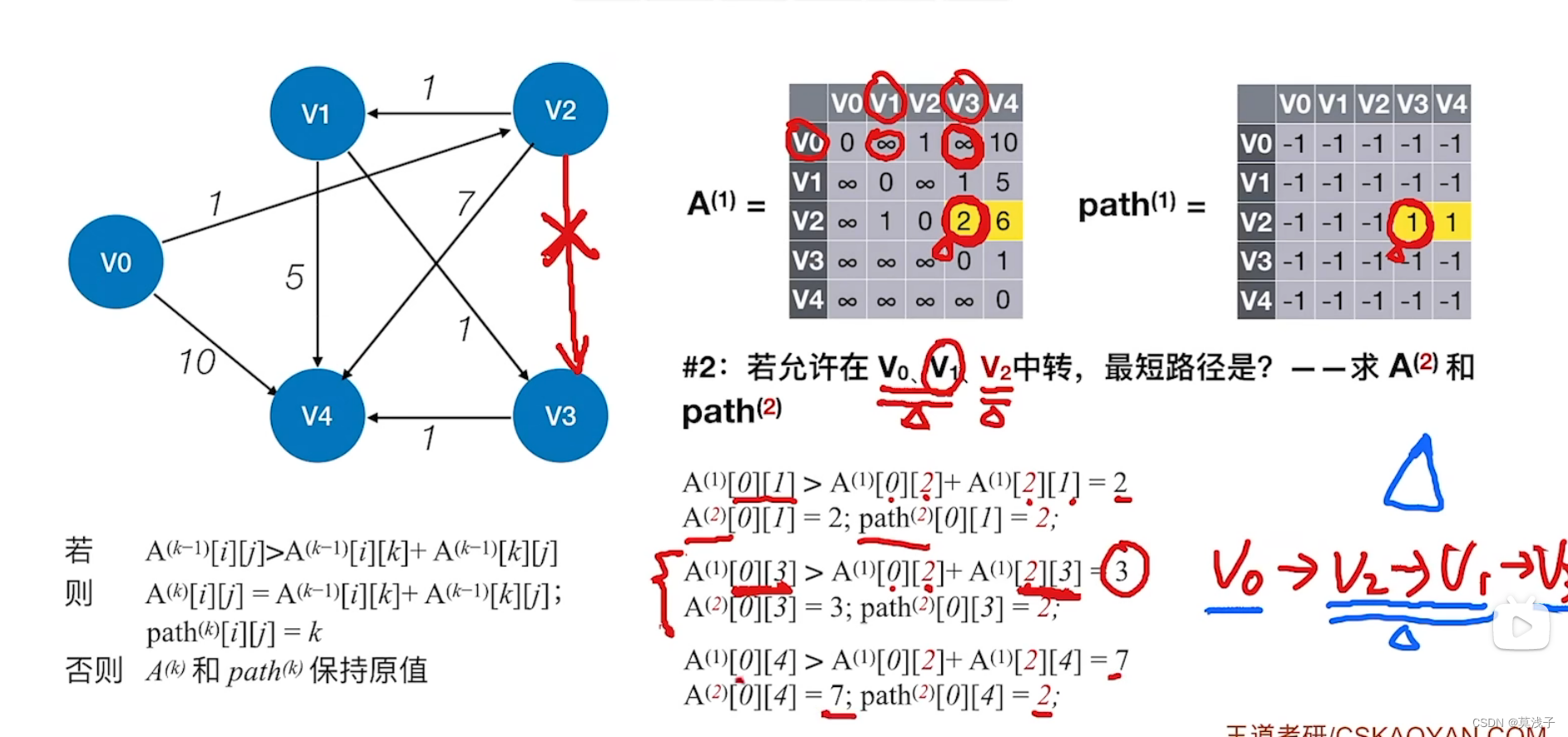
3.

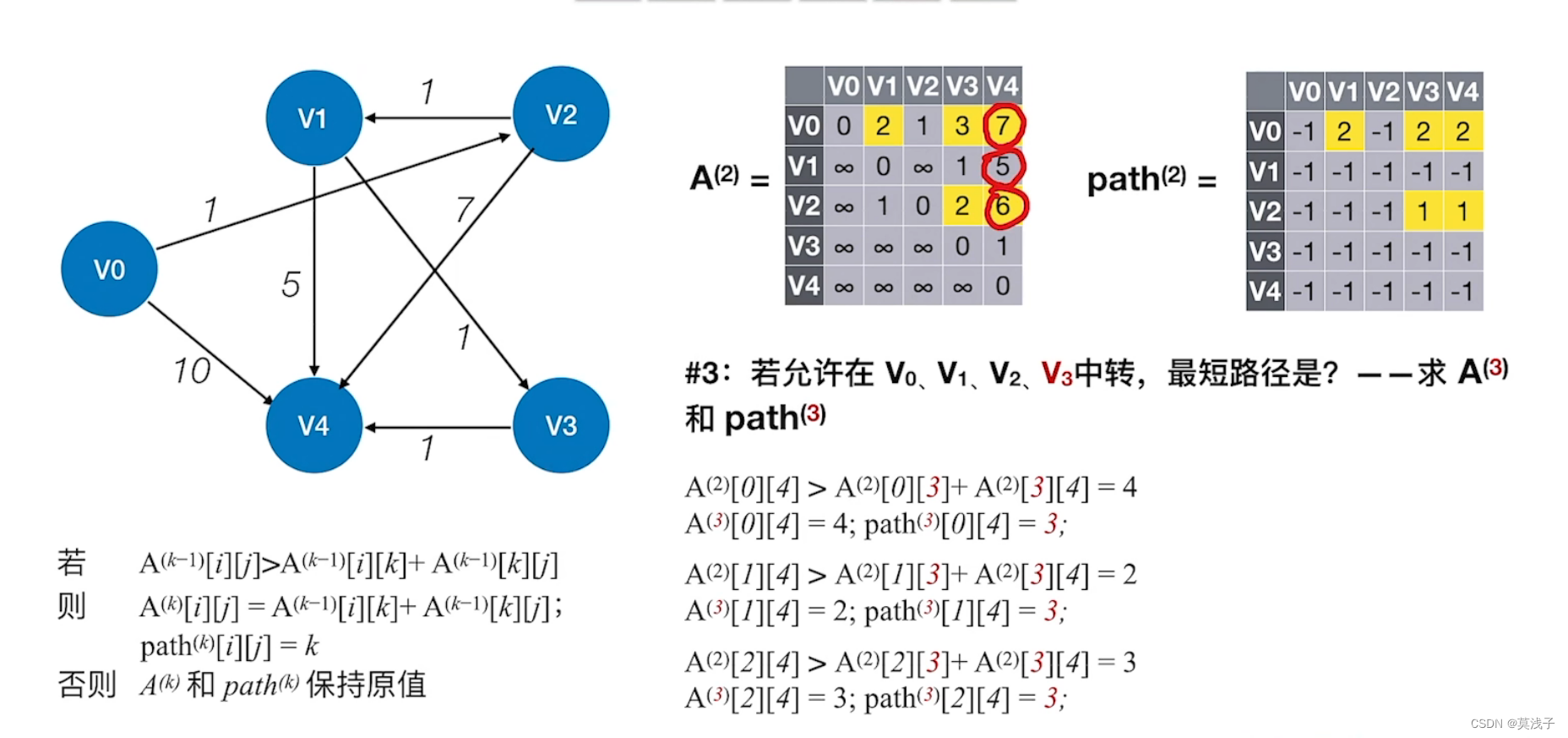
 经过v4的时候发现任何一个代码都不需要修改。

代码实现如下

l l ... ...准备工作，根据图的信息初始化矩阵A和 path (如上图)
for (int k=0 ; k<n ; k++){          //考虑以Vk 作为中转点for(int i=0; i<n; i++) {           //遍历整个矩阵，i为行号，j为列号for (int j=0; j<n; j++){if (A[i][j]>A[i] [k]+A[k][j]){   //以vk为中转点的路径更短A[i][j]=A[ i] [k ]+A[k][j];  //更新最短路径长度path[ i][j]=k;    //中转点       }}}}

那么假如实现完成如何去找一个完整的路径呢

首先 v0 到 v4 通过 path[0][4]可知为3，所以

v0       v3        v4

然后v3到v4是没有中转点的，在再看v0和v3也就是path[0][3] 有2 这个中转点，所以填为

v0    v2   v3       v4

最后再找，只有v2 和v3之间有个中转点，中转点为v1

所以

v0   v2  v3  v1    v4  

最后Floyd算法可以实现负权图，不能实现带负权值的组成的回路

4.总结