【编译原理笔记】3.4 Tokens Recognization

1、Finite State Automata（有限状态自动机）

1.1 非确定性有限自动机（NFA）

定义组成：

1. 状态集合S：有限的状态集

2. 输入字母表Σ：不包括空字符串ε

3. 转移函数：对于每个状态和Σ∪{ε}中的符号，给出下一状态集合

4. 起始状态s₀：特殊的开始状态

5. 接受状态集合F：S的子集

关键特性：

• 允许ε转移（空转移）

• 同一输入可能转移到多个状态

• 接受条件：存在一条从起始状态到接受状态的路径，路径上的符号序列构成输入字符串

1.2 确定性有限自动机（DFA）

定义组成：

• 与NFA类似，但转移函数是确定性的

• 对每个状态和Σ中的符号，有唯一的下一状态

• 不允许ε转移

---

2、RE、NFA、DFA之间的等价转换

我们以以下例题来具体介绍：

Please construct a DFA with minimum states for the following regular expression.

2.1 RE to NFA（从正则表达式到NFA的转换）

2.1.1 Thompson构造算法

输入：正则表达式r over Σ 输出：接受L(r)的NFA

基础情况：

1. 对于ε：创建两个状态，通过ε连接

2. 对于a∈Σ：创建两个状态，通过a连接

归纳构造：

1. 选择运算(r|s)：并行连接两个NFA

2. 连接运算(rs)：串联连接两个NFA

3. 闭包运算(r*)：添加ε转移实现循环

2.1.2 例题解答

题中给出的是RE（正则表达式），第一步先将RE转换为NFA：

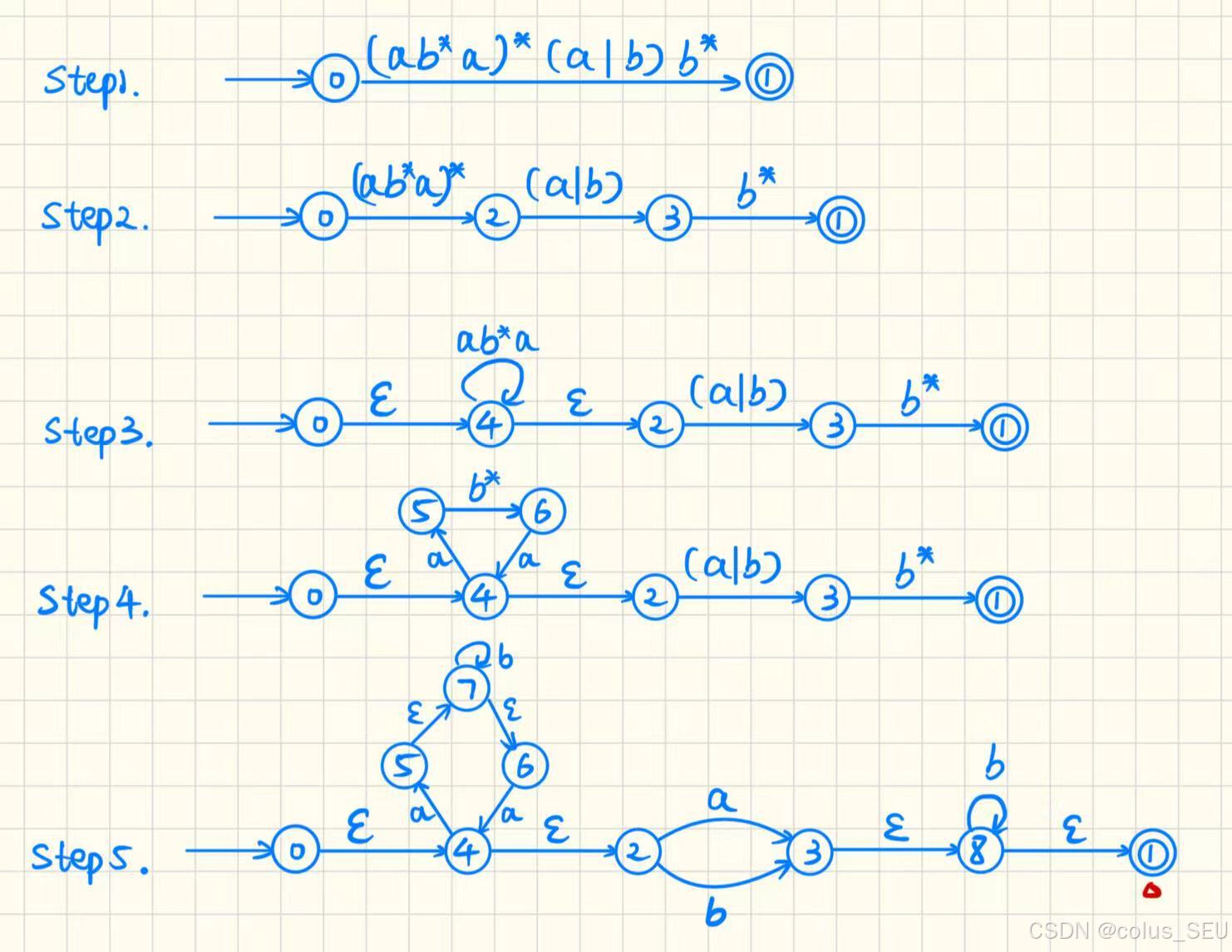
核心原则——将多步变为单步，遵循以下变换规则:

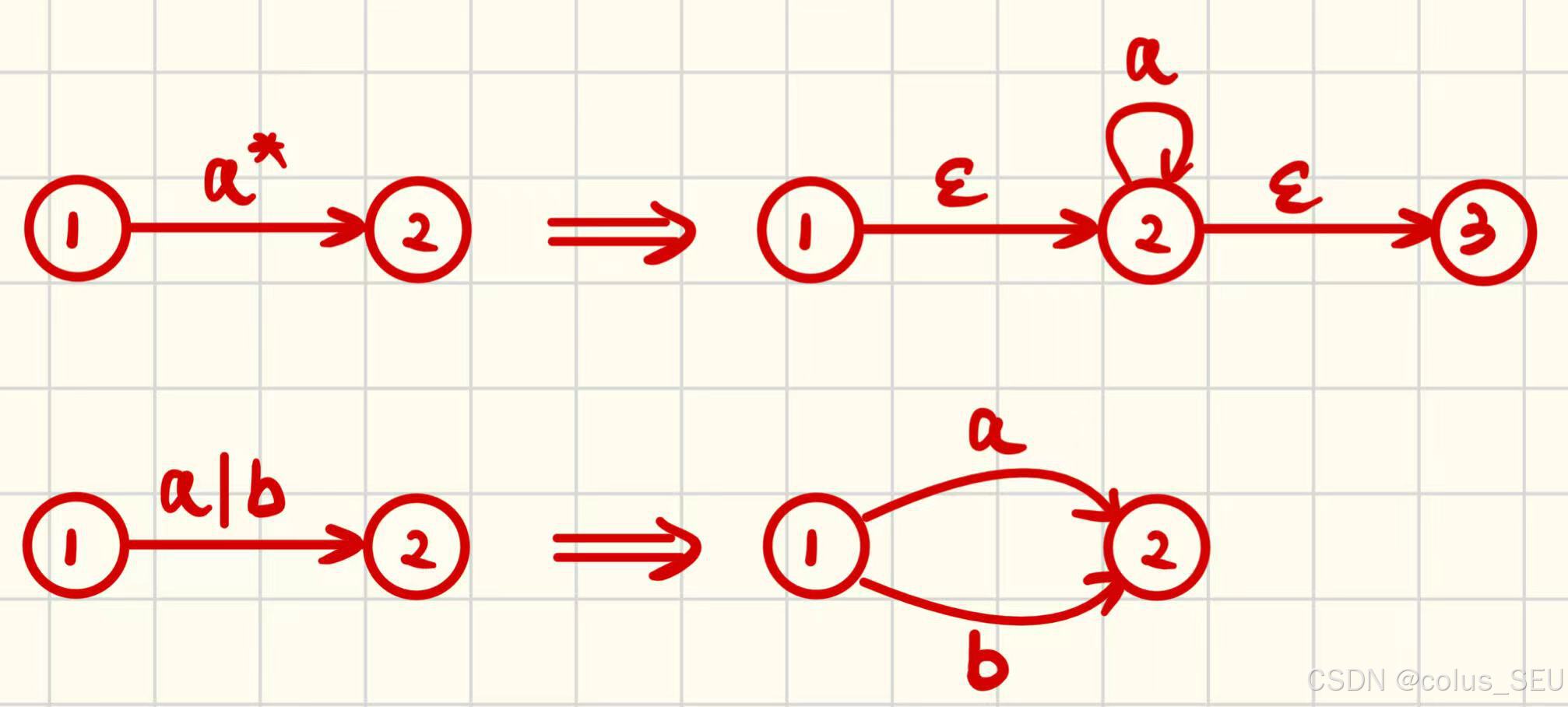
2.2 NFA to DFA

2.2.1 核心概念

• ε-闭包：从给定状态通过ε转移可达的所有状态集合

• move函数：从状态集合在输入符号a下的转移结果

子集构造算法

 初始化Dstates包含ε-closure(s₀)while (Dstates中有未标记状态T) {标记Tfor (每个输入符号a) {U = ε-closure(move(T, a))if (U不在Dstates中)添加U为未标记状态Dtran[T, a] = U}}

ε-闭包计算

 function ε-closure(T) {push all states in T onto stackresult = Twhile (stack not empty) {pop t from stackfor (每个状态u，满足t→u通过ε转移) {if (u不在result中) {add u to resultpush u onto stack}}}return result}

2.2.2 例题解答

第二步将NFA转换为DFA：

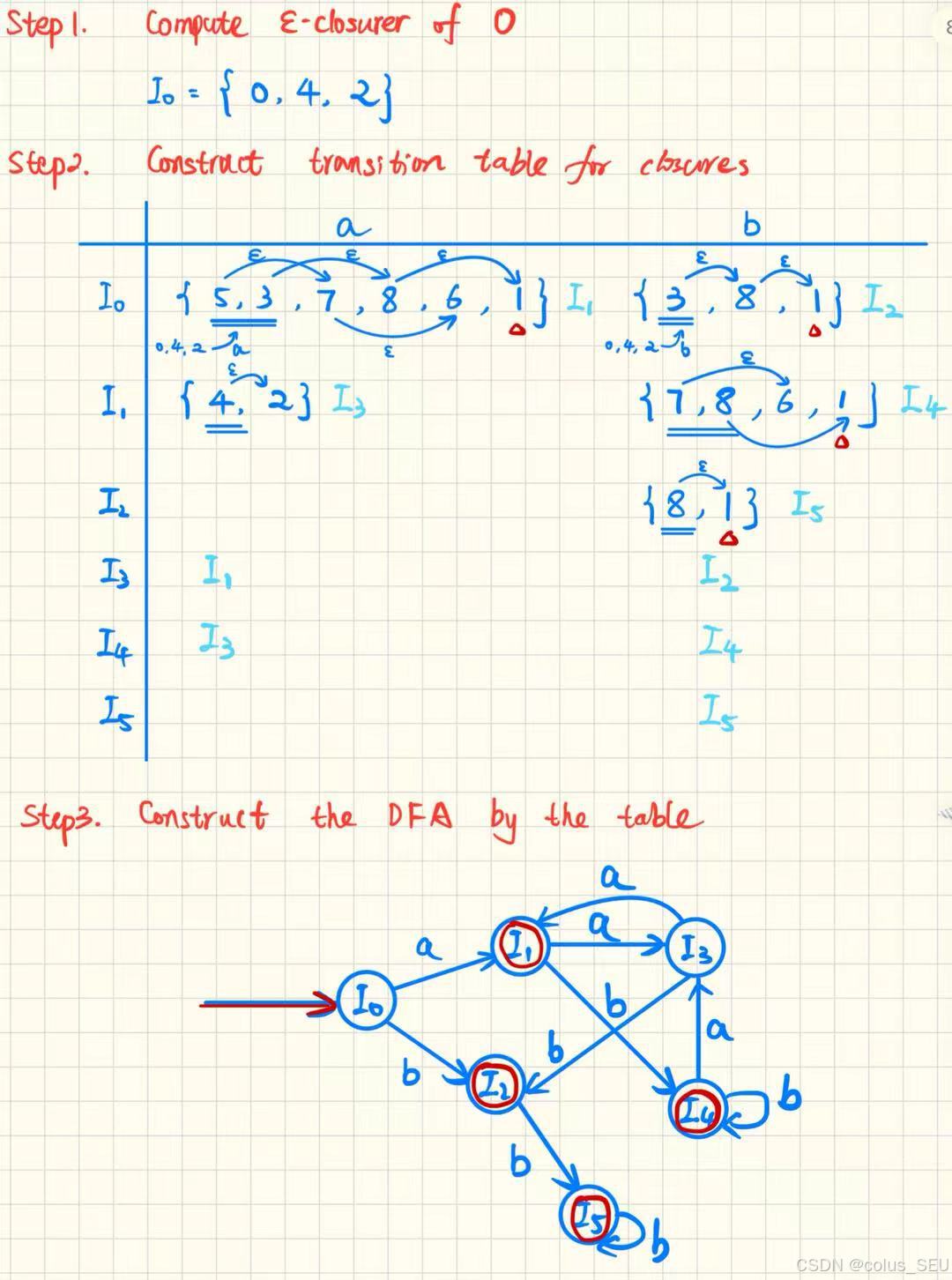
2.3 Minimal DFA

2.3.1 具体算法

算法目标

找到接受相同语言的最小状态DFA

算法步骤

1. 初始划分：{接受状态} ∪ {非接受状态}

2. 迭代细化：根据转移行为进一步划分状态组

3. 终止条件：划分不再变化

4. 选择代表：每个组选一个状态作为代表

5. 清理优化：移除死状态和不可达状态

划分规则

状态s和t在同一组，当且仅当：

• 对每个输入符号a，s和t都转移到同一组中的状态

2.3.2 例题解答

第三步最小化DFA：

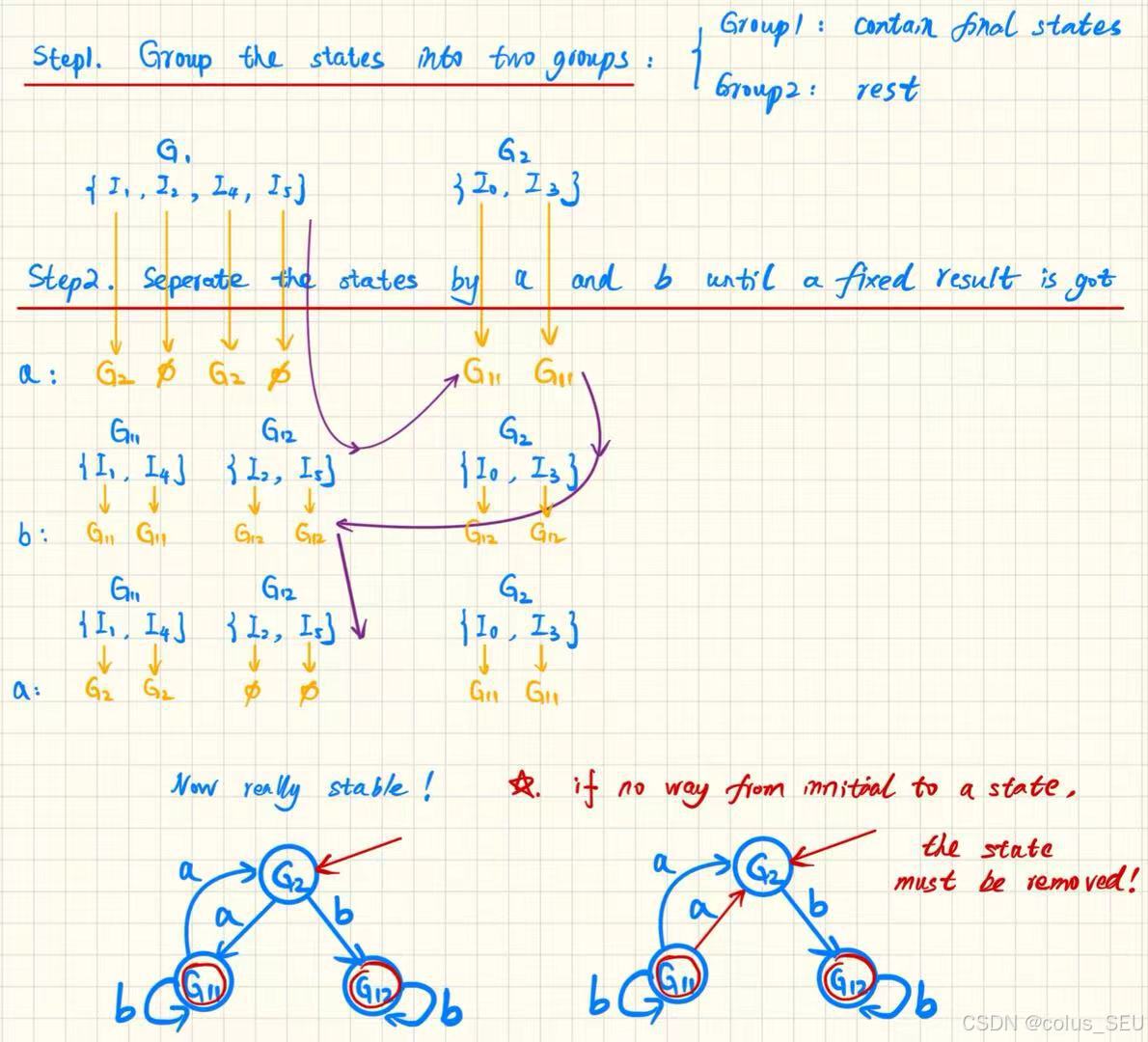
4、关键定理和性质

4.1 等价性定理

1. 任何正则表达式都可以转换为等价的NFA

2. 任何NFA都可以转换为等价的DFA

3. 任何DFA都可以找到等价的最小DFA

4. 这三种表示法描述的语言类相同（正则语言）

4.2 最小DFA的唯一性

对于任何正则语言，最小状态数的DFA在状态重命名意义下是唯一的。