当前位置：首页 > news >正文

软件设计师知识点总结：算法设计与分析

news 2025/10/28 7:08:04

一. 算法基础知识

1.1 算法的定义与特性

1.2 算法分析基础

1.2.1 时间复杂度

1.2.2 空间复杂度

二、回溯法：N 皇后问题

算法思想

问题描述

完整代码（非递归实现）

关键逻辑拆解

1. 核心变量定义

2. check函数：判断位置是否合法

3. queen函数：非递归回溯求解

递归优化

修改为递归的部分：

递归过程解释

三、分治法：最大子段和问题

算法思想

问题描述

完整代码（归并排序）

代码解释

1. Merge函数

2. MergeSort函数

3. main函数

运行结果

四、动态规划：0-1 背包问题

算法思想

问题描述

完整代码

代码解释

运行结果

五、动态规划：矩阵连乘问题

六、贪心法：部分背包问题

算法思想

问题描述

完整代码

代码解释

运行结果

七、总结

1.回溯法（Backtracking）

核心思想

经典问题：N 皇后问题

2.分治法（Divide and Conquer）

核心思想

经典问题 1：最大子段和

经典问题 2：归并排序

3.动态规划（Dynamic Programming）

核心思想

经典问题 1：0-1 背包

经典问题 2：矩阵连乘

4.贪心法（Greedy Algorithm）

核心思想

经典问题：部分背包问题

5.四大算法对比表

一. 算法基础知识

1.1 算法的定义与特性

定义：算法是对特定问题求解步骤的一种描述，是指令的有限序列，每一条指令表示一个或多个操作。
五大核心特性：
1. 有穷性：算法执行有限步骤后必须终止，不能无限循环。
2. 确定性：算法的每一步指令都有明确含义，无歧义，相同输入必产生相同输出。
3. 可行性：算法的每一步操作都能通过现有技术和工具实现。
4. 输入：算法需有 0 个或多个输入（0 个输入指算法本身确定所有初始条件）。
5. 输出：算法需有 1 个或多个输出（反映问题求解结果，无输出的算法无意义）。

1.2 算法分析基础

1.2.1 时间复杂度

定义：衡量算法运行从开始到结束所需的时间，通常以 “算法中基本操作重复执行的次数” 作为度量标准，记为T(n)（n为问题规模）。
渐进时间复杂度：当n足够大时，忽略T(n)中的低阶项和常数系数，仅保留最高阶项，记为O(g(n))。例如，T(n)=3n³+2n²+n，其渐进时间复杂度为O(n³)。
常见时间复杂度排序（从低到高）：O(1) < O(log₂n) < O(n) < O(nlog₂n) < O(n²) < O(n³) < O(2ⁿ)（O(1)为常数时间，O(log₂n)为对数时间，O(n)为线性时间，O(n²)为平方时间，O(2ⁿ)为指数时间）

1.2.2 空间复杂度

定义：衡量算法运行过程中临时占用存储空间的大小，仅考虑为局部变量分配的存储空间，记为S(n)。
示例：一个仅用几个变量的算法，空间复杂度为O(1)；一个需要存储n个元素数组的算法，空间复杂度为O(n)

二、回溯法：N 皇后问题

算法思想

回溯法本质是 “试错法”：通过递归尝试所有可能的解，当发现当前路径无法得到有效解时，退回上一步换方向继续尝试。就像走迷宫，走不通就回头换条路。

问题描述

在 N×N 的棋盘上放置 N 个皇后，要求皇后之间不能同行、同列、同对角线（互相不能攻击），找出所有可能的摆放方式。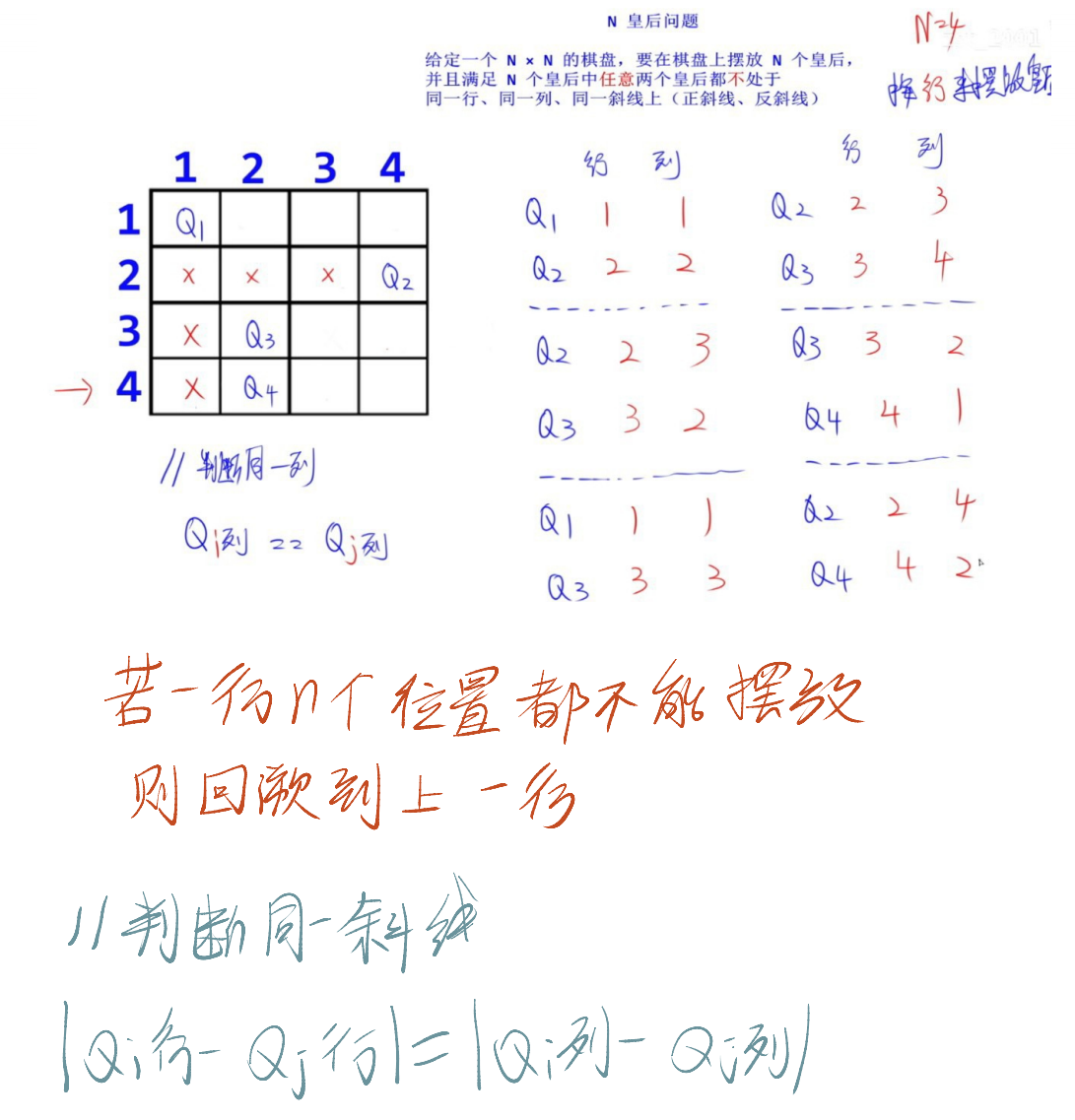

完整代码（非递归实现）

#include <math.h>
#include <stdio.h>#define N 10  // 定义棋盘大小，可修改为其他值（如4、8等）int q[N + 1];  // 存储皇后的列号，q[j]表示第j个皇后所在的列// 检查第j个皇后的位置是否合法
int check(int j) {int i;for (i = 1; i < j; i++) {// 判断是否在同一列或同一斜线上if (q[i] == q[j] || abs(i - j) == abs(q[i] - q[j])) {return 0;  // 不合法返回0}}return 1;  // 合法返回1
}void queen() {int answer = 0;  // 方案数int j = 1;       // 表示正在摆放第j个皇后// 初始化第1个皇后的位置for (int i = 1; i <= N; i++) {q[i] = 0;}while (j >= 1) {  // 回溯循环，j<1时结束q[j] = q[j] + 1;  // 让第j个皇后向后一列摆放while (q[j] <= N && !check(j)) {  // 判断第j个皇后的位置是否合法q[j] = q[j] + 1;  // 不合法就往后一个位置摆放}if (q[j] <= N) {  // 第j个皇后找到一个合法的摆放位置if (j == N) {  // 找到N皇后的一组解answer = answer + 1;printf("方案%d: ", answer);for (int i = 1; i <= N; i++) {printf("%d ", q[i]);}printf("\n");} else {j = j + 1;  // 继续摆放下一个皇后}} else {  // 第j个皇后找不到合法的摆放位置q[j] = 0;  // 还原第j个皇后的位置j = j - 1;  // 回溯到前一个皇后}}
}int main() {queen();return 0;
}

关键逻辑拆解

1. 核心变量定义

#define N 10：定义皇后数量（棋盘大小为 N×N），修改此值可求解不同规模的 N 皇后问题（如 4 皇后、8 皇后）。
int q[N + 1]：数组下标j表示 “第 j 个皇后”（对应棋盘的第 j 行），数组值q[j]表示该皇后所在的 “列号”。例如q[3] = 5表示第 3 个皇后放在第 3 行第 5 列。

2. `check`函数：判断位置是否合法

作用：检查第j个皇后的当前位置（第 j 行第q[j]列）是否与之前的j-1个皇后冲突。
逻辑：遍历前j-1个皇后（行号 1~j-1），若存在以下情况则冲突：
- 同一列：q[i] == q[j]（第 i 个和第 j 个皇后在同一列）。
- 同一对角线：行差的绝对值等于列差的绝对值（abs(i-j) == abs(q[i]-q[j])），即两点在同一条斜线上。
返回值：冲突返回 0（不合法），不冲突返回 1（合法）。

3. `queen`函数：非递归回溯求解

这是整个算法的核心，通过循环模拟递归的回溯过程，步骤如下：

（1）初始化

int answer = 0;  // 记录解的数量
int j = 1;       // 从第1个皇后开始处理
for (int i = 1; i <= N; i++) { q[i] = 0; }  // 所有皇后初始位置为0（未放置）

（2）回溯主循环（while (j >= 1)）

只要还有皇后可以调整（j >= 1），就持续尝试：

步骤 1：移动当前皇后到下一列
```
q[j] = q[j] + 1;  // 第j个皇后从当前位置+1开始尝试
```
例如：若之前q[j]是 2，现在移到 3 列；若之前是 0（未放置），则从 1 列开始尝试。

步骤 2：寻找当前皇后的合法位置

while (q[j] <= N && !check(j)) {  q[j] = q[j] + 1;  // 不合法就一直往后移
}

循环条件：列号未超过 N（q[j] <= N），且当前位置不合法（!check(j)）。
作用：让第 j 个皇后在当前行（第 j 行）不断后移，直到找到合法位置或超出棋盘。
步骤 3：根据位置合法性处理
- 情况 1：找到合法位置（q[j] <= N）
  - 若已处理完最后一个皇后（j == N）：说明找到一组完整解，输出解并计数（answer++）。
  - 若未处理完（j < N）：继续处理下一个皇后（j = j + 1）。
- 情况 2：未找到合法位置（q[j] > N）
  - 说明当前皇后在当前行无论放哪一列都冲突，需要回溯：
    - 重置当前皇后位置（q[j] = 0），避免影响下次尝试。
    - 退回上一个皇后（j = j - 1），让上一个皇后换个位置再试。

4. main函数

仅调用queen()函数启动求解过程，简洁明了。

举例理解（以 4 皇后为例）

当N=4时，程序会输出 2 组解：

方案1: 2 4 1 3 
方案2: 3 1 4 2

方案 1 表示：第 1 个皇后在 2 列，第 2 个在 4 列，第 3 个在 1 列，第 4 个在 3 列。
每一步的回溯过程：例如当第 4 个皇后找不到位置时，会退回第 3 个皇后调整位置，直到找到合法解。

通过这种非递归的回溯方式，程序高效枚举了所有可能的皇后位置，遇到冲突立即回溯，最终找出所有合法解。核心逻辑是 “尝试→检查→推进 / 回溯” 的循环，非常适合理解回溯法的本质。

递归优化

#include <math.h>
#include <stdio.h>#define N 10  // 棋盘大小（N皇后）int q[N + 1];  // q[j]表示第j个皇后的列号（行号为j）
int answer = 0;  // 解的数量// 检查第j个皇后的位置是否合法
int check(int j) {int i;for (i = 1; i < j; i++) {// 同一列或同一对角线冲突if (q[i] == q[j] || abs(i - j) == abs(q[i] - q[j])) {return 0;  // 不合法}}return 1;  // 合法
}// 递归函数：放置第j个皇后
void place(int j) {// 若已放置完第N个皇后，输出解if (j > N) {answer++;printf("方案%d: ", answer);for (int i = 1; i <= N; i++) {printf("%d ", q[i]);}printf("\n");return;  // 回溯}// 尝试第j个皇后在当前行的每一列for (int col = 1; col <= N; col++) {q[j] = col;  // 放置第j个皇后到col列if (check(j)) {  // 检查是否合法place(j + 1);  // 合法则递归放置下一个皇后}// 不合法则继续尝试下一列（自动回溯）}
}int main() {place(1);  // 从第1个皇后开始放置return 0;
}

修改为递归的部分：

用place(j)递归函数替代原queen()中的循环回溯：
- j表示当前要放置的皇后编号（对应行号j）。
- 终止条件：j > N时表示所有皇后放置完成，输出解。
递归逻辑：
- 对第j个皇后尝试每一列（col=1~N）。
- 若当前列合法（check(j)返回 1），则递归放置下一个皇后（place(j+1)）。
- 不合法则自动尝试下一列（相当于非递归中的 “调整位置”），无需手动重置变量（递归栈自动实现回溯）。

递归过程解释

以 4 皇后为例：

place(1)：处理第 1 个皇后，尝试列 1~4。
当第 1 个皇后放在列 2（q[1]=2）且合法时，调用place(2)处理第 2 个皇后。
第 2 个皇后尝试列 1~4，找到合法列 4（q[2]=4），调用place(3)。
以此类推，直到place(5)（j=5 > 4），输出第 1 组解。
递归返回后，自动尝试其他列，直到找出所有解。

三、分治法：最大子段和问题

算法思想

分治法是 “分而治之”：将复杂问题拆分成多个规模更小的子问题，递归解决子问题后，合并结果得到原问题的解。就像解决大项目时，先拆成小模块，再整合模块结果。

问题描述

在整数数组中找到一个连续子数组（可空），使其和最大。例如数组[-2,1,-3,4,-1,2,1,-5,4]的最大子段和为6（对应子数组[4,-1,2,1]）。

完整代码（归并排序）

#include <stdio.h>
#include <limits.h>  // 用于INT_MAX// 合并两个有序子数组：A[p..q]和A[q+1..r]
void Merge(int A[], int p, int q, int r) {int i, j, k;int n1 = q - p + 1;  // 左子数组长度int n2 = r - q;      // 右子数组长度int L[50], R[50];    // 临时存储左右子数组// 填充左子数组 Lfor (i = 0; i < n1; i++) {L[i] = A[p + i];}// 填充右子数组 Rfor (j = 0; j < n2; j++) {R[j] = A[q + j + 1];}// 哨兵值：确保当一个子数组遍历完后，另一个能全部填入L[n1] = INT_MAX;R[n2] = INT_MAX;i = 0;j = 0;// 合并两个有序子数组到原数组A[p..r]for (k = p; k <= r; k++) {if (L[i] <= R[j]) {A[k] = L[i];i++;} else {A[k] = R[j];j++;}}
}// 归并排序主函数（分治）
void MergeSort(int A[], int p, int r) {if (p < r) {  // 当子数组长度大于1时才需要排序int q = (p + r) / 2;  // 找到中间点MergeSort(A, p, q);   // 递归排序左半部分MergeSort(A, q + 1, r);  // 递归排序右半部分Merge(A, p, q, r);    // 合并左右两个有序子数组}
}int main() {int A[] = {4, 1, 3, 6, 7, 5, 2, 9};int n = sizeof(A) / sizeof(A[0]);  // 计算数组长度MergeSort(A, 0, n - 1);  // 对数组A[0..7]进行归并排序// 打印排序后的数组printf("排序结果：");for (int i = 0; i < n; i++) {printf("%d ", A[i]);}printf("\n");return 0;
}

代码解释

1. `Merge`函数

作用：将两个已经有序的子数组 A[p..q] 和 A[q+1..r] 合并成一个有序数组。
步骤：
- 分别将左右子数组复制到临时数组 L 和 R 中。
- 给 L 和 R 末尾添加哨兵值 INT_MAX，确保子数组遍历完后能自动填充剩余元素。
- 依次比较 L 和 R 的元素，将较小的元素放入原数组 A 中，直到所有元素合并完成。

2. `MergeSort`函数

作用：通过分治法实现归并排序。
步骤：
- 分：如果 p < r，计算中间点 q，将数组分为 A[p..q] 和 A[q+1..r] 两部分。
- 治：递归调用 MergeSort 分别对左右两部分进行排序。
- 合：调用 Merge 函数将排好序的左右两部分合并成一个有序数组。

3. `main`函数

定义测试数组 A，调用 MergeSort 对其进行排序，最后打印排序结果。

运行结果

输入数组 {4, 1, 3, 6, 7, 5, 2, 9} 经过归并排序后，输出结果为：

排序结果：1 2 3 4 5 6 7 9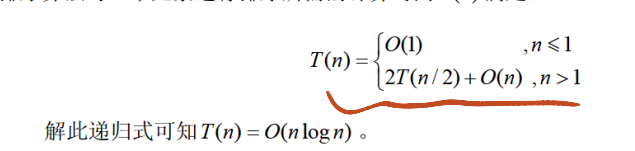

归并排序是分治法的经典应用，核心思想是 “分而治之”—— 将大问题分解为小问题递归解决，再将小问题的解合并得到大问题的解。

四、动态规划：0-1 背包问题

算法思想

动态规划通过 “存储子问题的解” 避免重复计算：利用问题的 “最优子结构”（最优解包含子问题的最优解）和 “重叠子问题”（子问题重复出现），用表格（DP 表）记录子问题结果，逐步推导最终解。

问题描述

有 n 件物品，每件物品有重量w[i]和价值v[i]，背包容量为 W。每件物品只能选一次，求装入背包的最大价值。

完整代码

#include <stdio.h>#define N 4  // 物品数量
#define W 5  // 背包容量// 求两个数的最大值
int max(int a, int b) {return a > b ? a : b;
}int main() {// 物品价值数组（v[0]无用，从v[1]开始表示第1件物品的价值）int v[] = {0, 2, 4, 5, 6};// 物品重量数组（w[0]无用，从w[1]开始表示第1件物品的重量）int w[] = {0, 1, 2, 3, 4};// 子问题解数组：f[i][j]表示前i件物品、背包容量为j时的最大价值int f[N + 1][W + 1] = {0};  int i, j;// 遍历每件物品for (i = 1; i <= N; i++) {// 遍历每种背包容量for (j = 1; j <= W; j++) {if (j >= w[i]) {  // 背包容量足够装下第i件物品// 选或不选第i件物品，取最大值f[i][j] = max(f[i - 1][j], f[i - 1][j - w[i]] + v[i]);} else {  // 背包容量不足，不能选第i件物品f[i][j] = f[i - 1][j];}}}// 输出最终最大价值（前N件物品、容量W时的最大价值）printf("%d\n", f[N][W]);// 输出子问题解数组的所有值（可选）for (i = 0; i <= N; i++) {for (j = 0; j <= W; j++) {printf("%d ", f[i][j]);}printf("\n");}return 0;
}

代码解释

宏定义与函数：
- #define N 4 和 #define W 5 分别定义物品数量和背包容量。
- max 函数用于比较两个数的大小，返回较大值。
数组定义：
- v 数组存储物品价值，w 数组存储物品重量，数组下标从 1 开始（v[0]和w[0]无用，仅为了对齐索引）。
- f 是二维数组，f[i][j] 表示 “前i件物品，背包容量为j时的最大价值”，初始化为 0。
状态转移逻辑：
- 外层循环遍历每件物品（i从 1 到N）。
- 内层循环遍历每种背包容量（j从 1 到W）。
- 若当前容量j能装下第i件物品（j >= w[i]），则选择 “不选第i件（价值为f[i-1][j]）” 或 “选第i件（价值为f[i-1][j-w[i]] + v[i]）” 中的最大值。
- 若容量不足，则只能不选第i件，价值为f[i-1][j]。
输出结果：
- 首先输出最终的最大价值f[N][W]（前 4 件物品、容量 5 时的最大价值）。
- 然后输出f数组的所有值，展示子问题的解（可选，用于理解动态规划的过程）。

运行结果

对于上述代码，最终输出的最大价值为8（选择价值为 2 和 6 的物品，重量 1+4=5，总价值 8），f数组的输出如下：

0 0 0 0 0 0 
0 2 2 2 2 2 
0 2 4 6 6 6 
0 2 4 6 7 9 
0 2 4 6 7 9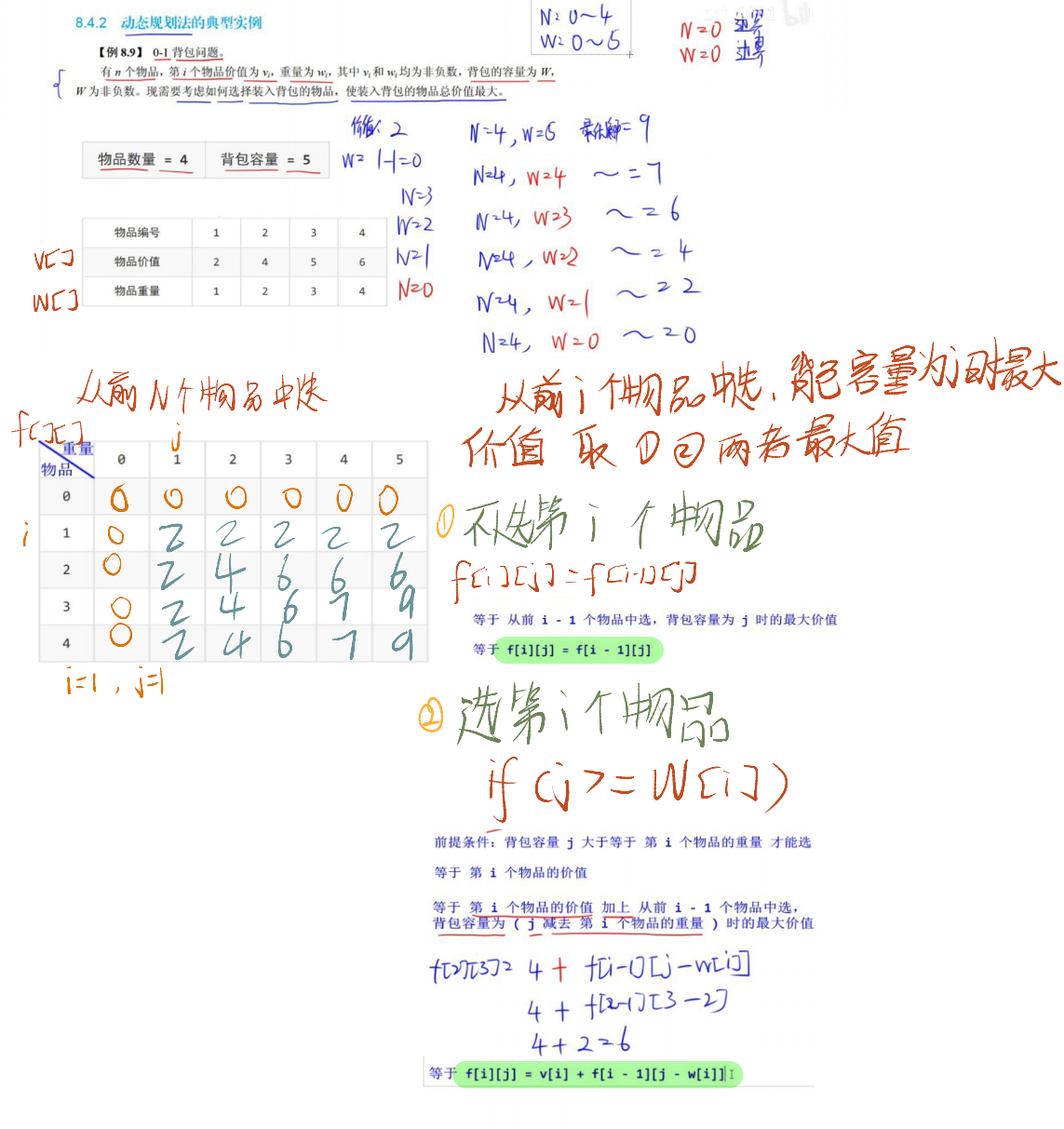

五、动态规划：矩阵连乘问题

六、贪心法：部分背包问题

算法思想

贪心法是 “局部最优→全局最优”：每一步都选择当前最优的选项（局部最优），最终得到全局最优解。适用于满足 “贪心选择性质” 的问题（局部最优能导致全局最优）。

问题描述

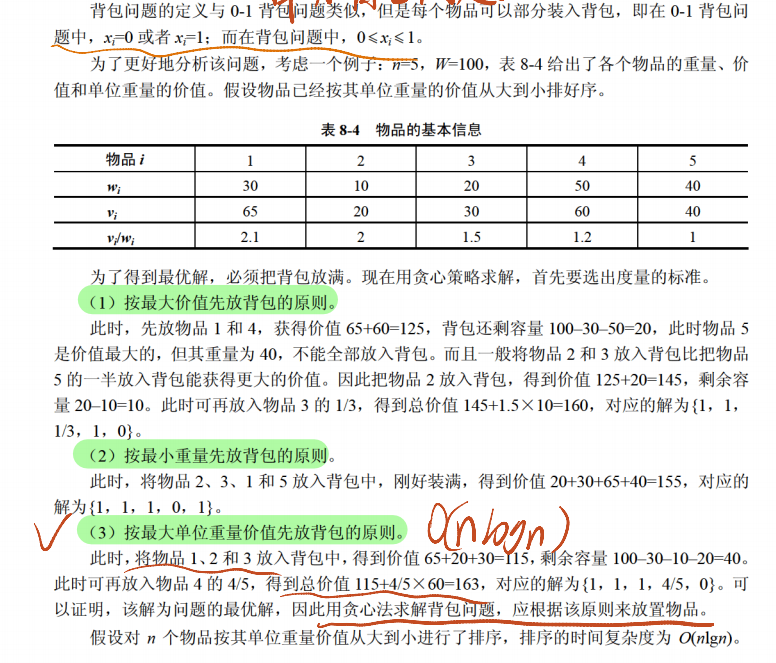
有 n 件物品，每件物品有重量w[i]和价值v[i]，背包容量为 W。物品可以分割（取一部分），求装入背包的最大价值。

完整代码

#include <stdio.h>
#include <stdlib.h>
#include <limits.h>#define N 5  // 物品数量
#define W 100  // 背包容量int v_temp[N + 1], w_temp[N + 1];  // 物品价值、重量的临时数组
double vw_temp[N + 1];  // 单位重量价值的临时数组
double answer[N + 1];  // 解决方案数组（记录每件物品装入的比例）// 归并排序（按单位重量价值降序）
void merge_sort(int v[], int w[], double vw[], int l, int r) {if (l >= r) return;  // 递归终止条件int mid = l + r >> 1;  // 计算中点（等价于(l + r) / 2）merge_sort(v, w, vw, l, mid);     // 递归排序左半部分merge_sort(v, w, vw, mid + 1, r); // 递归排序右半部分int i = l, j = mid + 1, k = l;// 合并两个有序子数组while (i <= mid && j <= r) {if (vw[i] >= vw[j]) {  // 按单位价值降序排列vw_temp[k] = vw[i];v_temp[k] = v[i];w_temp[k] = w[i];k++, i++;} else {vw_temp[k] = vw[j];v_temp[k] = v[j];w_temp[k] = w[j];k++, j++;}}// 处理剩余元素while (i <= mid) {vw_temp[k] = vw[i];v_temp[k] = v[i];w_temp[k] = w[i];k++, i++;}while (j <= r) {vw_temp[k] = vw[j];v_temp[k] = v[j];w_temp[k] = w[j];k++, j++;}// 将临时数组复制回原数组for (int p = l; p <= r; p++) {vw[p] = vw_temp[p];v[p] = v_temp[p];w[p] = w_temp[p];}
}// 显示物品价值、重量、单位重量价值数组
void show(int v[], int w[], double vw[]) {for (int i = 1; i <= N; i++) {printf("物品%d: 价值%d, 重量%d, 单位价值%.2f\n", i, v[i], w[i], vw[i]);}
}// 求解部分背包的最大价值
double Max_Value(int v[], int w[], double vw[]) {double result = 0.0;int i;int W_temp = W;  // 剩余背包容量// 初始化解决方案数组for (i = 1; i <= N; i++) {answer[i] = 0.0;}// 贪心选择：优先装单位价值高的物品for (i = 1; i <= N; i++) {if (W_temp >= w[i]) {  // 能装下整个物品answer[i] = 1.0;result += v[i];W_temp -= w[i];} else {  // 只能装部分break;}}// 装剩余容量的部分物品if (W_temp > 0 && i <= N) {answer[i] = (double)W_temp / w[i];result += W_temp * vw[i];  // 或 result += answer[i] * v[i];}return result;
}int main() {int v[] = {0, 6, 3, 3, 5, 4};  // 物品价值数组（v[0]无用）int w[] = {0, 2, 2, 6, 5, 4};  // 物品重量数组（w[0]无用）double vw[N + 1];  // 单位重量价值数组// 计算单位重量价值for (int i = 1; i <= N; i++) {vw[i] = (double)v[i] / w[i];}printf("排序前：\n");show(v, w, vw);// 按单位重量价值降序排序merge_sort(v, w, vw, 1, N);printf("\n排序后：\n");show(v, w, vw);// 求解最大价值double result = Max_Value(v, w, vw);printf("\nresult = %.1lf\n\n", result);// 输出解决方案printf("解决方案结果：\n");for (int i = 1; i <= N; i++) {printf("物品%d 装入比例: %.1lf\n", i, answer[i]);}return 0;
}

代码解释

归并排序 merge_sort：
- 递归将数组分成左右两部分，分别排序后合并。
- 合并时按单位重量价值 vw 降序排列，确保后续贪心选择时优先选性价比高的物品。
- 使用临时数组 v_temp、w_temp、vw_temp 存储中间结果，最后复制回原数组。
显示函数 show：
- 用于打印物品的价值、重量和单位重量价值，方便观察排序前后的变化。
核心求解函数 Max_Value：
- 初始化剩余背包容量 W_temp 和解决方案数组 answer。
- 遍历物品，优先装入单位价值高的完整物品；若剩余容量不足，则装入部分物品。
- 通过 answer 数组记录每件物品的装入比例，最终返回最大价值。
主函数：
- 定义物品价值、重量数组，计算单位重量价值并排序。
- 调用 Max_Value 求解最大价值，最后输出解决方案。

运行结果

代码运行后会输出排序前后的物品信息、最大价值以及每件物品的装入比例，例如：

排序前：
物品1: 价值6, 重量2, 单位价值3.00
物品2: 价值3, 重量2, 单位价值1.50
物品3: 价值3, 重量6, 单位价值0.50
物品4: 价值5, 重量5, 单位价值1.00
物品5: 价值4, 重量4, 单位价值1.00排序后：
物品1: 价值6, 重量2, 单位价值3.00
物品2: 价值3, 重量2, 单位价值1.50
物品4: 价值5, 重量5, 单位价值1.00
物品5: 价值4, 重量4, 单位价值1.00
物品3: 价值3, 重量6, 单位价值0.50result = 110.0解决方案结果：
物品1 装入比例: 1.0
物品2 装入比例: 1.0
物品4 装入比例: 1.0
物品5 装入比例: 1.0
物品3 装入比例: 0.0

七、总结

1.回溯法（Backtracking）

核心思想

通过递归 / 栈尝试所有可能解，当发现当前路径无效时回溯（退回上一步换方向），本质是 “穷举 + 剪枝”，避免无效搜索。

经典问题：N 皇后问题

问题：在 N×N 棋盘放置 N 个皇后，使皇后间不同行、列、对角线。
时间复杂度：
- 最坏情况：需尝试所有可能的列位置，时间复杂度为 O(N!)（N 的阶乘）。
- 实际因剪枝（冲突检查）会低于 N!，但仍为指数级。
空间复杂度：
- 递归实现：递归栈深度为 N（行数），存储皇后位置的数组大小为 N，故空间复杂度为 O(N)。
- 非递归实现（栈模拟）：栈最多存储 N 个状态，每个状态需 O (N) 空间，总空间复杂度仍为 O(N²)（最坏情况）。

2.分治法（Divide and Conquer）

核心思想

将问题分解为规模更小的子问题，递归求解子问题后合并结果，核心是 “分→治→合”。

经典问题 1：最大子段和

问题：找数组中连续子数组的最大和。
时间复杂度：
- 分解为 2 个规模为 n/2 的子问题，合并步骤（计算横跨中点的和）需 O (n)，故递推式为 T (n) = 2T (n/2) + O (n)，解得 O(n log n)。
空间复杂度：
- 递归栈深度为 log n，额外空间为 O (1)，总空间复杂度 O(log n)。

经典问题 2：归并排序

问题：对数组进行排序。
时间复杂度：
- 分解为 2 个 n/2 的子问题，合并需 O (n)，递推式 T (n) = 2T (n/2) + O (n)，解得 O(n log n)（最坏 / 平均 / 最好均为此值）。
空间复杂度：
- 需额外 O (n) 空间存储临时数组，递归栈深度 O (log n)，总空间复杂度 O(n)。

3.动态规划（Dynamic Programming）

核心思想

利用问题的重叠子问题（子问题重复出现）和最优子结构（最优解包含子问题最优解），通过DP 表存储子问题解，避免重复计算。

经典问题 1：0-1 背包

问题：n 件物品，每件有重量和价值，背包容量 C，每件仅选一次，求最大价值。
时间复杂度：
- 二维 DP 表需遍历 n 件物品和 C 容量，时间复杂度 O(n×C)。
空间复杂度：
- 二维 DP 表空间为 O (n×C)；优化为一维 DP 表后，空间复杂度可降为 O(C)。

经典问题 2：矩阵连乘

问题：n 个矩阵连乘，求最少乘法次数。
时间复杂度：
- DP 表为 n×n，填充表时需三重循环（i, j, k），时间复杂度 O(n³)。
空间复杂度：
- 存储 DP 表需 O (n²)，总空间复杂度 O(n²)。

4.贪心法（Greedy Algorithm）

核心思想

每一步选择局部最优解，最终得到全局最优解，适用于满足 “贪心选择性质” 的问题（局部最优能导致全局最优）。

经典问题：部分背包问题

问题：n 件物品可分割，选物品使总价值最大（背包容量 C）。
时间复杂度：
- 需先按单位价值排序（如归并排序 / O (n log n)），再遍历物品（O (n)），总时间复杂度 O(n log n)。
空间复杂度：
- 存储物品信息和排序临时空间，总空间复杂度 O(n)。

5.四大算法对比表

算法	核心思想	典型时间复杂度	典型空间复杂度	适用场景
回溯法	试错 + 回溯	O (N!) 或指数级	O (N) 或 O (N²)	解空间小的组合问题（如 N 皇后）
分治法	分→治→合	O (n log n) 或 O (n³)	O (n) 或 O (log n)	可分解为子问题的问题（排序、最大子段和）
动态规划	存储子问题解	O (n×C) 或 O (n²)	O (n×C) 或 O (n)	有重叠子问题和最优子结构（背包、矩阵连乘）
贪心法	局部最优→全局最优	O (n log n) 或 O (n)	O(n)	满足贪心选择性质的问题（部分背包、哈夫曼编码）