三维视觉:原理与实践(课程笔记-相机模型与标定)
三维视觉:原理与实践(课程笔记-相机模型与标定)
相机模型与标定
- 相机模型
1.1 为什么需要相机标定
图像只是三维世界的2D投影
能否从2D图像恢复世界的三维信息(多视角)
如何精确的的3D物体?图像的失真如何恢复?
1.2 相机模型
薄凸透镜
边缘薄中央厚,对光线具有会聚作用
主光轴:过透镜两表面曲率中心的直线
光心:薄透镜的中心(当厚度趋于0时,两个表面顶点重合于光心)
薄凸透镜特点
经过物点,平行于光轴的光线,经过透镜后,射向像方焦点
经过物点和光心的光线,方向不变
经过物点和物方焦点的光线,经过透镜后,平行于光轴射出
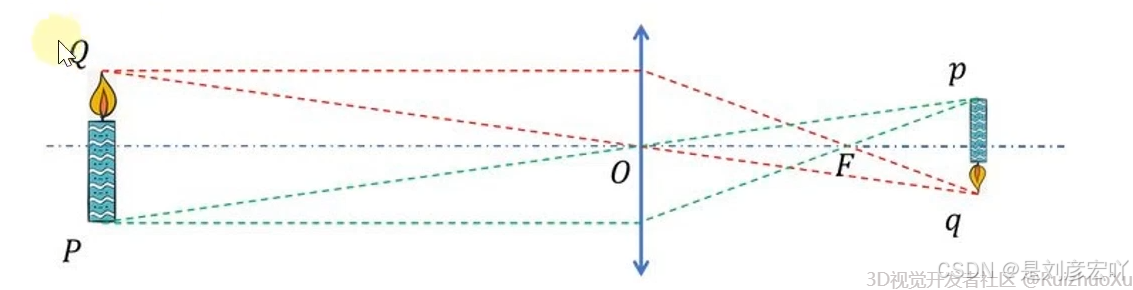
通过光心的光路来代表成像光路,对相机成像过程简化
不考虑像差
不考虑景深(假定都能清晰成像)
薄透镜
与针孔相机成像原理相似,把简化后的相机成像模型,称为针孔相机模型
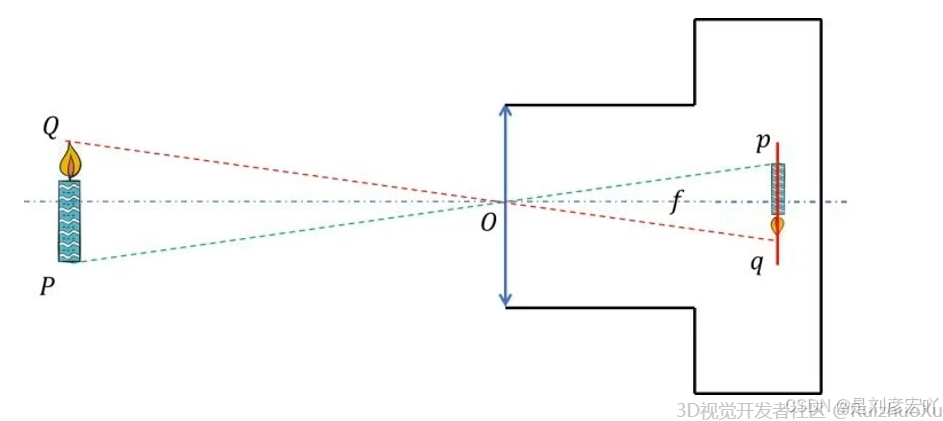
1.3 坐标系及坐标系转换关系

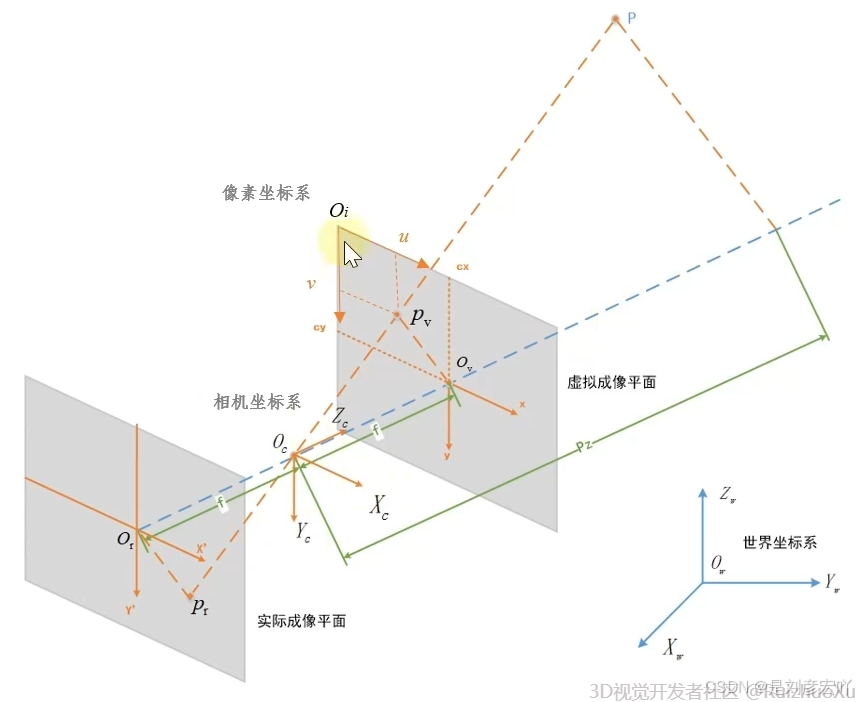
虚拟成像面到光心的距离和实际成像面到光心的距离相等
转换关系
世界坐标系——>相机坐标系:(刚体变换)
.
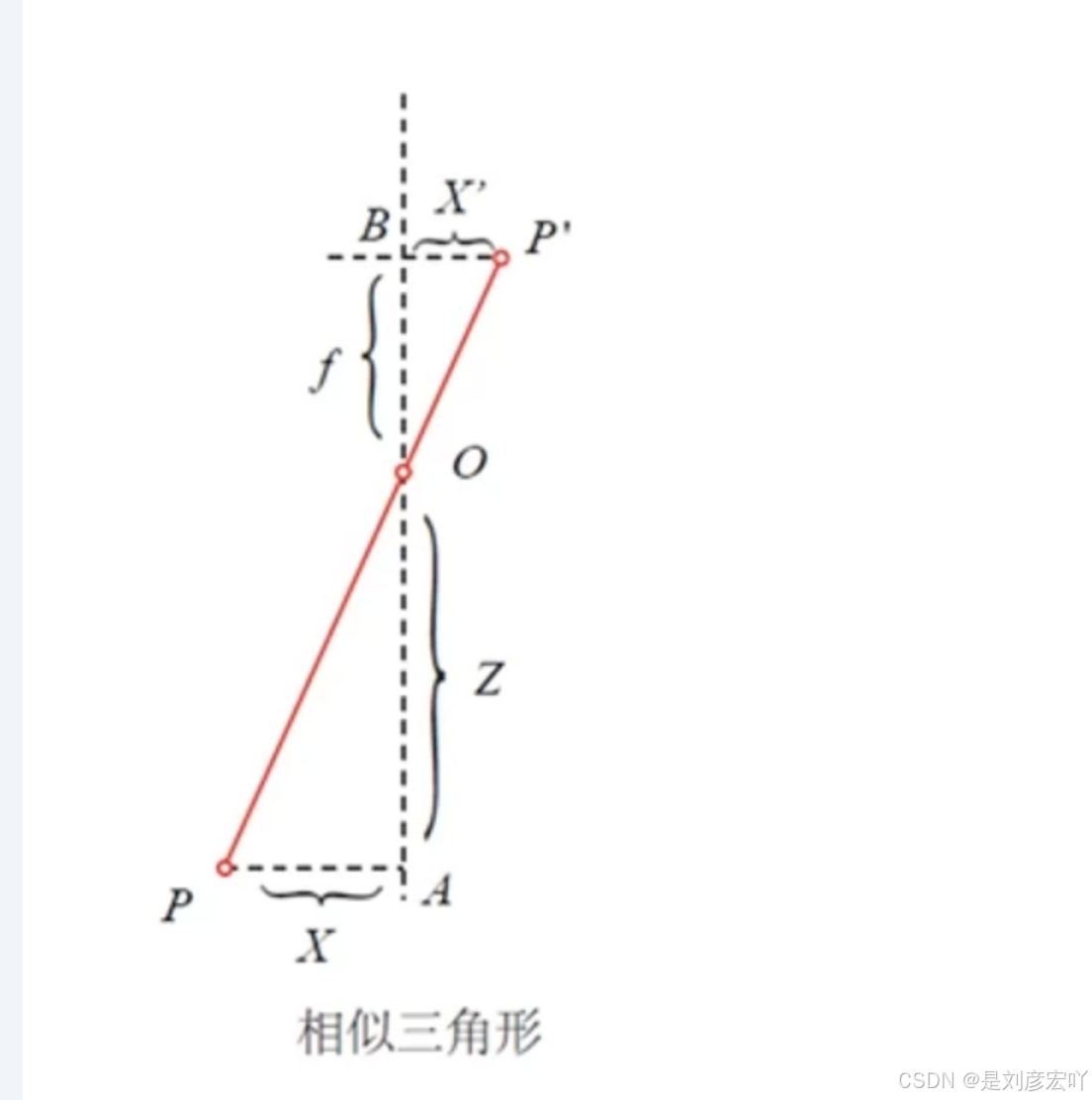


1.4 镜头畸变
畸变原因:理想的成像点于实际成像点并不重合,存在像差。畸变是单色光学像差中的一种,也是唯一不会改变成像清晰度的像差。
不同波长畸变曲线也不同
透镜的畸变主要分为径向畸变和切向畸变
径向畸变:
枕形畸变(正畸变)和桶形畸变(负畸变),且越向透镜边缘移动径向畸变越严重,是中心对称的。
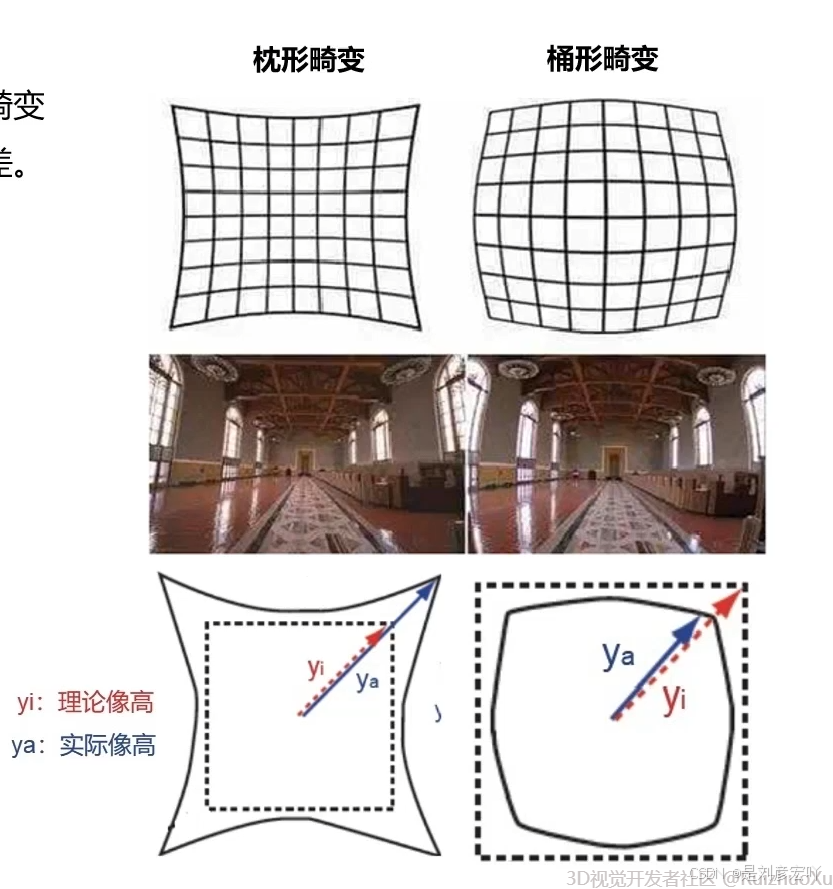
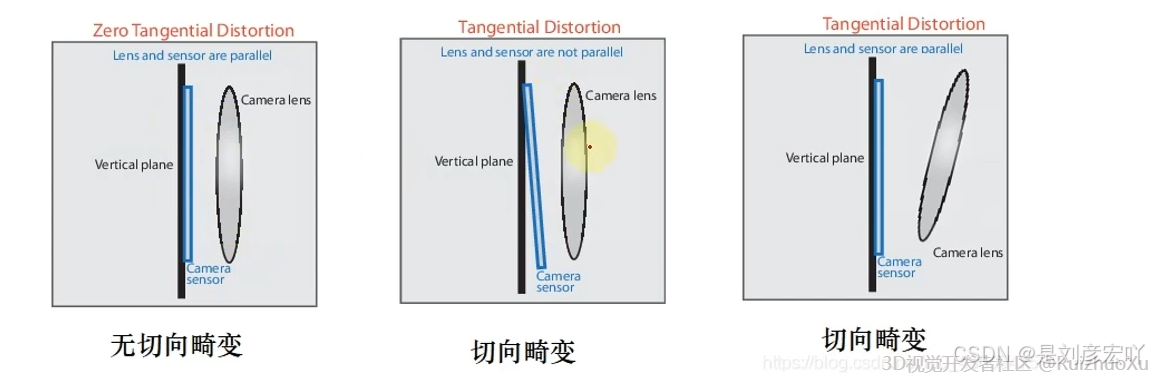


2.标定算法
2.1 张正友标定法
优化目标
目标函数:



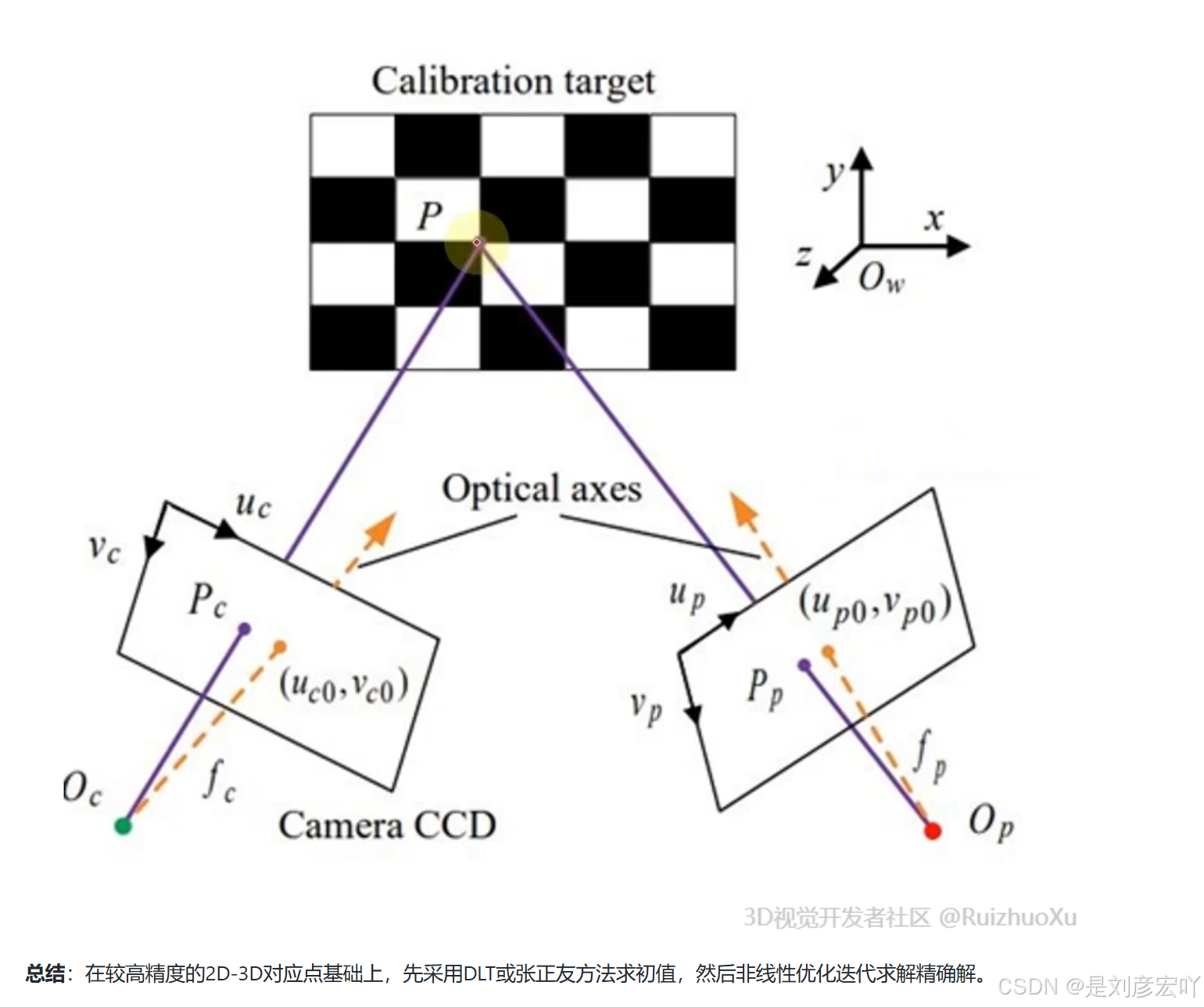
3. 标定实践
3.1 标定板
标定板的基本要求:
标定板的精度(平整度)
标定板的稳定性:降低温度膨胀系数
标定板的均匀性(背光性)
Pattern设计:
便于特征点提取(如角点或者圆心)
特征点的坐标无歧义
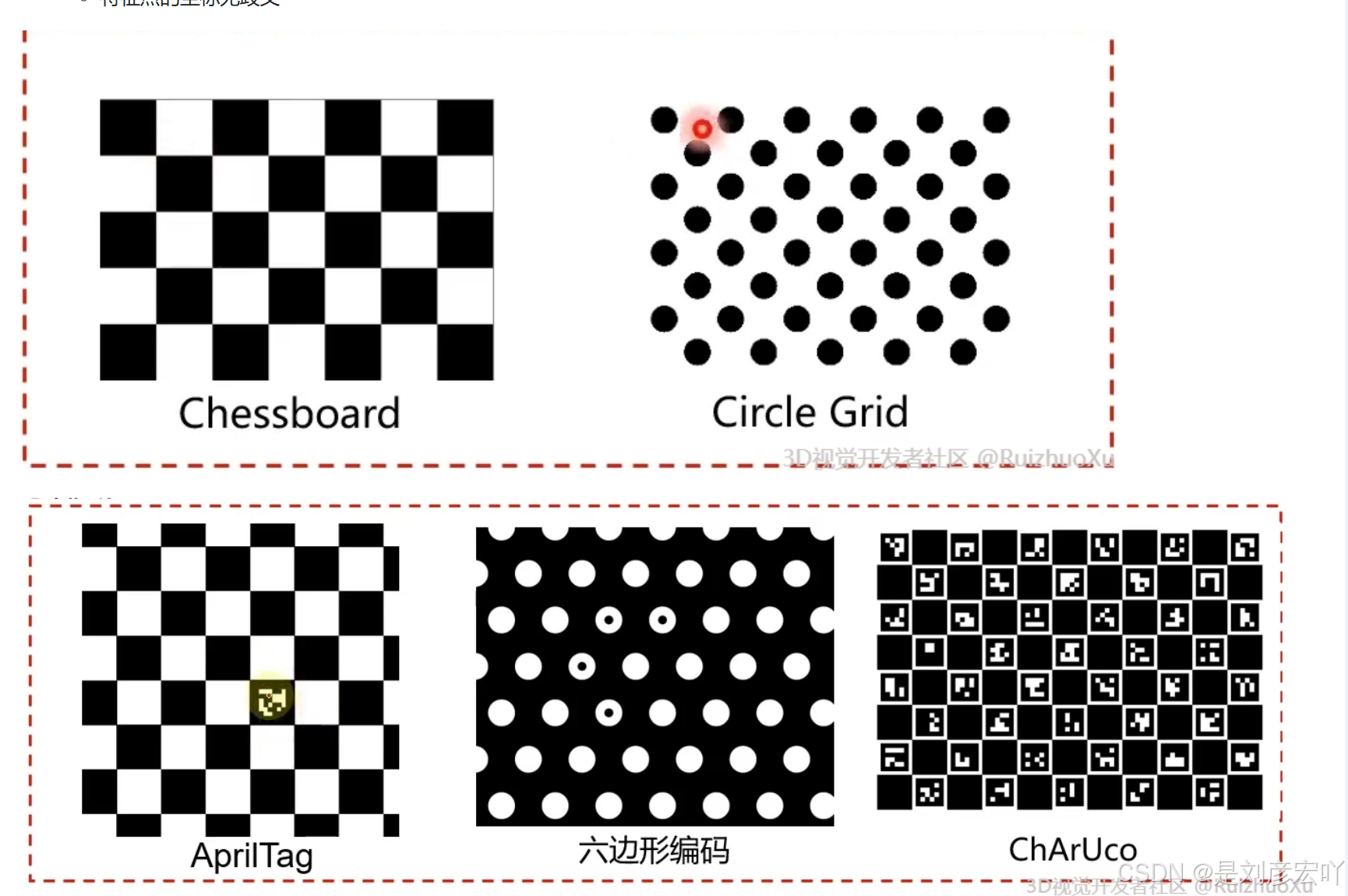
一般来讲,圆形(或圆环)标定板的提取精度高于棋盘格的提取精度。(圆心定位比较精确)
3D世界中的圆投影到2D平面中时可能会变成一个椭圆,此时圆的圆心和椭圆的圆心不对应,会带来偏心误差。
3.2 标定步骤
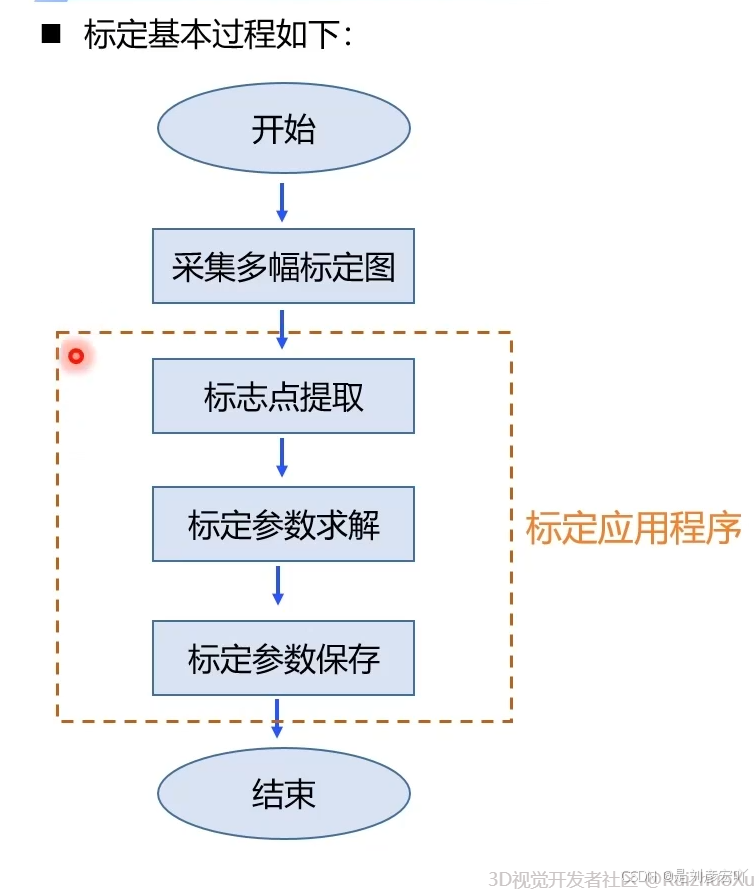
3.3 标定结果评估
标定结果的评判:
精度方面:
重投影误差(仅供参考)
对于双目:我们可以采用极线校正的精度进行评估
在结构光中:图像校正的精度
针对标准件的3D重建的精度(例如标定板)
鲁棒性方面。
4. 标定应用
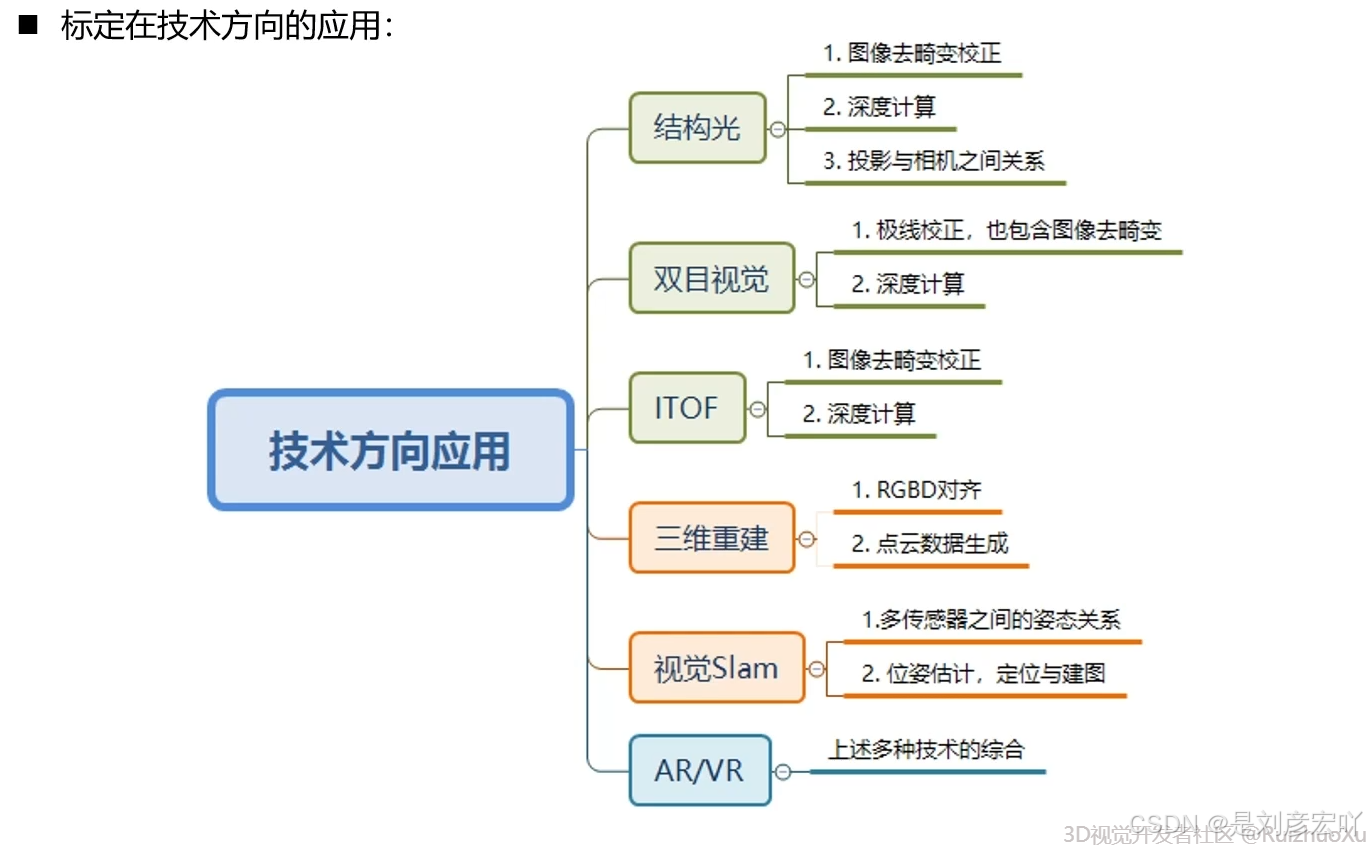
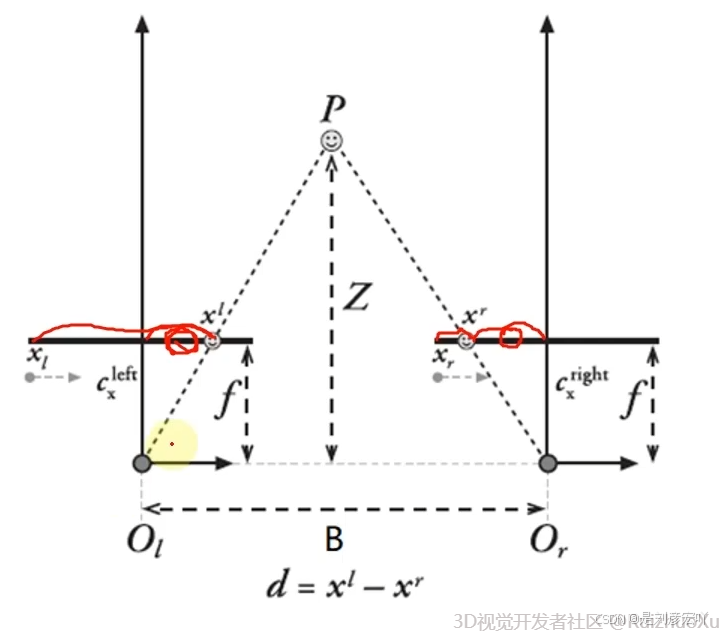
4.1 双目极线校正
理想的双目系统:
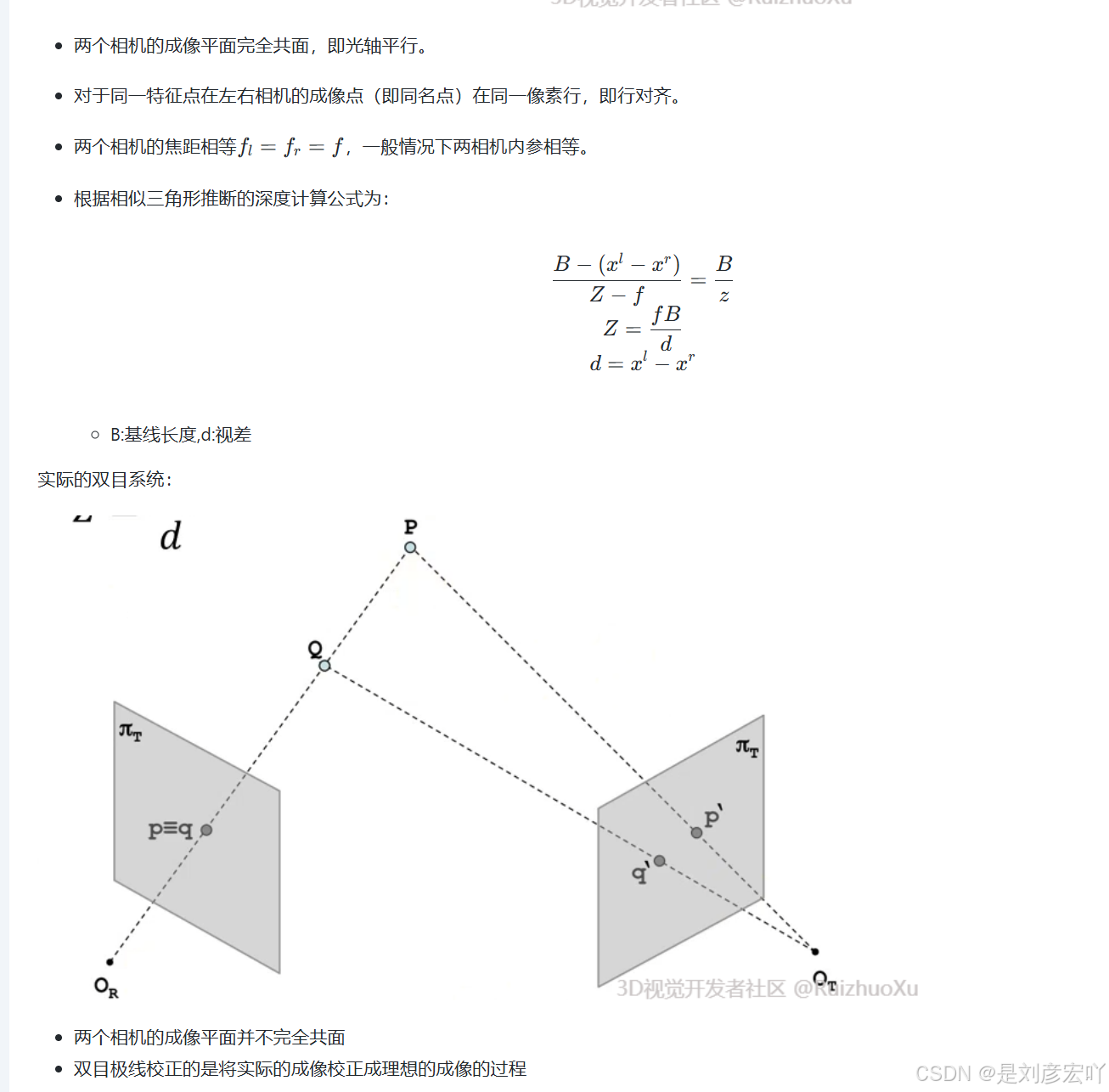
三维视觉:原理与实践(1.5节课程笔记-图像几何变换)
