云台和雷达标定方法

云台和雷达标定

最近在项目上遇到了雷达和云台的标定，即：

雷达安装在云台上，你不知道雷达光芯到云台轴心坐标的变换矩阵。

这时候，可以通过标定的方法，通过多组方程计算出这个变换矩阵。

几点感悟

• 1-你得建立统一的标准
  这一点很重要，后面会讲到，你云台的制造标准可能和机器人相关标准不同，如果你没有建立统一的标准，那么，包出错的，搞标定就是搞矩阵，矩阵中A@B和B@A是完全不一样的。这里的标准，包括坐标系的的统一，旋转方向与正负的统一，以及其他的一些标准的统一。

• 2-坐标系很重要
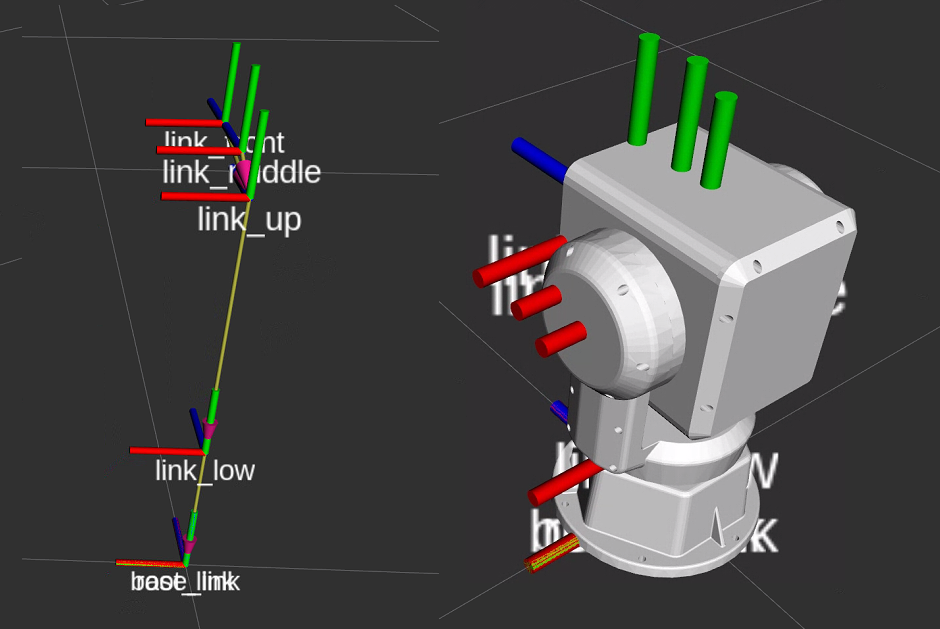
  坐标系的建立，关系着二轴云台的水平俯仰轴，关系着计算RPY的3*3的矩阵，比如我这里，我在观察云台的solidworks结构的时候，发现，它朝前是z，朝上是y，朝左是x。但是我使用的是朝前是x，朝左是y，朝上是z。这时候，你需要做的是，选定一个标准，比如我用的是朝前是x，朝左是y，朝上是z，那我写代码的时候，全程按照这个标准来计算，这时候，如果我水平旋转，就是绕着z轴旋转，如果我俯仰旋转，就是绕着y轴旋转。如果你选择朝前是z，朝上是y，朝左是x，那么水平旋转的时候，那么就是绕着y轴旋转，俯仰旋转的时候，就是绕着x轴旋转。此时，你使用的旋转矩阵就是不一样的。

• 3-对RPY以及转动正负需要了解
  这种图讲解的就很好，很直观，以前我都懒得记这个，现在，根本不用看，我就知道RPY对应的是滚转，俯仰，水平转动，因为最近用的实在是太多了。
  
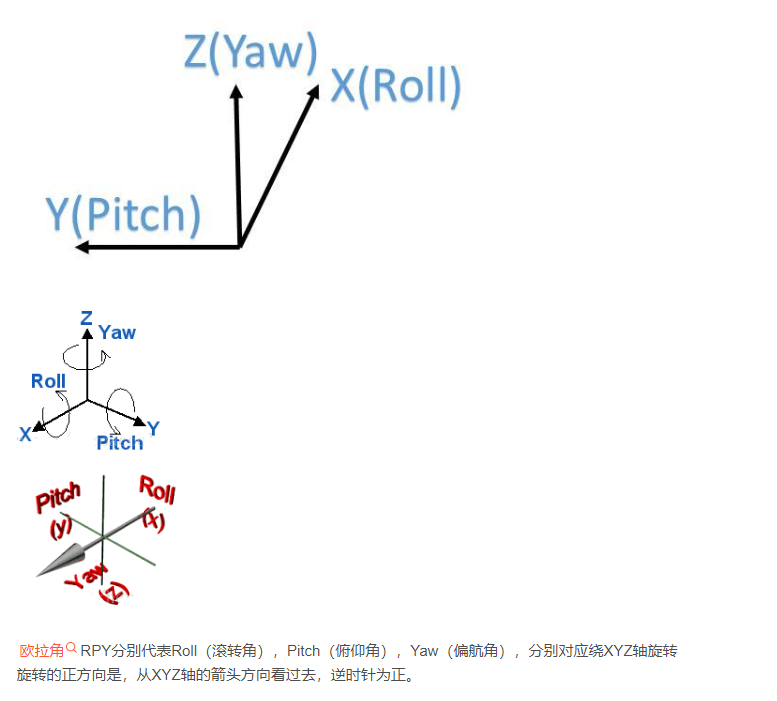
  RPY对应着滚转，俯仰，水平。

  在我这个项目中，这个厂家做的云台，和机器人相关的标准不太一样，以朝前是x，朝左是y，朝上是z作为坐标系，如果是水平向左转的话，RPY中Y应该是正的，但是现实的云台中，其向左转是负的，向上转动的话，RPY中P应该是负的，但是云台中向上转动就是正的。此时，你需要取负才对，才能符合你建立的坐标系。

  在讲详细些，云台是会提供上位机的，其上位机中调整云台上下左右的正负，和机器人中的RPY对应的正负是反过来的，由于我是按照机器人建立的坐标系，相应的就要取负过来，否则，就会导致算错。

• 4-矩阵乘法不能反，矩阵链式不能断
  这一点也是深刻的体会，目前AI很发达，这部分矩阵链式的代码，最初是AI给我写的，导致最后一直有问题，排除很多错误后，我最后把问题定位在矩阵乘法这里。
  
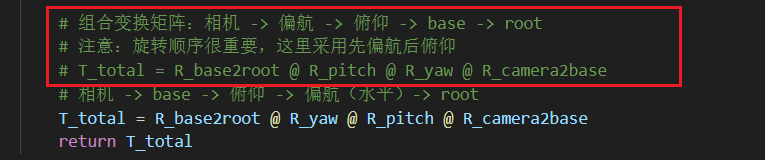
  才发现，AI给我的矩阵写反了，我后面改正后，才对了。

  因此这种链式相乘的矩阵，你千万不可给他乘反，尤其他还不是单位矩阵。

  当时我们采集了单轴旋转的数据，放到这里来测试，结果是没问题的，但是双轴旋转的数据进行测试，立马就不行了，当时也是没有考虑到这个矩阵乘法，一直想着，我需求和AI说清楚了，代码应该就没啥问题了，而且单轴测试过了，是对的。

  结果就是，单轴旋转的话，其中有个矩阵是单位矩阵，不管乘在左边还是右边，都不影响计算。双轴的话，问题就大了。

• 5-别被表象迷惑
  有些时候，你yaw和pitch的矩阵乘反了，然后你得到的相机到俯仰轴之间的变换矩阵，测试数据的时候，发现数据大致拟合出来，觉得感觉应该是对的，但是我要告诉你的是，这种情况，它可能也是你的yaw和pitch的矩阵乘反了，因为这个矩阵是你通过现有数据拟合出来的，会贴近这些数据，你可以没有用来拟合的数据进行测试一下，如果数据偏差很大，那可能你的矩阵这边，还是存在问题。

• 6-你需要有抽象建模的能力
  现实的模型是复杂的，你需要给他抽象出来，也就是你的空间能力需要不错的，然后如果可以的话，借助仿真的工具，比如ROS中的Gazebo，Mujoco这类仿真引擎（不知道引擎这个词对不对），给他设置一个真值，通过你的算法进行验证。

• 7-说说理想情况
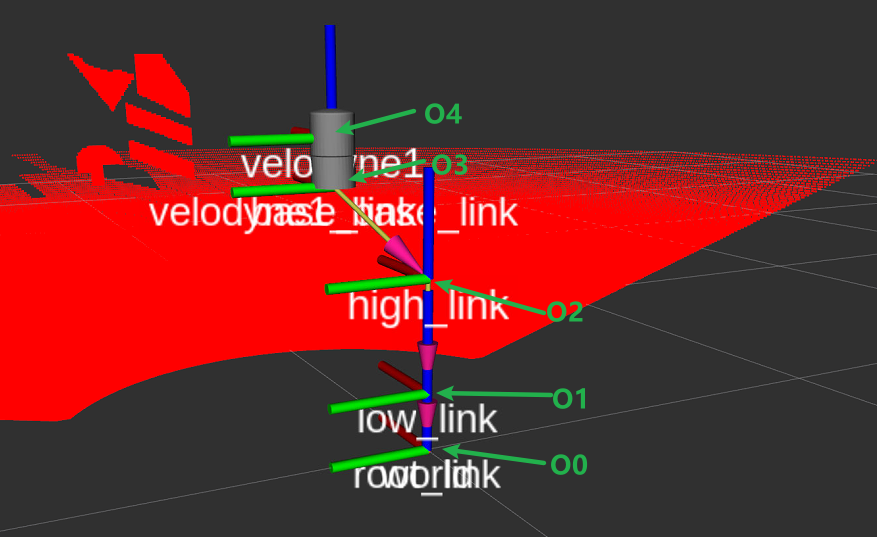
  在理想的情况，也就是上图中O0O1O2坐标系是在一条线上的，而且是相互不相交的，然后O3也就是雷达的底座，随便找个位置放，然后O4也就是雷达的光芯，其实也无所谓在哪。只需要O4和O2之间是固定的，此时，如果你采集数据进行计算，在这种情况下，无论你是单轴采集的数据，还是双轴采集的数据，只需要8组（我没有试过比这还少的情况）数据，你就能够算出这个旋转变换矩阵，无论是单轴动还是双轴动，这个我在仿真中进行了实验。

• 8-搞清楚矩阵的变量是多少个
  3D 空间的刚体变换场景下，虽然这个变换矩阵是4*4大小的，但是变换矩阵对应的独立参数确实是 6 个 ——3 个旋转参数（描述姿态）和 3 个平移参数（描述位置），也就是Rx,Ry,Rz和tx,ty,tz。

  [ R     | t ]  其中 R是3x3旋转矩阵（有3个独立参数），t是3x1平移向量（3个独立参数）
  [ 0 0 0 | 1 ]  最后一行是固定的[0,0,0,1]，无独立参数
  

• 9-当你相信你的配准精度后，如果标定结果不够理想，合理怀疑厂家设备问题
  当你排除很多问题后，最后效果还是不够理想，你该怀疑厂家的设备了，下面这种标定方法的标定，只能适用于水平旋转轴和垂直旋转轴是

• 10-设备结构不同，遇到的问题就有可能不同，不要一上来就使用别人的代码
  别人的代码，适用于别人的结构，不一定适用于你项目的结构，而且，人家的代码，你不清楚人家考虑到哪种程度。
  比如我这的云台，靠近底座的是控制水平旋转的，靠近相机的是控制俯仰的，万一别人的结构是类似机械臂的结构，靠近底座的是控制俯仰的，靠近相机的是控制水平旋转的，那么，代码就需要更改了。而且，你也不清楚，人家的转动角度，我最开始遇到的问题，就是上面第三点情况，直到我完整统一了坐标系，RPY，RPY旋转的正负都为机器人坐标系，把云台设计的标准，转到机器人上来，这时候，很多东西虽然是反正的，但是知道要怎么写了。

• 11-多试
  矩阵这个东西，如果你理论并不是很好，就需要多试试，相当于穷举法。

标定方法介绍

我们这款3D相机，它能够采集图像和点云，但是图像的分辨率很差，只有640*640，我们觉得用图像进行标定，几乎是不太行的，不知道有没有做过这方面的，点评一下这个分辨率下是否可以做。

但是这个相机采集的点云，在4米以内，质量还是不错的，因此我们采用的是点云进行标定。

这里我们采用的是0.5*0.5米的标识板，上面带有不同图案，使得后续配准结果唯一。然后标识板放在离相机2米远的位置。相机放置在云台上，这个云台的精度为0.01度。

数据采集

首先就是云台通过水平/俯仰转动，带动相机，采集多组数据，记录下每次水平/俯仰转动的大小。

对采集的数据进行数据分割，只剩下标识板部分。

点云配准

将采集到的数据和标识版标准点云进行配准，然后在标准版标识点云中，选择一个点，计算这个点，在配准过去后的点的三维坐标，这里其实就是算的是目标点P在当前设备坐标系下的坐标。这个配准，理论上来说，数据只要够好，配准就没啥问题。

然后把这些配准过去得到的点也记录下来。

计算

在1号位置下，记录的水平角度α1和俯仰角度β1，在1号位置下，配准得到的那个点p1。
在2号位置下，记录的水平角度α2和俯仰角度β2，在2号位置下，配准得到的那个点p2。

另X为O3到O2的固定的旋转变换矩阵，就可以列出下面的等式。

O1到O0的，只会受到α的影响，O2到O1的，只会受到β的影响。
α和β每次转动的时候，你也是都知道的，也就是说，左边的两个矩阵，你都能计算出来，记为A，那么现在就是相当于求解：

$$A_1@X@P_1=A_2@X@P_2$$

其中，@代表的就是矩阵乘法（我只知道python中是这样的）

通过联立多个方程组，就能把X求解出来。

算出来后，你把这里的P换成点云中的每个点，就能换到初始姿态下的点云了，实现了多个姿态下的点云，合并到一个坐标系中了。

当然，这只是原理，代码的话，可以拆分成以下三步。

├── 1计算o2到o0的旋转变换矩阵.py
├── 2计算相机到base的矩阵.py
├── 3批量验算水平俯仰.py

后续也会将代码放在GitHub上。

遇到的问题

做到这里的话，我们觉得自己的配准，没啥大问题，然后就陷入了沉思，因为仿真中的数据，用我们的标定算法，所有视角下的标识板点云，都是重合在一起的，角度误差为0°，可能很少有个别是0.01°，而且仿真中，我能够得到真值，也就是雷达光芯到O2的旋转变换矩阵，当使用8组水平旋转的数据，拟合出来的旋转变换矩阵，和真值差别很小很小。但是现实效果，就是标识板平面之间存在0.1°到1°的随机性角度误差，这不符合我们的精度要求。

然后我们就开始进行O2到O0之间的矩阵拆解，过程也挺痛苦的。

最后我试验出，如果只是把O1的坐标系摆歪，而不去改变O2和O1的轴同向且平行关系，上面的标定方法中的$$A_1@X@P_1=A_2@X@P_2$$ 是不会影响的，因为这个是乘在A矩阵左边的，不会参与到上面的标定过程中。

当你把O2坐标系摆歪后，然后再用这种方法去计算，仿真的数据，就像实际的数据一样，开始存在平面与平面之间的角度误差和位移偏差了。

也就是说，O2和O1的坐标系，一旦不是同向且平行的，他们之间，就存在一个旋转变换矩阵，需要先将O2摆正才行。

此时就是A矩阵中间，需要添加一个未知矩阵，相当于整个方程组需要算两个未知矩阵，这个在仿真中，经过计算，通过采集一些数据，验证了这个思路的正确性。

但是到现实中，又出问题了，效果还是不佳。

未完。。。。

最后

• 云台和雷达继续标定，网上很少搜到好用的教程，更多的就是手眼标定那一套，甚至有些就是人直接用手抬着标识板，不可避免标识板发生移动，导致结果肯定会不精准。

• 我们这个的精度，需要是标识板的平面夹角小于0.1度，所以很难呀。

• 上面的很多结论，是从仿真中经过验算得到的，出问题的可能性还是比较小的，但是不排除出错的可能性，笔者水平也有限，见谅。

• 我在GitHub上搭建了类似云台的水平旋转和俯仰旋转的机械结构的ROS的Gazebo仿真，可以帮助你验证很多很多情况，我靠这个，已经得出了很多结论。
  https://github.com/Knighthood2001/gimbal_structure_simulation
  上面这个是我主要使用的， 它搭载了仿真雷达， 可以用来采集仿真数据。
  https://github.com/Knighthood2001/u_shaped_gimbal
  上面这个，我目前只是仿真了这个云台，以及控制这个云台进行运动，但是，目前还没有搭载仿真雷达，后续应该会完善。

• 这两个GitHub链接的话，上面这个，由于只是结构仿真，自由度高，你能够仿真出两个轴不平行的情况，来验证一些设备上的误差导致算法的结果产生偏移。