考古并发历史（1）

并发问题之前先有竞态。最早竞态问题只是被描述为一种争夺资源的过程。而在Dekker提出了临界区的概念本质上又依赖于一个循环的概念进行描述。

Dekker 算法（1959）

// P0 的伪代码
int turn   //记录轮数避免死锁
flag[0] = true;  //标志位
while (flag[1]) {           // 如果 P1 也想进入if (turn != 0) {        // 轮到 P1？
        flag[0] = false;    // 让 P1 优先while (turn != 0) ; // 等待轮到自己
        flag[0] = true;     // 再次尝试进入}
}
// 临界区
critical_section();
// 离开临界区
turn = 1;
flag[0] = false;

Solution of a Problem in Concurrent Programming Control （Dijkstra ）（1965 ）

integer j;  // 定义整型变量 j，用于循环计数LiO: 
    b[i] := false;  // 标签 LiO：进程 i 开始循环，标记自己暂时不进入临界区Lil: if k # i then  // 如果轮到的进程 k 不是自己，则进入以下逻辑
Li2: 
        begin
            c[i] := true;  // 标记进程 i 已准备好进入临界区
Li3: if b[k] then k := i;  // 如果进程 k 想进入临界区，则将轮次指向自己
            go to Lil;             // 回到 Lil 标签，重新检查顺序
        endelse
Li4: 
        begin
            c[i] := false;  // 否则（轮到自己），暂时取消准备状态for j := 1 step 1 until N do  // 检查所有进程 j（1..N）if j # i and not c[j] then go to Lil; // 如果 j 不是自己且未准备好，回到 Lil 重新检查
        end;    critical section; // 临界区：执行需要互斥访问的操作    c[i] := true; // 临界区结束后，标记自己完成访问
    b[i] := true; // 标记自己允许其他进程检查/轮到自己    remainder of the cycle in which stopping is allowed;  // 临界区之外的操作，可以被中断或调度    go to LiO;  // 回到 LiO 标签，进入下一轮循环

首先我们要注意这个版本的Dijkstra提出的算法他自己也强调了两个前提即对称和循环。然后这篇论文除了将并发问题扩展到n个进程。还引申出了一个概念---顺序。为什么需要顺序呢？引入顺序，使每个进程在尝试进入临界区时按照固定顺序检查前面的进程且保证一次只有一个进程可以进入临界区。顺序即是一个唯一标识起到区分的作用。同时也是一种等待凭证....

然后还有就是当时这个算法的提出是没有考虑死锁检查的或者说这个假设的场景太过于理想。依赖于一个轮次的检查来保证不发生同时进入等待状态。而这个维护轮次的变量是安全的吗？在后现代的一些理论也意识到在多核cpu中这个过程也是不可靠的......

事实上关于顺序和一些离散的描述Dijkstra在 Cooperating sequential processes 提出过更加完整的模型和解释

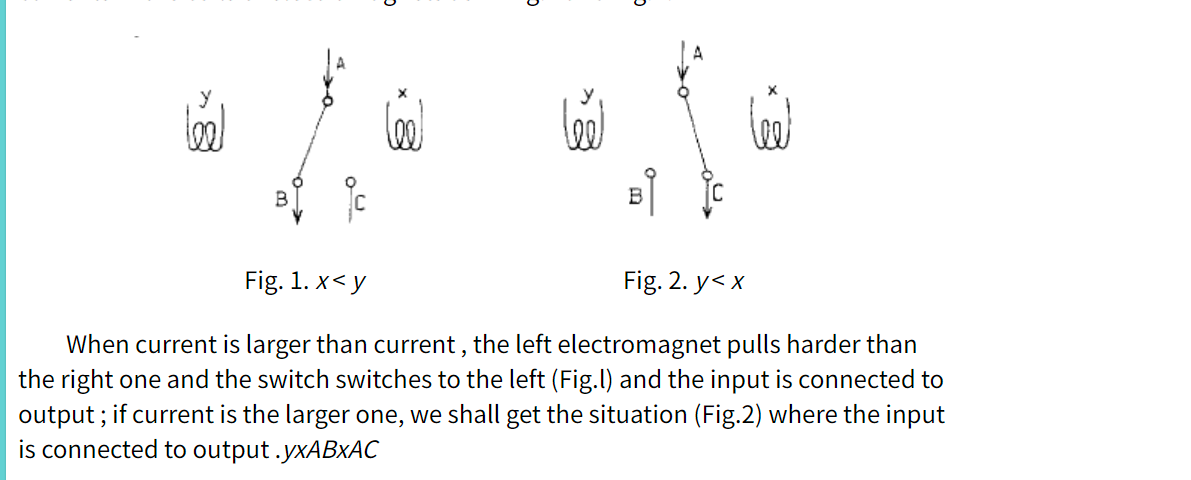
参考这段描述 描述这种设备是一种非顺序的设备原因在于这里同时输入电流所构造出来的结果总会得到最终的一致性

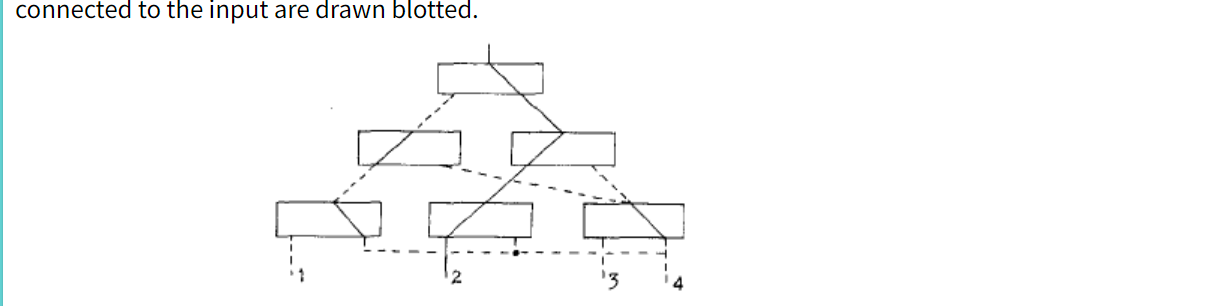
然后大概一直迭代

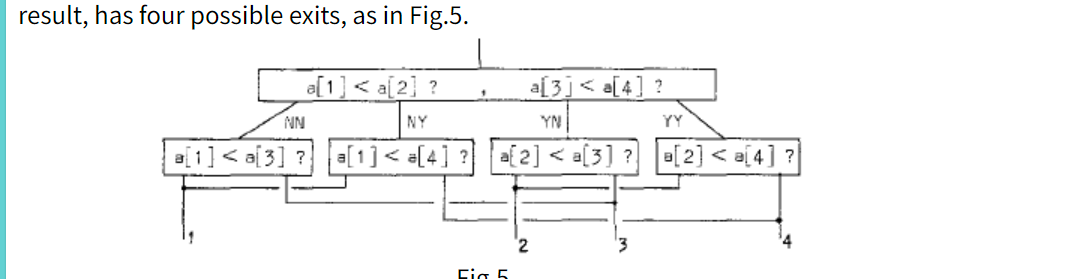
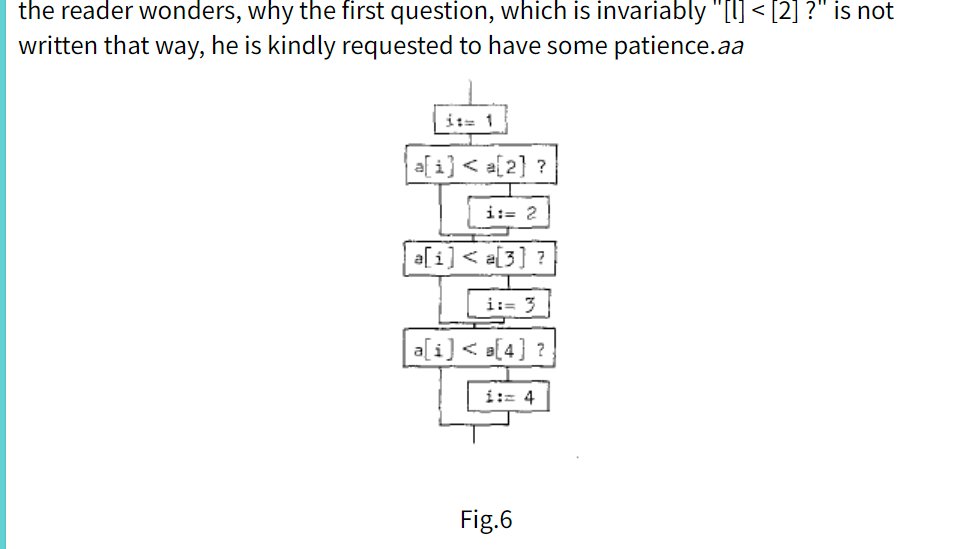
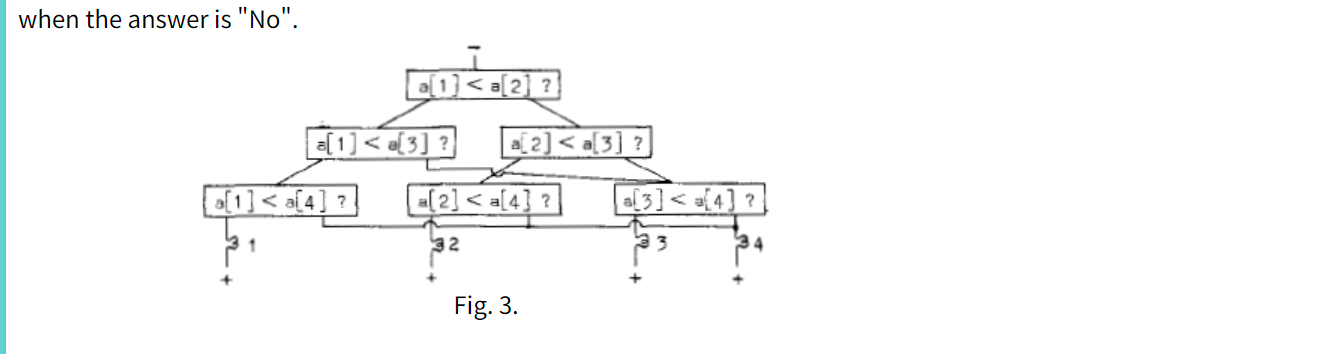
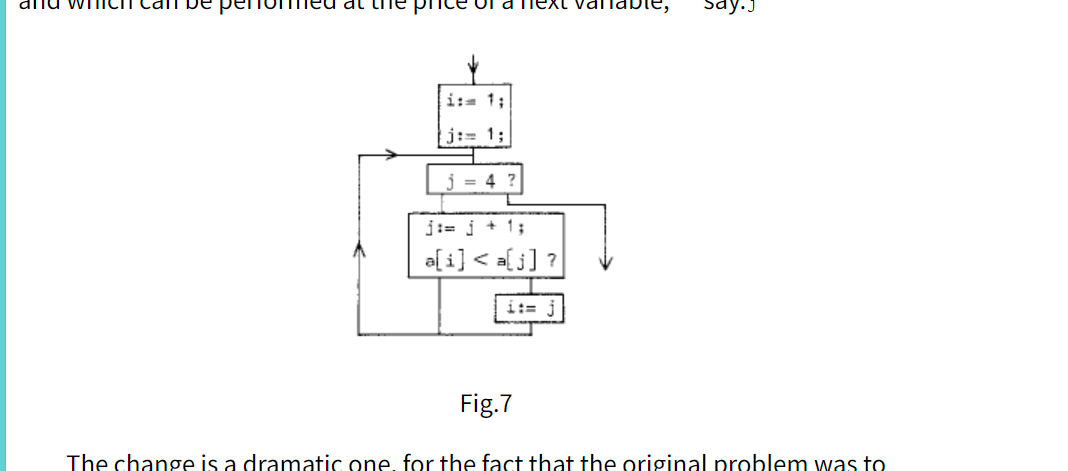他假设了机械的几种迭代方式来说明一种抽象的概念的即---顺序和非顺序机械的区别和互相转换的点的。

题主这边总结了两个点并提供了对应的连接。要明确的是这个时候计算机并发理论还没有引入如因果和偏序这样的概念。所以还请各位看主仔细审视。学习如果为了做题可以拿着一个结论应付先行，但奥妙之处往往在于学习的再发现。

在非顺序机器中，比较事件之间不可比；

在顺序机器中，比较事件之间全序（total order）；

在非顺序中我们判断的标准不是具体的运算。而是依赖于如同机械结构传导这样的东西。也就是所谓的不可比性。更深刻的来说是这种类似于最终一致性。我们怎么判断怎么样是最终？而什么样是达到稳定的。

而在全序比较中就是强调一种运算上的可比性。所以对于状态的判断取决于这种运算上的可比性来锚定。

E.W.Dijkstra Archive: Cooperating sequential processes (EWD 123) (utexas.edu)