【C++】前缀和算法习题

🎆个人主页：夜晚中的人海

今日语录：谁和我一样用功，谁就会和我一样成功。 —— 莫扎特

⭐一、【模板】前缀和

题目链接：【模板】前缀和

题目描述：

解题思路：
1.根据题目要求，我们可以先预处理出一个前缀和的数组

2.dp[i]表示[l , i]区间内所有元素的和，dp[i - 1]表示[l , i - 1]区间内所有区间内的和；因此我们可以得到一个递推公式：dp[i] = dp[i - 1] + arr[i]

3.因此我们可以使用前缀和数组快速求出某一段区间内的和，从而解决问题

代码实现：

#include <iostream>
using namespace std;const int N = 100000;
long long arr[N],dp[N];int main() 
{int n = 0,m = 0;cin >> n >> m;for(int i = 1;i <= n;i++){cin >> arr[i];}for(int j = 1;j <= n;j++){//列举每一位的前缀和dp[j] = dp[j - 1] + arr[j];}while(m--){int l = 0,r = 0;cin >> l >> r;cout << dp[r] - dp[l - 1] << endl;}return 0;
}

🎄二、【模板】二维前缀和

题目链接：【模板】二维前缀和

题目描述：

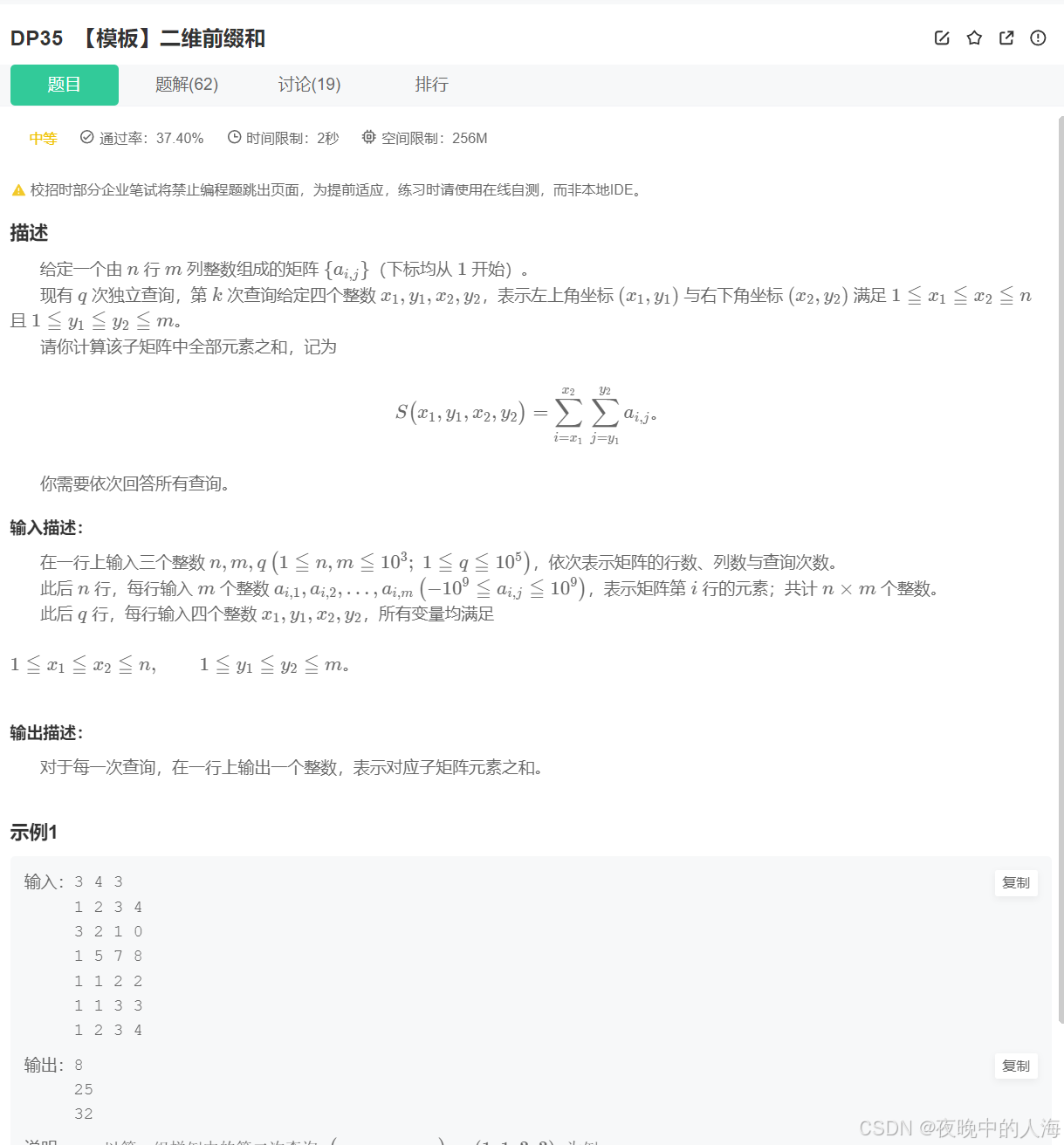
解题思路：
1.我们还是向一维数组的方式一样搞出来一个前缀和数组，但在处理二维数组中的边界时有许多条件需要处理，因此我们要在矩阵的最上面和最左边添加上一行和⼀列0，处理结果如下图所示

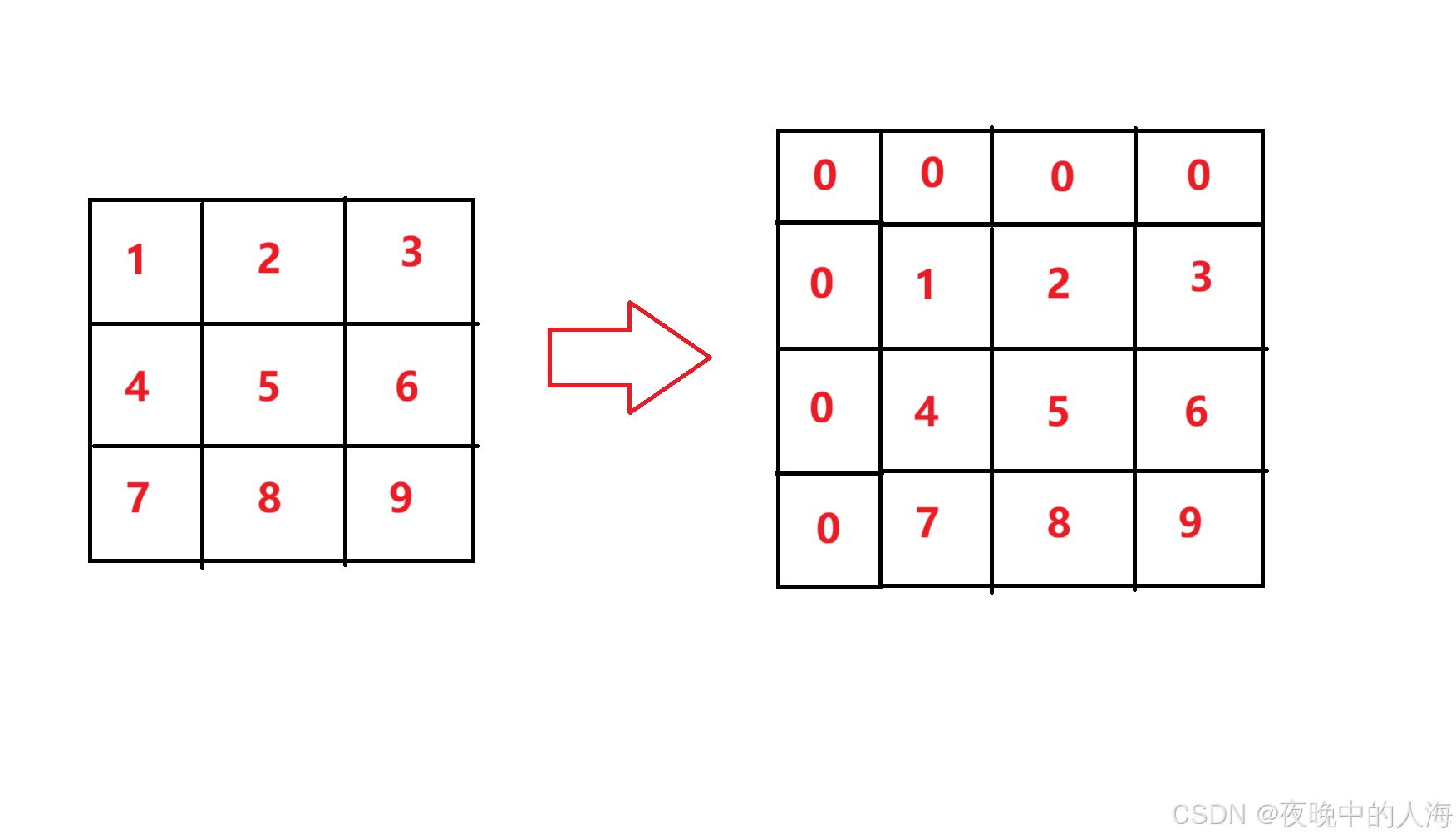
2.处理完成后，我们在使用前缀和数组时，下标从1开始，就可以大胆使用 i - 1，j - 1位的值了
（注： 由于我们添加了一行和一列的值，在原数组和前缀和数组中，它们的映射关系就发生了变化：从前缀和数组中到原数组，横纵坐标 - 1，从数组到前缀和数组中，横纵坐标 + 1）

3.我们使用sum[ i ][ j ]来表示从[ 0 ][ 0 ] 到 [ i ][ j ]这一区间内所有元素的和，如下图所示：

4.我们可以将[ 0 ][ 0 ]位置到[ i ][ j ]位置分成四段区域如下图所示：

在求解蓝色区域时非常好求，它就是数组中arr[i - 1][j - 1]的位置
在单独求解黄色区域以及绿色区域时不太好求，但如果是红+黄以及红+ 绿这段区域时，那就非常好求了，求出来的三个值累加起来，那就是红 + 黄 + 红 + 绿 + 蓝，我们发现多加了一次红，把红色这块区域减掉一次即可

5.求出上述的前缀和矩阵，我们就可以来使用该矩阵，在使用该矩阵时，我们要注意让每个下标都++，这样才能映射到前缀和矩阵中

6.根据上图所示，我们要想求蓝色区域的面积，就来分析一下其它几块区域
• 我们可以快速求出整块区域的面积，就是sum[row2][col2],用整块面积去减去其它区域的面积，单独求绿色区域以及黄色区域的面积不太好求，但如果求红 + 黄以及红 + 绿这片区域那就很好求了：红 + 黄：sum[row1 - 1][col2] 红+ 绿：[row2][co1 - 1],由于我们多减了一次红色区域，因此要加上一次红色区域的面积：arr[row1 - 1][col1 - 1]，根据上述操作，这样求出来我们所需要蓝色区域的面积了

代码实现：

#include <iostream>
#include<vector>
using namespace std;int main() 
{int n = 0,m = 0,q = 0;cin>>n>>m>>q;vector<vector<int>> arr(n + 1,vector<int>(m + 1));for(int i = 1;i <= n;i++){for(int j = 1;j <= m;j++){cin>> arr[i][j];}}//预处理前缀和数组vector<vector<long long>> dp(n + 1,vector<long long>(m + 1));for(int i = 1;i <= n;i++){for(int j = 1;j <= m;j++){dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + arr[i][j] - dp[i - 1][j - 1];}}//使用前缀和数组while(q--){int x1 = 0,x2 = 0,y1 = 0,y2 = 0;cin>>x1>>y1>>x2>>y2;cout<<dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1-1]<<endl;}
}

🎆三、寻找数组的中心下标

题目链接：寻找数组的中心下标

题目描述：

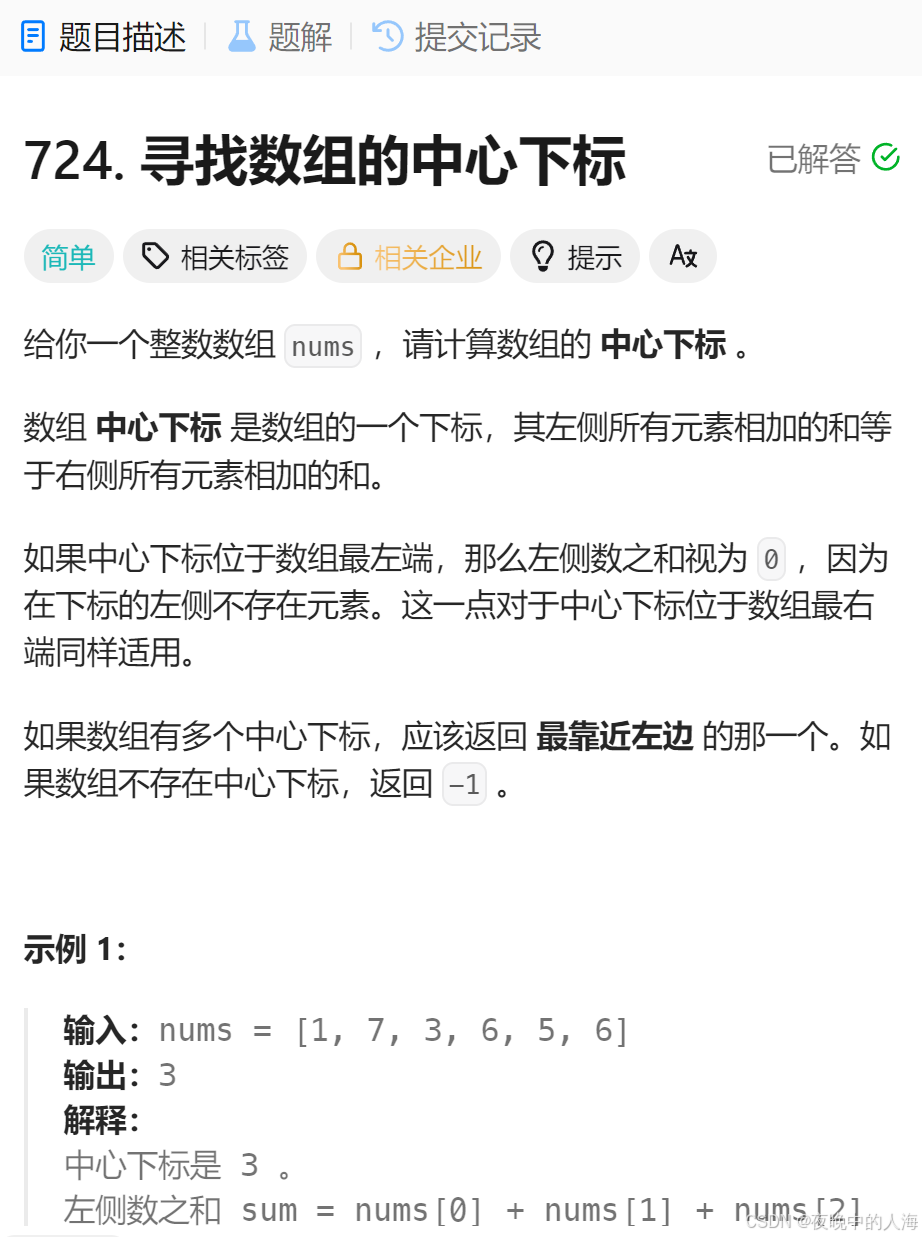
解题思路：
1.定义两个数组，一个表示前缀和，另一个表示后缀和

2.用一个for循环枚举每一个可能是中心点的下标，如果该下标的前缀和和后缀和都相等，则返回；循环结束后若还是没找到，则返回-1

代码实现：

class Solution {
public:int pivotIndex(vector<int>& nums) {int n = nums.size();vector<int> f(n),g(n);//计算前缀和for(int i = 1;i < n;i++){f[i] = f[i - 1] + nums[i - 1];}//计算后缀和for(int j = n - 2;j >= 0;j--){g[j] = g[j + 1] + nums[j + 1];}for(int i = 0;i < n;i++){if(f[i] == g[i])return i;}return -1;}
};

🚀四、除自身以外数组的乘积

题目链接：除自身以外数组的乘积

题目描述：

解题思路：
1.跟前缀和思路算法类型，定义两个数组，一个表示前缀和的乘积，另一个表示后缀和的乘积

2.遍历一次数组，根据题目要求返回结果即可

代码实现：

class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {int n = nums.size();vector<int> f(n),g(n),answer(n);f[0] = 1,g[n - 1] = 1;//前缀乘积for(int i = 1;i < n;i++){f[i] = f[i - 1] * nums[i - 1];}//后缀乘积for(int j = n - 2;j >= 0;j--){g[j] = g[j + 1] * nums[j + 1];}//结果for(int i = 0;i < n;i++){answer[i] = f[i] * g[i];}return answer;}
};

🚘五、和可被K整除的子数组

题目链接：和可被K整除的子数组

题目描述：

解题思路：
1.在解决此类问题时，我们需要补充两个知识点：
同余定理： 如果(a - b) % n == 0 ，那么我们可以得到⼀个结论： a % n == b % n
负数取模： 为了避免出现负数的结果，我们以(a % n + n) % n 的形式来确保结果是正数

2.根据上述的补充，我们就只需要求出有多少个前缀和的余数等于sum % k即可，使用⼀个哈希表，一边求当前位置的前缀和，⼀边存下之前每⼀种前缀和出现的次数

代码实现：

class Solution {
public:int subarraysDivByK(vector<int>& nums, int k) {int n = nums.size();unordered_map<int,int> hash;//处理特殊情况hash[0 % k] = 1;int sum = 0,ret = 0;for(auto x : nums){sum += x;int r = (sum % k + k) % k;if(hash.count(r))ret += hash[r];hash[r]++;}return ret;}
};

🏝️六、连续数组

题目链接：连续数组

题目描述：

解题思路：
1.题目要求我们要找具有相同数量的0和1，我们可以转变一下思路，将0转变成-1，从而改变寻找一段区间和为0的区域

2.使用哈希表记录当前位置的前缀和以及第一次出现该前缀和的位置

代码实现：

class Solution {
public:int findMaxLength(vector<int>& nums) {int n = nums.size();unordered_map<int,int> hash;hash[0] = -1;int sum = 0,ret = 0;for(int i = 0;i < n;i++){sum += nums[i] == 0 ? -1 : 1;if(hash.count(sum))ret = max(ret,i - hash[sum]);elsehash[sum] = i;}return ret;}
};

🏖️七、矩阵区域和

题目链接：矩阵区域和

题目描述：

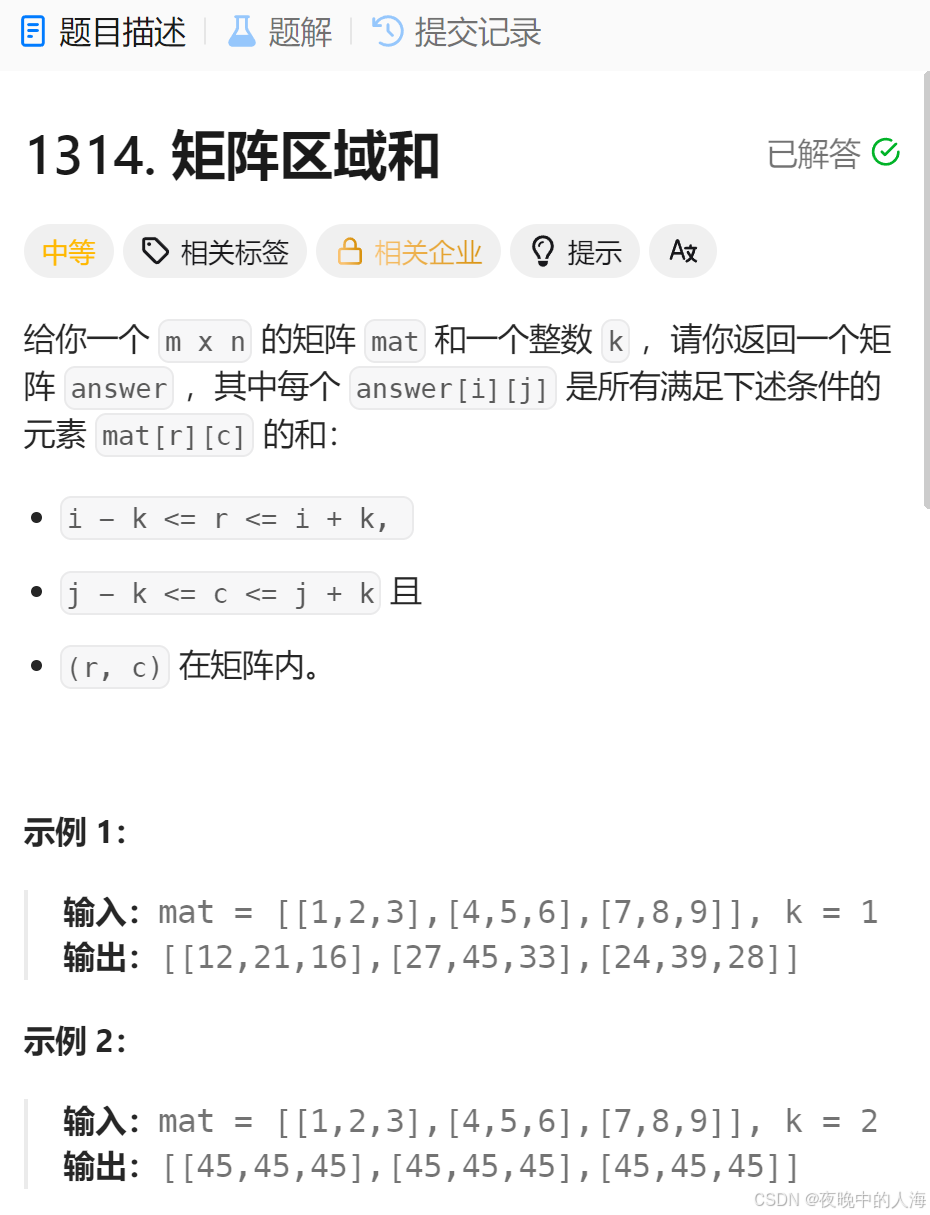
解题思路：
1.使用两个数组，一个用来预处理前缀和的数组，另一个作为返回结果的数组

2.根据前面二维矩阵的相关解法，最需要注意的就是两数组的映射关系问题，弄清楚它们之间的映射关系，我们就可以快速的解决此类问题

代码实现：

class Solution {
public:vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {int m = mat.size();int n = mat[0].size();vector<vector<int>> dp(m + 1,vector<int>(n + 1));//预处理前缀和数组for(int i = 1;i <= m;i++){for(int j = 1;j <= n;j++){dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1]+ mat[i - 1][j - 1];}}//使用前缀和数组vector<vector<int>> answer(m,vector<int>(n));for(int i = 0;i < m;i++){for(int j = 0;j < n;j++){//防止超越矩阵的范围int x1 = max(0,i - k) + 1,y1 = max(0,j - k) + 1;int x2 = min(m - 1,i + k) + 1,y2 = min(n - 1,j + k) + 1;answer[i][j] = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1];}}return answer;}
};