LeetCode 1901.寻找峰值2

一个 2D 网格中的 峰值 是指那些 严格大于 其相邻格子(上、下、左、右)的元素。

给你一个 从 0 开始编号 的 m x n 矩阵 mat ，其中任意两个相邻格子的值都 不相同 。找出 任意一个 峰值 mat[i][j] 并 返回其位置 [i,j] 。

你可以假设整个矩阵周边环绕着一圈值为 -1 的格子。

要求必须写出时间复杂度为 O(m log(n)) 或 O(n log(m)) 的算法

示例 1:

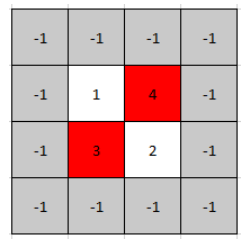
输入: mat = [[1,4],[3,2]]
输出: [0,1]
解释: 3 和 4 都是峰值，所以[1,0]和[0,1]都是可接受的答案。
示例 2:

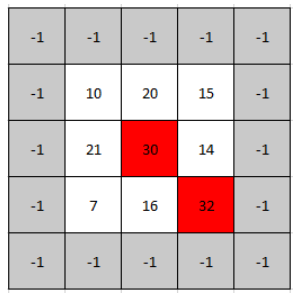
输入: mat = [[10,20,15],[21,30,14],[7,16,32]]
输出: [1,1]
解释: 30 和 32 都是峰值，所以[1,1]和[2,2]都是可接受的答案。

提示：

m == mat.length
n == mat[i].length
1 <= m, n <= 500
1 <= mat[i][j] <= 10${}^5$
任意两个相邻元素均不相等.

如何找到一个山顶？我们可以从某个点出发，一直往四周最大的那个格子移动，那么最终一定会到达山顶。因此我们可以对行进行二分，如果当前二分到的行中的最大值比上下相邻格子的值都大，那么它就是一个山顶，否则往大值的方向继续二分即可：

class Solution {
public:vector<int> findPeakGrid(vector<vector<int>>& mat) {int rowNum = mat.size();int colNum = mat[0].size();int l = 0;int r = rowNum - 1;while (l <= r) {int m = l + (r - l) / 2;int maxIdx = max_element(mat[m].begin(), mat[m].end()) - mat[m].begin();if ((m == 0 || mat[m - 1][maxIdx] < mat[m][maxIdx]) && (m == rowNum - 1 || mat[m + 1][maxIdx] < mat[m][maxIdx])) {return {m, maxIdx};} else if (mat[m + 1][maxIdx] > mat[m][maxIdx]) {l = m + 1;} else {r = m - 1;}}return {-1, -1};}
};

如果mat有m行n列，则此算法时间复杂度为O(nlogm)，空间复杂度为O(1)。