逻辑回归解释
一、介绍：
逻辑回归主要是二分类的算法，给定一组（x1、x2...）输出该样本预测类别结果为1的概率值：y=P(y=1|x)。
二、原理：
z=w1x1+w2x2+...wnxn+b
1、x1、x2...是输入的特征
2、w1、w2...是模型学习到的每个特征的权重
3、b是偏置，模型学习的
4、z是计算结果，属于（-∞，+∞）
然后是sigmoid函数部分
由于z属于（-∞，+∞），输出的不是离散的1和0，所以使用sigmoid函数把z压缩到（0，1）之间。
公式：y = 1 / (1 + e^(-z))
性质：
无论
z是多少，y的输出值永远在 0 和 1 之间。当
z为 0 时，y = 0.5。当
z非常大时，y无限接近 1。当
z非常小时，y无限接近 0。
例子：
假设我们构建一个更完善的河流洪水预测模型，现在使用三个特征：
X₁: 过去24小时流域降雨量 (mm)
X₂: 河流上游监测站的水位 (m)
X₃: 土壤饱和指数 (0-1之间，1表示完全饱和)
第一步：训练好的模型
假设模型训练后，学到的参数如下：
权重 W₁ (降雨量): 0.08
权重 W₂ (水位): 1.5
权重 W₃ (土壤饱和度): 4.0
偏置项 b: -10
线性组合 z 的公式为：
z = (0.08 * X₁) + (1.5 * X₂) + (4.0 * X₃) - 10
概率 P 的公式（Sigmoid函数）不变：
P(洪水) = 1 / (1 + e^(-z))
这个模型可以理解为：
土壤饱和度 (X₃) 的权重最大 (4.0)，说明它是引发洪水的最关键因素。因为已经饱和的土壤无法再下渗，雨水会直接转化为径流。
水位 (X₂) 的权重也很大 (1.5)，表示当前河道的底水情况非常重要。
降雨量 (X₁) 的权重相对较小 (0.08)，但这不代表它不重要，只是因为它的数值通常远大于其他特征（比如降雨量是几十，水位是几，土壤饱和度是零点几）。
第二步：多场景分类决策（阈值仍设为0.5）
现在我们分析三种不同的气象水文组合。
场景一：台风过境，强降雨但底水低
X₁ (降雨量): 120 mm （很大）
X₂ (水位): 1.2 m （较低）
X₃ (土壤饱和度): 0.4 （因为前期干旱，土壤较干）
计算 z:
z = (0.08 * 120) + (1.5 * 1.2) + (4.0 * 0.4) - 10z = 9.6 + 1.8 + 1.6 - 10 = 3.0计算 P:
P = 1 / (1 + e^(-3.0)) ≈ 1 / (1 + 0.05) ≈ 0.95决策:
P = 0.95 > 0.5→ 预测：发生洪水 (1)
解读：尽管初始水位低、土壤不算饱和，但极端降雨量本身足以导致洪水。
场景二：持续阴雨，高水位且土壤饱和
X₁ (降雨量): 25 mm （小雨）
X₂ (水位): 3.0 m （已接近警戒水位）
X₃ (土壤饱和度): 0.95 （土壤已经完全饱和）
计算 z:
z = (0.08 * 25) + (1.5 * 3.0) + (4.0 * 0.95) - 10z = 2.0 + 4.5 + 3.8 - 10 = 0.3计算 P:
P = 1 / (1 + e^(-0.3)) ≈ 1 / (1 + 0.74) ≈ 0.57决策:
P = 0.57 > 0.5→ 预测：发生洪水 (1)
解读：这就是典型的“最后一根稻草” scenario。虽然雨不大，但河道底水高，加上土壤饱和，即使是少量降雨也会几乎全部汇入河道，导致水位超过临界点。
场景三：普通降雨，各项指标正常
X₁ (降雨量): 15 mm
X₂ (水位): 1.5 m
X₃ (土壤饱和度): 0.6
计算 z:
z = (0.08 * 15) + (1.5 * 1.5) + (4.0 * 0.6) - 10z = 1.2 + 2.25 + 2.4 - 10 = -4.15计算 P:
P = 1 / (1 + e^(-(-4.15)))) ≈ 1 / (1 + 63.5) ≈ 0.015决策:
P = 0.015 < 0.5→ 预测：不发生洪水 (0)
解读：所有指标都在安全范围内，系统综合判断风险极低。
第三步：引入更精细的决策阈值（多级预警）
在实际水文预警中，单一的“是/否”决策太粗糙了。我们会使用多个阈值来建立多级预警系统，这更能体现逻辑回归输出概率的优势。
蓝色预警 (关注级):
P >= 0.3通知水务部门和相关人员保持警惕，加强监测。
黄色预警 (警示级):
P >= 0.6向公众发布预警信息，提醒远离河道。
橙色预警 (行动级):
P >= 0.8启动应急响应预案，准备疏散低洼地区人员。
红色预警 (紧急级):
P >= 0.95立即执行疏散命令，采取一切必要措施。
现在，我们用这个多级预警系统重新审视上面的场景：
场景一 (P=0.95): 直接触发红色预警。模型非常有把握，需要立即采取最高级别的应急行动。
场景二 (P=0.57): 触发黄色预警。模型认为风险显著，需要提醒公众注意，但尚未达到需要大规模疏散的程度。
场景三 (P=0.015): 无预警。一切正常
三、逻辑回归的损失函数
平方差损失函数：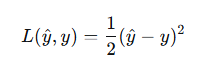
不适用--产生多个局部最小值
这里的损失函数：
如果 y=1，损失为 -log(ŷ)，那么要想损失越小，ŷ 的值必须越大，即越趋近于或者等于 1
如果 y=0，损失为 -log(1-ŷ)，那么要想损失越小，那么 ŷ 的值越小，即趋近于或者等于 0
这个损失函数关注单个样本的预测误差
而多个样本的预测误差的算数平均为代价函数：
四、梯度下降
通过损失函数找到了预测值与目标值之间的误差，那么我们怎么优化呢，找到最合适的参数配置使损失达到最低。因此这里需要使用梯度下降算法：使损失函数达到最小值。
参数w和b的更新公式：
