MATLAB图形绘制基础（一）二维图形

MATLAB可以绘制二维、三维及多维图形（人类视觉系统只能感知三维空间），除了能在直角坐标系下绘图，也能在极坐标、对数坐标系下绘图，并且还能对图形加以修饰。

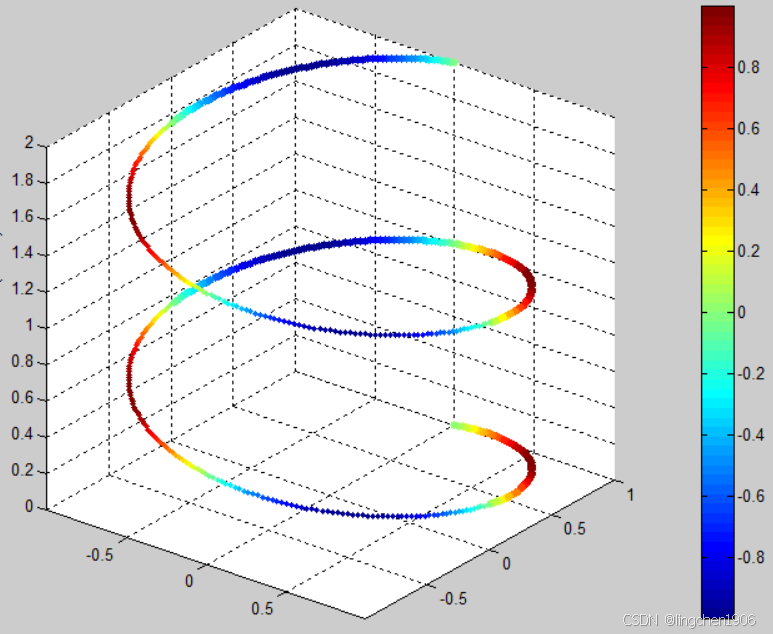
人类视觉系统只能感知三维空间，但可以通过维度映射将 5 个维度的信息通过 “三维空间坐标 + 两个视觉属性（如颜色、大小）” 来模拟可视化。

1. 维度映射逻辑：

   • 前 3 个维度：直接对应三维空间坐标（x,y,z），构成 “基础空间”；
   • 第 4 个维度：通过点的颜色（颜色条对应数值大小）体现；
   • 第 5 个维度：通过点的尺寸（数值越大，点越大）体现。

2. 核心思路：
   由于物理空间仅三维，高维空间的可视化本质是 “将额外维度编码为人类可感知的视觉属性”（颜色、大小、形状等）。这种方法在数据分析中广泛用于观察高维数据的内在关联（例如，颜色与大小的变化是否同步，是否与空间坐标存在规律）。

（1）、二维图形绘制（含多坐标系）

MATLAB 2010b 提供了丰富的二维绘图函数，覆盖不同坐标系需求：

1. 直角坐标系（最基础）

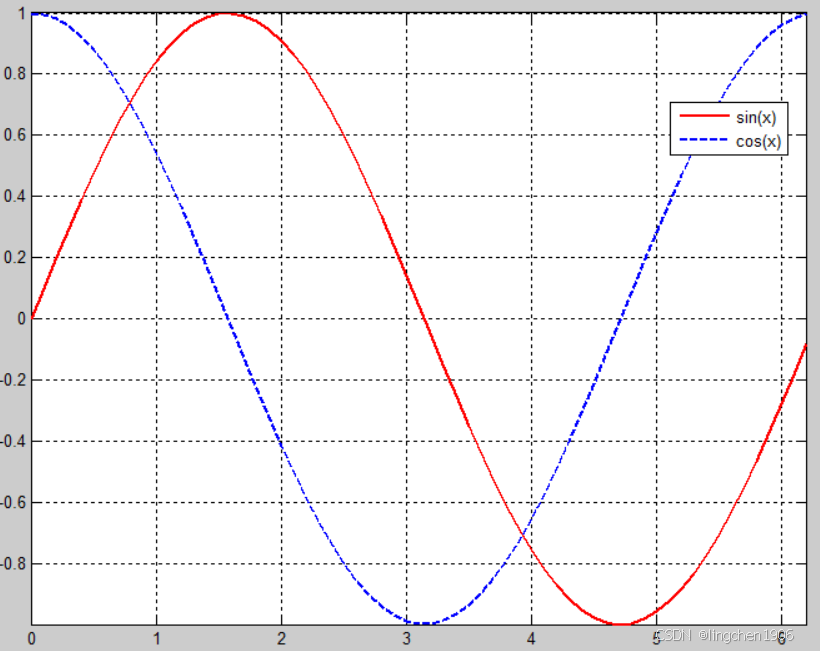
核心函数为plot，用于绘制平面曲线，支持单条或多条曲线叠加。示例：绘制正弦曲线并叠加余弦曲线

x = 0:0.1:2*pi;  % x范围：0到2π，步长0.1
y1 = sin(x);     % 正弦函数
y2 = cos(x);     % 余弦函数
plot(x, y1, 'r-', x, y2, 'b--');  % 红色实线正弦，蓝色虚线余弦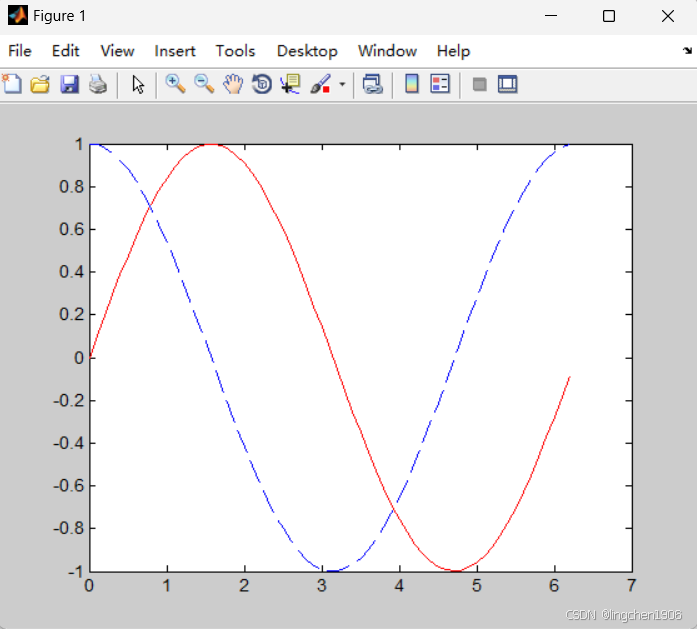

2. 极坐标系

通过polar函数实现极坐标图形绘制，输入参数为极角theta（弧度）和极径rho。示例：绘制极坐标下的花瓣曲线（ρ=sin (2θ) cos (2θ)）

theta = 0:0.01:2*pi;  % 极角范围
rho = sin(2*theta) .* cos(2*theta);  % 极径
polar(theta, rho, 'g-');  % 绿色实线绘制极坐标曲线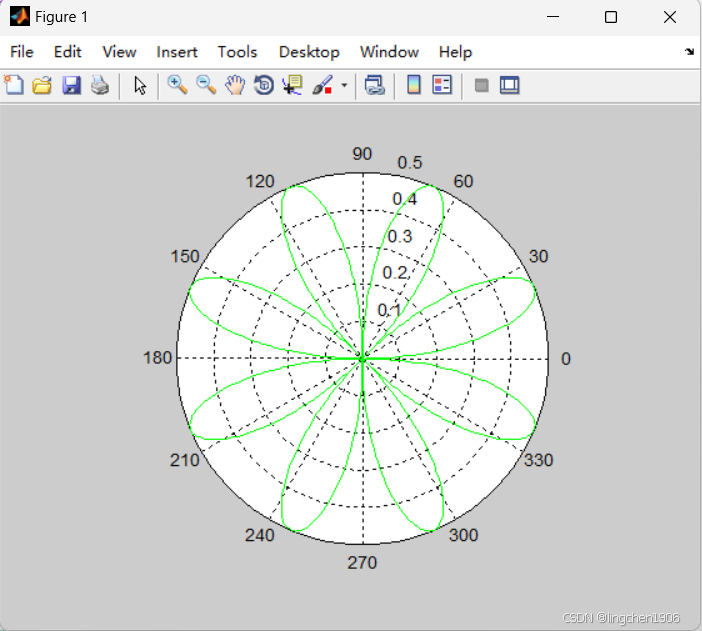

3. 对数坐标系

针对数据范围跨度大的场景，提供三种对数坐标函数：

• semilogx：x 轴为对数刻度，y 轴为线性刻度；
• semilogy：y 轴为对数刻度，x 轴为线性刻度；
• loglog：x、y 轴均为对数刻度。

示例1：用双对数坐标绘制幂函数 y=x²

x = 1:100;  % x范围1到100
y = x .^ 2;  % 幂函数
loglog(x, y, 'm*');  % 双对数坐标，紫色星号标记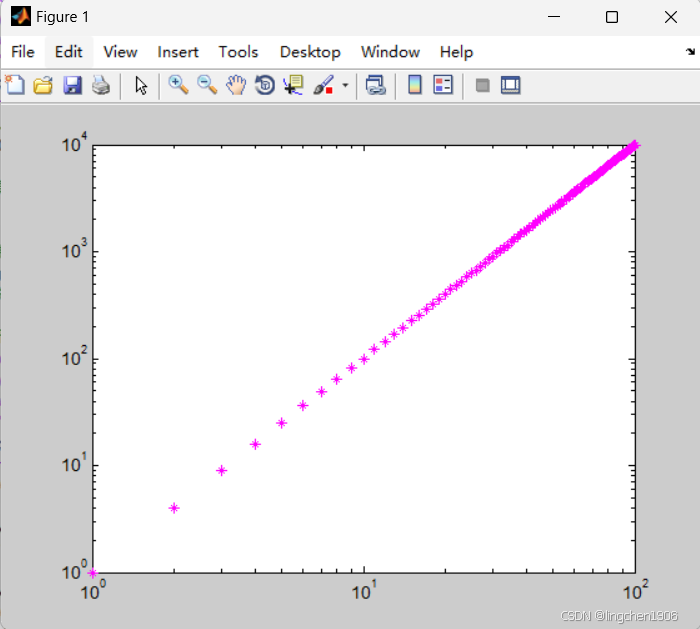

示例2：用x 轴为对数刻度，y 轴为线性刻度坐标绘制幂函数 y=x²

% 1. 定义x的范围（x>0，覆盖0.1到100，包含多个数量级）
x = 0.1:0.05:100;  % 步长0.05，保证曲线平滑% 2. 计算幂函数 y = x² 的值（向量运算需用 .^）
y = x .^ 2;% 3. 绘制图形（x轴对数刻度，y轴线性刻度）
semilogx(x, y, 'r-', 'Marker', 'o', 'MarkerSize', 3, 'LineWidth', 1.2);  
% 参数说明：红色实线，圆圈标记点，标记大小3，线宽1.2% 4. 图形修饰（2010b支持所有以下函数）
xlabel('x (Logarithmic scale)');       % x轴标签，注明刻度类型
ylabel('y (Linear scale) ');       % y轴标签，注明刻度类型
title('Power function y = x^2  (x-axis logarithmic, y-axis linear) ');  % 图形标题
legend('y = x^2');             % 标注曲线含义
grid on;                       % 显示网格（对数刻度下更易观察趋势）
axis tight;                    % 坐标轴范围自适应数据范围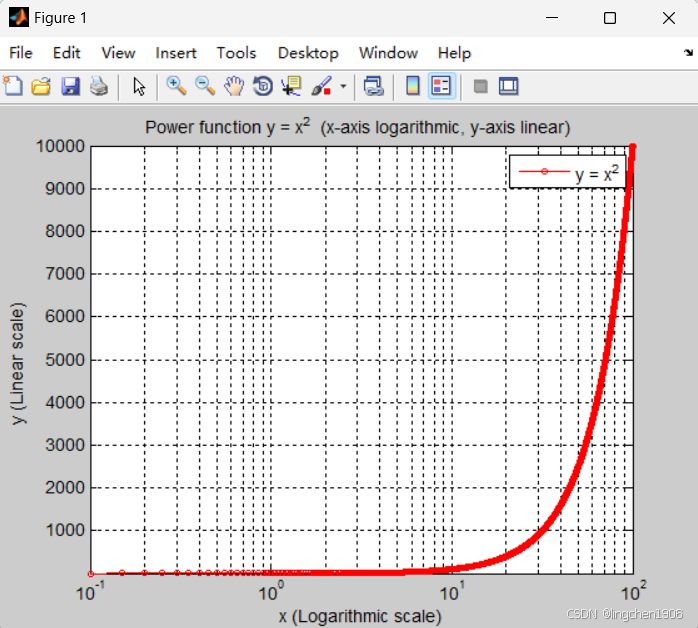

结果说明（MATLAB 2010b 中运行）

• 坐标轴特性：x 轴为对数刻度（刻度值按 \(10^0, 10^1, 10^2\) 等分布，即 1、10、100），适合展示 x 跨越多个数量级的场景；y 轴为线性刻度，直接反映 \(y = x^2\) 的数值大小。
• 图形意义：\(y = x^2\) 在 x 轴对数刻度下呈现为直线（因对数变换后 \(\log y = 2\log x\)，为线性关系），清晰体现 “x 每扩大 10 倍，y 扩大 100 倍” 的平方增长规律（比线性 x 轴更直观）。

注意事项（针对 2010b 版本）

• 若需调整 x 的范围，直接修改 x = 0.1:0.05:100; 中的起始值、步长或结束值即可（确保 x>0）；
• 2010b 中 semilogx 函数的属性设置（如 Marker、LineWidth）与高版本兼容，无需修改语法；
• 若图形中出现警告，通常是因 x 接近 0 导致（但此处 x 起始为 0.1，可避免）。

示例3：用y 轴为对数刻度，x轴为线性刻度坐标绘制幂函数 y=x²

% 1. 定义x的范围（x为线性刻度，包含正负值，覆盖-10到10）
x = 0.1:0.05:100;  % 步长0.05，保证曲线平滑% 2. 计算幂函数 y = x² 的值（向量运算需用 .^ 对每个元素求平方）
y = x .^ 2;% 3. 绘制图形（y轴对数刻度，x轴线性刻度）
semilogy(x, y, 'b-', 'Marker', 'o', 'MarkerSize', 3, 'LineWidth', 1.2);  
% 参数说明：蓝色实线，圆圈标记点，标记大小3，线宽1.2% 4. 图形修饰（2010b支持所有以下函数）
xlabel('x (Logarithmic scale)');       % x轴标签，注明刻度类型
ylabel('y (Linear scale)');       % y轴标签，注明刻度类型
title('Power function y = x^2 (x-axis logarithmic, y-axis linear)');  % 图形标题
legend('y = x^2');             % 标注曲线含义
grid on;                       % 显示网格（对数刻度下更易观察趋势）
axis tight;                    % 坐标轴范围自适应数据范围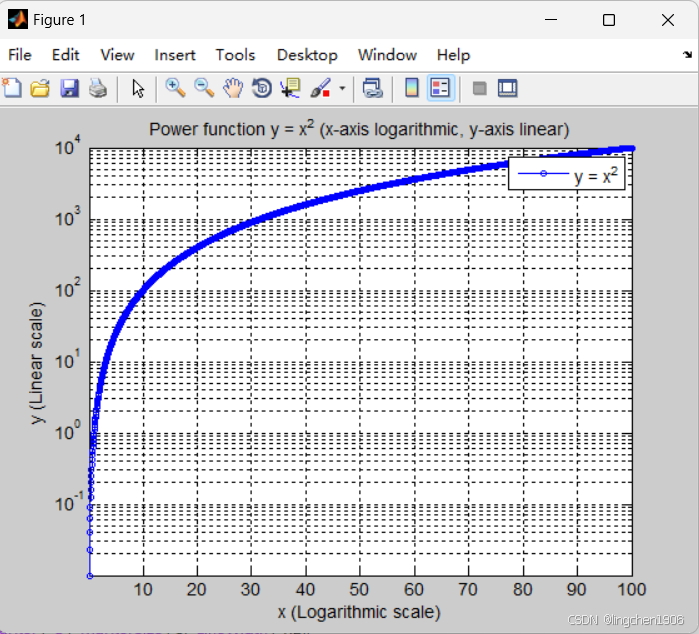

结果说明（MATLAB 2010b 中运行）

• 坐标轴特性：x 轴为线性刻度（均匀分布从 - 10 到 10），直观展示 x 的正负对称特性；y 轴为对数刻度（刻度值按 \(10^k\) 分布，如 1、10、100 等），适合展示 \(y = x^2\) 随 x 绝对值增大而快速增长的趋势（避免线性 y 轴下 “大值区域曲线重叠” 的问题）。
• 图形意义：\(y = x^2\) 是偶函数，图形关于 y 轴对称；在 y 轴对数刻度下，x 绝对值越大（如 | x|=1, 10），y 值（1, 100）在对数轴上呈现线性增长趋势（因 \(\log y = 2\log|x|\)，为线性关系），清晰体现平方增长的速率。

注意事项（针对 2010b 版本）

• 若需调整 x 的范围（如扩大到 - 20 到 20），直接修改 x = -10:0.1:10; 中的起始值或结束值即可（x 可正可负，因 y 恒为正）；
• 2010b 中 semilogy 函数的属性设置（如 Marker、LineWidth）与高版本兼容，无需修改语法；
• 因 \(y = x^2\) 恒为非负（且仅 x=0 时 y=0），而对数刻度不支持 0，代码中 x=0 时 y=0 会在图形中显示为接近 0 的点（不影响整体趋势）。

（2）、三维图形绘制

MATLAB 2010b 支持三维曲线、曲面等图形，核心函数如下：

1. 三维曲线

通过plot3函数绘制，需输入 x、y、z 三个维度的坐标。示例：绘制三维螺旋线

t = 0:0.1:10*pi;  % 参数t
x = sin(t);       % x坐标
y = cos(t);       % y坐标
z = t;            % z坐标（沿z轴延伸）
plot3(x, y, z, 'k-');  % 黑色实线绘制螺旋线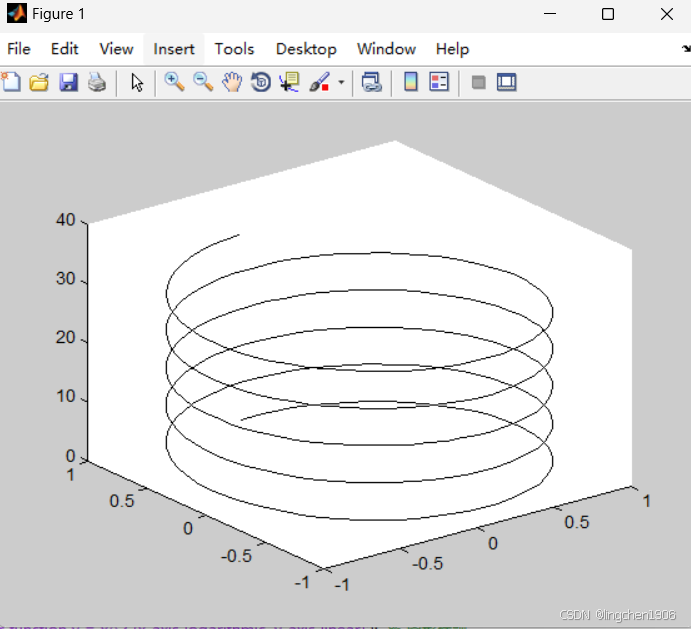

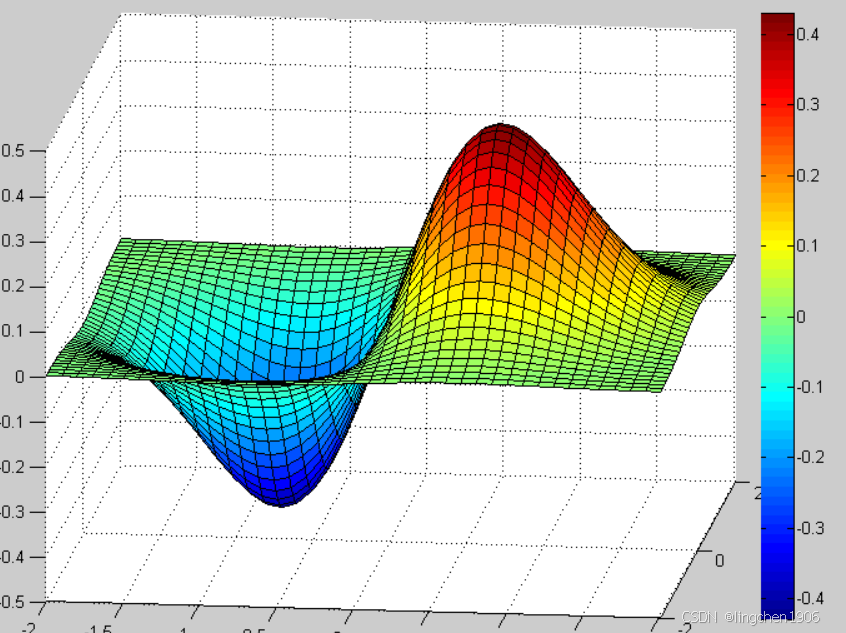
2. 三维曲面

需先通过meshgrid生成网格数据，再用mesh（网格曲面）或surf（着色曲面）绘制。示例：绘制抛物面 z=x²+y²

[x, y] = meshgrid(-2:0.1:2);  % 生成x、y的网格（范围-2到2）
z = x .^ 2 + y .^ 2;          % 抛物面公式
surf(x, y, z);  % 绘制着色曲面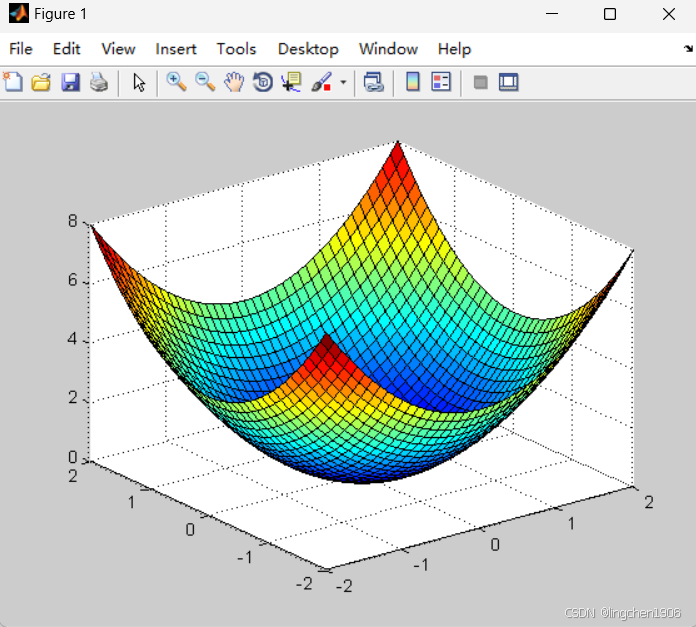

（3）、多维图形绘制

对于超过三维的数据（如 4 维及以上），MATLAB 2010b 通过 “降维可视化” 实现，常用方式：

• 用颜色表示第四维：在三维图形中，通过colormap将第四维数据映射为颜色；
• 切片展示：用slice函数对高维体数据进行切片，显示某一维度的截面。

示例：4 维数据可视化（x,y,z 为空间坐标，c 为第四维颜色）

[x, y, z] = meshgrid(-1:0.2:1);  % 三维网格
c = x .* exp(-(x.^2 + y.^2 + z.^2));  % 第四维数据（颜色）
slice(x, y, z, c, [0], [0], [-0.5 0 0.5]);  % 在x=0、y=0、z=-0.5/0/0.5处切片
colormap(jet);  % 用jet颜色映射表示第四维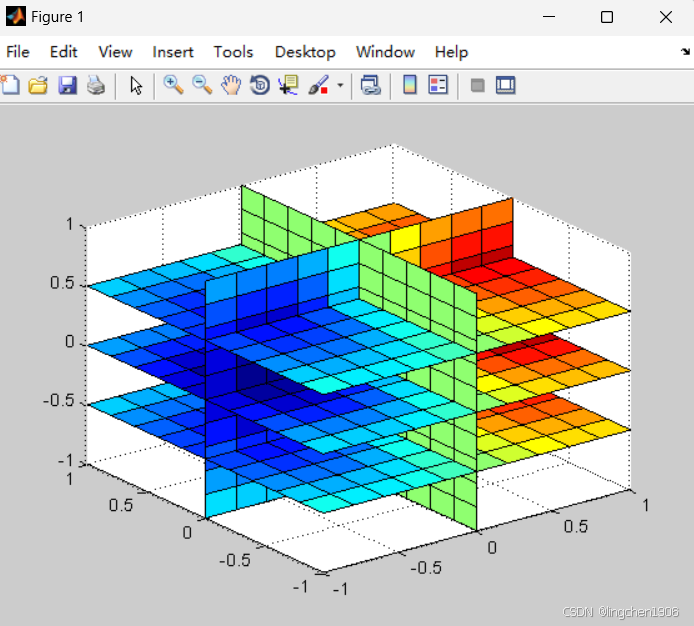

（4）、图形修饰功能

MATLAB 2010b 提供丰富的修饰函数，可美化图形、增强可读性，核心功能包括：

示例：修饰二维正弦曲线

x = 0:0.1:2*pi;
y = sin(x);
plot(x, y, 'r-', 'LineWidth', 2);  % 红色实线，线宽2
xlabel('x（弧度）');  % x轴标签
ylabel('sin(x)');     % y轴标签
title('正弦曲线');     % 标题
legend('y=sin(x)');   % 图例
grid on;              % 显示网格
axis tight;           % 坐标轴适应数据范围

总结

MATLAB 2010b 通过plot/polar/loglog等函数支持多坐标系的二维绘图，用plot3/mesh/surf实现三维图形，通过颜色映射或切片处理多维数据，同时提供完整的图形修饰工具，可满足从基础到复杂的可视化需求。

一、基本的二维图像

MATLAB最常用的二维绘图命令是plot，在直角坐标系下能够实现描点连线的绘图功能，调用格式为plot（x，y）。

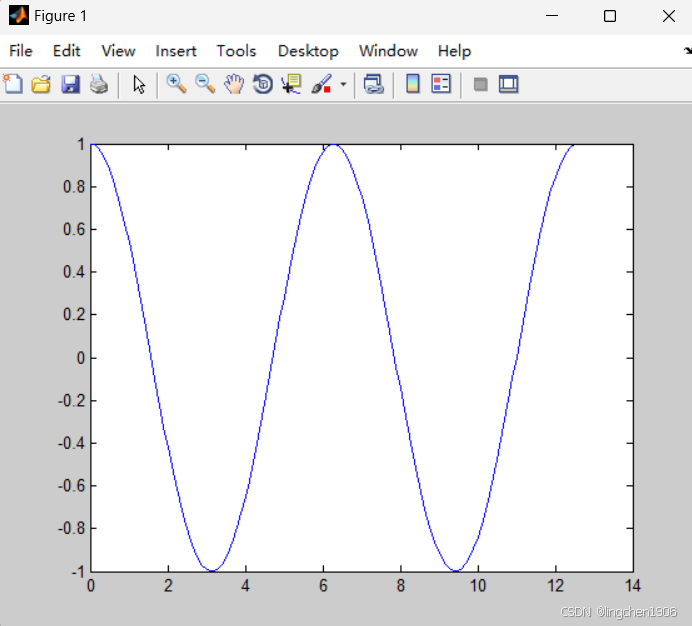
例：请绘制x在[0，4]的范围内，y=cos x的图形。

x=0：0.1：4*pi；

y=cos（x）；

plot（x，y）

x=0：/180：4*pi；

x=0：1：4*pi；