（数据结构）栈和队列

栈

概念与理解

栈是⼀种特殊的线性表，其只允许在固定的⼀端进行插入和删除元素操作。
进行数据插入和删除操作的⼀端称为栈顶，另⼀端称为栈底。

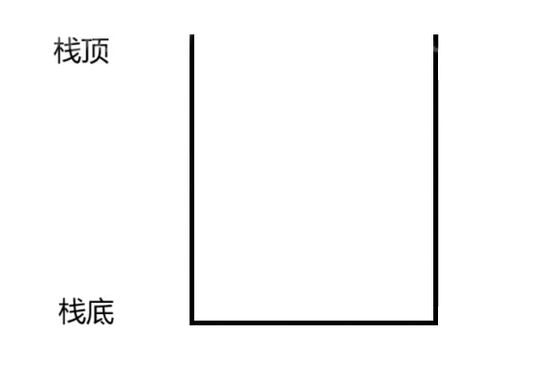
栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。
压栈：栈的插入操作叫做进栈/压栈/入栈
出栈：栈的删除操作叫做出栈。
出入数据都在栈顶。

栈的实现⼀般可以使用数组或者链表实现，相对而言数组的结构实现更优⼀些。因为数组在尾上插入数据的代价比较小。

作为特殊的线性表，栈的逻辑结构必然是线性的，物理结构上，若我们选择使用数组实现，则物理结构也是线性的。

实现

• 注意以下几个重点即可轻松实现：

1. 数组的右边作为栈顶，元素从数组的左边开始入栈
2. 栈包括一个数组、栈顶序号和容量大小
3. 当top==capacity时，说明栈满，需要增容

结构与方法

typedef int STDataType;
typedef struct Stack
{STDataType* arr;int top;int capacity;
}ST;//初始化
void STinit(ST* ps);
//销毁
void STDestroy(ST* ps);
//判断栈是否为空
bool StackEmpty(ST* ps);
//入栈
void StackPush(ST* ps, STDataType x);
//出栈
void StackPop(ST* ps);
//取栈顶数据
STDataType StackTop(ST* ps);
//获取栈中有效数据个数
int STSize(ST* ps);

具体实现

//初始化
void STinit(ST* ps)
{ps->arr = NULL;ps->top = ps->capacity = 0;
}//入栈_只会在栈顶入栈
void StackPush(ST* ps, STDataType x) 
{assert(ps != NULL);if (ps->top == ps->capacity) {//不要直接替换top和capacity！因为有可能realloc失败导致数据丢失！int newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;STDataType* tmp = (STDataType*)realloc(ps->arr, newCapacity*sizeof(STDataType));if (!tmp) {perror("realloc fail!");exit(1);}//realloc成功再替换ps->arr = tmp;ps->capacity = newCapacity;}ps->arr[ps->top++]=x;
}//判断栈是否为空
bool StackEmpty(ST* ps)
{assert(ps);return ps->top == 0;
}//出栈
void StackPop(ST* ps)
{assert(!StackEmpty(ps)); ps->top--;
}//取栈顶数据
STDataType StackTop(ST* ps)
{assert(!StackEmpty(ps));return ps->arr[ps->top - 1];
}//获取栈中有效数据个数
int STSize(ST* ps)
{assert(ps);return ps->top;
}
//销毁
void STDestroy(ST* ps)
{if (ps->arr)free(ps->arr);ps->arr = NULL;ps->top = ps->capacity = 0;
}

算法题

有效的括号

https://leetcode.cn/problems/valid-parentheses/description/
给定一个只包括 ‘(’，‘)’，‘{’，‘}’，‘[’，‘]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。

• 为什么可以用栈解决？
  对一个示例([ ])
  我们以相同括号为整体一分为二
  ([ ])我们发现，左边的顺序是小括号、中括号，而右边的顺序就是中括号、小括号，我们对比一下顺序，发现和栈“先进后出”的特点是十分相似的。至此我们找到了“有效字符串”规则与栈的高度相似性。

• 转化思路：
  对输入的字符串进行检索，遇到左括号时将其入栈，遇到右括号，就出栈将左括号和右括号进行配对，如果匹配就继续检索，如果不匹配直接return false。
  最终检索结束，还要检查栈是否为空，保证每个括号都是一一成对的。

参考解法

typedef char STDataType;
typedef struct Stack
{STDataType* arr;int top;int capacity;
}ST;
//初始化
void STinit(ST* ps)
{ps->arr = NULL;ps->top = ps->capacity = 0;
}//入栈_只会在栈顶入栈
void StackPush(ST* ps, STDataType x) 
{assert(ps != NULL);if (ps->top == ps->capacity) {//不要直接替换top和capacity！因为有可能realloc失败导致数据丢失！int newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;STDataType* tmp = (STDataType*)realloc(ps->arr, newCapacity*sizeof(STDataType));if (!tmp) {perror("realloc fail!");exit(1);}//realloc成功再替换ps->arr = tmp;ps->capacity = newCapacity;}ps->arr[ps->top++]=x;
}//判断栈是否为空
bool StackEmpty(ST* ps)
{assert(ps);return ps->top == 0;
}//出栈
void StackPop(ST* ps)
{assert(!StackEmpty(ps)); ps->top--;
}//取栈顶数据
STDataType StackTop(ST* ps)
{assert(!StackEmpty(ps));return ps->arr[ps->top - 1];
}//获取栈中有效数据个数
int STSize(ST* ps)
{assert(!StackEmpty(ps));return ps->top;
}
//销毁
void STDestroy(ST* ps)
{if (ps->arr)free(ps->arr);ps->arr = NULL;ps->top = ps->capacity = 0;
}bool isValid(char* s) {ST st;STinit(&st);//遍历给定的字符串schar* pi=s;while(*pi!='\0'){//左括号入栈if(*pi=='('||*pi=='['||*pi=='{')StackPush(&st,*pi);//否则遇到右括号出栈else{if(StackEmpty(&st)){STDestroy(&st);return false;}char top=StackTop(&st);if((top=='('&&*pi!=')')||(top=='['&&*pi!=']')||(top=='{'&&*pi!='}')){STDestroy(&st);return false;}StackPop(&st);}pi++;}//保证括号都配对if(StackEmpty(&st)){STDestroy(&st);return true;}//别忘了处理没通过的情况！elsereturn false;
}

队列

概念与理解

概念：只允许在⼀端进行插入数据操作，在另⼀端进行删除数据操作的特殊线性表，队列具有先进先出FIFO(First In First Out)
⼊队列：进行插入操作的⼀端称为队尾
出队列：进行删除操作的⼀端称为队头

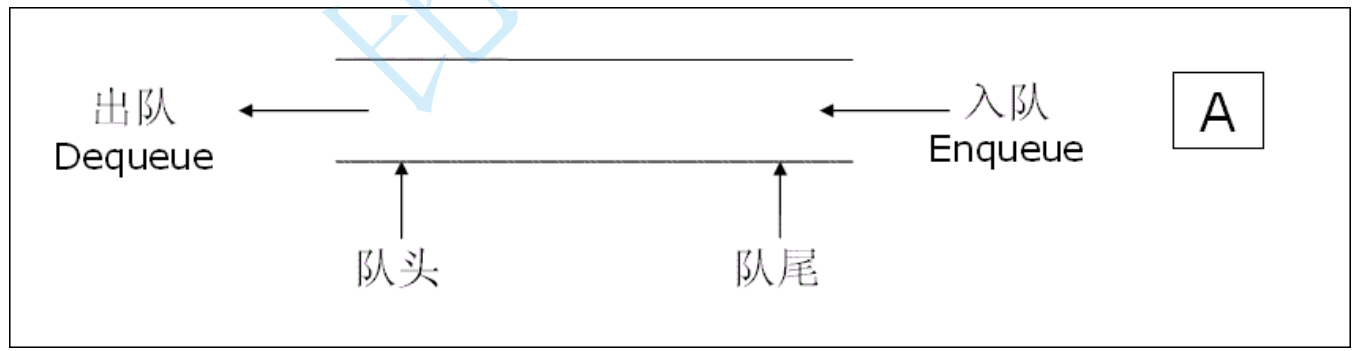
结构分析

首先要判断队列的底层要用数组还是链表实现，使用数组的话，必然会在头删/头插的情况下出现时间复杂度为O（n）的操作，所以不考虑，使用单链表如下：

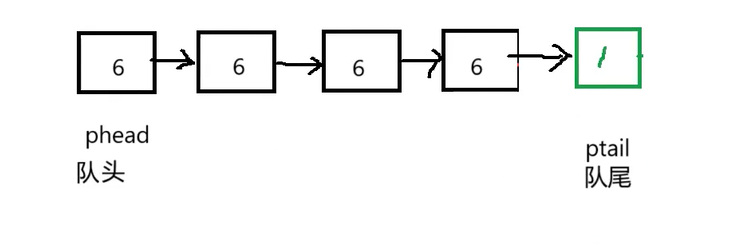
如果认为链表的头为队头，链表的尾为队尾，计算一下队尾入队的时间复杂度=尾插=O(n),而出队的时间复杂度=头删=O(1)，如此一看链表似乎并没有在结构上优于数组，但是我们可以对此进行优化：
尾插时间复杂度为O(n)的原因是，对于常规的单链表结构，我们只存储了头结点，所以每次尾插都需要遍历到尾结点才能进行插入，但如果我们把尾结点也存储起来并进行同步的更新，尾插时间复杂度就可优化为O(1)
经过分析后获得入队和出队时间复杂度都为O(1)的链表结构如下：

typedef int QDataType; 
typedef struct QueneNode {QDataType data;struct QueneNode* next;
}QueneNode;
//定义队列的结构
typedef struct Quene {struct QueneNode* phead;//队头struct QueneNode* ptail;//队尾
}Quene;

实现

结构与方法

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>typedef int QDataType; 
typedef struct QueueNode {QDataType data;struct QueueNode* next;
}QueueNode;
typedef struct Queue {struct QueueNode* phead;//队头struct QueueNode* ptail;//队尾int size;//记录有效数据个数（降低求队列大小的算法的时间复杂度）//如果需要频繁调用队列大小的话，就在队列结构加入size，调用得少的话可以不加入
}Queue;//初始化
void QueueInit(Queue* pq);
//入队——队尾
void QueuePush(Queue* pq, QDataType x);
//判空操作——删除必备
bool QueueEmpty(Queue* pq);
//出队——队头
void QueuePop(Queue* pq);
//取队头数据
QDataType QueueFront(Queue* pq);
//取队尾数据
QDataType QueueBack(Queue* pq);
//销毁
void QueueDestroy(Queue* pq);
//队列有效数据个数
int QueueSize(Queue* pq);

具体实现

//初始化
void QueueInit(Queue* pq) 
{assert(pq);pq->phead = pq->ptail = NULL;
}  
//入队——队尾
void QueuePush(Queue* pq, QDataType x)
{assert(pq);QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));if (newnode == NULL) {perror("malloc error");exit(1);}newnode->data = x;newnode->next = NULL;//队列为空，newnode既是队头也是队尾if (pq->phead = NULL) {pq->phead = pq->ptail = newnode;}//队列非空,直接插入到队尾else {pq->ptail->next = newnode;pq->ptail = pq->ptail->next;//记得更新ptail}pq->size++;
}//判空操作——删除必备
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->phead==NULL;
}
//出队——队头
void QueuePop(Queue* pq)
{assert(!QueueEmpty(pq));//只有一个结点的情况if (pq->phead == pq->ptail) {free(pq->phead);pq->phead = pq->ptail=NULL;}else {QueueNode* next = pq->phead->next;free(pq->phead);pq->phead = next;}	pq->size--;
}//取队头数据
QDataType QueueFront(Queue* pq)
{assert(!QueueEmpty(pq));return pq->phead->data;
}
//取队尾数据
QDataType QueueBack(Queue* pq)
{assert(!QueueEmpty(pq));return pq->ptail->data;
}//销毁
void QueueDestroy(Queue* pq)
{assert(pq);QueueNode* pcur = pq->phead;while (pcur) {QueueNode* next = pcur->next;free(pcur);pcur = next;}pq->phead = pq->ptail = NULL;
}//队列有效数据个数
int QueueSize(Queue* pq)
{return pq->size;
}

算法题

用队列实现栈

https://leetcode.cn/problems/implement-stack-using-queues/description/

题目：请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：
void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

注意：
你只能使用队列的标准操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。 你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

思路：首先明确需要实现的功能有什么：

1. void push(int x) 将元素 x 压入栈顶
2. int pop() 移除并返回栈顶元素
3. int top() 返回栈顶元素
4. boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

其次明确我们的工具是两个队列，思考实现方式。
入栈：可以直接等效为入队
出栈：出栈与出队顺序就不一样了，我们画图模拟出栈顺序

返回栈顶元素：使用取队尾操作

• 循环状态：出栈结束后，两个队列又回到一个存储元素，一个为空的状态，同样的初始状态便于出栈操作的进行

示例代码：

typedef int QDataType; 
typedef struct QueueNode {QDataType data;struct QueueNode* next;
}QueueNode;
typedef struct Queue {struct QueueNode* phead;//队头struct QueueNode* ptail;//队尾int size;//记录有效数据个数（降低求队列大小的算法的时间复杂度）//如果需要频繁调用队列大小的话，就在队列结构加入size，调用得少的话可以不加入
}Queue;typedef struct {Queue q1;Queue q2;
} MyStack;//初始化
void QueueInit(Queue* pq) 
{assert(pq);pq->phead = pq->ptail = NULL;pq->size = 0;
}  
//入队——队尾
void QueuePush(Queue* pq, QDataType x)
{assert(pq);QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));if (newnode == NULL) {perror("malloc error");exit(1);}newnode->data = x;newnode->next = NULL;//队列为空，newnode既是队头也是队尾if (pq->phead == NULL) {pq->phead = pq->ptail = newnode;}//队列非空,直接插入到队尾else {pq->ptail->next = newnode;pq->ptail = pq->ptail->next;//记得更新ptail}pq->size++;
}//判空操作——删除必备
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->phead==0;
}
//出队——队头
void QueuePop(Queue* pq)
{assert(!QueueEmpty(pq));//只有一个结点的情况if (pq->phead == pq->ptail) {free(pq->phead);pq->phead = pq->ptail=NULL;}else {QueueNode* next = pq->phead->next;free(pq->phead);pq->phead = next;}	pq->size--;
}//取队头数据
QDataType QueueFront(Queue* pq)
{assert(!QueueEmpty(pq));return pq->phead->data;
}
//取队尾数据
QDataType QueueBack(Queue* pq)
{assert(!QueueEmpty(pq));return pq->ptail->data;
}//销毁
void QueueDestroy(Queue* pq)
{assert(pq);QueueNode* pcur = pq->phead;while (pcur) {QueueNode* next = pcur->next;free(pcur);pcur = next;}pq->phead = pq->ptail = NULL;
}//队列有效数据个数
int QueueSize(Queue* pq)
{return pq->size;
}MyStack* myStackCreate() {MyStack* ms=(MyStack*)malloc(sizeof(MyStack));QueueInit(&ms->q1);QueueInit(&ms->q2);return ms;
}void myStackPush(MyStack* obj, int x) {if(!QueueEmpty(&obj->q1)){QueuePush(&obj->q1,x);}else{QueuePush(&obj->q2,x);}
}int myStackPop(MyStack* obj) {Queue* emp=&obj->q1;Queue* noemp=&obj->q2;if(!QueueEmpty(&obj->q1)){emp=&obj->q2;noemp=&obj->q1;}while(noemp->size>1){QueuePush(emp,QueueFront(noemp));QueuePop(noemp);}int top=QueueFront(noemp);QueuePop(noemp);//最后一定要把这个队列清空，保证后面好判定谁是存储元素的队列return top;
}int myStackTop(MyStack* obj) {if(!QueueEmpty(&obj->q1)){return QueueBack(&obj->q1);}else{return QueueBack(&obj->q2);}
}bool myStackEmpty(MyStack* obj) {return QueueEmpty(&obj->q1)&&QueueEmpty(&obj->q2);
}void myStackFree(MyStack* obj) {QueueDestroy(&obj->q1);QueueDestroy(&obj->q2);
}

用栈实现队列

https://leetcode.cn/problems/implement-queue-using-stacks/description/

需要完成队列的入队、出队、取队头、判空的操作。
我们依旧要思考栈与队列不同的点和栈本身的特点。
队列的入队与出队顺序相同，而栈的入栈出栈顺序相反，我们可以利用这个特点，用两次出栈使最终出栈的元素顺序与最开始入栈顺序相同，即实现了入队操作。我们称左边第一次入栈进入的是pushST，第二次入栈进入的是popST，因为最终这个栈弹出的元素是出队的元素顺序。

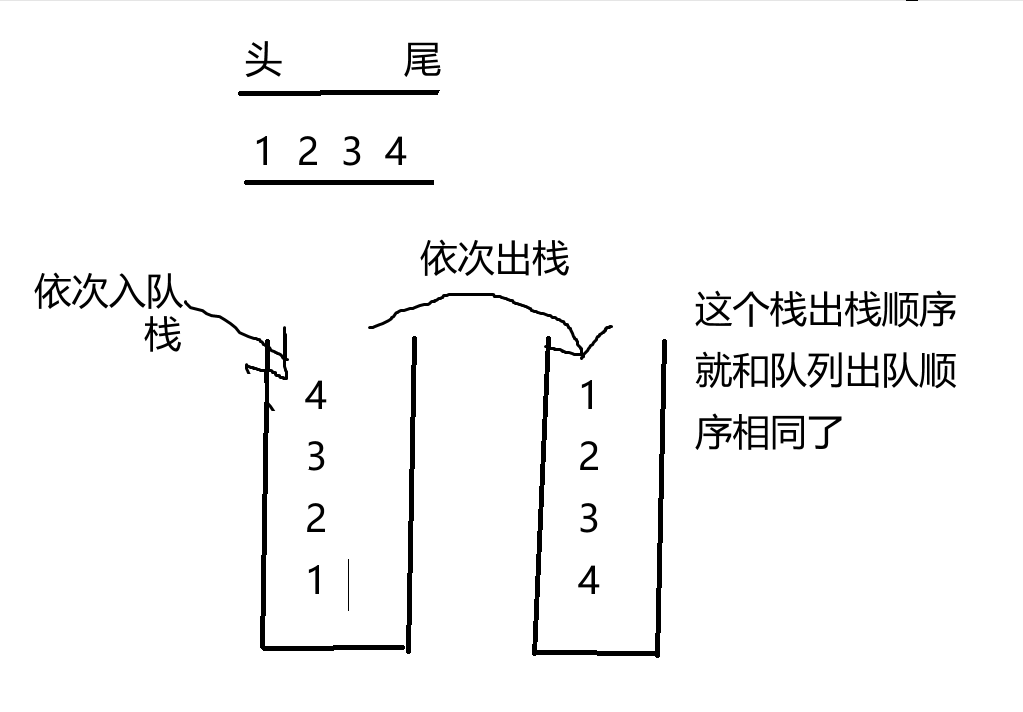
综上，入队=往pushST中插入数据
出队=popST不为空时直接出栈，为空时将pushST中的数据导入到popST后出栈
取队头=只取数据不pop的出队操作

typedef int STDataType;
typedef struct Stack
{STDataType* arr;int top;int capacity;
}ST;//初始化
void STinit(ST* ps);
//销毁
void STDestroy(ST* ps);
//判断栈是否为空
bool StackEmpty(ST* ps);
//入栈
void StackPush(ST* ps, STDataType x);
//出栈
void StackPop(ST* ps);
//取栈顶数据
STDataType StackTop(ST* ps);
//获取栈中有效数据个数
int STSize(ST* ps);typedef struct {ST pushST;ST popST;   
} MyQueue;//初始化
void STinit(ST* ps)
{ps->arr = NULL;ps->top = ps->capacity = 0;
}//入栈_只会在栈顶入栈
void StackPush(ST* ps, STDataType x) 
{assert(ps != NULL);if (ps->top == ps->capacity) {//不要直接替换top和capacity！因为有可能realloc失败导致数据丢失！int newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;STDataType* tmp = (STDataType*)realloc(ps->arr, newCapacity*sizeof(STDataType));if (!tmp) {perror("realloc fail!");exit(1);}//realloc成功再替换ps->arr = tmp;ps->capacity = newCapacity;}ps->arr[ps->top++]=x;
}//判断栈是否为空
bool StackEmpty(ST* ps)
{assert(ps);return ps->top == 0;
}//出栈
void StackPop(ST* ps)
{assert(!StackEmpty(ps)); ps->top--;
}//取栈顶数据
STDataType StackTop(ST* ps)
{assert(!StackEmpty(ps));return ps->arr[ps->top - 1];
}//获取栈中有效数据个数
int STSize(ST* ps)
{assert(ps);return ps->top;
}
//销毁
void STDestroy(ST* ps)
{if (ps->arr)free(ps->arr);ps->arr = NULL;ps->top = ps->capacity = 0;
}MyQueue* myQueueCreate() {MyQueue* mq=(MyQueue*)malloc(sizeof(MyQueue));STinit(&mq->pushST);STinit(&mq->popST);return mq;
}void myQueuePush(MyQueue* obj, int x) {StackPush(&obj->pushST,x);
}int myQueuePop(MyQueue* obj) {if(StackEmpty(&obj->popST)){while(STSize(&obj->pushST)){StackPush(&obj->popST,StackTop(&obj->pushST));StackPop(&obj->pushST);}}int top=StackTop(&obj->popST);StackPop(&obj->popST);return top;
}int myQueuePeek(MyQueue* obj) {if(StackEmpty(&obj->popST)){while(STSize(&obj->pushST)){StackPush(&obj->popST,StackTop(&obj->pushST));StackPop(&obj->pushST);}}return StackTop(&obj->popST);
}bool myQueueEmpty(MyQueue* obj) {return StackEmpty(&obj->pushST)&&StackEmpty(&obj->popST);
}void myQueueFree(MyQueue* obj) {STDestroy(&obj->pushST);STDestroy(&obj->popST);
}

循环队列

https://leetcode.cn/problems/design-circular-queue/description/
循环队列首尾相连成环

• 循环队列特点：

1. 队头删数据，队尾插入数据
2. 给定固定的空间，使用过程中不可以扩容（这一点很适合用数组实现）
3. 循环队列满了，不能继续插入数据（即插入数据失败）

• 实现
  循环队列可以用数组实现，也可以用循环链表实现。
  对比：哪个底层结构更好一点？数组的实现会更简便（不需要一个个开辟结点，存取数据方便）
  如何判断队列为空为满？——增加一个空间
  
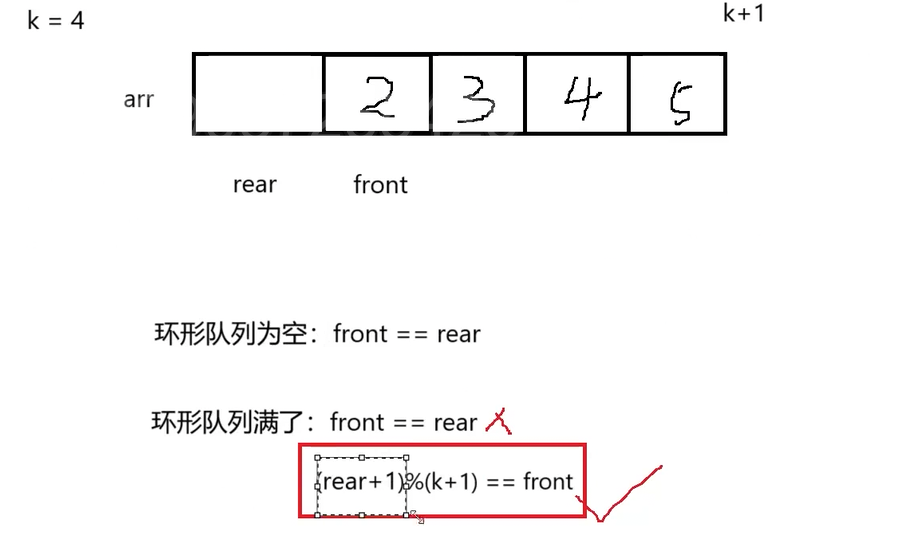
  示例代码

typedef struct {int* arr;int front;int rear;int capacity;
} MyCircularQueue;bool myCircularQueueIsEmpty(MyCircularQueue* obj) {return obj->front==obj->rear;
}bool myCircularQueueIsFull(MyCircularQueue* obj) {return (obj->rear+1)%(obj->capacity+1)==obj->front;
}MyCircularQueue* myCircularQueueCreate(int k) {MyCircularQueue* pq=(MyCircularQueue*)malloc(sizeof(MyCircularQueue)*(k+1));pq->arr=(int*)malloc(sizeof(int)*(k+1));pq->front=pq->rear=0;pq->capacity=k;return pq;
}bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {//空间有限，插入前先判满！if(myCircularQueueIsFull(obj)){return false;}//没有满obj->arr[obj->rear++]=value;obj->rear%=obj->capacity+1;//处理超过capacity+1的情况return true;
}bool myCircularQueueDeQueue(MyCircularQueue* obj) {//删除前判空if(myCircularQueueIsEmpty(obj)){return false;}//删除=出队，是对队头进行操作！obj->front++;obj->front%=obj->capacity+1;return true;
}int myCircularQueueFront(MyCircularQueue* obj) {if(myCircularQueueIsEmpty(obj))return -1;return obj->arr[obj->front];
}int myCircularQueueRear(MyCircularQueue* obj) {if(myCircularQueueIsEmpty(obj))return -1;if(obj->rear==0)return obj->arr[obj->capacity];return obj->arr[obj->rear-1];
}void myCircularQueueFree(MyCircularQueue* obj) {if(obj->arr)free(obj->arr);free(obj);obj=NULL;
}