算法：并行课程II

题目

给你一个整数 n 表示某所大学里课程的数目，编号为 1 到 n ，数组 relations 中， relations[i] = [xi, yi]  表示一个先修课的关系，也就是课程 xi 必须在课程 yi 之前上。同时你还有一个整数 k 。

在一个学期中，你 最多 可以同时上 k 门课，前提是这些课的先修课在之前的学期里已经上过了。

请你返回上完所有课最少需要多少个学期。题目保证一定存在一种上完所有课的方式。

示例 1：

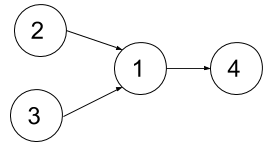
输入：n = 4, relations = [[2,1],[3,1],[1,4]], k = 2
输出：3 
解释：上图展示了题目输入的图。在第一个学期中，我们可以上课程 2 和课程 3 。然后第二个学期上课程 1 ，第三个学期上课程 4 。

题解

思路：动态规划

class Solution {public int minNumberOfSemesters(int n, int[][] relations, int k) {int[] d = new int[n + 1];//预处理要该门课程依赖哪些课程for (int[] e : relations) {d[e[1]] |= 1 << e[0];}Deque<int[]> q = new ArrayDeque<>();q.offer(new int[] {0, 0});//记录已经学习的课程Set<Integer> vis = new HashSet<>();vis.add(0);while (!q.isEmpty()) {int[] p = q.pollFirst();//cur已经学过的课程 已经学了几个学期int cur = p[0], t = p[1];//都学完了if (cur == (1 << (n + 1)) - 2) {return t;}//找到可以学的课程int nxt = 0;for (int i = 1; i <= n; ++i) {//已经学的课程和该门课依赖的课程做&运算后的值为d[i]，说明依赖的课程已经学完//可以学习该门课程了if ((cur & d[i]) == d[i]) {nxt |= 1 << i;}}//剔除学过的课程nxt ^= cur;//可以学的课程数就是nxt转二进制后1的数量，如果数量<=k，则把可以学的全部学完if (Integer.bitCount(nxt) <= k) {if (vis.add(nxt | cur)) {q.offer(new int[] {nxt | cur, t + 1});}} else {int x = nxt;//循环枚举nxt的子集while (nxt > 0) {//子集的二进制1的数量为K,且nxt | cur的值还没有计算过。则往队列中加入新节点if (Integer.bitCount(nxt) == k && vis.add(nxt | cur)) {//新节点：已经学的课程，需要的课程数q.offer(new int[] {nxt | cur, t + 1});}//求下一个子集nxt = (nxt - 1) & x;}}}return 0;}
}