【DecEx-RAG】

Decision and Execution Optimization via Process Supervision)

1 引言

当前最先进的大型语言模型（LLMs）已经展现出卓越的问题求解能力（Jaech 等, 2024；Shi 等, 2024；DeepSeek-AI 等, 2025）。然而，由于静态训练数据的固有限制，LLMs 在处理动态与实时性问题时仍存在显著瓶颈（Ji 等, 2023；Huang 等, 2025a）。检索增强生成（Retrieval-Augmented Generation, RAG） 通过引入外部知识库或搜索引擎，为解决这一问题提供了有前景的方向（Gao 等, 2023）。

近期的研究利用结果监督的强化学习（Outcome-supervised Reinforcement Learning, RL） 将动态检索过程融入推理流程，使 LLMs 能够自主调用检索工具并取得显著成果（Jin 等, 2025；Song 等, 2025）。然而，这类方法仍然存在内在局限性：

1. 探索效率低 —— LLM 必须生成完整的推理链后，才能根据最终结果获得奖励反馈。
2. 奖励信号稀疏 —— 稀疏的奖励导致模型需要更多的数据与训练步数才能收敛（Zhang 等, 2025）。
3. 全局奖励缺乏细粒度性 —— 全局奖励难以反映推理步骤级的局部表现，从而阻碍了细粒度优化。

受人类利用搜索工具解决复杂问题方式的启发，我们提出了 DecExRAG —— 一种面向 Agentic RAG 的过程监督框架（Process-supervised Framework）。
该框架将 RAG 建模为一个马尔可夫决策过程（Markov Decision Process, MDP），并包含两个阶段：决策阶段（Decision-Making） 与 执行阶段（Execution）。

---

一、决策阶段（Decision-Making）

该阶段包括两类关键决策：

• 终止决策（Termination Decision）：用于避免冗余迭代或过早停止；
• 检索决策（Retrieval Decision）：用于判断是否依赖 LLM 的内部知识，或调用外部检索工具解决子问题。

二、执行阶段（Execution）

该阶段关注决策执行的质量。例如，高质量的子问题生成对于后续推理的成功至关重要。
通过结构化地分解决策阶段与执行阶段，DecExRAG 能够实现过程级的细粒度监督，同时兼顾执行质量与决策效率。

---

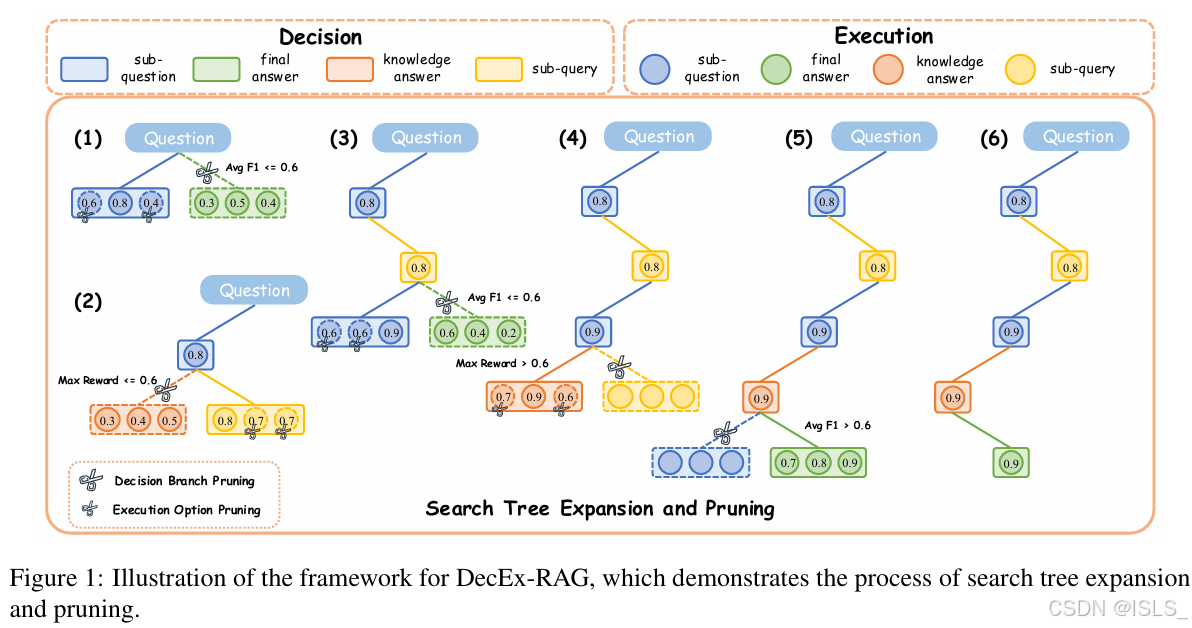
在 DecExRAG 框架中，由于中间推理步骤缺乏监督信号，模型在搜索树扩展过程中往往需要大量探索，导致时间复杂度随层深呈指数级增长。为解决该问题，我们提出了一种高效的剪枝策略（Pruning Strategy）。

在搜索树的每一层中，框架针对不同决策执行路径进行多次 rollout 模拟，并使用**聚合奖励（Aggregated Rewards）**作为反馈信号，动态剪除冗余分支。
具体而言：

• 当终止决策判断当前迭代信息已足以回答问题时，迭代过程终止；
• 当检索决策判断模型的内在知识足以推导最终答案时，跳过检索操作。

---

为验证 DecExRAG 框架及所提剪枝策略的有效性，我们在 六个开放域问答数据集 上进行了实验。结果表明，DecExRAG 的平均性能较结果监督强基线模型 Search-R1（Jin 等, 2025） 提升 6.3%。
进一步分析发现，所提出的剪枝策略在保持数据质量不变的前提下，使得数据构建效率提升近 6 倍，充分证明了该方法的有效性与实用性。

---

总结而言，我们的主要贡献如下：

• 提出 DecEx-RAG 框架：将 RAG 建模为马尔可夫决策过程（MDP），为 Agentic RAG 系统提供了更全面、统一的建模视角。
• 提出剪枝策略：优化数据扩展过程，在不降低数据质量的前提下显著提升过程监督数据构建效率。
• 实验验证：在六个数据集上，在相同规模的训练数据下，DecEx-RAG 的整体性能显著优于现有基线方法。

---

是否希望我将这一中文版本润色为正式的论文摘要风格（例如可直接放入学术论文中）？

2 DecEx-RAG

图1展示了我们提出的 DecEx-RAG 框架。
该框架将 RAG（Retrieval-Augmented Generation，检索增强生成）建模为一个包含决策与执行机制的马尔可夫决策过程（Markov Decision Process, MDP），通过为每个问题扩展搜索树来获得多步过程监督数据。

在扩展过程中，通过多次 rollout 获取中间过程奖励，并剪枝冗余分支以提升效率。
当扩展完成后，从根节点到叶节点的最优推理链用于监督微调（Supervised Fine-tuning, SFT），而路径上的所有分支节点则作为**直接偏好优化（Direct Preference Optimization, DPO）**的数据。

---

2.1 将 RAG 建模为马尔可夫决策过程

我们将 RAG 形式化为一个马尔可夫决策过程，用四元组 $(S,A,P,R)$ 表示：

• $S$ 表示状态集合；
• $A$ 表示动作集合；
• $P$ 描述状态转移动态；
• $R$ 指定奖励函数。

---

状态（States）

在每个时间步 $t$，状态 $s_t\in S$ 表示当前问题的部分解。
形式化地，状态 $s_t$ 可以表示为：

$$s_t=[Q,(q_1,r_1),\cdots ,(q_t,r_t)]$$

其中：

• $Q$ 是原始问题；
• $q_i$ 表示第 $i$ 个子问题；
• $r_i$ 表示 $q_i$ 的答案，或者是子查询及其检索到的相关文档。

---

动作（Actions）

在状态 $s_t$ 下，模型选择动作 $a_t=({\sigma }_t,{\delta }_t)\in A$，该动作包含两个决策：

• 终止决策 ${\sigma }_t$：决定是否继续迭代。

  • 若选择继续，则生成下一个子问题 $q_{t+1}$；
  • 若选择终止，则输出最终答案 $o$。

• 检索决策 ${\delta }_t$（当 ${\sigma }_t$ 选择继续时触发）：

  • 针对子问题 $q_{t+1}$，${\delta }_t$ 决定如何作答。
  • 若选择使用模型自身知识回答，则生成答案 $w_{t+1}$；
  • 若调用检索器，则生成子查询 $e_{t+1}$ 并获取相关文档 $d_{t+1}$。

---

状态转移（State Transition）

当在状态 $s_t$ 执行动作 $a_t=({\sigma }_t,{\delta }_t)$ 时，状态更新为 $s_{t+1}$。

具体而言：

• 若终止决策 ${\sigma }_t$ 选择终止，则生成最终答案 $o$ 并结束迭代：

  $$s_{t+1}=[Q,(q_1,r_1),\cdots ,(q_t,r_t),o]$$

• 否则，DecEx-RAG 生成新的子问题 $q_{t+1}$ 并继续执行检索决策 ${\delta }_t$：

  • 若 ${\delta }_t$ 选择基于模型自身知识回答，则 $r_{t+1}=w_{t+1}$；
  • 若 ${\delta }_t$ 选择检索，则 $r_{t+1}=[e_{t+1},d_{t+1}]$。

最终，状态更新为：

$$s_{t+1}=[Q,(q_1,r_1),\cdots ,(q_t,r_t),(q_{t+1},r_{t+1})]$$

---

奖励（Rewards）

奖励函数 $R(s_t,a_t)$ 指定在状态 $s_t$ 采取动作 $a_t$ 后获得的期望奖励。

在我们的框架下，我们为每个状态-动作对 $(s_t,a_t)$ 执行多次 rollout，并以多次 rollout 结果的正确性作为奖励：

$$R(s_t,a_t)=\frac{1}{n}\sum _{i=1}^{n}v({\text{rollout}}_i)$$

其中：

• ${\text{rollout}}_i$ 表示第 $i$ 次对 $(s_t,a_t)$ 的模拟执行；
• $v({\text{rollout}}_i)\in [0,1]$ 表示最终答案的正确性得分（例如 F1 分数）。

---

框架创新点

我们的框架提出了两个关键创新：

1. 明确区分“子问题（sub-question）”与“子查询（sub-query）”。
   这种区分的重要性在于：不同检索器可能会对语义相近但细节不同的子查询返回截然不同的文档。
   因此，子查询被独立处理以优化检索效果。

2. 在 MDP 框架中解耦“决策”与“执行”过程。
   传统的 MDP 框架往往将决策与执行视为整体，缺乏明确区分。
   在 DecEx-RAG 中：

   • 决策部分专注于方法选择；
   • 执行部分专注于内容质量。

   通过将决策与执行解耦，我们能够利用决策数据提升系统效率，同时利用执行数据优化内容生成质量。

---

2.2 带剪枝的搜索树扩展（Search Tree Expansion with Pruning）

基于第 2.1 节中定义的马尔可夫决策过程（MDP），DecEx-RAG 通过构建 搜索树（search tree） 来求解每个问题。

在状态 $s_t$ 下，模型首先扩展终止决策 ${\sigma }_t$，并使用非零温度参数对该决策进行多次采样。
若超过 50% 的采样结果倾向于终止迭代，则求解过程结束；
否则，模型生成多个候选子问题（sub-questions）。

在对这些候选子问题进行去重后，针对每个子问题执行多次 rollout 模拟，取其平均得分作为中间奖励（intermediate reward），最终选择奖励最高的分支以扩展至下一个状态。

完成终止决策的扩展后，模型接着扩展检索决策 ${\delta }_t$。
在此阶段，模型首先基于自身知识生成多个候选答案，并对这些答案进行去重与多次 rollout 计算奖励。
若最高奖励超过预设阈值，则表明从当前状态即可正确推导出最终答案。
此时，为减少计算开销，将跳过检索分支，并直接选择该最高奖励答案作为下一个扩展状态。

否则，模型会生成多个子查询（sub-queries），重复上述过程，并选择奖励最高的子查询分支继续扩展。

搜索树扩展过程受最大迭代步数 $T_{max}$ 控制。
每一层均按上述策略执行，直至达到迭代上限或被模型主动终止。

虽然每个决策执行都需要多次 rollout 以获取中间奖励，但这些数据不仅用于构建偏好训练数据（preference data），也为**决策剪枝（decision pruning）**提供依据。
通过剪枝，每一层的搜索树仅保留最优决策分支，从而显著提升搜索树扩展效率。

所有用于搜索树扩展的提示指令（prompt instructions）均列于附录 A.1。

---

2.3 模型训练（Training）

DecEx-RAG 的训练聚焦于优化以下四个关键组件，覆盖框架中两类决策的所有分支：

1. 最终答案生成（Final Answer Generation）；
2. 子问题分解（Sub-question Decomposition）；
3. 基于自有知识的子问题回答（Sub-question Answering based on Self-Knowledge）；
4. 子查询生成与检索（Sub-query Generation and Retrieval）。

基于第 2.2 节构建的搜索树，我们执行两阶段训练（Two-stage Training）。

---

（1）监督微调（Supervised Fine-tuning, SFT）

我们从搜索树中提取从根节点到叶节点的完整推理路径，用于 SFT 训练。

对于每个问题 $Q$，我们构建多个输入-输出对：

• 输入包括：
  $$Q,(q_1,r_1),\dots ,(q_{x_i},e_{x_i},d_{x_i})$$
• 输出包括：
  $$(q_{x_i+1},r_{x_i+1}),\dots ,(q_{x_i+1},e_{x_i+1})$$

其中，$x_i$ 为检索步骤（retrieval step）的索引。
该设计确保了推理过程的迭代性（iterative reasoning），使得大语言模型（LLM）能够利用前一步的结果，直至下一次检索或最终答案生成。

---

（2）直接偏好优化（Direct Preference Optimization, DPO）

随后，我们利用搜索树节点中的决策与执行数据来构建偏好对（preference pairs）。

尽管最终的搜索树中每一层只保留最优分支，但在剪枝前，模型已生成了所有候选决策分支，因此我们自然获得了两类偏好数据（决策层和执行层）。

基于这些混合偏好数据，我们执行 DPO 训练。
其详细训练目标函数可见附录 A.2。

3 实验

3.1 数据集与基线模型

我们在六个公开数据集上对 DecEx-RAG 及所有基线模型进行了评估，其中包括

三个单跳问答（single-hop QA）数据集：

• PopQA（Mallen 等, 2023）、
• NQ（Kwiatkowski 等, 2019）和
• AmbigQA（Min 等, 2020）；

以及三个多跳问答（multi-hop QA）数据集：

• HotpotQA（Yang 等, 2018）、
• 2WikiMultiHopQA（Ho 等, 2020）和
• Bamboogle（Press 等, 2023）。

其中，HotpotQA 与 2WikiMultiHopQA 属于域内测试集（in-domain test sets），而其他四个数据集为跨域测试集（out-of-domain test sets）。

我们将 DecEx-RAG 与两类基线模型进行了对比：

• Prompt-based 方法（如 Direct Inference、Standard RAG、Search-o1）；
• 强化学习（RL）方法（如 Search-R1、IKEA、DeepRAG）。

更详细的基线信息可参见附录 B。

---

3.2 实现细节

我们从 HotpotQA 训练子集中抽取 2,000 条问题，从 2WikiMultiHopQA 训练子集中抽取 1,000 条问题，用于构建训练集。

在搜索树扩展过程中，对于检索决策（retrieval decisions），我们使用 Qwen2.5-7B-Instruct（Yang 等, 2024）作为策略模型，与后续训练阶段使用的基础模型保持一致。除此之外，其余决策阶段统一使用 Qwen3-30B-A3B（Yang 等, 2025）作为策略模型。

在检索阶段，我们遵循 Jin 等（2025）的设定，采用 2018 年 Wikipedia dump（Karpukhin 等, 2020）作为知识源，并使用 E5（Wang 等, 2022） 作为检索器。

为确保公平比较，我们复现了 Search-R1 与 IKEA，并保持训练数据规模一致。

对于所有需要检索的模型，检索文档数量固定为 3；对于所有多轮迭代方法，最大迭代步数 T_max 设为 4。

在评估指标上，我们采用 Exact Match (EM) 和 F1 分数 进行性能衡量。

---

3.3 主要结果

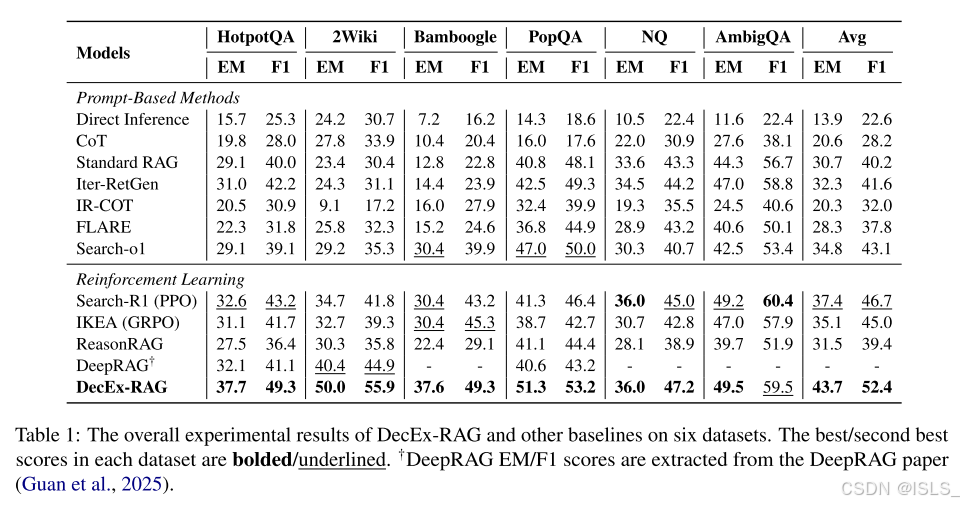
如表 1 所示，我们展示了 DecEx-RAG 与 11 个基线模型在六个数据集上的性能表现。根据实验结果，我们得出以下主要结论：

---

（1）基于 Prompt 的方法性能受限。

实验表明，仅依赖内部知识的方法（如 Direct Inference 与 CoT）表现较差，验证了 LLM 内在知识的局限性。
相比之下，基于 RAG 的方法（如 Iter-RetGen、IR-CoT、FLARE）取得了显著性能提升，说明引入外部知识的重要性。

值得注意的是，虽然 Search-o1 在所有 prompt-based 方法中表现最佳，但其优势远小于论文中报告的结果。这是因为 Search-o1 的复杂提示设计（prompting pipeline）对模型的指令跟随能力和推理能力要求极高，只有在大型推理模型上才能完全体现其优势；因此，其性能难以在较小模型上等比例迁移。

---

（2）过程监督强化学习（process-supervised RL）在数据效率上优于结果监督强化学习（outcome-supervised RL）。

虽然 Search-R1 与 IKEA 通过结果监督强化学习提升了模型在推理过程中调用搜索工具的能力，但在仅使用 3K 训练样本时，性能仍不理想。
相比之下，DecEx-RAG 在六个数据集上均表现出全面领先的性能，在相同训练数据规模下，平均性能提升 6%～8%，充分证明了过程监督 RL 的数据效率优势。

---

（3）DecEx-RAG 优于其他过程监督方法。

与其他过程监督方法（如 DeepRAG 与 ReasonRAG）相比，DecEx-RAG 表现更为优异。
其中，DeepRAG 仅关注决策优化，而 DecEx-RAG 同时覆盖决策与执行，形成更完整的优化框架。
对 ReasonRAG 输出的分析显示，其检索行为不足且过度依赖内部知识，导致错误答案增多。

实验结果表明，DecEx-RAG 不仅在域内测试集上表现出色，还展现出优秀的跨域泛化能力。

---

3.4 消融实验（Ablation Study）

为验证 DecEx-RAG 框架的有效性，我们进行了系列消融实验。

图 2(a) 展示了在 SFT 阶段 不同数据选择策略的比较结果。实验表明，采用 最高检索代价（Most Retrieval Cost, Most） 策略训练的模型性能最优，其检索行为更为频繁。
通过分析输出发现，该模型倾向于通过多次检索验证答案的正确性，表现出更强的审慎推理能力。
相反，采用 最低检索代价（Least Retrieval Cost, Least） 策略的模型过度依赖自身知识，错误率显著上升。

---

图 2(b) 展示了在 DPO 阶段 不同偏好数据组成的比较结果。实验发现，去除任一类偏好数据都会导致性能下降，说明决策与执行的联合优化是必要的。
进一步分析显示，使用决策数据训练的模型性能略低于使用执行数据训练的模型，但其检索次数更少。
这表明，执行数据 主要优化内容质量，而 决策数据 优化检索效率。

---

图 2 c 展示了不同训练方法的性能比较。
实验结果显示：

• 仅使用 SFT 训练 的模型能够学习到基本的检索模式，但检索频率不足限制了性能上限；
• 仅使用 DPO 训练 的模型由于缺乏有效的模仿学习，导致迭代质量较差、无效检索增多；
• 两阶段训练（SFT + DPO） 在性能与效率之间取得最佳平衡。SFT 阶段奠定推理基础，DPO 阶段优化决策过程，从而实现最佳整体性能。

4 分析

4.1 数据扩展效率

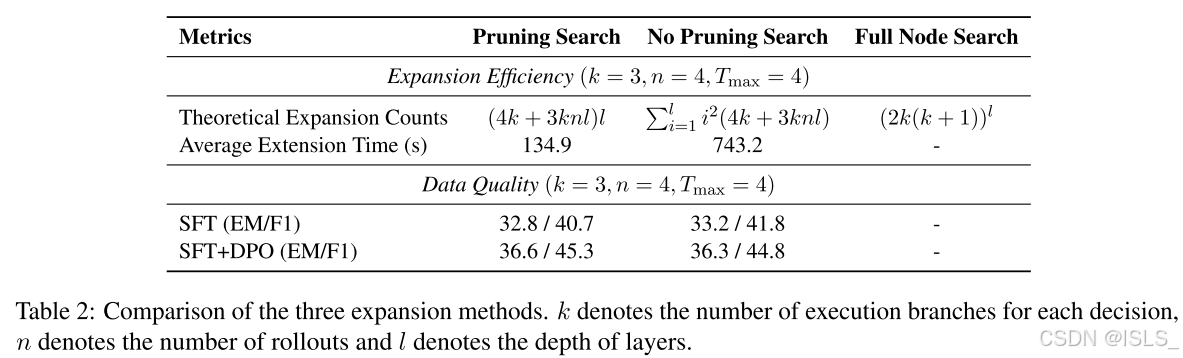
为验证搜索树扩展剪枝方法（Pruning Search）的有效性，我们将其与另外两种方法进行了比较：No Pruning Search 和 Full Node Search。

• No Pruning Search：保留两类决策的最优执行分支；
• Full Node Search：保留所有执行分支，但省略 rollout 模拟过程。

表 2 报告了所有实验结果。理论分析表明，Pruning Search 的扩展次数随层深呈线性增长，显著优于 No Pruning Search 的指数增长趋势 $2^l$，以及 Full Node Search 的更剧烈增长趋势 $(2k{)}^l$，其中 $k$ 表示每个决策的执行分支数，$l$ 表示层深。

在实际性能测试中，我们在相同硬件条件下使用 500 个问题评估三种方法。实验结果显示，Pruning Search 的平均扩展时间比 No Pruning Search 快近 6 倍。Full Node Search 的扩展效率极低，每个问题的扩展时间超过 1 小时，几乎无法比较，因此其后续实验结果未被报告。

为了进一步验证数据有效性，我们对 Pruning Search 与 No Pruning Search 生成的数据按相同数量进行抽样，并分别用于训练 Qwen2.5-7B-Instruct。表 2 显示了六个数据集上的平均性能。我们观察到，无论是仅 SFT 训练还是 SFT+DPO 训练，Pruning Search 与 No Pruning Search 生成的数据在模型性能上几乎一致。

总结来看，剪枝策略显著提升了扩展效率（近 6 倍），同时保持了与 No Pruning Search 相当的数据质量，充分体现了其有效性与实用价值。

---

4.2 剪枝对最优推理链的影响

通常情况下，剪枝操作可能会偏向局部最优的推理路径，同时舍弃潜在更优的全局推理路径。对于 RAG 任务而言，同一问题的不同推理路径的核心差异通常体现在决策阶段的选择上。

因此，我们对比了 Pruning Search 与 No Pruning Search 生成的最优推理链。实验发现：

• 85% 的样本在两种方法下迭代次数相同；
• 87% 的样本在两种方法下检索次数相同。

这些结果直接表明，所提剪枝策略在压缩搜索空间的同时，能够最大程度地保留全局最优的推理链。

---

4.3 案例分析

表 3 提供了一个案例，用于直观比较 DecEx-RAG 与 Search-R1 的性能差异。

对于给定问题，Search-R1 在依赖自身知识和一次检索的情况下，能够在推理过程中准确澄清 Ed Wood 与 Scott Derrickson 的国籍信息。然而，其最终输出结果为 “No”。这一现象清楚地表明 Search-R1 存在推理过程与结论严重不一致的问题，这是典型的**奖励操纵（reward hacking）**案例。

相比之下，DecEx-RAG 不仅生成了逻辑严谨且正确的推理过程，还实现了推理过程与最终答案之间的高度一致性。