当前位置： 首页 > news >正文

数据结构：顺序表讲解（2）

news 2025/10/25 6:51:33

目录

前言 

一、动态顺序表的实现（继续）

1.顺序表的指定位置查找

2.顺序表的销毁

3.顺序表的指定位置插入

4.顺序表的指定位置删除

代码逐行讲解

1. 参数与断言检查

2. 元素前移覆盖（核心逻辑）

3. 更新有效元素个数

5.实现的总代码

二、顺序表算法题

1.移除元素

核心逻辑：双指针法

步骤分解

2. 删除有序数组中的重复项

3.合并两个有序数组

总结

前言 

  数据结构：顺序表讲解文章将讲解顺序表介绍，顺序表分类，顺序表动态顺序表的实现，顺序表算法题，顺序表问题与思考知识的相关内容，其中顺序表介绍、顺序表概念与结构、顺序表分类、动态顺序表的实现、尾插，头插，尾删，头删时间复杂度对比为上一章节知识的内容，本章节将讲解剩余的知识：

一、动态顺序表的实现（继续）

在上篇博客中我们已经完成了顺序表的头插，尾插，头删，尾删等操作(数据结构：顺序表讲解（1）-CSDN博客)，本篇博客将讲解剩余的操作：

1.顺序表的指定位置查找

int Find(SL* h, type x);

int Find(SL* h, type x)
{assert(h);int i;for (i = 0; i < h->size; i++){if (h->arr[i] == x){return i;}}return -1;
}

解释：

  •  该函数用于在顺序表（SL）中查找指定元素 x，返回其下标（找到时）或 -1（未找到时），核心逻辑为遍历数组比较元素。

根据上篇文章：我们已经了解了尾插，头插，尾删，头删的内容，我们可以先实现一下代码操作：

但是我们在尾插，头插等操作时使用了malloc函数动态开辟内存，在结束程序时需要释放下开辟的空间，所以需要有销毁函数。

2.顺序表的销毁

void SLDestory(SL* h)

void SLDestory(SL* h)
{if (h->arr)free(h->arr);h->arr = NULL;h->size = 0;h->capacity = 0;
}

解释：

  • SLDestory 是顺序表的销毁函数，用于释放动态分配的内存资源并重置结构状态，核心目标是避免内存泄漏。
  • 作用：h->arr 是顺序表中存储元素的动态数组（通过 malloc/calloc 分配），free(h->arr) 会将其占用的内存归还给系统。
  • 为什么加 if (h->arr)？
    • 若 h->arr 为 NULL（空表或已释放），free(NULL) 在 C 语言中是安全的（无操作），因此此判断非必需，可简化为直接 free(h->arr)。

结合之前的代码举例：（我写了3个文件）

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
//定义顺序表的结构
typedef int type;
typedef struct Seqlist
{type* arr;//存储数据int size;//有效数据个数int capacity;//空间容量
}SL;
void SLinit(SL* h);
void kuo(SL* h);
void SLpushback(SL* h,type x);
void SLpushfront(SL* h, type x);
void popback(SL* h); 
void popfront(SL* h);
int Find(SL* h, type x);
void SLDestory(SL* h);
void print(SL* h);

//定义顺序表的结构
#include"1.h"
void SLinit(SL* h)
{h->arr = NULL;h->capacity = h->size = 0;
}
void kuo(SL* h)
{if (h->capacity == h->size){int newcapacity = h->capacity == 0 ? 4 : 2 * h->capacity;type* tmp = (type*)realloc(h->arr, sizeof(type) * newcapacity);if (tmp){h->arr = tmp;h->capacity = newcapacity;}else{exit(1);}}
}void SLpushback(SL* h, type x)
{kuo(h);h->arr[h->size++] = x;
}
void SLpushfront(SL* h, type x)
{kuo(h);int i;for (i = h->size; i > 0; i--){h->arr[i] = h->arr[i - 1];}h->arr[i] = x;h->size++;
}
void popback(SL* h)
{assert(h && h->size);h->size--;
}
void popfront(SL* h)
{assert(h && h->size);int i;for (i = 0; i < h->size - 1; i++){h->arr[i] = h->arr[i + 1];}h->size--;
}
int Find(SL* h, type x)
{assert(h);int i;for (i = 0; i < h->size; i++){if (h->arr[i] == x){return i;}}return -1;
}
void SLDestory(SL* h)
{if (h->arr)free(h->arr);h->arr = NULL;h->size = 0;h->capacity = 0;
}
void print(SL* h)
{int i;for (i = 0; i < h->size; i++){printf("%d  ", h->arr[i]);}printf("\n");
}

#include"1.h"
void test1()
{SL h;SLinit(&h);SLpushback(&h, 1);  //1SLpushback(&h, 2);  //12SLpushback(&h, 3);  //123SLpushback(&h, 4);  //1234SLpushfront(&h, 1);  //11234SLpushfront(&h, 2);  //211234SLpushfront(&h, 3);  //3211234SLpushfront(&h, 4);  //43211234print(&h);popback(&h);         //4321123print(&h);popback(&h);         //432112print(&h);popfront(&h);         //32112print(&h);popfront(&h);         //2112print(&h);SLDestory(&h);
}
int main()
{test1();
}

结果为：

​

3.顺序表的指定位置插入

实现指定位置插入，顺序表的指定位置插入是指在数组的第 pos 个下标处插入新元素，核心操作是移动元素 + 赋值，需处理扩容、边界检查等关键步骤，接下来，我将展示代码：

void SLinsert(SL* h, int pos, type x);

//在pos前插入
void SLinsert(SL* h, int pos, type x)
{assert(h);assert(pos >= 0 && pos <= h->size);kuo(h);for (int i = h->size; i > pos; i--){h->arr[i] = h->arr[i - 1];}h->arr[pos] = x;h->size++;
}

讲解：

  • 插入位置 pos 的合法范围应为 [0, size]（含 size），即允许在表尾插入。因此断言应为： 
    assert(pos >= 0 && pos <= h->size);  // 允许在表尾（pos=size）插入

1. 元素移动逻辑

for (int i = h->size; i > pos; i--)  // 从后往前移动元素
{h->arr[i] = h->arr[i - 1];  // 将arr[i-1]的值赋给arr[i]
}
  • 移动方向：从 size 开始到 pos+1，正确（避免数据覆盖）。
  • 示例：若原表为 [1,2,3]（size=3），pos=1 时：
    • i=3：arr[3] = arr[2]（3 → 4号位置）
    • i=2：arr[2] = arr[1]（2 → 3号位置）
    • 结果：[1, _, 2, 3]，pos=1 处空出，可插入新元素。

2. 插入元素与更新 size

h->arr[pos] = x;  // 在pos位置插入新元素（正确）
h->size++;        // 有效元素个数+1（正确）

代码举例：

#include"1.h"
void test1()
{SL h;SLinit(&h);SLpushback(&h, 1);  //1SLpushback(&h, 2);  //12SLpushback(&h, 3);  //123SLpushback(&h, 4);  //1234SLpushfront(&h, 1);  //11234SLpushfront(&h, 2);  //211234SLpushfront(&h, 3);  //3211234SLpushfront(&h, 4);  //43211234print(&h);popback(&h);         //4321123print(&h);popback(&h);         //432112print(&h);popfront(&h);         //32112print(&h);popfront(&h);         //2112print(&h);SLinsert(&h, 2, 55);  //2  1  55  1  2print(&h); SLinsert(&h, 3, 125);  //2  1  55  125  1  2print(&h);SLDestory(&h);
}
int main()
{test1();
}

​

4.顺序表的指定位置删除

顺序表的指定位置删除是指移除数组中第 pos 个下标处的元素，核心操作是移动元素覆盖待删除值。接下来，我将展示该部分的代码以及实现：

void SLerase(SL* h, int pos)

void SLerase(SL* h, int pos)
{assert(h);assert(pos >= 0 && pos < h->size);int i;for (i = pos;i<h->size-1;i++){h->arr[i] = h->arr[i+1];}h->size--;
}

解析：

代码逐行讲解

1. 参数与断言检查
assert(h);  // 确保顺序表指针h非空（必须，避免空指针访问）
assert(pos >= 0 && pos < h->size);  // 检查删除位置pos的合法性
  • pos 合法性：pos 必须在 [0, size-1] 范围内（例如 size=3 时，可删除 0、1、2 位置，不能删除 pos=3）。
  • 隐含检查：pos < h->size 已隐含 size > 0（若 size=0，pos < 0 会触发断言失败），无需额外检查 h->size > 0。
2. 元素前移覆盖（核心逻辑）
for (i = pos; i < h->size - 1; i++)  // 循环条件：i从pos到size-2
{h->arr[i] = h->arr[i + 1];  // 将后一个元素（i+1）覆盖当前元素（i）
}

  • 循环范围：i < h->size - 1 等价于 i <= h->size - 2，即从 pos 移动到倒数第二个元素（size-2）。

    • 示例：若原表为 [1,2,3,4]（size=4），删除 pos=1（值为2）：
      • i=1：arr[1] = arr[2]（3 → 2号位置，表变为 [1,3,3,4]）
      • i=2：arr[2] = arr[3]（4 → 3号位置，表变为 [1,3,4,4]）
      • 循环结束（i=3 时 3 < 4-1 不成立）。

  • 为什么是 size-1？

    • 若 i < h->size（错误条件），当 i = size-1 时，i+1 = size 会访问越界内存（数组最大下标为 size-1）。
    • 原代码 size-1 确保 i+1 最大为 size-1（合法），避免越界。
3. 更新有效元素个数
h->size--;  // 有效元素个数-1（逻辑删除，无需释放内存）
  • 效果：删除后顺序表实际存储的有效元素为前 size-1 个（覆盖后最后一个元素 arr[size-1] 变为无效数据，但不影响访问）。

例：

SLinsert(&h, 3, 125);  //2  1  55  125  1  2
print(&h);
SLerase(&h, 3);
print(&h);             //2  1  55  1  2 将下标为3的删去

5.实现的总代码

本代码，我通过3个文件来实现的，分别为头文件（1.h）、实现文件（1.c）、测试文件(maic.c)

代码如下：

1.h

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
//定义顺序表的结构
typedef int type;
typedef struct Seqlist
{type* arr;//存储数据int size;//有效数据个数int capacity;//空间容量
}SL;
void SLinit(SL* h);
void kuo(SL* h);
void SLpushback(SL* h,type x);
void SLpushfront(SL* h, type x);
void popback(SL* h); 
void popfront(SL* h);
int Find(SL* h, type x);
void SLDestory(SL* h);
void print(SL* h);
void SLinsert(SL* h, int pos, type x);
void SLerase(SL* h, int pos);

1.c

//定义顺序表的结构
#include"1.h"
void SLinit(SL* h)
{h->arr = NULL;h->capacity = h->size = 0;
}
void kuo(SL* h)
{if (h->capacity == h->size){int newcapacity = h->capacity == 0 ? 4 : 2 * h->capacity;type* tmp = (type*)realloc(h->arr, sizeof(type) * newcapacity);if (tmp){h->arr = tmp;h->capacity = newcapacity;}else{exit(1);}}
}void SLpushback(SL* h, type x)
{kuo(h);h->arr[h->size++] = x;
}
void SLpushfront(SL* h, type x)
{kuo(h);int i;for (i = h->size; i > 0; i--){h->arr[i] = h->arr[i - 1];}h->arr[i] = x;h->size++;
}
void popback(SL* h)
{assert(h && h->size);h->size--;
}
void popfront(SL* h)
{assert(h && h->size);int i;for (i = 0; i < h->size - 1; i++){h->arr[i] = h->arr[i + 1];}h->size--;
}
int Find(SL* h, type x)
{assert(h);int i;for (i = 0; i < h->size; i++){if (h->arr[i] == x){return i;}}return -1;
}
void SLDestory(SL* h)
{if (h->arr)free(h->arr);h->arr = NULL;h->size = 0;h->capacity = 0;
}
void print(SL* h)
{int i;for (i = 0; i < h->size; i++){printf("%d  ", h->arr[i]);}printf("\n");
}
//在pos前插入
void SLinsert(SL* h, int pos, type x)
{assert(h);assert(pos >= 0 && pos <= h->size);kuo(h);for (int i = h->size; i > pos; i--){h->arr[i] = h->arr[i - 1];}h->arr[pos] = x;h->size++;
}
void SLerase(SL* h, int pos)
{assert(h);assert(pos >= 0 && pos < h->size);int i;for (i = pos;i<h->size-1;i++){h->arr[i] = h->arr[i+1];}h->size--;
}

main.c

#include"1.h"
void test1()
{SL h;SLinit(&h);SLpushback(&h, 1);  //1SLpushback(&h, 2);  //12SLpushback(&h, 3);  //123SLpushback(&h, 4);  //1234SLpushfront(&h, 1);  //11234SLpushfront(&h, 2);  //211234SLpushfront(&h, 3);  //3211234SLpushfront(&h, 4);  //43211234print(&h);popback(&h);         //4321123print(&h);popback(&h);         //432112print(&h);popfront(&h);         //32112print(&h);popfront(&h);         //2112print(&h);SLinsert(&h, 2, 55);  //2  1  55  1  2print(&h); SLinsert(&h, 3, 125);  //2  1  55  125  1  2print(&h);SLerase(&h, 3);print(&h);             //2  1  55  1  2 将下标为3的删去SLDestory(&h); 
}
int main()
{test1();
}

二、顺序表算法题

根据我们讲解的知识点，我们来看几道关于该知识的算法题：

1.移除元素

27. 移除元素 - 力扣（LeetCode）

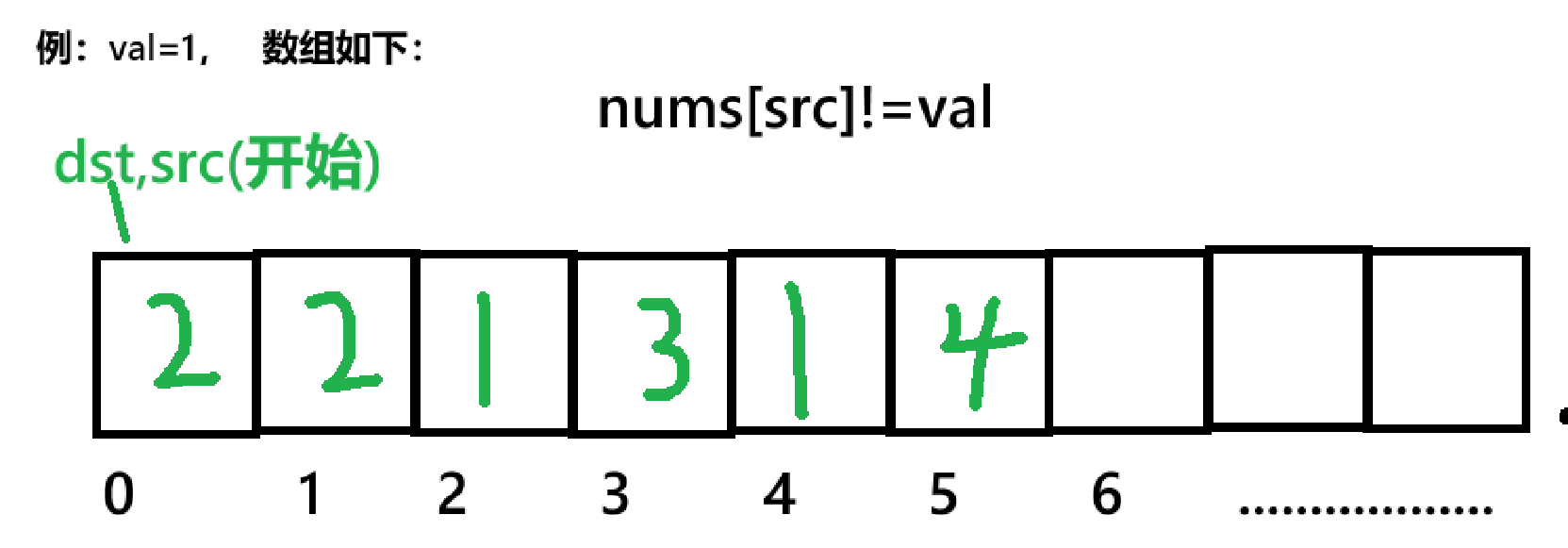
本题思路：我们可以选用双指针法来实现该题，具体操作为：我们在开始时创建两个int变量，src，dst，通过src（数组下标）遍历整个数组，如果发现数组值不为val,我们则将值传入到以dst为下标的数组中，如此情况： 这是简单的讲法，接下来，我将通过代码来讲解：

代码：

int removeElement(int* nums, int numsSize, int val) {int src=0,dst=0;while(src<numsSize){if(nums[src]!=val){nums[dst]=nums[src];dst++;}src++;}return dst;
}

详细讲解：

该算法空间复杂度为 O(1)，时间复杂度为O(n)。

核心逻辑：双指针法

通过两个指针 src（源指针）和 dst（目标指针）遍历数组，将不等于 val 的元素"搬运"到数组前端，覆盖需要移除的元素。

  • src：遍历整个数组，寻找不等于 val 的元素。
  • dst：指向当前需要填充的位置，仅在 src 找到有效元素时移动。
步骤分解
  1. 初始化指针：src = 0，dst = 0（均从数组起始位置开始）。
  2. 遍历数组：src 从 0 到 numsSize-1 循环：
    • 若 nums[src] != val：将 nums[src] 赋值给 nums[dst]，dst 后移一位（指向下一个待填充位置）。
    • 若 nums[src] == val：dst 不动（跳过该元素，后续被覆盖）。
    • 无论是否匹配，src 始终后移一位。
  3. 返回新长度：dst 的值即为移除后有效元素的个数（因为 dst 每填充一个有效元素就 +1）。

2. 删除有序数组中的重复项

26. 删除有序数组中的重复项 - 力扣（LeetCode）

本题思路：我们可以选用双指针法来实现该题，具体操作为：我们在开始时创建两个int变量，src=0，dst=0，通过src（数组下标）遍历整个数组（这一部分与上一题基本相同，但后来操作上有较大不同），如果发现数组值不重复,我们则将值传入到以dst为下标的数组中，忽视掉重复的值，如此情况： 这是简单的讲法，接下来，我将通过代码来讲解：

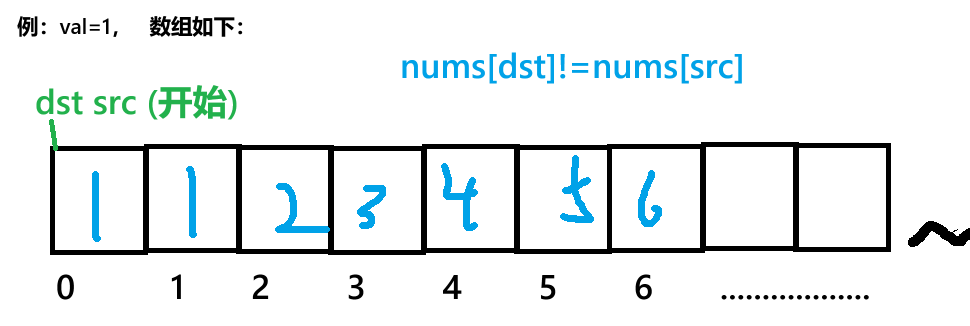
int removeDuplicates(int* nums, int numsSize) {int src=0,dst=0;while(src<numsSize){if(nums[dst]!=nums[src]){nums[++dst]=nums[src];}src++;}return dst+1;
}

详细讲解：

该函数用于移除非严格递增排序数组中的重复元素（只保留一个），返回移除后数组的新长度，空间复杂度为 O(1)（原数组上修改）。

核心逻辑：双指针法（快慢指针）

利用数组已排序的特性，通过两个指针 src（快指针）和 dst（慢指针）遍历数组，仅保留不重复的元素。

  • src：遍历整个数组，寻找与 dst 指向元素不同的新元素。
  • dst：指向当前已确认的不重复元素的最后一个位置，仅在 src 找到新元素时移动。

步骤分解

  1. 初始化指针：src = 0，dst = 0（均从数组起始位置开始）。
  2. 遍历数组：src 从 0 到 numsSize-1 循环：
    • 若 nums[dst] != nums[src]：说明 src 找到新的不重复元素，将 dst 先 +1（移动到下一个待填充位置），再将 nums[src] 赋值给 nums[dst]。
    • 若 nums[dst] == nums[src]：dst 不动（跳过重复元素）。
    • 无论是否重复，src 始终后移一位。
  3. 返回新长度：dst + 1（因为 dst 指向最后一个有效元素的索引，长度需 +1）。

3.合并两个有序数组

88. 合并两个有序数组 - 力扣（LeetCode）

本题思路：题目的要求挺多，注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。此处提示我们要利用好原数组的空间，所以，我们本题的解法围绕着nums1

后解法：三指针法： 创建三个整形指针，例：s1,s2,s3 分别指向：1数组的头，尾部，2数组的尾部，之后再进行操作:

  • 即比较两数组下标s1,s3值对应的大小，nums1[s1] < nums2[s3]：将 nums2[s3] 放入 nums1[s2]，s3 和 s2 均左移一位（s3--，s2--）。
  • 否则：将 nums1[s1] 放入 nums1[s2]，s1 和 s2 均左移一位（s1--，s2--）。
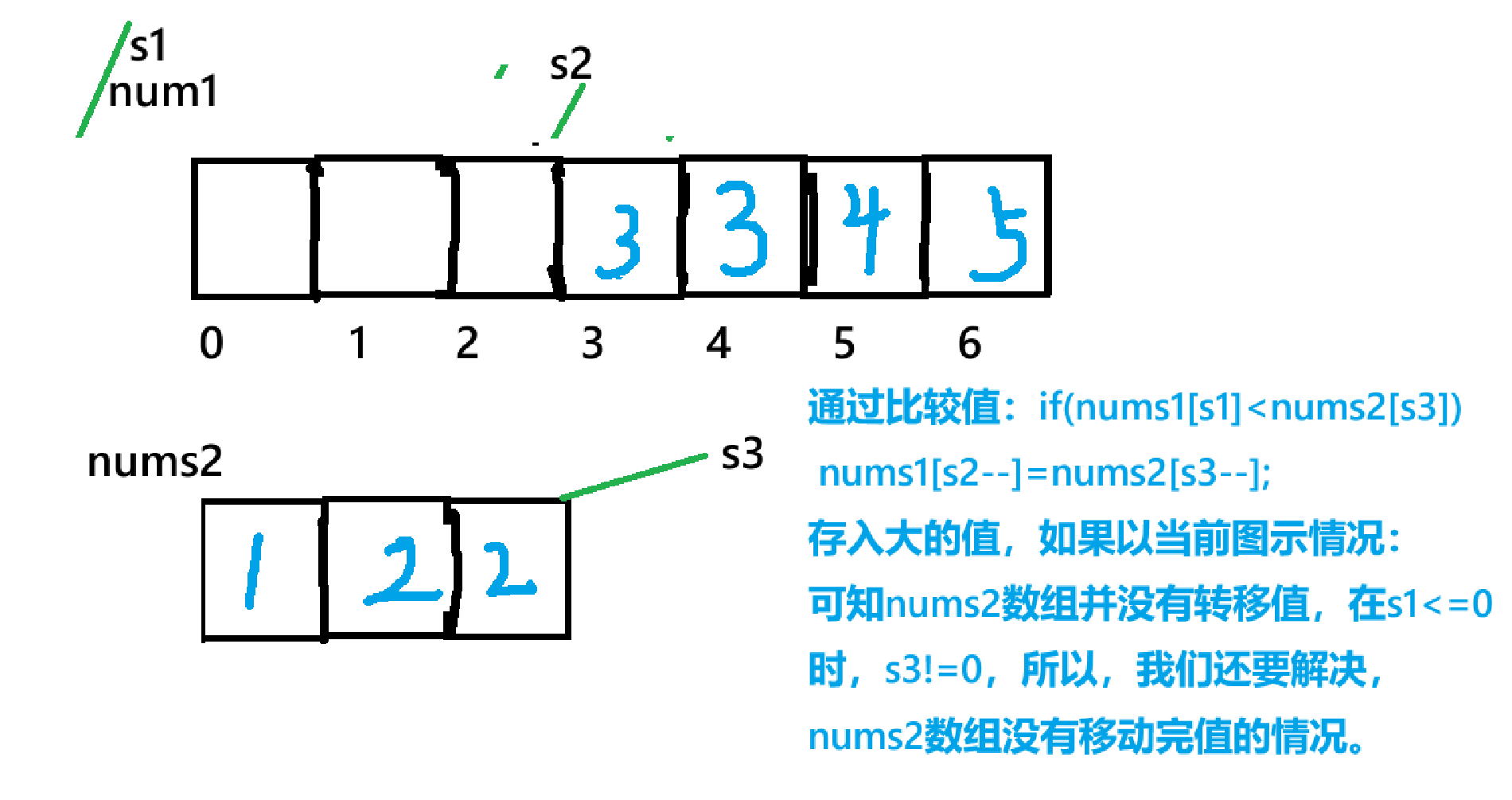
  • 处理剩余元素：若 nums2 仍有未合并的元素（s3 >= 0），直接将剩余元素依次放入 nums1 的头部（此时 nums1 的有效元素已全部合并，s1 已遍历完，s2 指向剩余空位的起始位置）。

具体操作通过代码讲解：

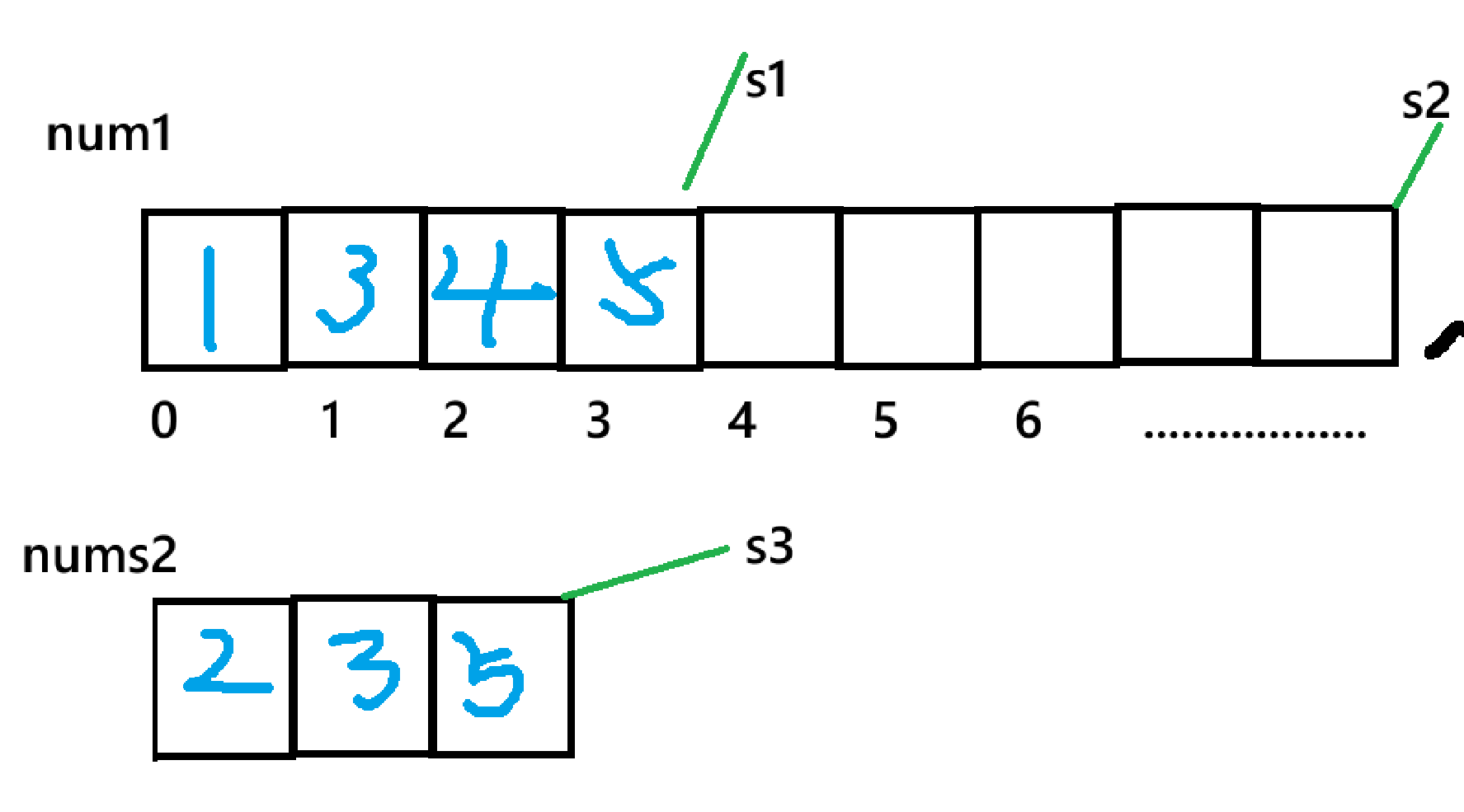
特殊例：

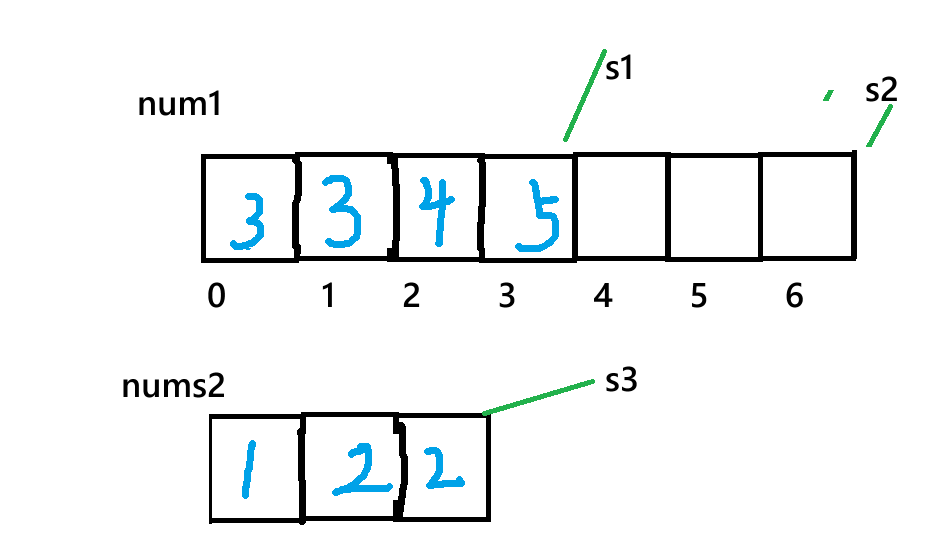
void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) 
{  int s1=m-1;
int s2=n+m-1;
int s3=n-1;
while(s1>=0&&s3>=0)
{if(nums1[s1]<nums2[s3])nums1[s2--]=nums2[s3--];
elsenums1[s2--]=nums1[s1--];
}if(s3>=0){ while(s3>=0){nums1[s2--]=nums2[s3--];}}  
}

总结

  以上就是今天要讲的内容，本篇文章涉及的知识点为：顺序表动态顺序表的实现，顺序表算法题等知识的相关内容，为本章节知识的内容，希望大家能喜欢我的文章，谢谢各位，接下来的内容我会很快更新有关链表的知识。

http://www.dtcms.com/a/523566.html

相关文章：

  • 建设一个网站需要考虑什么海口h5公司
  • 高端广告公司网站建设wordpress插件 stock
  • 第二章、全局配置项目主题色(主题切换+跟随系统)
  • 彻底清理：Vue项目中移除static文件夹的完整指南
  • 【Linux网络】套接字Socket编程预备
  • day18_菜单查询 合并servlet
  • 算法总结篇（枚举-分治）
  • TCP pure ACK 的不可扩展性问题
  • Android16 Wifi打开到自动连接的主要日志过程分析介绍
  • 背包dp——动态规划
  • 找做柜子的网站中国芯片制造最新消息
  • 甘肃省临夏州建设局网站wordpress 未分类
  • 用 Excalidraw+cpolar 做会议协作，像素级还原实体白板体验
  • 使用C++开发Android .so库的优势与实践指南
  • Spring AOP：注解配置与XML配置双实战
  • 基于YOLO11深度学习的半导体晶圆外观缺陷检测系统【Python源码+Pyqt5界面+数据集+安装使用教程+训练代码】【附下载链接】
  • 笔记本电脑待机、睡眠与休眠模式的技术差异解析
  • 2025丨时间很快，又来到1024
  • 基于python人脸识别系统 人脸检测 实时检测 深度学习 Dlib库 ResNet深度卷积神经网络 pyqt设计 大数据（源码）✅
  • 【C + +】unordered_set 和 unordered_map 的用法、区别、性能全解析
  • 《刚刚问世》系列初窥篇-Java+Playwright自动化测试-31- 操作日历时间控件-上篇（详细教程）
  • 电子商城网站建设与维护怎么建设淘客自己的网站_
  • 基于 Vue3 + WebSocket 实现的平板控制端与大屏展示端联动方案
  • 提高自己的网站网站 利润
  • 外贸seo软文发布平台上海百度推广优化排名
  • Qt 图像与定时器实战：实现动态图片轮播效果
  • C++ 模板初阶：从函数重载到泛型编程的优雅过渡
  • 第 01 天：Linux 是什么？内核、发行版及其生态系统
  • Docker 安装 MongoDB 完整指南：从入门到实战
  • Docker 离线安装