梯度下降求解线性回归问题
梯度下降法
梯度下降法有三种方法来求解线性回归问题
-
批量梯度下降法
-
随机梯度下降法
根据是否包含动量能力,随机梯度下降法又包含正常随机梯度下降法及动量随机梯度下降法;
动量随机梯度下降法主要的目的是为了使收敛尽可能跳出局部,找到全局收敛点。 -
小批量随机
代码演示详见gradient_descent.py,该代码包含了批量梯度下降法,随机梯度下降法,小批量随机下降法,动量随机下降法的实现
import numpy as np
import matplotlib.pyplot as plt
import matplotlibmatplotlib.use('TkAgg') # 或 'Agg'# 设置中文字体
plt.rcParams["font.family"] = ["Microsoft YaHei"] # 使用微软雅黑
plt.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题import pandas as pd
from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
import timedef setup_matplotlib_fonts():"""设置 matplotlib 字体以避免警告"""# 方法1: 使用系统字体plt.rcParams['font.family'] = ['DejaVu Sans', 'Microsoft YaHei', 'SimHei', 'Arial Unicode MS']plt.rcParams['axes.unicode_minus'] = False# 方法2: 设置数学字体plt.rcParams['mathtext.fontset'] = 'stix' # 或者 'dejavusans', 'dejavuserif'# 方法3: 检查可用字体available_fonts = sorted([f.name for f in mpl.font_manager.fontManager.ttflist])print("可用的中文字体:", [f for f in available_fonts if 'SimHei' in f or 'Microsoft' in f or 'YaHei' in f])# 选择最佳字体preferred_fonts = ['DejaVu Sans', 'Arial', 'Liberation Sans', 'Microsoft YaHei', 'SimHei']for font in preferred_fonts:if font in available_fonts:plt.rcParams['font.family'] = [font]print(f"使用字体: {font}")breakclass GradientDescentOptimizers:"""梯度下降优化器完整实现"""def __init__(self, learning_rate=0.01, n_iters=1000, fit_intercept=True):self.learning_rate = learning_rateself.n_iters = n_itersself.fit_intercept = fit_interceptdef _add_intercept(self, X):"""添加截距项"""if self.fit_intercept:return np.column_stack([np.ones(X.shape[0]), X])return Xdef _compute_loss(self, X, y, theta):"""计算均方误差损失"""m = X.shape[0]predictions = X @ thetaloss = (1 / (m)) * np.sum((predictions - y) ** 2)return lossdef batch_gradient_descent(self, X, y, verbose=False):"""批量梯度下降 (Batch Gradient Descent)- 每次迭代使用全部训练样本- 收敛稳定但速度慢"""X_b = self._add_intercept(X)m, n = X_b.shapetheta = np.random.randn(n)losses = []thetas_history = [theta.copy()]print("开始批量梯度下降...")start_time = time.time()for i in range(self.n_iters):# 使用全部样本计算梯度predictions = X_b @ thetagradients = (1 / m) * X_b.T @ (predictions - y)# 更新参数theta = theta - self.learning_rate * gradients# 记录损失和参数loss = self._compute_loss(X_b, y, theta)losses.append(loss)thetas_history.append(theta.copy())if verbose and i % 100 == 0:print(f"迭代 {i}: 损失 = {loss:.6f}")training_time = time.time() - start_time# 分离截距和系数if self.fit_intercept:intercept = theta[0]coef = theta[1:]else:intercept = 0.0coef = thetaprint(f"批量梯度下降完成 - 时间: {training_time:.4f}s, 最终损失: {losses[-1]:.6f}")return {'coef': coef,'intercept': intercept,'losses': losses,'thetas_history': thetas_history,'training_time': training_time,'n_iterations': len(losses)}def stochastic_gradient_descent(self, X, y, verbose=False):"""随机梯度下降 (Stochastic Gradient Descent)- 每次迭代使用单个训练样本- 收敛快但不稳定"""X_b = self._add_intercept(X)m, n = X_b.shapetheta = np.random.randn(n)losses = []thetas_history = [theta.copy()]print("开始随机梯度下降...")start_time = time.time()for epoch in range(self.n_iters):epoch_loss = 0# 随机打乱数据indices = np.random.permutation(m)X_shuffled = X_b[indices]y_shuffled = y[indices]for i in range(m):# 使用单个样本xi = X_shuffled[i:i + 1] # 保持2D数组yi = y_shuffled[i:i + 1]# 计算梯度(单个样本)prediction = xi @ thetagradient = xi.T @ (prediction - yi)# 更新参数theta = theta - self.learning_rate * gradient.ravel()# 计算当前样本的损失current_loss = self._compute_loss(xi, yi, theta)epoch_loss += current_loss# 记录平均epoch损失avg_loss = epoch_loss / mlosses.append(avg_loss)thetas_history.append(theta.copy())if verbose and epoch % 100 == 0:print(f"Epoch {epoch}: 平均损失 = {avg_loss:.6f}")training_time = time.time() - start_time# 分离截距和系数if self.fit_intercept:intercept = theta[0]coef = theta[1:]else:intercept = 0.0coef = thetaprint(f"随机梯度下降完成 - 时间: {training_time:.4f}s, 最终损失: {losses[-1]:.6f}")return {'coef': coef,'intercept': intercept,'losses': losses,'thetas_history': thetas_history,'training_time': training_time,'n_iterations': len(losses)}def mini_batch_gradient_descent(self, X, y, batch_size=32, verbose=False):"""小批量梯度下降 (Mini-batch Gradient Descent)- 每次迭代使用一小批训练样本- 平衡了速度和稳定性"""X_b = self._add_intercept(X)m, n = X_b.shapetheta = np.random.randn(n)losses = []thetas_history = [theta.copy()]print(f"开始小批量梯度下降 (batch_size={batch_size})...")start_time = time.time()for epoch in range(self.n_iters):epoch_loss = 0# 随机打乱数据indices = np.random.permutation(m)X_shuffled = X_b[indices]y_shuffled = y[indices]n_batches = 0for i in range(0, m, batch_size):# 使用小批量样本X_batch = X_shuffled[i:i + batch_size]y_batch = y_shuffled[i:i + batch_size]# 计算梯度(小批量)predictions = X_batch @ thetagradients = (1 / len(X_batch)) * X_batch.T @ (predictions - y_batch)# 更新参数theta = theta - self.learning_rate * gradients# 计算当前批次的损失current_loss = self._compute_loss(X_batch, y_batch, theta)epoch_loss += current_lossn_batches += 1# 记录平均epoch损失avg_loss = epoch_loss / n_batches if n_batches > 0 else 0losses.append(avg_loss)thetas_history.append(theta.copy())if verbose and epoch % 100 == 0:print(f"Epoch {epoch}: 平均损失 = {avg_loss:.6f}")training_time = time.time() - start_time# 分离截距和系数if self.fit_intercept:intercept = theta[0]coef = theta[1:]else:intercept = 0.0coef = thetaprint(f"小批量梯度下降完成 - 时间: {training_time:.4f}s, 最终损失: {losses[-1]:.6f}")return {'coef': coef,'intercept': intercept,'losses': losses,'thetas_history': thetas_history,'training_time': training_time,'n_iterations': len(losses),'batch_size': batch_size}def predict(self, X, coef, intercept):"""预测函数"""if self.fit_intercept:return X @ coef + interceptelse:return X @ coef# 完整的对比演示
def comprehensive_comparison(X_train, X_test, y_train, y_test):"""完整的梯度下降方法对比"""# 数据标准化scaler = StandardScaler()X_train_scaled = scaler.fit_transform(X_train)X_test_scaled = scaler.transform(X_test)y_train_scaled = (y_train - y_train.mean()) / y_train.std()y_test_scaled = (y_test - y_test.mean()) / y_test.std()# 创建优化器optimizer = GradientDescentOptimizers(learning_rate=0.01, n_iters=500)# 运行三种算法print("=" * 60)print("梯度下降算法对比实验")print("=" * 60)results = {}# 批量梯度下降results['BGD'] = optimizer.batch_gradient_descent(X_train_scaled, y_train_scaled)# 随机梯度下降results['SGD'] = optimizer.stochastic_gradient_descent(X_train_scaled, y_train_scaled)# 小批量梯度下降(不同batch size)batch_sizes = [16, 32, 64]for bs in batch_sizes:results[f'MBGD_{bs}'] = optimizer.mini_batch_gradient_descent(X_train_scaled, y_train_scaled, batch_size=bs)# 测试集评估print("\n" + "=" * 60)print("测试集性能评估")print("=" * 60)for name, result in results.items():y_pred = optimizer.predict(X_test_scaled, result['coef'], result['intercept'])mse = mean_squared_error(y_test_scaled, y_pred)r2 = r2_score(y_test_scaled, y_pred)result['test_mse'] = mseresult['test_r2'] = r2print(f"{name:10} | 训练时间: {result['training_time']:6.3f}s | "f"测试MSE: {mse:.6f} | 测试R²: {r2:.4f}")return optimizer, results, X_train_scaled, X_test_scaled, y_train_scaled, y_test_scaleddef visualization_analysis(results, X_train, y_train):"""可视化分析结果"""plt.figure(figsize=(20, 12))# 1. 损失曲线对比plt.subplot(2, 3, 1)colors = {'BGD': 'blue', 'SGD': 'red', 'MBGD_16': 'green', 'MBGD_32': 'orange', 'MBGD_64': 'purple'}for name, result in results.items():color = colors.get(name, 'gray')plt.plot(result['losses'], label=name, color=color, alpha=0.8)plt.xlabel('迭代次数/Epoch')plt.ylabel('损失')plt.title('损失曲线对比')plt.legend()plt.yscale('log')plt.grid(True, alpha=0.3)# 2. 训练时间比较plt.subplot(2, 3, 2)names = list(results.keys())times = [results[name]['training_time'] for name in names]plt.bar(names, times, color=[colors.get(name, 'gray') for name in names], alpha=0.7)plt.ylabel('训练时间 (秒)')plt.title('训练时间比较')plt.xticks(rotation=45)plt.grid(True, alpha=0.3)# 3. 测试集性能比较plt.subplot(2, 3, 3)mse_scores = [results[name]['test_mse'] for name in names]r2_scores = [results[name]['test_r2'] for name in names]x = np.arange(len(names))width = 0.35plt.bar(x - width / 2, mse_scores, width, label='MSE', alpha=0.7)plt.bar(x + width / 2, r2_scores, width, label='R²', alpha=0.7)plt.xlabel('算法')plt.ylabel('分数')plt.title('测试集性能比较')plt.xticks(x, names, rotation=45)plt.legend()plt.grid(True, alpha=0.3)# 4. 参数空间轨迹(前两个特征)if X_train.shape[1] >= 2:plt.subplot(2, 3, 4)# 创建损失函数的等高线theta0_vals = np.linspace(-2, 2, 50)theta1_vals = np.linspace(-2, 2, 50)loss_vals = np.zeros((len(theta0_vals), len(theta1_vals)))X_b = optimizer._add_intercept(X_train)sample_indices = np.random.choice(X_b.shape[0], 100, replace=False) # 采样加速计算X_sample = X_b[sample_indices]y_sample = y_train[sample_indices]for i, t0 in enumerate(theta0_vals):for j, t1 in enumerate(theta1_vals):theta_temp = np.array([t0, t1] + [0] * (X_b.shape[1] - 2)) # 只考虑前两个参数loss_vals[i, j] = optimizer._compute_loss(X_sample, y_sample, theta_temp)plt.contour(theta1_vals, theta0_vals, loss_vals, levels=20, alpha=0.5)# 绘制轨迹(只显示前100步避免过于密集)for name, result in results.items():if len(result['thetas_history']) > 0:thetas_arr = np.array(result['thetas_history'])color = colors.get(name, 'gray')# 只显示前两个参数的轨迹plt.plot(thetas_arr[:100, 1], thetas_arr[:100, 0], 'o-',markersize=2, label=name, color=color, alpha=0.7, linewidth=1)plt.xlabel('θ₁ (系数1)')plt.ylabel('θ₀ (截距)')plt.title('参数空间优化路径 (前100步)')plt.legend()plt.grid(True, alpha=0.3)# 5. 收敛速度细节(前50次迭代)plt.subplot(2, 3, 5)for name, result in results.items():color = colors.get(name, 'gray')losses = result['losses'][:50] # 只显示前50次迭代plt.plot(losses, label=name, color=color, alpha=0.8)plt.xlabel('迭代次数')plt.ylabel('损失')plt.title('前期收敛速度')plt.legend()plt.yscale('log')plt.grid(True, alpha=0.3)# 6. 最终系数比较plt.subplot(2, 3, 6)n_features = len(results['BGD']['coef'])x_pos = np.arange(n_features)width = 0.15for i, (name, result) in enumerate(results.items()):if 'coef' in result:offset = width * (i - len(results) / 2)plt.bar(x_pos + offset, result['coef'], width, label=name, alpha=0.7)plt.xlabel('特征索引')plt.ylabel('系数值')plt.title('最终系数比较')plt.legend()plt.grid(True, alpha=0.3)plt.tight_layout()plt.show()class AdvancedGradientDescent(GradientDescentOptimizers):"""高级梯度下降:学习率动态调度和动量"""def __init__(self, learning_rate=0.01, n_iters=1000, momentum=0.9,lr_schedule='constant', decay_rate=0.1):super().__init__(learning_rate, n_iters)self.momentum = momentumself.lr_schedule = lr_scheduleself.decay_rate = decay_ratedef _get_learning_rate(self, iteration):"""动态学习率"""if self.lr_schedule == 'constant':# 常量,不衰减return self.learning_rateelif self.lr_schedule == 'time_based':# 按照底数方式衰减return self.learning_rate / (1 + self.decay_rate * iteration)elif self.lr_schedule == 'exponential':# 自然指数方式衰减return self.learning_rate * np.exp(-self.decay_rate * iteration)elif self.lr_schedule == 'step':# 步长方式进行衰减return self.learning_rate * (0.5 ** (iteration // 100))else:return self.learning_ratedef sgd_with_momentum(self, X, y, verbose=False):"""带动量的随机梯度下降"""X_b = self._add_intercept(X)m, n = X_b.shapetheta = np.random.randn(n)velocity = np.zeros(n) # 动量项losses = []learning_rates = []print("开始带动量的SGD...")start_time = time.time()for epoch in range(self.n_iters):current_lr = self._get_learning_rate(epoch)learning_rates.append(current_lr)epoch_loss = 0indices = np.random.permutation(m)X_shuffled = X_b[indices]y_shuffled = y[indices]for i in range(m):xi = X_shuffled[i:i + 1]yi = y_shuffled[i:i + 1]# 计算梯度prediction = xi @ thetagradient = xi.T @ (prediction - yi)# 动量更新velocity = self.momentum * velocity + current_lr * gradient.ravel()theta = theta - velocitycurrent_loss = self._compute_loss(xi, yi, theta)epoch_loss += current_lossavg_loss = epoch_loss / mlosses.append(avg_loss)if verbose and epoch % 100 == 0:print(f"Epoch {epoch}: 损失 = {avg_loss:.6f}, 学习率 = {current_lr:.6f}")training_time = time.time() - start_timeif self.fit_intercept:intercept = theta[0]coef = theta[1:]else:intercept = 0.0coef = thetaprint(f"带动量SGD完成 - 时间: {training_time:.4f}s, 最终损失: {losses[-1]:.6f}")return {'coef': coef,'intercept': intercept,'losses': losses,'learning_rates': learning_rates,'training_time': training_time,'n_iterations': len(losses)}def advanced_optimizers_demo(X, y):"""高级优化器演示"""# 生成数据# X, y = make_regression(n_samples=500, n_features=3, noise=0.1, random_state=42)scaler = StandardScaler()X_scaled = scaler.fit_transform(X)y_scaled = (y - y.mean()) / y.std()# 测试不同配置configurations = {'SGD_常量学习率': {'momentum': 0.0, 'lr_schedule': 'constant'},'SGD_指数衰减': {'momentum': 0.0, 'lr_schedule': 'exponential', 'decay_rate': 0.01},'动量SGD_常量': {'momentum': 0.1, 'lr_schedule': 'constant'},'动量SGD_时间衰减': {'momentum': 0.1, 'lr_schedule': 'time_based', 'decay_rate': 0.01}}advanced_results = {}for name, config in configurations.items():print(f"\n训练 {name}...")advanced_optimizer = AdvancedGradientDescent(learning_rate=0.1,n_iters=200,**config)advanced_results[name] = advanced_optimizer.sgd_with_momentum(X_scaled, y_scaled)# 可视化比较plt.figure(figsize=(15, 10))# 损失曲线plt.subplot(2, 2, 1)for name, result in advanced_results.items():plt.plot(result['losses'], label=name, alpha=0.8)plt.xlabel('Epoch')plt.ylabel('损失')plt.title('高级优化器损失曲线')plt.legend()plt.yscale('log')plt.grid(True, alpha=0.3)# 学习率变化plt.subplot(2, 2, 2)for name, result in advanced_results.items():if 'learning_rates' in result:plt.plot(result['learning_rates'], label=name, alpha=0.8)plt.xlabel('Epoch')plt.ylabel('学习率')plt.title('学习率调度')plt.legend()plt.grid(True, alpha=0.3)# 收敛速度比较(前50个epoch)plt.subplot(2, 2, 3)for name, result in advanced_results.items():plt.plot(result['losses'][:50], label=name, alpha=0.8)plt.xlabel('Epoch')plt.ylabel('损失')plt.title('前期收敛速度')plt.legend()plt.yscale('log')plt.grid(True, alpha=0.3)# 训练时间比较plt.subplot(2, 2, 4)names = list(advanced_results.keys())times = [advanced_results[name]['training_time'] for name in names]plt.bar(names, times, alpha=0.7)plt.ylabel('训练时间 (秒)')plt.title('训练时间比较')plt.xticks(rotation=45)plt.grid(True, alpha=0.3)plt.tight_layout()plt.show()return advanced_resultsdef momentum_physical_analogy():"""动量物理类比演示"""# 模拟小球在山谷中的运动def loss_landscape(x):"""损失函数地形 - 有多个局部最小值的复杂地形"""return 0.1 * x ** 4 - 2 * x ** 2 + 0.5 * x ** 3 - 0.3 * x + 10def gradient(x):"""梯度函数"""return 0.4 * x ** 3 - 4 * x + 1.5 * x ** 2 - 0.3# 参数learning_rate = 0.01momentum = 0.9n_iterations = 200# 无动量优化x_no_momentum = 4.0 # 初始位置velocity_no_momentum = 0path_no_momentum = [x_no_momentum]# 带动量优化x_with_momentum = 4.0velocity_with_momentum = 0path_with_momentum = [x_with_momentum]for i in range(n_iterations):# 无动量grad_no_momentum = gradient(x_no_momentum)x_no_momentum = x_no_momentum - learning_rate * grad_no_momentumpath_no_momentum.append(x_no_momentum)# 带动量grad_with_momentum = gradient(x_with_momentum)velocity_with_momentum = momentum * velocity_with_momentum + learning_rate * grad_with_momentumx_with_momentum = x_with_momentum - velocity_with_momentumpath_with_momentum.append(x_with_momentum)# 可视化x_vals = np.linspace(-3, 5, 100)y_vals = loss_landscape(x_vals)plt.figure(figsize=(15, 5))plt.subplot(1, 2, 1)plt.plot(x_vals, y_vals, 'b-', label='损失函数地形', linewidth=2)plt.plot(path_no_momentum, [loss_landscape(x) for x in path_no_momentum],'ro-', markersize=4, label='无动量路径', alpha=0.7)plt.plot(path_with_momentum, [loss_landscape(x) for x in path_with_momentum],'go-', markersize=4, label='带动量路径', alpha=0.7)plt.xlabel('参数 x')plt.ylabel('损失值')plt.title('优化路径对比')plt.legend()plt.grid(True, alpha=0.3)plt.subplot(1, 2, 2)plt.plot(range(len(path_no_momentum)), path_no_momentum, 'r-', label='无动量', linewidth=2)plt.plot(range(len(path_with_momentum)), path_with_momentum, 'g-', label='带动量', linewidth=2)plt.xlabel('迭代次数')plt.ylabel('参数值')plt.title('参数更新轨迹')plt.legend()plt.grid(True, alpha=0.3)plt.tight_layout()plt.show()print("优化结果:")print(f"无动量 - 最终位置: {path_no_momentum[-1]:.4f}, 最终损失: {loss_landscape(path_no_momentum[-1]):.4f}")print(f"带动量 - 最终位置: {path_with_momentum[-1]:.4f}, 最终损失: {loss_landscape(path_with_momentum[-1]):.4f}")if __name__ == '__main__':# momentum_physical_analogy()# 加载数据df = pd.read_csv('resources/realistic_linear_regression_dataset.csv', header=0)X = df[["ProductionCost", "MarketingSpend", "SeasonalDemandIndex", "CompetitorPrice", "CustomerRating","StoreCount"]]y = df["SalesRevenue"]# 指定测试集比例X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)X_train = X_train.valuesy_train = y_train.valuesX_test = X_test.valuesy_test = y_test.values# 模型训练, 运行完整对比optimizer, results, X_train, X_test, y_train, y_test = comprehensive_comparison(X_train, X_test, y_train, y_test)# 运行可视化visualization_analysis(results, X_train, y_train)# 运行高级优化器演示advanced_results = advanced_optimizers_demo(X_train, y_train)
上诉训练使用的测试数据见:
数据集:linear_regression_dataset
运行结果见:
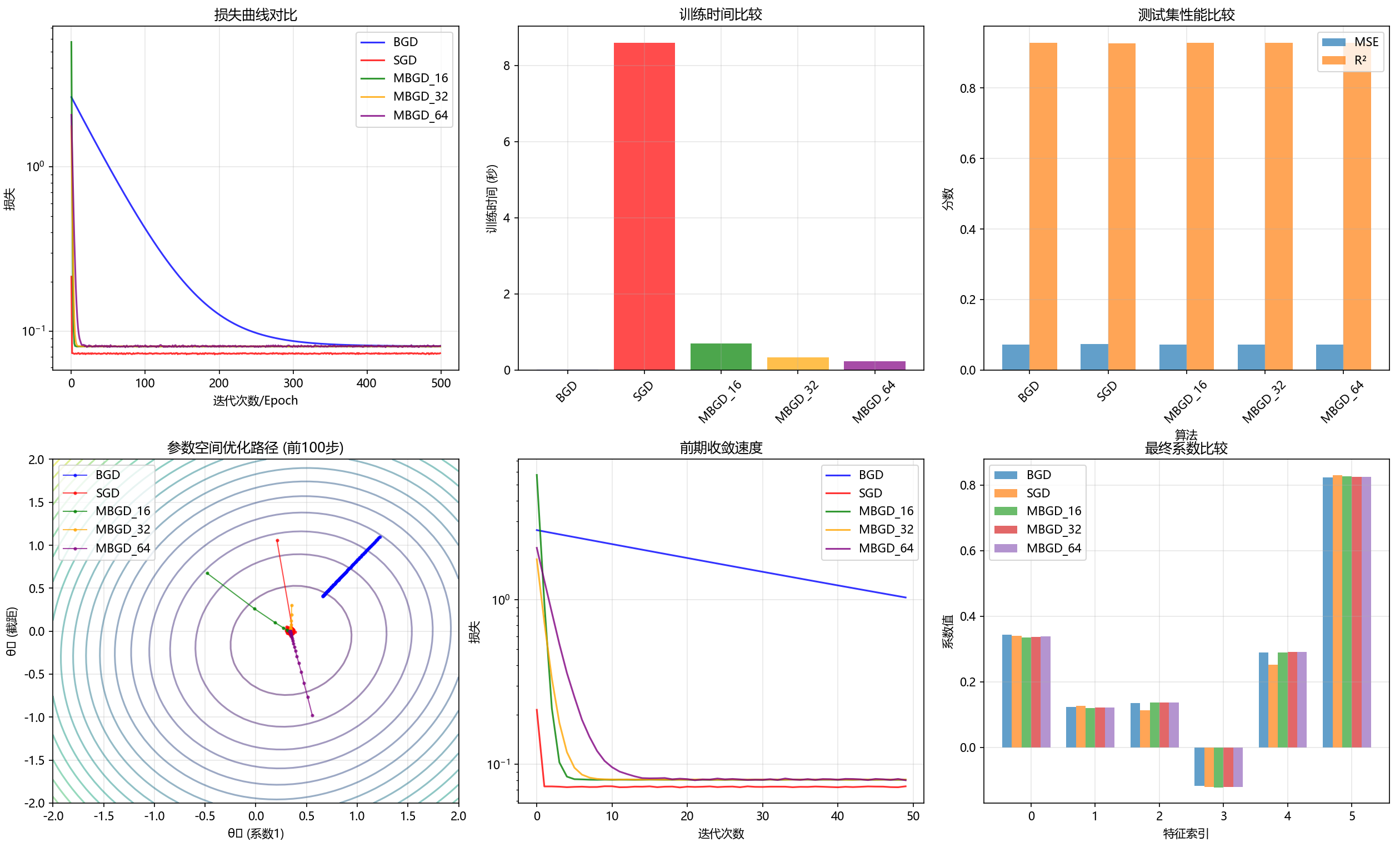
下图为批量梯度,随机梯度,小批量梯度算法的表现与区别
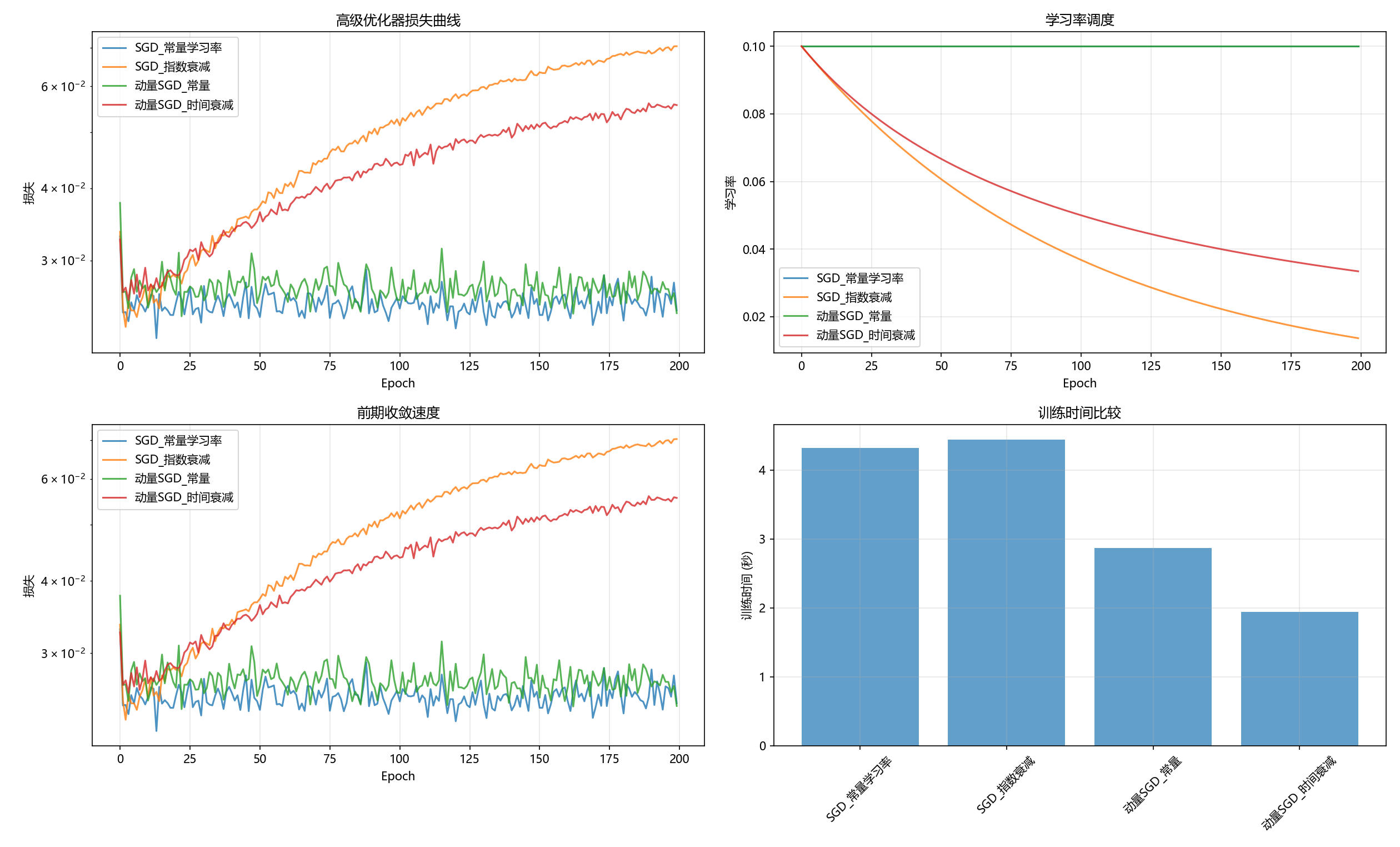
下图为带有动量的随机梯度下降法的表现与区别