矩阵题型hot100
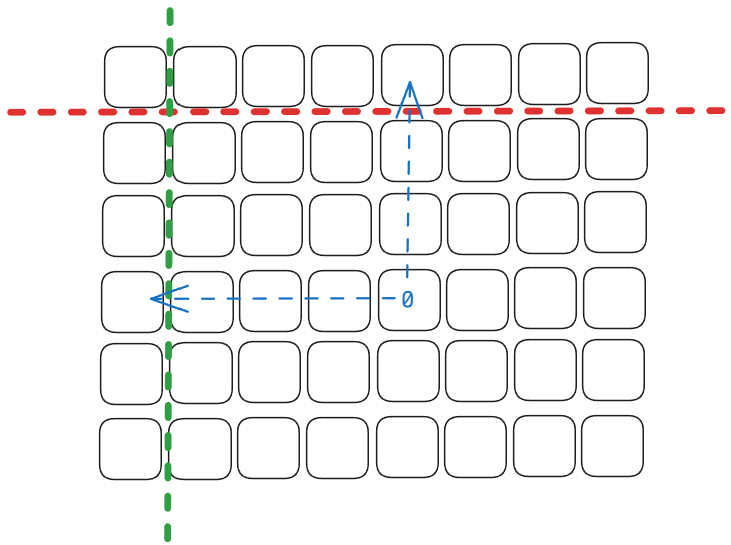
73.矩阵置零
思路:
- 方法一:开拓一个空间,对原矩阵进行遍历并记录那些元素为0的坐标(i,j);随后再遍历一遍矩阵,根据元素为0的坐标(i,j)的 第i行和第j列进行置0.
- 方法二:延续方法一进行优化,我们可以不开拓一个空间去存储这些坐标,而是将这些坐标值反应到第一行和第一列的坐标下,后续通过判断第一行和第一列,来对指定位置行和列进行置0操作。
- 注意:方法二只能是针对矩阵中非第一行和非第一列元素的判断;如果第一行和第一列需要置0的话则需要先进行判断,在最后才对第一行和第一列置0。
- 如果不这样做的话,在判断到第一行和第一列时就对第一行和第一列置0了,此时还有些需要置0的坐标被覆盖了,导致没置0完全。
Code
class Solution:def setZeroes(self, matrix: List[List[int]]) -> None:"""Do not return anything, modify matrix in-place instead."""### 方法一:O(m+n)# mark = []# for i in range(len(matrix)):# for j in range(len(matrix[0])):# if matrix[i][j] == 0:# mark.append((i,j)) ## 遍历矩阵,统计哪些位置出现0# for x, y in mark:# self.set_zero(matrix, x, y)### 方法二:能否将要置0的行index和列index放在原矩阵中,这样就避免了开拓空间去存储这个信息row_flag, line_flag = False, Falsefor i in range(len(matrix)): ## 针对第一列if matrix[i][0] == 0:line_flag = Truefor j in range(len(matrix[0])): ## 针对第一行if matrix[0][j] == 0:row_flag = True##### 不针对第一行和第一列时的操作;因为如果第一行和第一列本身也有0,那么会将整一行和整一列都置为0,导致了后续整个矩阵都被置为0for i in range(1, len(matrix)):for j in range(1, len(matrix[0])):if matrix[i][j] == 0:matrix[i][0] = 0 ## 第i行 和 第j列 需要置0matrix[0][j] = 0for row in range(1, len(matrix)): ## 遍历第一列,需要对行置0操作if matrix[row][0] == 0:for j in range(len(matrix[0])): ## 将row的这一行置0matrix[row][j] = 0for line in range(1, len(matrix[0])): ## 遍历第一行,需要对列置0操作if matrix[0][line] == 0:for i in range(len(matrix)):matrix[i][line] = 0 ## 将line的这一行置0# if row_flag or line_flag: ## 证明第一行和第一列本身有0if row_flag: ## 第一行需要置0for i in range(len(matrix[0])):matrix[0][i] = 0if line_flag: ### 第一列需要置0for j in range(len(matrix)):matrix[j][0] = 054.螺旋矩阵
思路:
维护好两个指针去进行遍历操作
方法一、模拟法(通用)
Code
class Solution:def spiralOrder(self, matrix: List[List[int]]) -> List[int]:row, line = len(matrix), len(matrix[0])result_num = row * lineresult = []visited = [[False] * line for _ in range(row)] ### 记录遍历过的元素start_x, start_y = 0, 0directions = [[0,1],[1,0],[0,-1],[-1,0]] ### 遍历的方向direction_index = 0while len(result) != result_num:result.append(matrix[start_x][start_y])visited[start_x][start_y] = Truenext_x, next_y = start_x + directions[direction_index][0], start_y + directions[direction_index][1]if not (0 <= next_x < row) or not (0 <= next_y < line) or visited[next_x][next_y]:direction_index = (direction_index + 1) % 4start_x, start_y = start_x + directions[direction_index][0], start_y + directions[direction_index][1]return result
59. 螺旋矩阵Ⅱ
方式一:模拟法
Code
class Solution:def generateMatrix(self, n: int) -> List[List[int]]:matrix = [[0] * n for _ in range(n)]start_x, start_y = 0, 0visited = [[False] * n for _ in range(n)]directions = [[0,1], [1,0], [0,-1], [-1,0]]directions_index = 0count = 1while count <= n**2:matrix[start_x][start_y] = count count += 1visited[start_x][start_y] = Truenext_x, next_y = start_x + directions[directions_index][0], start_y + directions[directions_index][1]if not (0 <= next_x < n) or not (0 <= next_y < n) or matrix[next_x][next_y]:directions_index = (directions_index + 1) % 4start_x, start_y = start_x + directions[directions_index][0], start_y + directions[directions_index][1]return matrix方式二:针对方阵的实现
Code
class Solution:def generateMatrix(self, n: int) -> List[List[int]]:matrix = [[0] * n for _ in range(n)]row, line = len(matrix), len(matrix[0])start_x, start_y = 0, 0row_offset, line_offset = 0, 0count = 1loop, mid = n//2, n//2for _ in range(loop): ## 进行loop圈循环for _ in range(line_offset, line-1-line_offset): ## 遍历第一行的列 右matrix[start_x][start_y] = countstart_y += 1count += 1for _ in range(row_offset, row-1-row_offset): ## 遍历每一列的行 下matrix[start_x][start_y] = countstart_x += 1count += 1 for _ in range(line-1-line_offset, line_offset, -1): ## 逆向遍历 左matrix[start_x][start_y] = countstart_y -= 1count += 1for _ in range(row-1-row_offset, row_offset, -1): ## 逆向遍历 上matrix[start_x][start_y] = countstart_x -= 1count += 1row_offset += 1line_offset += 1start_x += 1 ### 这里如果不都+1的话是回到当前外层循环的起点,需要都+1才能到内层循环的起点start_y += 1#### 如果是偶数的话,遍历loop后矩阵就得到了### 如果是奇数的话,需要手动设置中心点if n % 2 == 1:matrix[mid][mid] = countreturn matrix48. 旋转矩阵
矩阵顺时针旋转90度
思路:
- 先转置再翻转
- 顺时针旋转90度的坐标变换为 (i, j) → (j, n-1-i)
- 转置实现(i, j) → (j, i),水平翻转实现 (j, i)
→(j, n-1-i)
Code
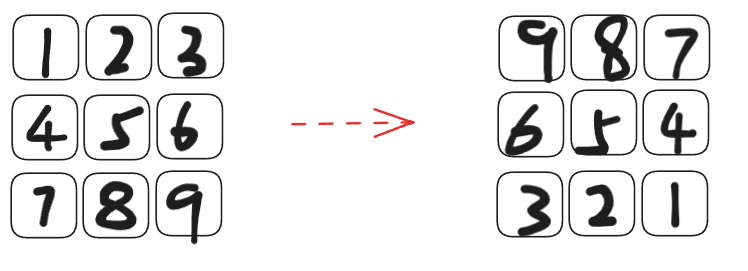
class Solution:def rotate(self, matrix: List[List[int]]) -> None:"""Do not return anything, modify matrix in-place instead."""### 实现转置+翻转row = line = len(matrix)for i in range(row):for j in range(i, line):matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]for i in range(row):matrix[i] = matrix[i][::-1]矩阵旋转180度
思路:
- 先对每一行的数组进行翻转,随后对每一行进行翻转。(翻转两次)
240.搜索二维矩阵Ⅱ
思路:
- 利用矩阵从左向右和从上到下是递增的。
- 如何找到一个点,其方向一个是递增,一个是递减,那从这点就可以去定向去target的所处范围。
Code
class Solution:def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:row, line = len(matrix), len(matrix[0])### 从左下角 / 右上角开始进行z形查找。### 因为这两个位置的方向的数字变化方向相反,可以根据这个特点来利用### 而左上角,向下和 向左都是增大。右下角,向左和向上都是减少cur_x, cur_y = 0, line-1while ( 0 <= cur_x < row) and ( 0 <= cur_y < line): ## 确保坐标有效 cur_value = matrix[cur_x][cur_y]if cur_value > target:cur_y -= 1 ## 往小的方向elif cur_value < target:cur_x += 1 ## 往大的方向else:return True### 跳出循环时,索引越界,证明在矩阵中不存在targetreturn False