数据结构——三十、图的深度优先遍历(DFS)(王道408)
文章目录
- 前言
- 一.与树的深度优先遍历之间的联系
- 1.树的深度优先遍历
- 1.树的先根遍历
- 2.图的深度优先遍历
- 1.代码思路
- 2.代码展示
- 3.代码过程
- 4.代码缺陷
- 5.改良
- 1.代码展示
- 二.复杂度分析
- 1.空间复杂度
- 1.最坏空间复杂度
- 2.最好空间复杂度
- 2.时间复杂度
- 1.邻接矩阵存储的图
- 2.邻接表存储的图
- 三.深度优先遍历序列
- 1.学会按照代码的思路手搓广度优先遍历序列
- 2.遍历序列的可变性
- 3.结论
- 四.深度优先生成树
- 1.获得深度优先生成树的过程
- 2.结论
- 五.深度优先生成森林
- 六.图的遍历与图的连通性
- 1.无向图
- 2.有向图
- 七.知识回顾与重要考点
- 结语
前言
本文探讨了图与树的深度优先遍历(DFS)之间的联系。树的先根遍历从根节点出发,依次访问其子树;而图的DFS在此基础上增加了访问标记数组,防止重复访问。通过递归算法实现:从起始顶点v出发,访问v并标记为已访问,然后依次检查v的邻接顶点w,若w未被访问则递归调用DFS。以具体图示为例,详细展示了从顶点2出发的DFS调用栈和访问标记的变化过程,验证了该算法的正确性。DFS与树的先根遍历逻辑相似,主要区别在于图需要处理顶点可能被多次访问的情况。
代码在文章开头(虽然名字写的是图的广度优先遍历,但是其实是写在一起了),需要自取🧐
一.与树的深度优先遍历之间的联系
1.树的深度优先遍历
1.树的先根遍历
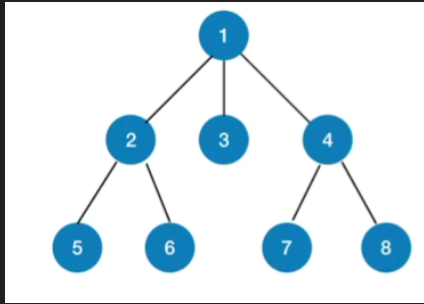
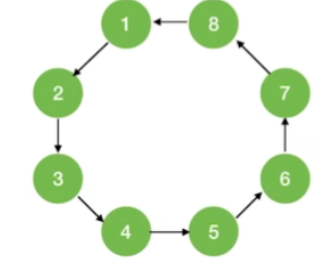
- 先访问1号结点
- 再访问1号结点的第一个子树,也就是2号结点
- 再访问2号结点的第一个子树,也就是5号节点
- 5号节点的下面已经没有子树了
- 所以会跳出这一层的递归回到2号节点
- 对于2号节点,它还有一个没有访问的子树也就是6号节点
- 所以接下来访问6号节点
- 后面的操作与之前类似,不做赘述
- 最终,先根遍历序列:1,2,5,6,3,4,7,8
新找到的相邻结点一定是没有访问过的,这与图不一样
2.图的深度优先遍历
1.代码思路
- 我们也需要设置这样的一个数组,用来标记每一个顶点是否曾经被访问过
- 那其实图的深度优先遍历算法和树的先根遍历是很类似的
- 都是先访问一个节点,然后再用一个循环来依次检查和这个节点相邻的其他节点,然后再进行更深一层的访问
- 只不过对图的深度优先遍历,我们增加了这样的一个数组而已
2.代码展示
bool visited [MAXVertexNUM]; //访问标记数组
void DFS(Graph G,int v){ //从顶点v出发,深度优先遍历图Gvisit(v); //访问顶点vvisited[v]=TRUE;//设已访问标记for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w))if(visited[w]){//w为u的尚未访问的邻接顶点DFS(G,w);}// if\
}

3.代码过程
-
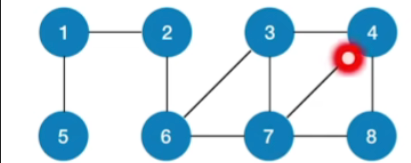
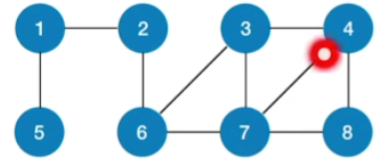
假设我们是要从2号节点出发,对这个图进行深度优先遍历,所以刚开始调用的DFS函数,传入的这个v的值应该是2

-
那我们首先会访问2号节点,接下来会把与之对应的这个visit值设为true

-
然后这个for循环做的事情是要检查和2号节点相邻的1和6这两个顶点,但是和它相邻的第一个顶点应该是1号顶点,而1号顶点此时没有被访问过,因此下一层的这个DFS函数,我们传入的这个参数应该是1

-
那在1号顶点的这层DFS函数当中,我们会访问1号顶点,并且把他的visit值设为true

-
接下来要检查和1号顶点相邻的其他的顶点,那和1号相邻的第一个顶点是2号,但是由于2号顶点的visit值等于true,也就是这个if条件不满足,因此2号顶点会被跳过
-
那接下来找到的下一个和1号相连接的顶点就应该是5号顶点,所以下一层的DFS函数传入的参数应该是5
-
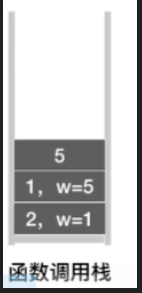
访问5号顶点,设置其visit值为true

-
由于和5号顶点相邻的所有顶点都被访问过,所以5号顶点的这个for循环什么也不会做
-
那这个顶点的DFS函数执行完了之后,就会返回上一层的递归调用,也就是1号顶点这一层
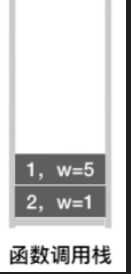
-
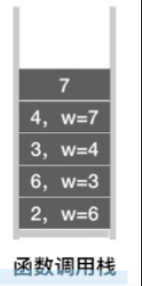
接下来的操作类似,后面只放出递归调用栈与visit值的变化过程

-
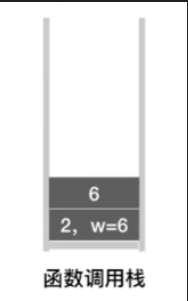
-

-
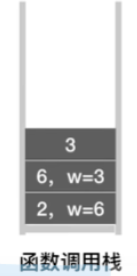
-

-
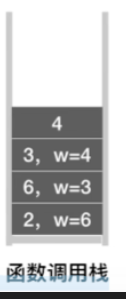
-

-
-

-

-

-
由于所有的元素已经被访问,因此逐层递归压入函数栈的函数,直至栈为空

4.代码缺陷
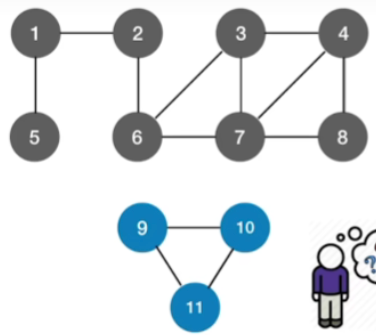
- 如果是非连通图,则无法遍历完所有结点
5.改良
1.代码展示
bool visited [MAXVertexNUM]; //访问标记数组
void DFSTraverse(Graph G){//对图G进行深度优先遍历for(v=0;v<G.vexnum++v)visited[v]=FALSE;//初始化已访问标记数据for(v=0;v<G.vexnum++v)//本代码中是从v=0开始遍历if(visited[v])DFS(G,v);
}
void DFS(Graph G,int v){ //从顶点v出发,深度优先遍历图Gvisit(v); //访问顶点vvisited[v]=TRUE;//设已访问标记for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w))if(visited[w]){//w为v的尚未访问的邻接顶点DFS(G,w);}// if\
}
- 如果在visit数组当中发现了有某一个元素,它的visit值依然是false,那么就说明与之相对应的顶点是没有被访问过的,那我们再从这个顶点出发再调用一次DFS函数就可以了
二.复杂度分析
1.空间复杂度
1.最坏空间复杂度

- 空间复杂度:来自函数调用栈,最坏情况,递归深度为O(W)
2.最好空间复杂度
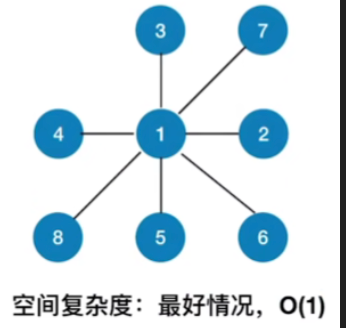
- 空间复杂度:最好情况,O(1)
2.时间复杂度
时间复杂度=访问各结点所需时间+探索各条边所需时间
1.邻接矩阵存储的图
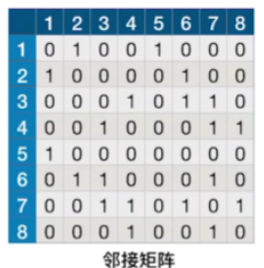
- 访问 |V| 个顶点需要O(|V|)的时间
- 查找每个顶点的邻接点都需要O(|V|)的时间,而总共有|V|个顶点
- 时间复杂度= O(|V|²)
2.邻接表存储的图
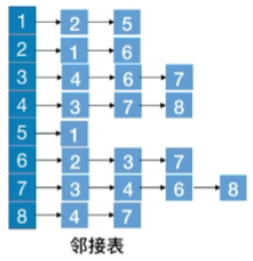
- 访问|V|个顶点需要O(|V|)的时间
- 查找各个顶点的邻接点共需要O(|E|)的时间
- 时间复杂度=O(|V|+|E|)
三.深度优先遍历序列
1.学会按照代码的思路手搓广度优先遍历序列
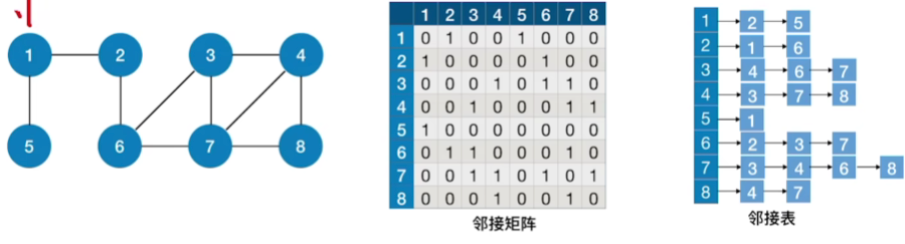
- 从2出发的深度优先遍历序列:2,1,5,6,3,4,7,8
- 从3出发的深度优先遍历序列:3,4,7,6,2,1,5,8
- 从1出发的深度优先遍历序列:1,2,6,3,4,7,8,5
2.遍历序列的可变性
-
更改上图的邻接表
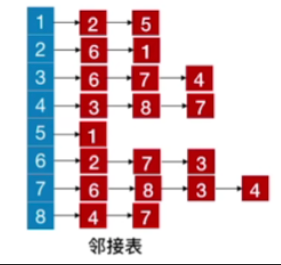
-
从2出发的深度优先遍历序列:2,6,7,8,4,3,1,5
3.结论
- 同一个图的邻接矩阵表示方式唯一,因此深度优先遍历序列唯一
- 同一个图邻接表表示方式不唯一,因此深度优先遍历序列不唯一
四.深度优先生成树
1.获得深度优先生成树的过程
-
存储图的邻接表
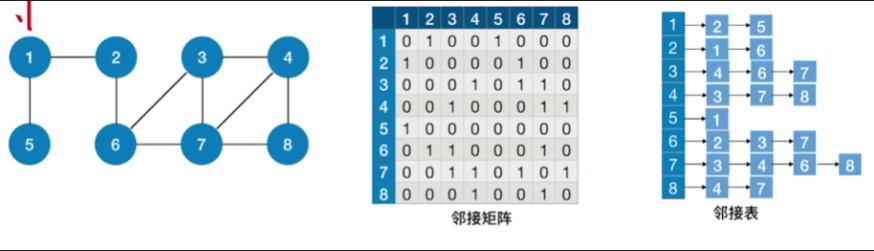
-
以2为顶点获得的广度优先遍历的路径(标红线)
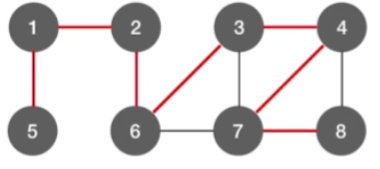
-
去掉黑线,得到广度优先生成树,并且将其化为我们熟悉的树形状
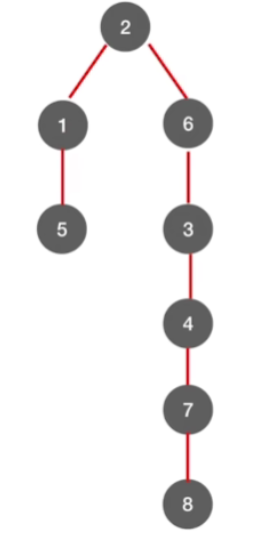
-
现在更改邻接表,按照上面的方法得到深度优先生成树
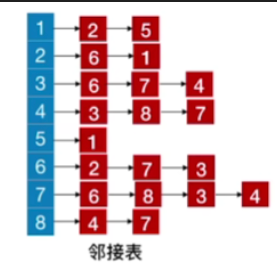
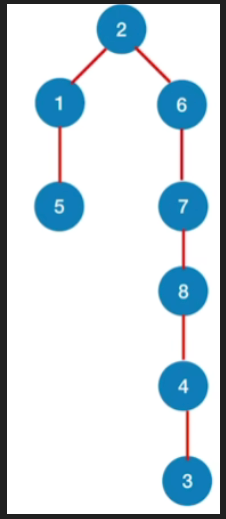
2.结论
- 广度优先生成树由广度优先遍历过程确定。由于邻接表的表示方式不唯一,因此基于邻接表的广度优先生成树也不唯一。
五.深度优先生成森林
-
非连通图
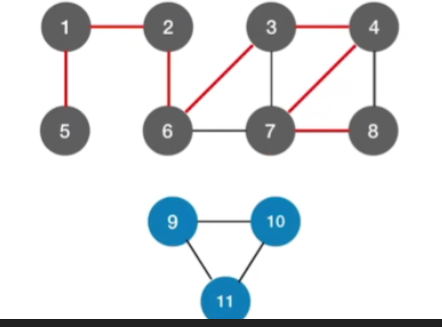
-
如果一个图它是非联通的,也就是说我们需要调用多次DFS函数,那么每调用一次DFS函数就会生成一颗这种深度优先生成树
-
那像上面的无向图总共有两个连通分量,所以需要调用两次DFS函数,因此也会对应的生成两颗深度优先生成树
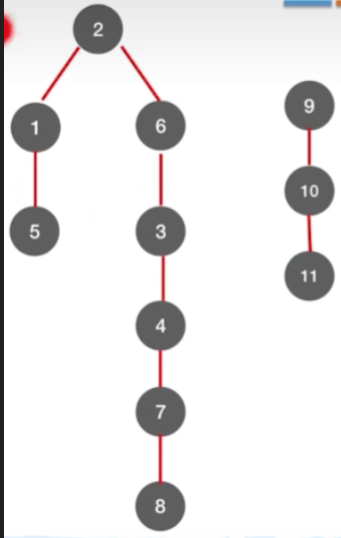
-
那这两棵树就组成了深度优先生成森林
六.图的遍历与图的连通性
1.无向图
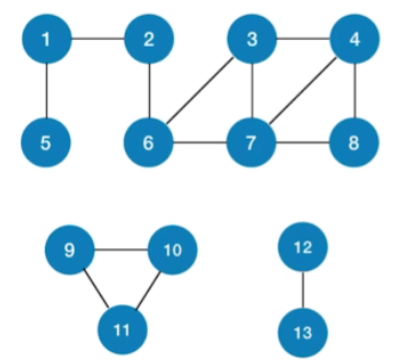
- 对无向图进行BFS/DFS遍历,调用BFS/DFS函数的次数=连通分量数
- 对于连通图,只需调用1次BFS/DFS
2.有向图
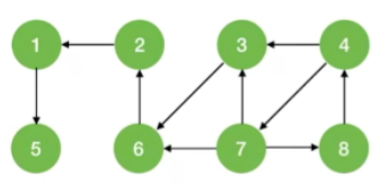
-
对有向图进行BFS/DFS遍历,调用BFS/DFS函数的次数要具体问题具体分析
-
若起始顶点到其他各顶点都有路径,则只需调用1次BFS/DFS函数
-
对于强连通图,从任一结点出发都只需调用1次 BFS/DFS
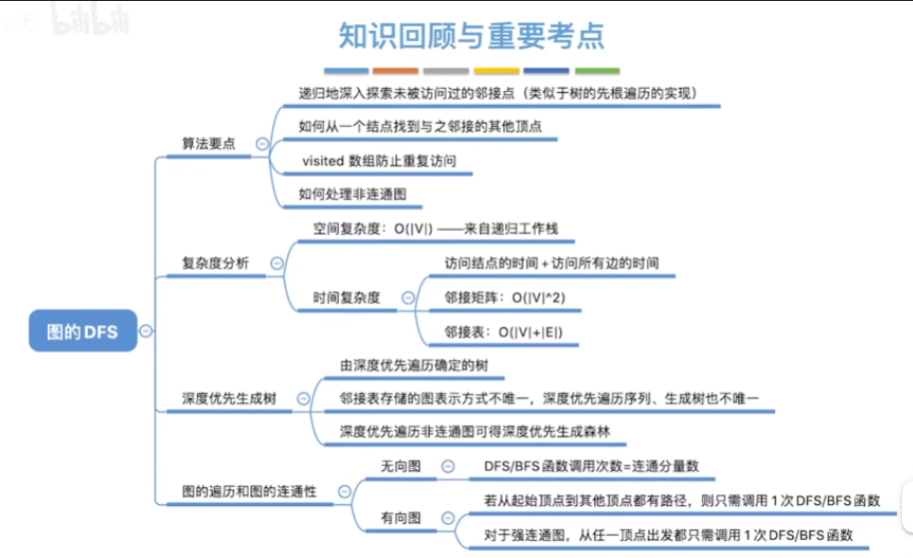
七.知识回顾与重要考点
结语
二更😁
如果想查看更多章节,请点击:一、数据结构专栏导航页
