MATLAB基于改进灰色聚类的装备技术风险评估方法

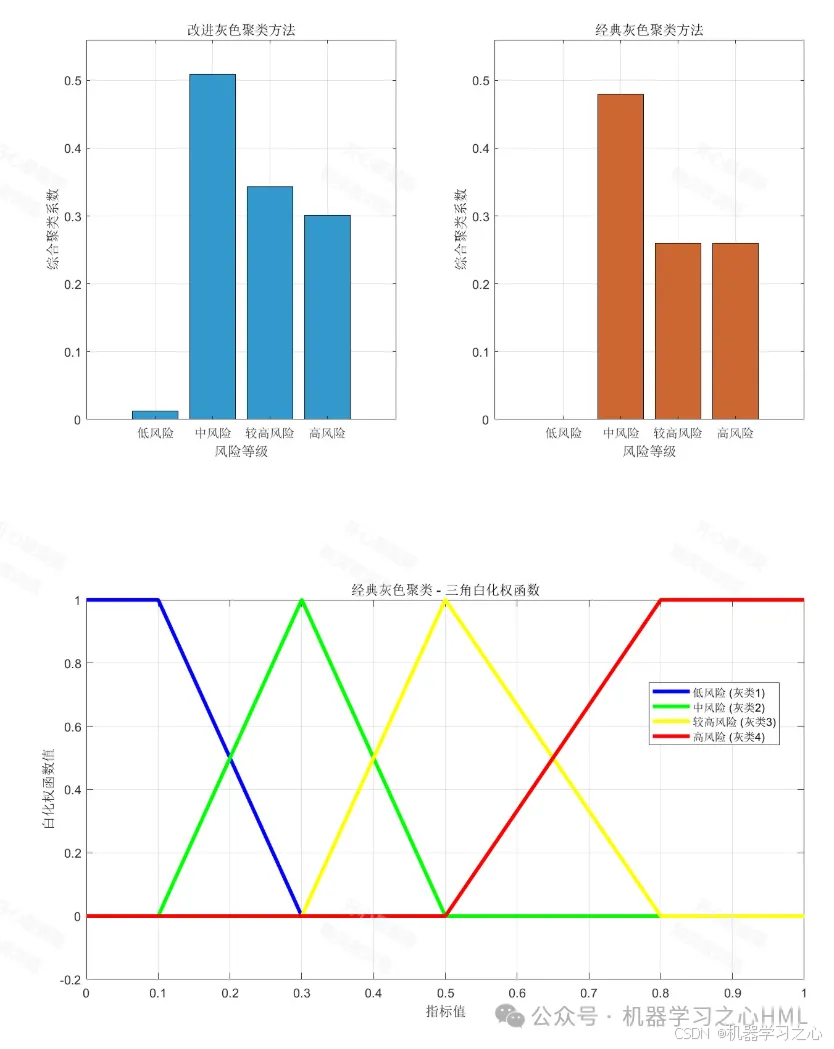
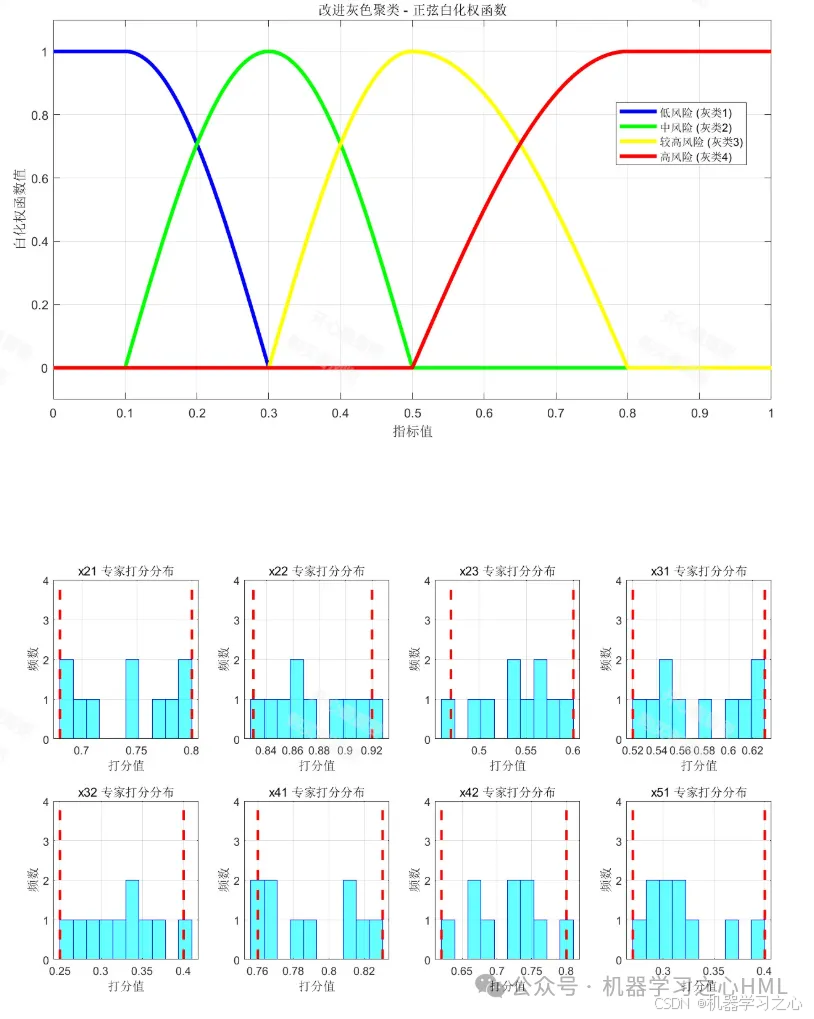
一、 方法概述与改进思路

1. 问题特性分析

装备技术风险评估通常面临：

• 信息灰色性： 新技术、新装备缺乏充足历史数据，部分风险因素难以量化
• 多维度性： 涉及技术成熟度、可靠性、保障性、兼容性等多维度指标
• 不确定性： 评估信息中存在模糊性和随机性
• 主观性： 专家判断存在主观差异

2. 传统灰色聚类的局限性

• 白化权函数形式固定，难以适应复杂风险分布
• 权重确定方法单一，不能反映指标间内在联系
• 聚类系数计算未考虑评估信息的质量差异
• 对极端风险值的敏感性不足

3. 主要改进方向

1. 白化权函数优化 - 采用更适合风险评估的混合型白化权函数
2. 权重确定方法改进 - 结合主观权重与客观权重
3. 聚类算法改进 - 引入变权或综合聚类系数
4. 结果验证机制 - 增加灵敏度分析和一致性检验

---

二、 改进灰色聚类风险评估模型构建

步骤一：建立风险评估指标体系

设装备技术风险评估有m个评估对象(装备/技术方案)，n个评估指标，s个风险等级。

• 评估对象集： O={o1,o2,...,om}O = \{o_1, o_2, ..., o_m\}O={o1​,o2​,...,om​}
• 评估指标集： I={i1,i2,...,in}I = \{i_1, i_2, ..., i_n\}I={i1​,i2​,...,in​}
• 风险等级集： R={r1,r2,...,rs}R = \{r_1, r_2, ..., r_s\}R={r1​,r2​,...,rs​} (如：低风险、较低风险、中等风险、较高风险、高风险)

指标示例：

• 技术成熟度(TRL)
• 可靠性指标(MTBF)
• 维修性指标(MTTR)
• 技术依赖性
• 技术更新周期
• 标准化程度
• 技术复杂度
• …等

步骤二：确定评估样本矩阵

收集各评估对象在各指标下的评估值，形成样本矩阵：
$$D=(d_{ij}{)}_{m\times n}$$
其中$d_{ij}$表示第$i$个对象在第$j$个指标下的评估值。

步骤三：改进一 - 优化白化权函数

传统方法改进：
采用更适合风险评估的混合型白化权函数，针对不同类型指标设计不同形式的白化权函数。

1. 成本型指标（值越小越好，如故障率）：
   $$f_j^k(d)=\{\begin{array}{ll}1& d\le {\lambda }_j^k\\ \frac{{\lambda }_j^{k+1}-d}{{\lambda }_j^{k+1}-{\lambda }_j^k}& {\lambda }_j^k<d<{\lambda }_j^{k+1}\\ 0& d\ge {\lambda }_j^{k+1}\end{array}$$

2. 效益型指标（值越大越好，如可靠性）：
   $$f_j^k(d)=\{\begin{array}{ll}0& d\le {\lambda }_j^{k-1}\\ \frac{d-{\lambda }_j^{k-1}}{{\lambda }_j^k-{\lambda }_j^{k-1}}& {\lambda }_j^{k-1}<d<{\lambda }_j^k\\ 1& d\ge {\lambda }_j^k\end{array}$$

3. 适中型指标（值在某一区间最好）：
   $$f_j^k(d)=\exp \left(-\frac{(d-{\lambda }_j^k{)}^2}{2({\delta }_j^k{)}^2}\right)$$

其中${\lambda }_j^k$为第$j$个指标第$k$个灰类的临界值，${\delta }_j^k$为适中型指标的宽度参数。

步骤四：改进二 - 组合权重确定

采用AHP-熵权法组合赋权，兼顾主观经验与客观数据。

1. 主观权重（AHP法）：

   • 构建判断矩阵
   • 计算特征向量
   • 一致性检验
   • 得主观权重向量 $W_s=(w_{s1},w_{s2},...,w_{sn})$

2. 客观权重（熵权法）：

   • 数据标准化
   • 计算熵值 $e_j=-\frac{1}{\ln m}{\sum }_{i=1}^m{p}_{ij}\ln p_{ij}$
   • 计算差异系数 $g_j=1-e_j$
   • 得客观权重 $W_o=(w_{o1},w_{o2},...,w_{on})$

3. 组合权重：
   $$w_j=\alpha w_{sj}+(1-\alpha )w_{oj}$$
   其中$\alpha$为偏好系数，通常取0.5或根据实际情况调整。

步骤五：改进三 - 综合聚类系数计算

传统聚类系数改进：

1. 考虑信息质量的加权聚类系数：
   $${\sigma }_i^k=\sum _{j=1}^n{w}_j\cdot f_j^k(d_{ij})\cdot q_{ij}$$
   其中$q_{ij}$为第$i$个对象第$j$个指标的信息质量系数，反映数据的可靠程度。

2. 引入风险偏好的修正：
   $${\sigma }_i^k=\frac{{\sum }_{j=1}^n{w}_j{f}_j^k(d_{ij})}{{\sum }_{j=1}^n{w}_j}\cdot {\beta }^k$$
   其中${\beta }^k$为第$k$个风险等级的偏好系数，可根据决策者风险态度调整。

步骤六：风险评估与等级判定

1. 构建聚类系数矩阵：
   $$\Sigma =({\sigma }_i^k{)}_{m\times s}$$

2. 风险等级判定：

   • 最大隶属度原则： 若σik∗=max⁡1≤k≤s{σik}\sigma_i^{k^*} = \max\limits_{1\leq k\leq s}\{\sigma_i^k\}σik∗​=1≤k≤smax​{σik​}，则对象$o_i$属于风险等级$r_{k^{\ast }}$
   • 置信度准则： 给定置信度$\lambda$（通常0.6-0.7），按风险等级从高到低累积，达到置信度时的等级为最终评定等级

---

三、 实例应用（简化版）

评估场景： 某新型军事装备的3项关键技术风险评估

步骤：

1. 指标体系：

   • I1: 技术成熟度(1-9级)
   • I2: 预计故障率(次/千小时)
   • I3: 技术依赖度(1-10分)

2. 风险等级： 低风险(r1)、中风险(r2)、高风险(r3)

3. 样本数据：

   技术	I1(TRL)	I2(故障率)	I3(依赖度)
   T1	6	0.8	7
   T2	4	1.5	9
   T3	7	0.5	4

4. 白化权函数参数设定（基于专家经验）：

   • I1: [8,6,4] (r1,r2,r3的临界值)
   • I2: [0.3,0.8,1.2]
   • I3: [3,6,8]

5. 权重计算：

   • AHP主观权重: [0.4, 0.35, 0.25]
   • 熵权法客观权重: [0.38, 0.42, 0.20]
   • 组合权重(α=0.5): [0.39, 0.385, 0.225]

6. 聚类系数计算与结果：

   技术	σ(r1)	σ(r2)	σ(r3)	风险等级
   T1	0.42	0.58	0.25	中风险
   T2	0.15	0.35	0.72	高风险
   T3	0.68	0.45	0.12	低风险

---

四、 方法优势与验证

1. 方法优势

• 信息利用充分： 能有效处理贫信息、不确定性评估问题
• 适应性强： 通过改进白化权函数适应不同类型风险评估指标
• 权重科学： 主客观结合避免权重确定的片面性
• 结果可靠： 改进的聚类系数提高风险评估的准确性

2. 验证方法

• 灵敏度分析： 检验权重变化对评估结果的影响
• 一致性检验： 与专家打分结果对比验证
• 案例回溯： 用历史数据验证方法的有效性
• 比较分析： 与传统灰色聚类、模糊综合评价等方法对比

3. 应用扩展

• 动态风险评估： 引入时间序列，实现风险趋势预测
• 组合评估： 与故障树分析(FTA)、贝叶斯网络等方法结合
• 可视化展示： 开发风险评估可视化系统

---

五、 结论

本方法通过白化权函数优化、组合权重确定和聚类系数改进三个方面对传统灰色聚类进行了系统改进，使其更适用于装备技术风险评估的特点。该方法能够：

1. 有效处理评估中的不确定性和信息不完整问题
2. 科学整合主观经验与客观数据
3. 提供更加准确和可靠的风险等级评定
4. 为装备技术风险管理决策提供有力支持