[优选算法专题四.前缀和——NO.31 连续数组]
题目链接:
525. 连续数组
题目描述:

题目解析:
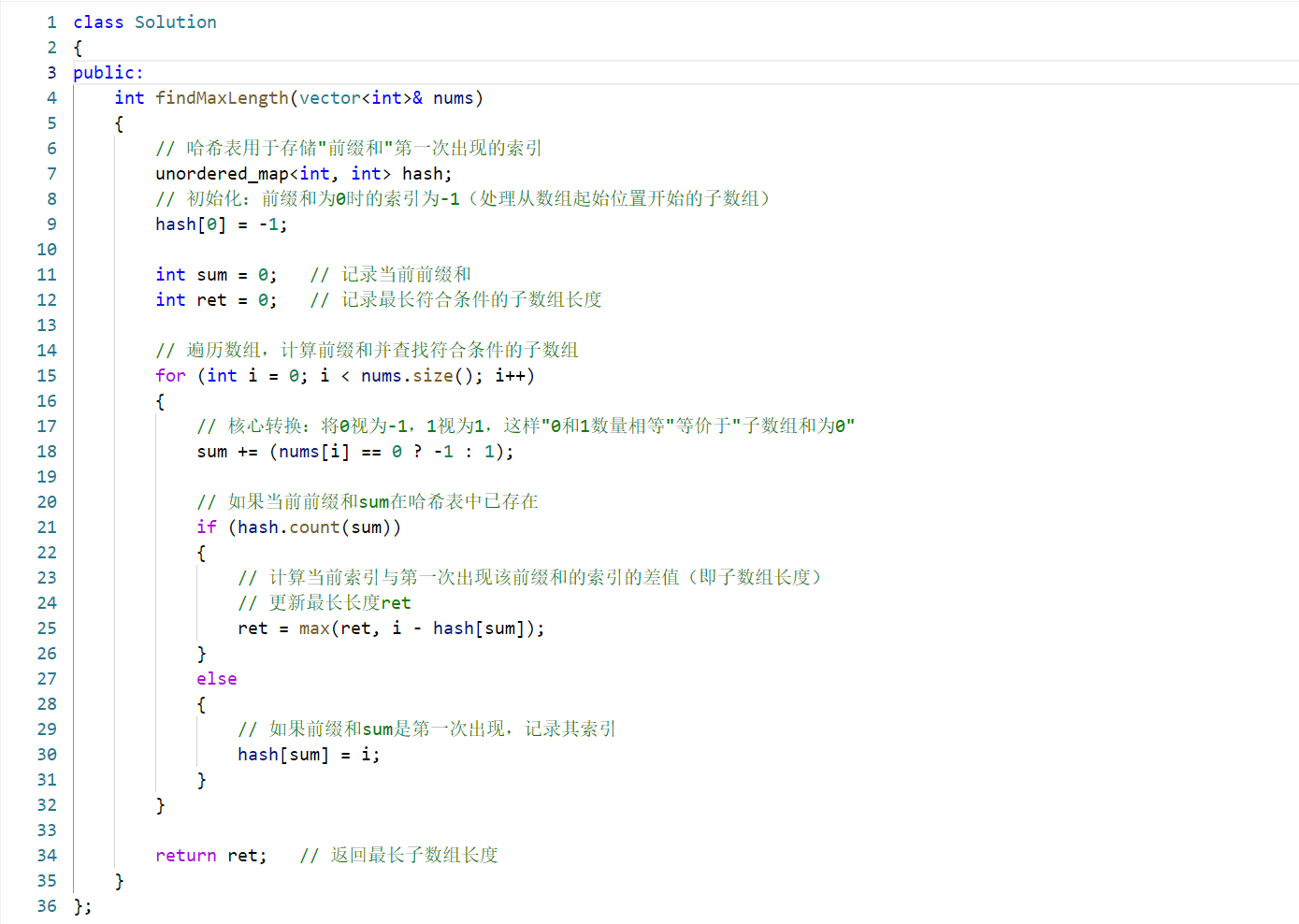
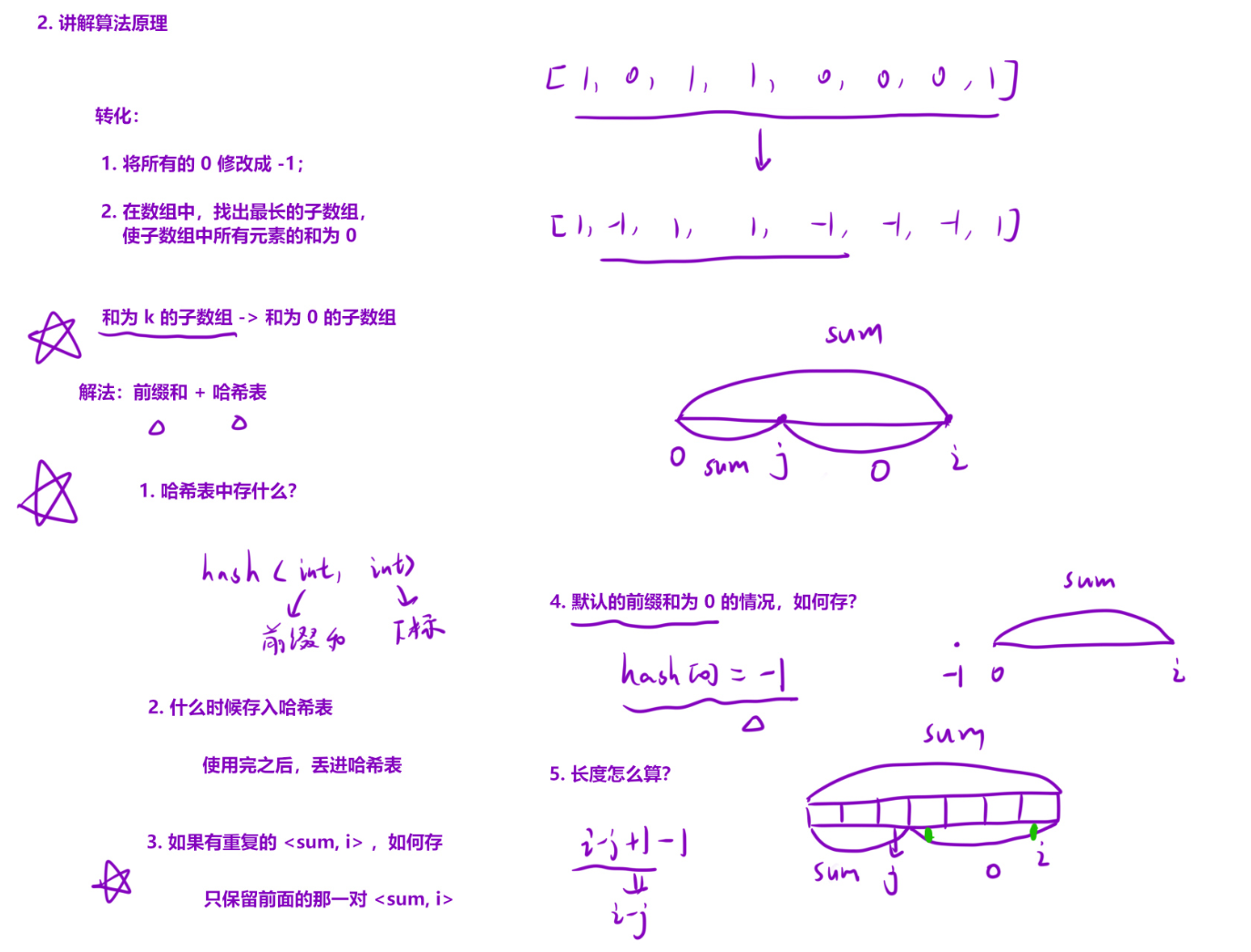
核心思路详解
-
问题转换原问题是 "找到 0 和 1 数量相等的最长连续子数组",通过将 0 转换为 - 1,1 保持为 1,问题等价于 "找到和为 0 的最长连续子数组"(因为 0 和 1 数量相等时,-1 和 1 的总和为 0)。
-
前缀和的应用设前缀和
sum[i]为数组前i个元素的和(按上述转换规则计算)。对于子数组[j+1, i],其和为sum[i] - sum[j]。若该子数组和为 0,则sum[i] = sum[j]。 -
哈希表优化哈希表记录每个前缀和第一次出现的索引。当遍历到索引
i时,若sum[i]已在哈希表中存在(设第一次出现索引为j),则子数组[j+1, i]的和为 0,其长度为i - j。通过这种方式,可在 O (1) 时间内查找历史前缀和,避免暴力枚举的 O (n²) 复杂度。 -
初始化处理哈希表初始化为
{0: -1},是为了处理从数组起始位置(索引 0)开始的子数组。例如,若sum[2] = 0,则子数组[0, 2]的长度为2 - (-1) = 3。
时间与空间复杂度
- 时间复杂度:O (n),其中 n 为数组长度,只需遍历一次数组,哈希表操作平均为 O (1)。
- 空间复杂度:O (n),最坏情况下哈希表需存储 n 个不同的前缀和。
该算法通过巧妙的问题转换和前缀和 + 哈希表的组合,高效解决了最长 0-1 相等子数组问题。
