【C++】二分查找算法习题

🎆个人主页：夜晚中的人海

今日语录：当你的才华不足以满足你的野心时，应该静下心来努力学习。

在使用二分查找算法前，我们首先要知道在什么情况下可以采用二分算法。我们普遍清楚在使用二分算法前 数据必须有序，这一回答是毋庸置疑的，但不完全正确，我们还需 判断题目中的数据是否有二段性，如果判断出有二段性，我们同样也可以采用二分算法，即使该数据不是有序的，下面就来一起看看二分查找的一些相关习题

⭐一、二分查找

题目链接：二分查找

题目描述：

解题思路：
1.这是一个最典型使用二分算法的题目，我们可以定义两个指针left和right分别指向数组的左右两区间

2.然后查找区间的中间点mid，看看中间点mid的值是否等于目标值

3.如果中间值大于目标值，说明从该区间开始一直到右区间的值都是大于目标值的，因此需要让right指针指向mid - 1的位置，让后重新执行步骤二的操作；相反如果小于目标值，说明从该区间开始一直到左区间的元素值都是小于目标值的，因此让left指向mid + 1的位置，再继续判断，直到找到目标值

代码实现：

class Solution {
public:int search(vector<int>& nums, int target) {int n = nums.size();int left = 0,right = n - 1;while(left <= right){//防溢出操作int mid = left + (right - left) / 2;if(nums[mid] < target){left = mid + 1;}else if(nums[mid] > target){right = mid - 1;}else{return mid;}}return -1;}
};

🏝️二、在排序数组中查找元素的第一个和最后一个位置

题目链接：在排序数组中查找元素的第一个和最后一个位置

题目描述：

解题思路：
1.我们可以采用二分左边界和右边界的方法

2.在二分左边界时，我们可以根据中间点mid的落点来进行更新，如果中间值mid的值小于目标值，就让left指向mid + 1的位置，否则就让right指向mid的位置（注：不能指向mid - 1，有可能mid是最终结果）

3.二分右边界时，同样也是根据mid的落点来进行判断，如果mid的值大于目标值，则让right指向mid - 1的位置，否则让left指向mid（注：同样不能指向mid + 1，mid可能是最终结果）

代码实现：

class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {int n = nums.size();//标记左端点int begin = 0;if(n == 0)return {-1,-1};//二分左端点int left = 0,right = n - 1;while(left < right){int mid = left + (right - left) / 2;if(nums[mid] < target){left = mid + 1;}else{right = mid;}}if(nums[left] != target)return {-1,-1};elsebegin = left;//二分右端点left = begin,right = n - 1;while(left < right){int mid = left + (right - left + 1) / 2;if(nums[mid] <= target)left = mid;elseright = mid - 1;}return {begin,right};}
};

🎡三、搜索插入位置

题目链接：搜索插入位置

题目描述：

解题思路：
1.给两个指针left和right分别指向左边界和右边界，mid作为中间点，根据mid指向的元素进行分析

2.如果mid指向的元素小于等于目标值，则更新left，让left指向mid（mid可能是目标值），否则让right指向mid - 1的位置，不断循环此步骤

3.循环结束后，如果left指向的元素小于目标值，说明该数组没有目标值，则返回要插入的位置（即l：left + 1）否则返回left即可

代码实现：

class Solution {
public:int searchInsert(vector<int>& nums, int target) {int n = nums.size();int left = 0,right = n - 1;while(left < right){int mid = left + (right - left + 1) / 2;if(nums[mid] <= target)left = mid;elseright = mid - 1;}if(nums[left] < target)return left + 1;elsereturn left;}
};

🚘四、x的平方根

题目链接：x的平方根

题目描述：

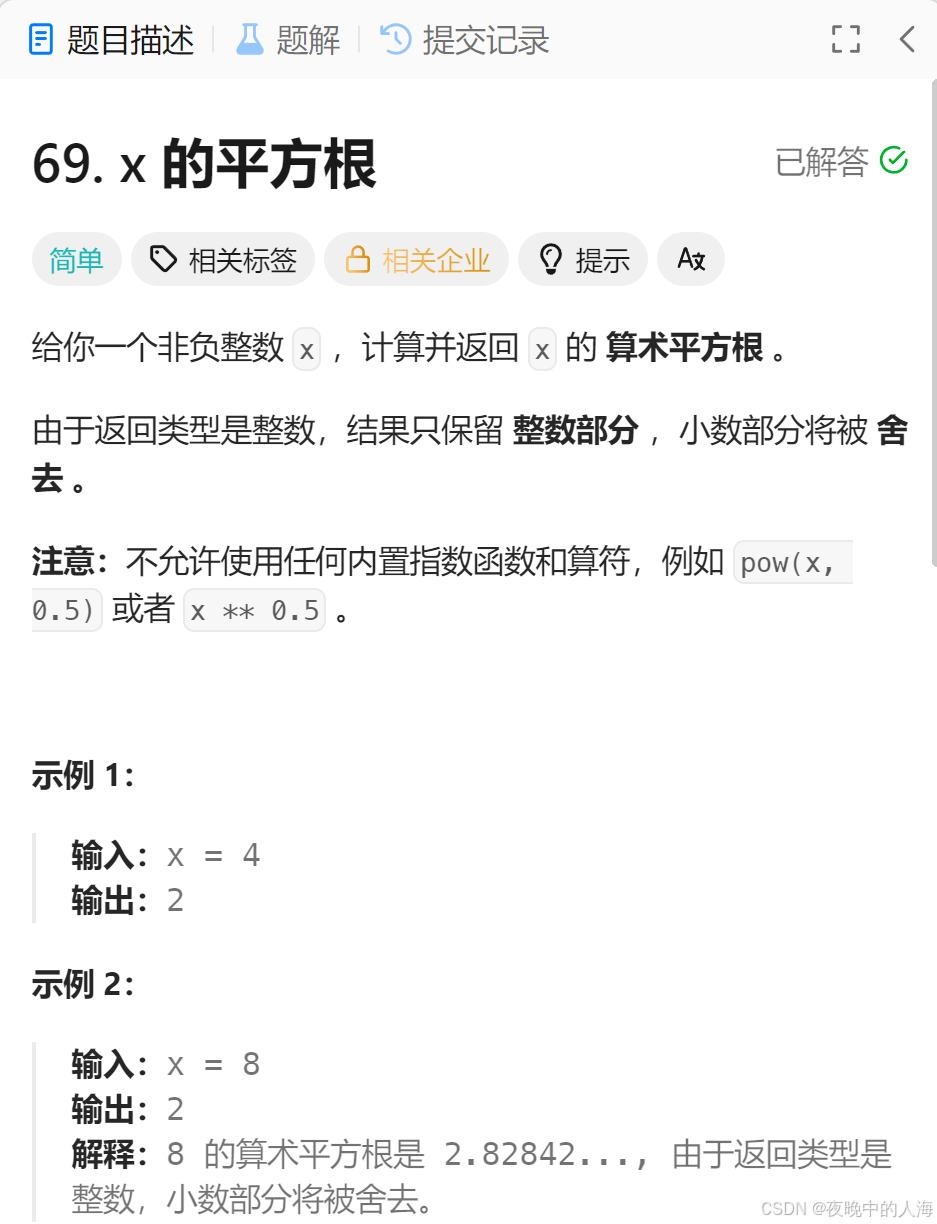
解题思路：
1.暴力枚举，依次枚举[0，x]之间的所有数i，如果i * i大于x，则返回i - 1，否则返回i

2.二分算法，定义两个指针left和right，寻找中间点mid，如果mid * mid的值小于等于x，则找到结果，让left指向mid位置，返回left即可，否则让right指向mid - 1的位置

代码实现：

class Solution {
public:int mySqrt(int x) {//处理边界情况if(x < 1)return 0;int left = 1,right = x;while(left < right){long long mid = left + (right - left + 1) / 2;if(mid * mid <= x){left = mid;}else{right = mid - 1;}}return left;}
};

🚀五、寻找峰值

题目链接：寻找峰值

题目描述：

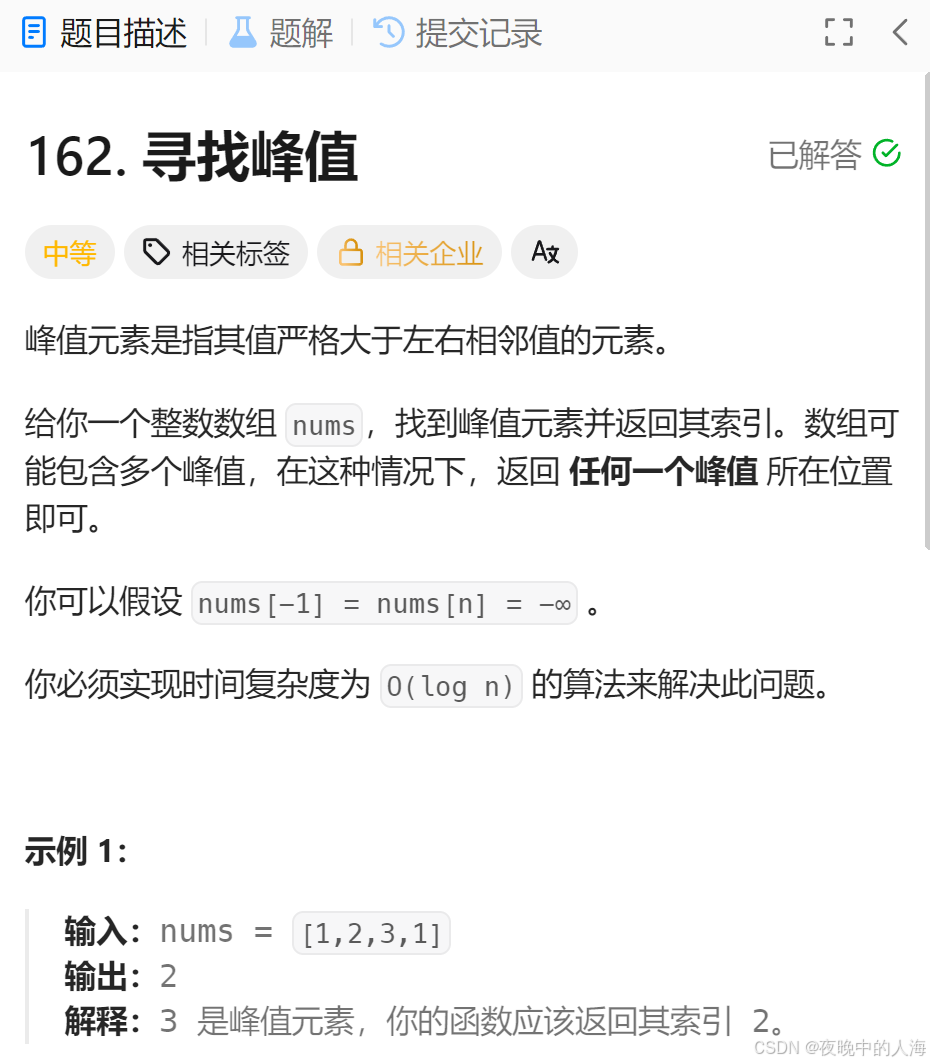
解题思路：
1.我们可以先来寻找数据是否有二段性，来看看能否使用二分算法

2.任取一个点i来进行判断，如果nums[i + 1] > nums[i]，说明右侧区域一定存在山峰（注：右侧是负无穷），我们就可以去右侧寻找结果；相反nums[i] > nums[i + 1]，说明左侧一定存在山峰，我们就可以去左侧寻找结果，判断出数据有二段性，我们就可以采用二分算法来解决

代码实现：

class Solution {
public:int findPeakElement(vector<int>& nums) {int n = nums.size();int left = 0,right = n - 1;while(left < right){int mid = left + (right - left + 1) / 2;if(nums[mid] > nums[mid - 1]){left = mid;}elseright = mid - 1;}return left;}
};

🎆六、寻找排序数组中的最小值

题目链接：寻找排序数组中的最小值

题目描述：

解题思路：

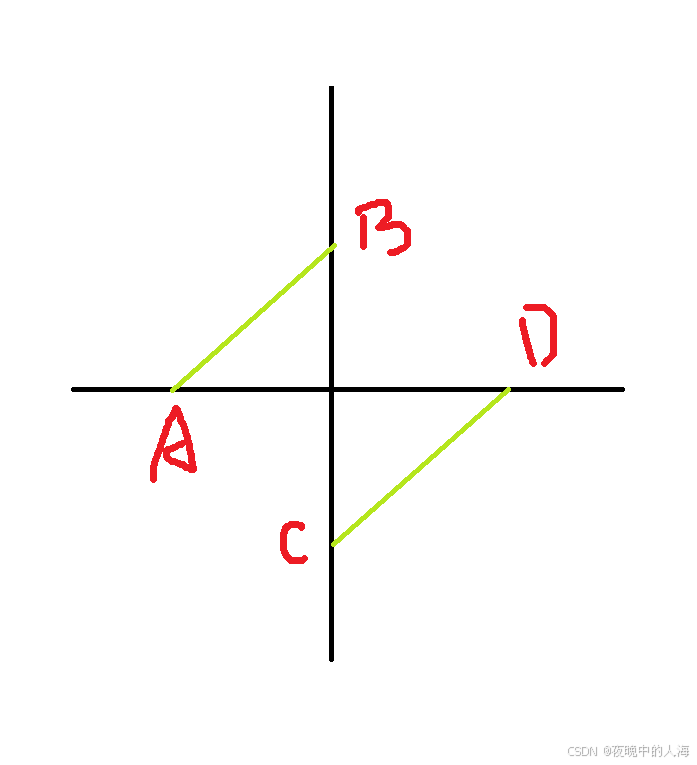
1.我们根据题目中的数组绘制如上的草图

2.根据草图我们发现[A,B]区间内的值是严格大于[C,D]区间内的值的，而且C的值是严格小于D的值的（注：C的值也可能等于D的值，当[C,D]区间内只有一个元素时），从而判断出数据有二段性，采用二分算法

3.初始化两个指针left，right，根据mid的落点来进行判断：如果mid落在[A,B]的区间内，说明mid位置的值是严格大于D点的值，则让left指向mid + 1的位置；如果mid落在[C,D]的位置上，说明mid的值是小于D点的值，因此让right指向mid

4.不断重复上述步骤，循环结束后left指向的元素就是我们要的结果，返回即可

代码实现：

class Solution {
public:int findMin(vector<int>& nums) {int n = nums.size();int left = 0,right = n - 1;int x = nums[right];while(left < right){int mid = left + (right - left) / 2;if(nums[mid] > x){left = mid + 1;}else{right = mid;}}return nums[left];}
};

🎄七、0 ~ n - 1中缺失的数字

题目链接：0 ~ n - 1中缺失的数字

题目描述：

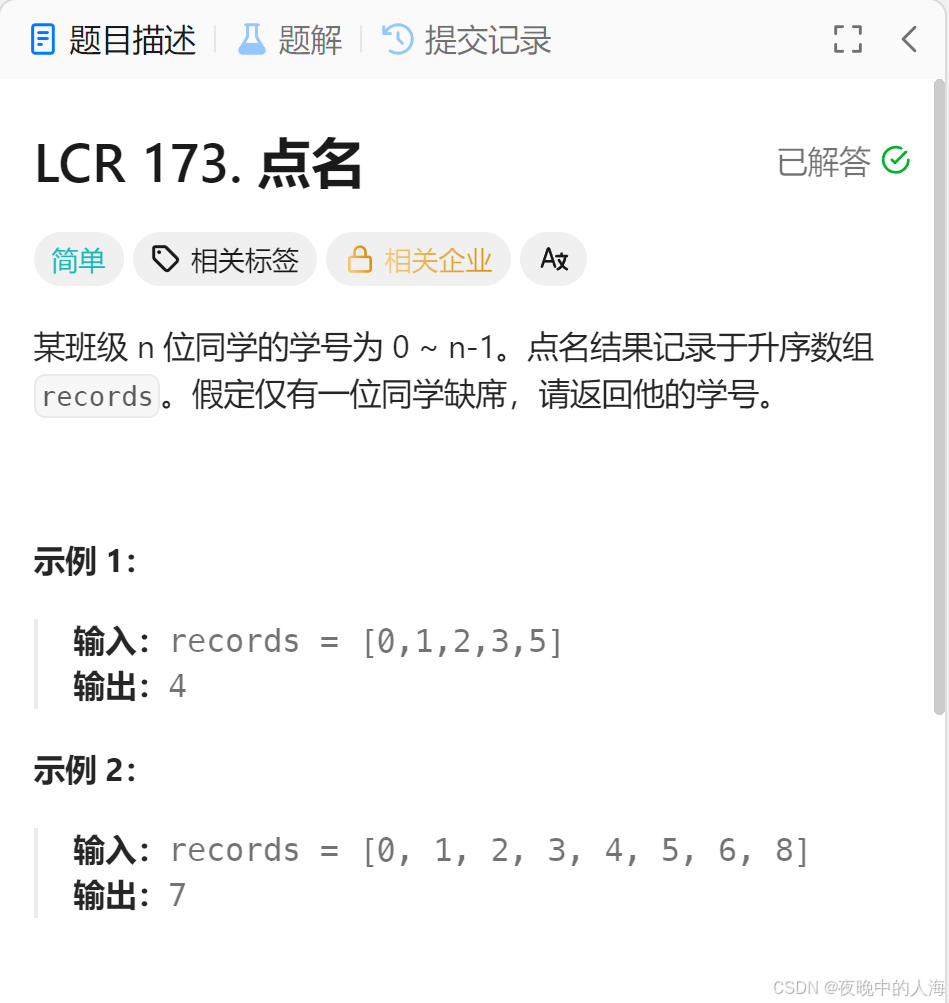
解题思路：
1.先来判断数据是否有二段性，我们发现在缺失数据位置左边，数据的元素和数组的下标都是有序的；在缺失数据位置的右边，数据的元素和数组的下标都是无序的

2.我们就可以根据这一二段性来使用二分算法

代码实现：

class Solution {
public:int takeAttendance(vector<int>& records) {int n = records.size();int left = 0,right = n;while(left < right){int mid = left + (right - left) / 2;if(records[mid] == mid){left = mid + 1;}else{right = mid;}}return left;}
};