关系数据库2.3-2.4

2.3 关系的完整性

❖实体完整性和参照完整性

◼ 关系模型必须满足的完整性约束条件称为关系的两个 不变性，应该由关系系统自动支持

❖用户定义的完整性

◼应用领域需要遵循的约束条件，体现了具体领域中的 语义约束

2.3.1 实体完整性

❖规则2.1 实体完整性规则（EntityIntegrity）

◼若属性A是基本关系R的主属性，则属性A不能取空值

◼空值就是“不知道”或“不存在”或“无意义”的值 例： 选修（学号 ，课程号，成绩） “学号、课程号”为主码 “学号”和“课程号”两个属性都不能取空值

2.3.2 参照完整性

1. 关系间的引用

❖在关系模型中实体及实体间的联系都是用关系来 描述的，自然存在着关系与关系间的引用。

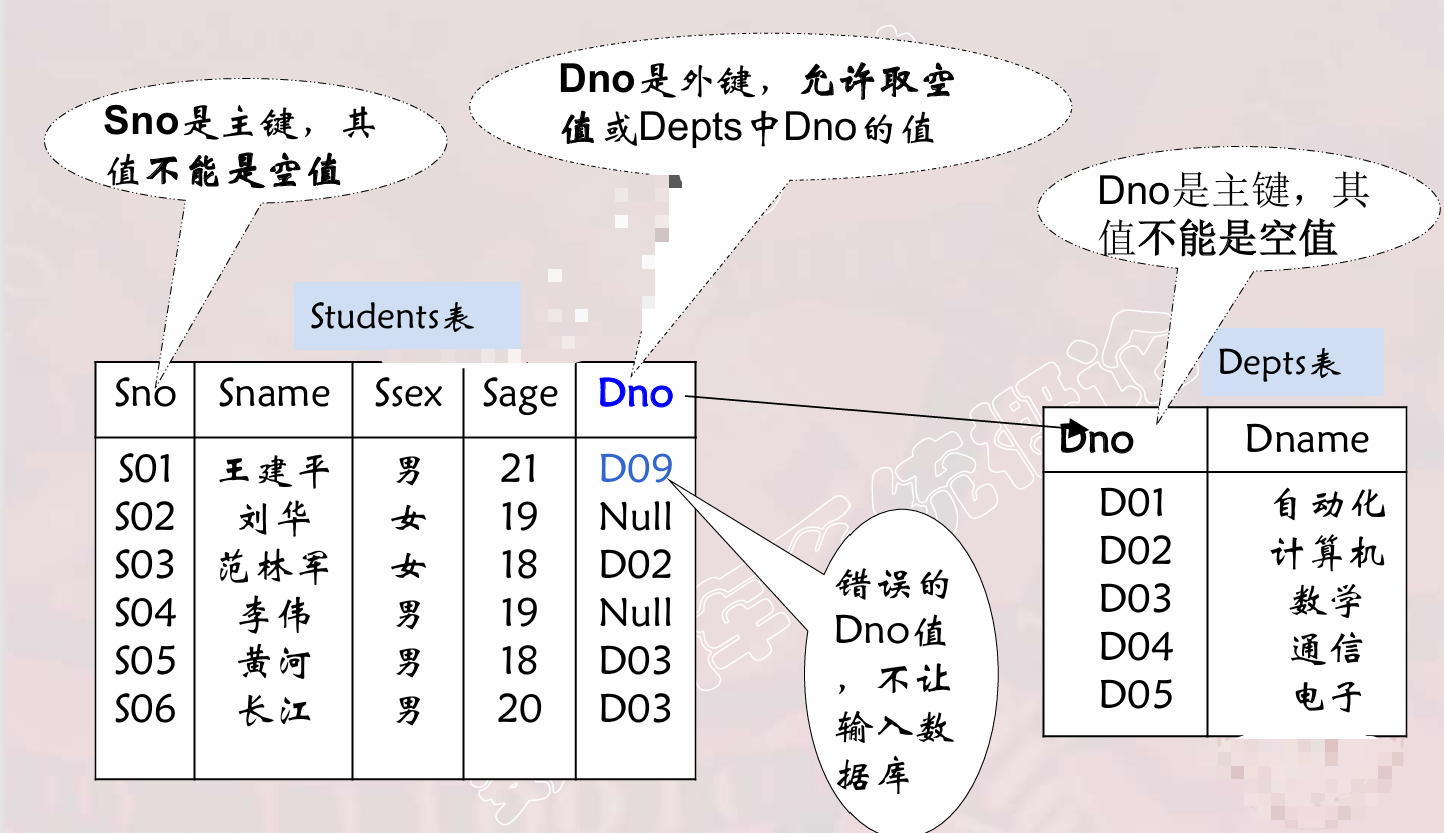
[例2.1] 学生实体、专业实体

学生（学号 ，姓名，性别，专业号，年龄） 主码

专业（专业号，专业名）主码

❖学生关系引用了专业关系的主码“专业号”。 

❖ 学生关系中的“专业号”值必须是确实存在的专业的专业号

2. 外码

❖设F是基本关系R的一个或一组属性，但不是关系R的码。 如果F与基本关系S的主码Ks相对应，则称F是R的外码

❖基本关系R称为参照关系（Referencing Relation）

❖基本关系S称为被参照关系（ReferencedRelation） 或目标关系（TargetRelation）

例[2.2] 学生、课程、学生与课程之间的多对多联系 学生（学号 ，姓名，性别，专业号，年龄） 课程（课程号 ，课程名，学分） 选修（学号 ，课程号 ，成绩）

学生实体及其内部的一对多联系 学生（学号 ，姓名，性别，专业号，年龄，班长）

❖“学号”是主码，“班长”是外码，它引用了本关系的“学号”

❖“班长” 必须是确实存在的学生的学号

❖关系R和S不一定是不同的关系

❖目标关系S的主码Ks 和参照关系的外码F必须定义 在同一个（或一组）域上

❖外码并不一定要与相应的主码同名 当外码与相应的主码属于不同关系时，往往取相同的名 字，以便于识别

3. 参照完整性规则

❖规则2.2 参照完整性规则 若属性（或属性组）F是基本关系R的外码它与基本关系S 的主码Ks相对应（基本关系R和S不一定是不同的关系）， 则对于R中每个元组在F上的值必须为：

◼ 或者取空值（F的每个属性值均为空值）

◼ 或者等于S中某个元组的主码值

[例2.1]中 学生关系中每个元组的“专业号”属性只取两类值： （1）空值，表示尚未给该学生分配专业 （2）非空值，这时该值必须是专业关系中某个元组的“专 业号”值，表示该学生不可能分配一个不存在的专业

[例2.2] 中 选修（学号 ，课程号 ，成绩） “学号”和“课程号”可能的取值 ： （1）选修关系中的主属性，不能取空值 （2）只能取相应被参照关系中已经存在的主码值

[例2.3] 中 学生（学号 ，姓名，性别，专业号，年龄，班长） “班长”属性值可以取两类值： （1）空值，表示该学生所在班级尚未选出班长 （2）非空值，该值必须是本关系中某个元组的学号值

2.3.3 用户定义的完整性

❖针对某一具体关系数据库的约束条件，反映某一 具体应用所涉及的数据必须满足的语义要求

❖关系模型应提供定义和检验这类完整性的机制， 以便用统一的系统的方法处理它们，而不需由应用程序承担这一功能

例: 课程（课程号 ，课程名，学分）

◼“课程号”属性必须取唯一值

◼非主属性“课程名”也不能取空值

◼“学分”属性只能取值{1，2，3，4}

2.4 关系代数

❖关系代数

        ◼运算对象是关系

        ◼运算结果亦为关系

        ◼关系代数的运算符有两类：集合运算符和专门的关系 运算符

❖传统的集合运算是从关系的“水平”方向即行的 角度进行

❖专门的关系运算不仅涉及行而且涉及列

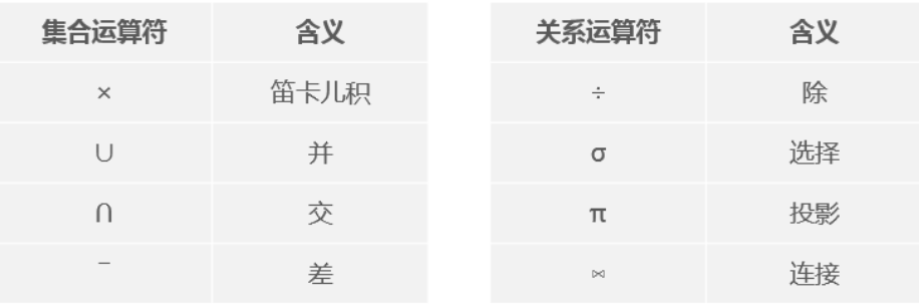
表2.4 关系代数运算符

2.4.1 传统的集合运算

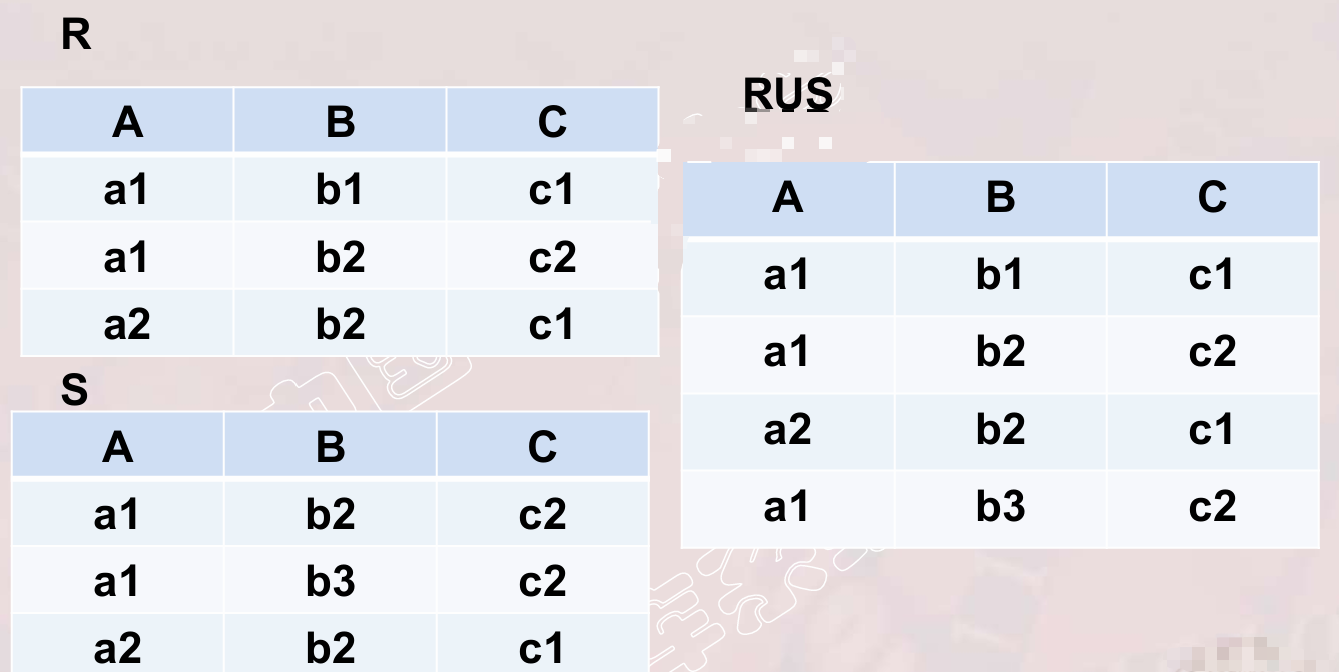
（1）并（Union）

❖R和S

◼具有相同的目n（即两个关系都有n个属性）

◼相应的属性取自同一个域

❖R∪S

◼仍为n目关系，由属于R或属于S的元组组成

（2）差（Difference）

❖R和S

◼具有相同的目n

◼相应的属性取自同一个域

❖R-S

◼仍为n目关系，由属于R而不属于S的所有元组组成 R-S ={t|tR∧tS }

（3）交（Intersection）

❖R和S

◼具有相同的目n

◼相应的属性取自同一个域

❖R∩S

◼仍为n目关系，由既属于R又属于S的元组组成 R∩S ={t|t  R∧t S} R∩S =R–(R-S）

（4）笛卡尔积（Cartesian Product）

❖严格地讲应该是广义的笛卡尔积（Extended Cartesian Product）

❖R:n目关系，k1 个元组

❖S:m目关系，k2 个元组

❖R×S ◼列：（n+m）列元组的集合 ⚫元组的前n列是关系R的一个元组 ⚫后m列是关系S的一个元组 ◼行：k1 ×k2 个元组 ⚫R×S={tr ts |tr R ∧ ts S }

2.4.2 专门的关系运算

1. 选择

❖选择又称为限制（Restriction）

❖选择运算符的含义

◼在关系R中选择满足给定条件的诸元组 σF (R) = {t|tR∧F(t)= '真'}

⚫基本形式为：X1θY1

◼F：选择条件，是一个逻辑表达式，取值为“真” 或“假”

⚫θ表示比较运算符，它可以是＞，≥，＜，≤，＝或<>

❖选择运算是从关系R中选取使逻辑表达式F为真的 元组，是从行的角度进行的运算

2. 投影

◼从R中选择出若干属性列组成新的关系 πA (R) = { t[A] | t R } A：R中的属性列

◼投影操作主要是从列的角度进行运算 π

◼投影之后不仅取消了原关系中的某些列，而且还可能 取消某些元组（避免重复行）

3. 连接

❖连接也称为θ连接

❖连接运算的含义 从两个关系的笛卡尔积中选取属性间满足一定条件的元组 tr ts R S={ |tr R∧ts S∧tr [A]θts [B]} AθB

⚫θ：比较运算符

⚫A和B：分别为R和S上度数相等且可比的属性组

◼连接运算从R和S的广义笛卡尔积R×S中选取R关系在 A属性组上的值与S关系在B属性组上的值满足比较关 系θ的元组

❖两类常用连接运算

◼等值连接（equijoin）

⚫θ为“＝”的连接运算称为等值连接

⚫从关系R与S的广义笛卡尔积中选取A、B属性值相等 的那些元组，即等值连接为： A=B tr ts R S = { | tr R∧ts S∧tr [A] = ts [B] }

◼自然连接（Natural join）

⚫自然连接是一种特殊的等值连接 ➢两个关系中进行比较的分量必须是相同的属性组 ➢在结果中把重复的属性列去掉

⚫自然连接的含义 R和S具有相同的属性组B R S= { [U-B] | tr R∧ts S∧tr [B] = ts [B] }

❖一般的连接操作是从行的角度进行运算。 自然连接还需要取消重复列，所以是同时从行和列的角度 进行运算。

❖悬浮元组（Dangling tuple）

◼两个关系R和S在做自然连接时，关系R中某些元组 有可能在S中不存在公共属性上值相等的元组，从而 造成R中这些元组在操作时被舍弃了，这些被舍弃的 元组称为悬浮元组。

❖外连接（Outer Join）

◼如果把悬浮元组也保存在结果关系中，而在其他属性 上填空值(Null)，就叫做外连接

◼左外连接(LEFT OUTER JOIN或LEFT JOIN) ⚫只保留左边关系R中的悬浮元组

◼右外连接(RIGHT OUTER JOIN或RIGHT JOIN) ⚫只保留右边关系S中的悬浮元组

4. 除运算

给定关系R(X，Y)和S(Y，Z)，其中X，Y，Z为属性组。 R中的Y与S中的Y可以有不同的属性名，但必须出自相同的 域集。

R与S的除运算得到一个新的关系P(X)，

P是R中满足下列条件的元组在 X属性列上的投影： 元组在X上分量值x的象集Yx 包含S在Y上投影的集合，记作： R÷S={tr [X]|tr R∧πY (S)Yx } Yx ：x在R中的象集，x=tr [X]

❖在关系R中，A可以取四个值{a1，a2，a3，a4} a1 的象集为 {(b1 ，c2 )，(b2 ，c3 )，(b2 ，c1 )} a2 的象集为 {(b3 ，c7 )，(b2 ，c3 )} a3 的象集为 {(b4 ，c6 )} a4 的象集为 {(b6 ，c6 )}

❖S在(B，C)上的投影为 {(b1，c2)，(b2，c1)，(b2，c3) }

❖只有a1 的象集包含了S在(B，C)属性组上的投影 所以 R÷S={a1 }

❖关系代数运算

◼ 关系代数运算 ⚫并、差、交、笛卡尔积、投影、选择、连接、除

◼ 基本运算 ⚫并、差、笛卡尔积、投影、选择

◼ 交、连接、除 ⚫可以用5种基本运算来表达 ⚫ 引进它们并不增加语言的能力，但可以简化表达