初识C语言11.数据在内存中的存储
目录
前言:
一、整数在内存中的存储:补码的“设计智慧”
1.1 补码的本质:简化运算
二、大小端字节序:多字节数据的“排列游戏”
2.1 字节序的定义
2. 2为什么要关心字节序?
2.3练习
三、浮点数在内存中的存储:IEEE 754的“精密编码”
3.1 IEEE 754标准:三部分拆分
3. 2代码验证浮点数存储
四、总结:理解内存存储的意义
完
前言:
在C语言编程中,数据在内存的存储是“看不见但关键”的底层逻辑。它决定了变量如何被读取、运算,甚至影响程序的正确性与跨平台性。下面从整数、字节序、浮点数三个核心维度,结合原理、示例与代码,深度解析。
一、整数在内存中的存储:补码的“设计智慧”
在计算机中,数据是以二进制的形式存储在内存中的。对于整数的存储,主要有原码、反码和补码三种方式。每种方式都由符号位和数值位组成。符号位占一个bit,用0表示正数,1表示负数,其余的位为数值位。
数据存放内存中其实存放的是二进制的补码:
为什么要用补码呢?
1.1 补码的本质:简化运算
为使用补码可以将符号位和数值域统一处理,同时加法和减法也可以统一处理。
核心逻辑是:
- 正数:补码 = 原码(直接存储二进制值)。
- 负数:补码 = 原码(符号位不变)取反 + 1。
示例:
int a = 5 与 int b = -5 的存储
- a = 5 (二进制原码: 00000000 00000000 00000000 00000101 ):
补码与原码一致,直接存入内存,即 0x00000005 。
- b = -5 (原码: 10000000 00000000 00000000 00000101 ):
① 原码取反(符号位不变): 11111111 11111111 11111111 11111010 。
② 取反后 + 1: 11111111 11111111 11111111 11111011 (补码),存入内存为 0xFFFFFFFB 。二、大小端字节序:多字节数据的“排列游戏”
2.1 字节序的定义
多字节数据(如 int 占4字节)在内存中,字节的顺序分为两种:
- 大端序(Big-Endian):高位字节存低地址,低位字节存高地址。
例: 0x12345678 → 内存顺序(低地址到高地址): 12 34 56 78 。
- 小端序(Little-Endian):低位字节存低地址,高位字节存高地址。
例: 0x12345678 → 内存顺序(低地址到高地址): 78 56 34 12 。
2. 2为什么要关心字节序?
跨平台通信(如网络传输、文件读写)时,不同设备字节序可能不同。若不统一,会出现“数据错乱”。
2.3练习
请简述大端字节序和小端字节序的概念,设计一个小程序来判断当前机器的字节序
#include <stdio.h>
int check_sys()
{
int i = 1;
return (*(char *)&i);
}
int main()
{
int ret = check_sys();
if(ret == 1)
{
printf("⼩端\n");
}
else
{
printf("⼤端\n");
}
return 0;
}三、浮点数在内存中的存储:IEEE 754的“精密编码”
3.1 IEEE 754标准:三部分拆分
浮点数( float / double )遵循IEEE 754标准,将数值拆为:
- 符号位(S):1位,0表示正,1表示负。
- 指数位(E): float 占8位(偏移量127), double 占11位(偏移量1023)。
- 尾数位(M): float 占23位, double 占52位(隐含最高位“1”,节省1位存储)。

示例: float c = 5.5 的存储过程
步骤1:将 5.5 转为二进制科学计数法。5.5 → 二进制: 101.1 → 科学计数法: 1.011 × 2² 。步骤2:拆分三部分。- 符号位(S):0(正数)。
- 指数位(E):指数 2 + 偏移量 127 = 129 → 二进制: 10000001 。
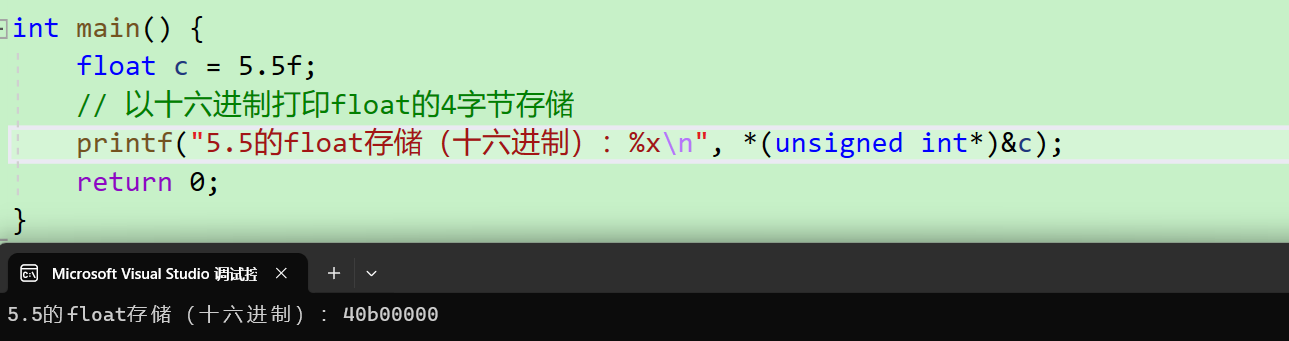
- 尾数位(M): 011 (去掉隐含的“1”),剩余20位补0 → 01100000000000000000000 。步骤3:组合为32位二进制。0 10000001 01100000000000000000000 → 十六进制: 0x40B00000 。3. 2代码验证浮点数存储
#include <stdio.h>
int main() {float c = 5.5f;// 以十六进制打印float的4字节存储printf("5.5的float存储(十六进制):%x\n", *(unsigned int*)&c); return 0;
}输出:
四、总结:理解内存存储的意义
掌握数据在内存的存储,能帮我们:
- 避免整数溢出(如 int 最大值加1变成负数)。
- 解释浮点数精度丢失(如 0.1 + 0.2 != 0.3 ,因二进制无法精确表示部分小数)。
- 解决跨平台数据兼容问题(如网络传输前统一字节序)。
这些底层知识,是C语言开发者从“写能运行的代码”到“写健壮、高效代码”的必经之路。
