the scientist and engineer‘s guide to DSP：5 Linear Systems

信号与系统

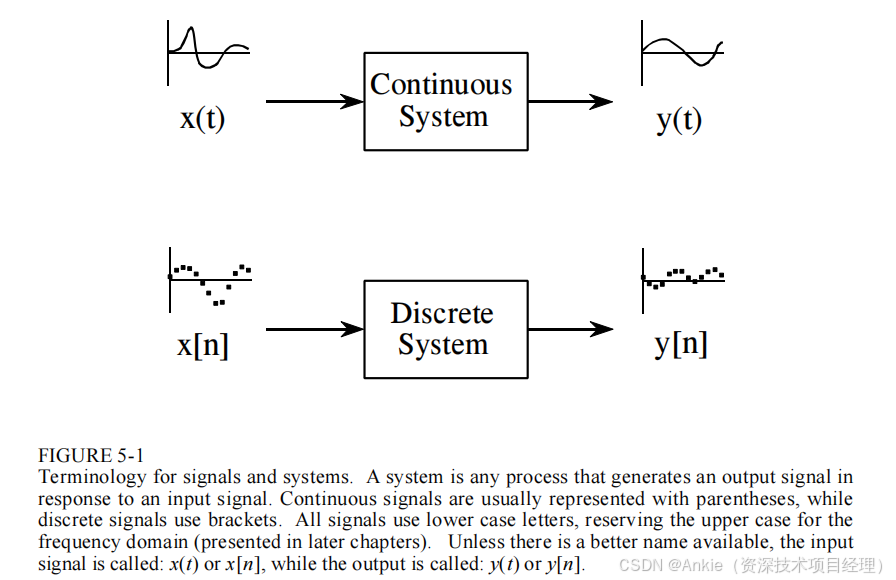
信号是对一个参数随另一个参数变化情况的描述。例如，电子电路中电压随时间的变化，或者图像中亮度随距离的变化。系统则是指任何能够对输入信号做出响应并产生输出信号的过程。图5-1中的方框图对此进行了说明。连续系统的输入和输出为连续信号，例如模拟电子系统中的信号。离散系统的输入和输出为离散信号，例如操纵数组中存储值的计算机程序所处理的信号。
信号命名遵循若干规则。这些规则在数字信号处理（DSP）领域并不总是被严格遵守，但它们非常常见，你应该牢记。若没有清晰的符号表示，数学本身就已足够复杂难懂。首先，连续信号使用圆括号，例如：x(t)和y(t)，而离散信号使用方括号，例如：x[n]和y[n]。其次，信号使用小写字母表示。大写字母则保留用于频域表示，这将在后续章节中讨论。第三，信号的命名通常能直观反映其所代表的参数。例如，随时间变化的电压可命名为：v(t)，或者每日测量的股票市场价格可命名为：p[d]。

在讨论信号与系统时，人们常常并不明确知晓所代表的具体参数。这就像在代数中使用x和y，却不给这些变量赋予实际物理意义一样。由此引出信号命名的第四条规则。若没有更具描述性的名称可用，离散系统的输入信号通常被称为：x[n]，输出信号则被称为：y[n]。对于连续系统，则使用信号x(t)和y(t)来表示。

线性性的要求

如果一个系统具备两个数学特性：齐次性（homogeneity，发音：[həˌmɑːdʒɪˈnɪti]）和可加性，则称该系统为线性系统。若能证明一个系统同时具备这两个特性，那么就证明了这个系统是线性的。同样地，若能证明一个系统不具备其中一个或两个特性，那就证明了这个系统不是线性的。第三个特性——时移不变性（shift invariance），并非线性性的严格要求，但对于大多数数字信号处理（DSP）技术而言，它却是必不可少的特性。当你在数字信号处理领域看到“线性系统”这一术语时，除非有理由认为并非如此，否则应假定它包含时移不变性。这三个特性构成了线性系统理论定义和应用的数学基础。在本章稍后部分，我们将探讨更直观地理解线性性的方法。现在，让我们先来了解一下这些正式的数学特性。

齐次性

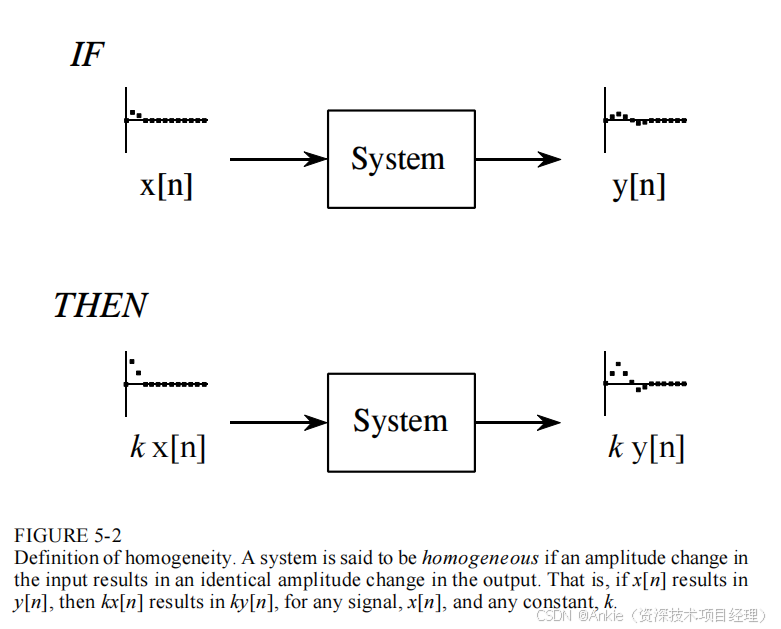
如图5-2所示，齐次性意味着输入信号幅度的变化会导致输出信号幅度相应地变化。用数学语言来说，如果输入信号x[n]产生的输出信号为y[n]，那么对于任意输入信号和常数k，输入k x[n]将产生输出k y[n]。

一个简单的电阻为齐次系统和非齐次系统均提供了很好的示例。若系统的输入是电阻两端的电压v(t)，系统的输出是流经电阻的电流i(t)，则该系统是齐次的。欧姆定律可为此提供保证：若电压升高或降低，电流也会相应地升高或降低。现在，考虑另一个系统，其中输入信号是电阻两端的电压v(t)，但输出信号是电阻上消耗的功率p(t)。由于功率与电压的平方成正比，因此，若输入信号增大为原来的两倍，输出信号则会增大为原来的四倍。该系统不具有齐次性，因此不可能是线性的。

可加性

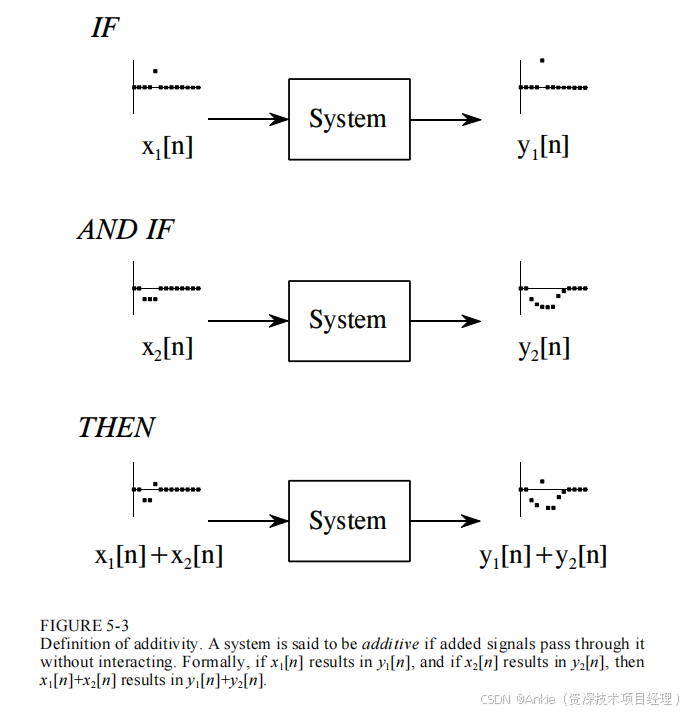
可加性这一特性如图5-3所示。考虑一个系统，输入x1[n]产生输出y1[n]。进一步假设，不同的输入x2[n]产生另一个输出y2[n]。若对于所有可能的输入信号，输入x1[n] + x2[n]会产生输出y1[n] + y2[n]，则称该系统具有可加性。换句话说，输入端相加的信号会在输出端产生相加的信号。

关键在于，相加的信号在通过系统时不会相互干扰。举个例子，设想你和埃德娜姨妈（Aunt Edna）与伯尼姨夫（Uncle Bernie）打电话的场景。埃德娜姨妈开始长篇大论地讲述她今年种的小萝卜长势有多好。与此同时，背景中伯尼姨夫正冲着狗大喊大叫，因为狗在他最喜欢的椅子上“闯祸”了。这两个声音信号叠加在一起，通过电话网络以电子方式传输。由于该系统具有可加性，你听到的声音是这两个声音叠加后的效果，就如同它们单独传输时声音的总和。你听到的是埃德娜和伯尼的声音，而不是一个叫“埃德娜伯尼”的怪物的声音。

非可加性电路的一个典型例子是无线电发射机中的混频级。此时存在两个信号：一个是包含语音或音乐的音频信号，另一个是施加到天线上便能在空间中传播的载波。这两个信号相加后，施加到一个非线性元件上，比如一个PN结二极管。这会导致两个信号合并，形成第三个信号——一种调制无线电波，它能够将信息远距离传输。

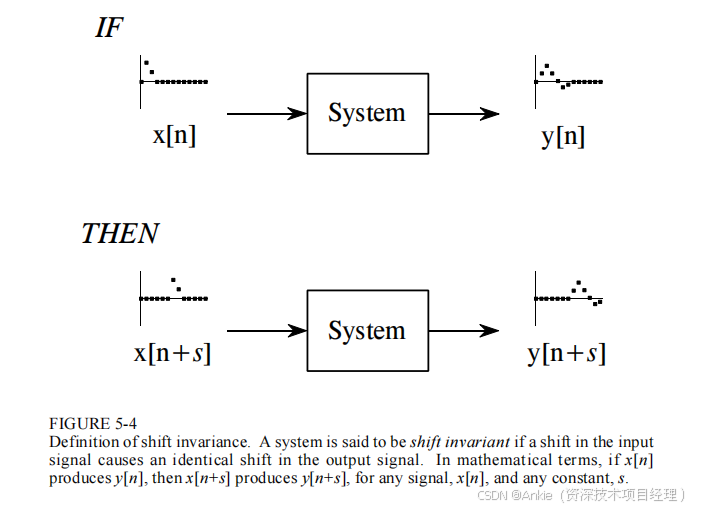
如图5-4所示，时移不变性意味着输入信号的时移只会导致输出信号产生完全相同的时移。用更正式的表述来说，如果输入信号x[n]产生输出y[n]，那么对于任何输入信号和任意常数s，输入信号x[n + s]将产生输出y[n + s]。要特别注意这种时移的数学表示方法，后续章节将会用到。通过对自变量n加上一个常数s，波形可以在水平方向上向前或向后移动。例如，当s = 2时，信号向左移动两个采样点；当s = -2时，信号向右移动两个采样点。

时移不变性之所以重要，是因为它意味着系统的特性不会随时间（或任何自变量）的改变而改变。如果输入信号中出现一个脉冲导致输出信号产生一个特定响应，那么可以确信，另一个同样的脉冲也会产生完全相同的响应。你遇到的大多数系统都具有时移不变性。这是件幸运的事，因为要处理运行过程中特性会发生变化的系统是很困难的。例如，假设你设计了一个数字滤波器，用于补偿电话传输线路的劣化影响。你的滤波器让声音听起来更自然、更易理解。然而，出乎你意料的是，冬天来了，你发现电话线路的特性随温度发生了变化。此时，你的补偿滤波器不再匹配，效果也大不如前。这种情况可能需要一种更复杂的算法，能够适应不断变化的条件。

为什么齐次性和可加性在线性性中起着关键作用，而时移不变性却相对次要呢？这是因为线性性是一个非常宽泛的概念，涵盖的远不止信号和系统。例如，考虑一位农民以每箱2美元的价格出售橙子，以每箱5美元的价格出售苹果。如果这位农民只卖橙子，那么10箱他能卖20美元，20箱能卖40美元，这种交易具有齐次性。如果他卖出20箱橙子和10箱苹果，那么他将得到：20×2美元 + 10×5美元 = 90美元。这与两种水果分开卖得到的金额是一样的，因此这种交易具有可加性。这种商品销售既具有齐次性又具有可加性，因此是一个线性过程。然而，由于其中不涉及信号，所以这并非一个系统，时移不变性也就没有意义了。可以认为，时移不变性是当涉及信号和系统时，线性性所需具备的一个额外方面。

静态线性与正弦保真性

齐次性、可加性和时移不变性之所以重要，是因为它们为定义线性系统提供了数学基础。然而，仅凭这些特性，大多数科学家和工程师仍难以直观理解线性系统的本质。此时，静态线性和正弦保真性这两大特性往往能提供帮助。从数学角度看，这两大特性并非尤为重要，但它们与人类对线性系统的思考和理解方式息息相关。因此，你应特别关注本节内容。

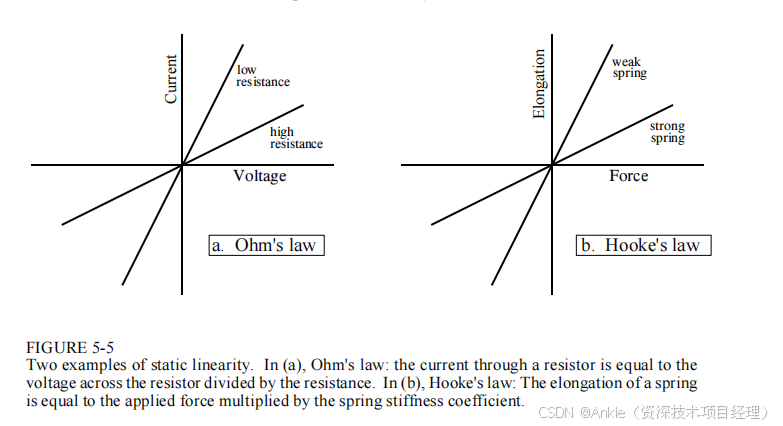
静态线性描述了线性系统在信号不发生变化（即信号为直流电或静态信号）时的响应特性。线性系统的静态响应非常简单：输出等于输入乘以一个常数。也就是说，将可能的输入值与对应的输出值绘制成图，会得到一条经过原点的直线。图5-5展示了两个常见线性系统的静态响应：电阻的欧姆定律和弹簧的胡克定律。作为对比，图5-6展示了两个非线性系统的静态关系：PN结二极管以及铁的磁性特性。

所有线性系统都具备静态线性这一特性。反之通常成立，但并非绝对。有些系统表现出静态线性，但对于变化的信号而言却不具备线性。不过，有一类非常常见的系统，仅通过静态线性就能完全理解其特性。对于这类系统，无论输入信号是静态的还是变化的，都不影响其特性。这类系统被称为无记忆系统，因为其输出仅取决于输入的当前状态，而与输入的历史无关。例如，电阻中的瞬时电流仅取决于其两端的瞬时电压，而与信号如何达到当前值无关。如果一个系统具有静态线性且是无记忆的，那么该系统必定是线性的。这为我们理解（并证明）这类简单系统的线性性提供了一种重要方法。

线性系统的一个重要特性在于其对正弦波的处理方式，我们将这一特性称为正弦保真性：若线性系统的输入为正弦波，则输出也必为正弦波，且频率与输入完全相同。正弦波是唯一具备这一特性的波形。例如，我们没有理由期望输入线性系统的方波能在输出端仍保持方波形态。尽管输入正弦波能确保输出正弦波，但二者的幅度和相位可能有所不同。这一点从你所掌握的电子学知识中应该有所了解：电路的特性可通过其频率响应来描述，即电路增益和相位随频率变化的曲线图。

现在，我们反过来思考一个问题：如果一个系统对正弦波输入总是产生正弦波输出，那么该系统是否一定是线性的？答案是否定的，但这类例外情况很少见，且通常显而易见。例如，设想一个系统内部藏着一个“恶作剧精灵”，它的目的就是误导你。这个精灵有一台示波器来观察输入信号，还有一台正弦波发生器来产生输出信号。当你向系统输入一个正弦波时，精灵会迅速测量其频率，并调整信号发生器以产生相应的输出。当然，这个系统并非线性系统，因为它不具备可加性。为了证明这一点，我们将两个正弦波相加后输入系统。此时，精灵只能产生一个单一的正弦波作为输出。这个例子并非如你想象的那样牵强；锁相环的工作方式就与此类似。

为了更好地理解线性性，我们可以想象一位技术人员正在判断一个电子设备是否为线性系统。这位技术人员会将一个正弦波发生器连接到设备的输入端，并将一台示波器连接到输出端。输入正弦波后，技术人员会观察输出是否也为正弦波。例如，输出信号顶部或底部不能被削平，上半部分不能与下半部分不同，信号过零点时不能出现失真等。接下来，技术人员会改变输入信号的幅度，并观察输出信号的变化。如果系统是线性的，输出信号的幅度必须与输入信号的幅度成比例变化。最后，技术人员会改变输入信号的频率，并验证输出信号的频率是否相应变化。在改变频率的过程中，输出信号的幅度和相位可能会发生变化，但在线性系统中这是完全允许的。在某些频率下，输出信号甚至可能为零，即幅度为零的正弦波。如果技术人员观察到上述所有现象，他就会得出结论：该系统是线性的。虽然这一结论并非严格的数学证明，但其可信度是相当高的。

线性与非线性系统示例

表 5-1 提供了一些常见的线性系统与非线性系统的示例。在浏览这些列表时，请同时牢记数学家对线性性的定义（齐次性、可加性和时移不变性），以及大多数科学家和工程师所采用的非正式理解方式（静态线性与正弦保真性）。

线性系统示例

• 声波与电磁波等波的传播
• 由电阻、电容和电感构成的电路
• 电子电路，如放大器和滤波器
• 由质量块、弹簧和阻尼器（减震器）相互作用产生的机械运动
• 由微分方程描述的系统，如电阻-电容-电感网络
• 信号与常数相乘，即信号的放大或衰减
• 信号变化，如回声、共振和图像模糊
• 输出始终等于输入的单位系统
• 输出始终为零的零系统，无论输入如何
• 微分与积分，以及离散信号的一阶差分和累加等类似运算
• 非线性系统中的微小扰动，例如，经适当偏置的晶体管对小信号的放大
• 卷积运算，即输出中的每个值均表示为输入中各值与一组加权系数乘积之和的数学运算
• 递归运算，一种与卷积类似的运算，但除了使用输入值外，还会使用先前计算出的输出值

非线性系统示例

• 不具备静态线性的系统，例如电阻两端的电压与功率关系：P=RV2​；热物体辐射的能量发射与其温度的关系：R=kT4；透过一定厚度半透明材料的光强：I=e−αT，等等
• 不具备正弦保真性的系统，如用于峰值检测、平方运算、正弦波转方波、倍频等功能的电子电路
• 常见的电子失真现象，如削波失真、交越失真和转换速率失真
• 一个信号与另一个信号相乘，如调幅和自动增益控制
• 滞后现象，如铁中磁通密度与磁场强度的关系，或硫化橡胶中机械应力与应变的关系
• 饱和现象，如电子放大器和变压器过载运行
• 具有阈值的系统，例如数字逻辑门，或强度足以粉碎中间岩石的地震振动

线性性的特殊性质

线性性具有交换律特性，这一特性涉及两个或多个系统的组合。图 5-10 展示了其基本概念。设想两个系统以级联方式组合，即一个系统的输出作为下一个系统的输入。若每个系统都是线性的，那么整个组合系统也将是线性的。交换律特性表明，级联系统中各系统的顺序可以重新排列，而不会影响整个组合系统的特性。你可能在电子电路中应用过这一原理。例如，设想一个由两级电路组成的电路，一级用于放大，一级用于滤波。哪种顺序更好，是先放大后滤波，还是先滤波后放大？如果两级电路都是线性的，那么顺序无关紧要，最终结果相同。但需注意，实际电子电路中存在非线性效应，可能会使顺序变得重要，例如：干扰、直流偏移、内部噪声、转换速率失真等。

图 5-8 展示了线性系统理论的下一步发展：多输入与多输出。如果一个系统由线性子系统和信号加法器组成，则无论其输入和/或输出的数量有多少，该系统都是线性的。系统的复杂程度无关紧要，关键在于系统内部不允许存在任何非线性元素。

要理解线性性对于多输入和/或多输出系统的意义，请考虑以下思想实验。首先，在一个输入端施加信号，同时将其他输入端保持为零。这将导致多个输出端以某种信号模式作出响应。接下来，重复该过程，但在另一个不同的输入端施加另一个信号，同时仍将所有其他输入端保持为零。这个第二个输入信号将导致多个输出端出现另一种信号模式。为完成实验，同时将两个信号分别施加到它们各自的输入端。此时，输出端出现的信号将仅仅是当输入信号分别施加时产生的输出信号的叠加（和）。

在线性系统中，乘法的使用常常被误解。这是因为乘法既可以是线性的，也可以是非线性的，具体取决于信号与什么相乘。图 5-9 展示了这两种情况。一个将输入信号与常数相乘的系统是线性的。根据常数大于或小于 1，这个系统是放大器或衰减器。相反，将一个信号与另一个信号相乘则是非线性的。想象一个正弦波与另一个不同频率的正弦波相乘；结果波形显然不是正弦波。

另一种常见的误解涉及电子电路中添加的寄生信号，如直流偏移和热噪声。这些外来信号的添加是线性的还是非线性的？答案取决于污染信号被视为源自何处。如果它们被视为来自系统内部，则该过程是非线性的。这是因为正弦波输入不会产生纯正弦波输出。相反，如果将外来信号视为通过多输入系统的另一个独立输入端从外部进入系统，则该过程就是线性的，因为系统内部仅需进行信号加法。

叠加原理：数字信号处理（DSP）的基石

在处理线性系统时，信号组合的唯一方式是先进行缩放（即信号与常数相乘），然后再进行加法运算。例如，一个信号不能与另一个信号直接相乘。图 5-10 给出了一个示例：三个信号 x0​[n]、x1​[n] 和 x2​[n] 相加，形成第四个信号 x[n]。这种通过缩放和加法来组合信号的过程称为信号合成。

信号分解是合成的逆过程，即将一个信号分解为两个或多个相加的分量。这一过程比合成更为复杂，因为对于任何一个给定信号，都有无数种可能的分解方式。例如，数字 15 和 25 只能通过合成（相加）得到数字 40。相比之下，数字 40 可以分解为：1+39 或 2+38 或 −30.5+60+10.5，等等。

现在，我们来探讨数字信号处理的核心：叠加原理，这是理解信号和系统分析方法的总体策略。考虑一个输入信号 x[n] 通过一个线性系统，产生一个输出信号 y[n]。如图 5-11 所示，输入信号可以分解为一组更简单的信号：x0​[n]、x1​[n]、x2​[n] 等，我们称这些为输入信号分量。接下来，每个输入信号分量分别通过系统，产生一组输出信号分量：y0​[n]、y1​[n]、y2​[n] 等。然后，将这些输出信号分量合成为输出信号 y[n]。

关键点在于：通过这种方法得到的输出信号与直接将输入信号通过系统得到的输出信号完全相同。这是一个非常强大的思想。我们无需试图理解复杂信号如何被系统改变，而只需了解简单信号如何被修改。在信号处理的专业术语中，输入和输出信号被视为更简单波形的叠加（和）。这几乎是所有信号处理技术的基础。

作为叠加原理应用的一个简单示例，请在脑海中将数字 2041 与数字 4 相乘。你是如何做到的？你可能会想象脑海中漂浮着 2041 根火柴，将这一心理图像放大四倍，然后开始计数。但更有可能的是，你使用了叠加原理来简化问题。数字 2041 可以分解为：2000+40+1。每个分量分别乘以 4，然后合成以找到最终答案，即 8000+160+4=8164。

常见信号分解方法

请记住，这种方法的目的是用几个简单问题来替代复杂问题。如果分解不能以某种方式简化情况，那么就毫无意义。在信号处理中，主要有两种信号分解方法：脉冲分解和傅里叶分解。接下来的几章将详细介绍这两种方法。此外，偶尔还会使用几种次要的分解方法。以下是对两种主要分解方法及三种次要分解方法的简要介绍。

脉冲分解

如图 5-12 所示，脉冲分解将一个包含 N 个采样点的信号分解为 N 个分量信号，每个分量信号也包含 N 个采样点。每个分量信号仅包含原始信号中的一个点，其余值均为零。在一串零中，单个非零点被称为脉冲。脉冲分解之所以重要，是因为它允许我们逐个采样点地分析信号。同样，系统也通过其对脉冲的响应来表征。通过了解系统对脉冲的响应，可以计算出系统对任何给定输入的输出。这种方法称为卷积，也是接下来两章的主题。

阶跃分解

如图 5-13 所示，阶跃分解同样将一个包含 N 个采样点的信号分解为 N 个分量信号，每个分量信号也由 N 个采样点组成。每个分量信号都是一个阶跃信号，即前几个采样点的值为零，而后几个采样点为某个常数。考虑将一个 N 点信号 x[n] 分解为分量：x0​[n]、x1​[n]、x2​[n]、……、xN−1​[n]。第 k 个分量信号 xk​[n] 在第 0 到第 k−1 个采样点处为零，而其余采样点的值为：x[k]−x[k−1]。例如，第 5 个分量信号 x5​[n] 在第 0 到第 4 个采样点处为零，而其余采样点的值为：x[5]−x[4]（原始信号中第 4 个和第 5 个采样点之间的差值）。作为一种特殊情况，x0​[n] 的所有采样点都等于 x[0]。正如脉冲分解逐点分析信号一样，阶跃分解通过相邻采样点之间的差值来表征信号。同样，系统也通过其对输入信号变化的响应来表征。

偶/奇分解

如图 5-14 所示，偶/奇分解将一个信号分解为两个分量信号，一个具有偶对称性，另一个具有奇对称性。如果一个 N 点信号关于点 N/2 呈镜像对称，则称该信号具有偶对称性。即，采样点 x[N/2+1] 必须等于 x[N/2−1]，采样点 x[N/2+2] 必须等于 x[N/2−2]，以此类推。同样，当匹配点的大小相等但符号相反时，如：x[N/2+1]=−x[N/2−1]，x[N/2+2]=−x[N/2−2] 等，则称信号具有奇对称性。这些定义假设信号由偶数个采样点组成，且索引从 0 到 N−1。分解可通过以下关系计算得出：这可能看起来是对左右对称性的奇怪定义，因为 N/2−0.5（两个采样点之间）才是信号的精确中心，而不是 N/2。同样，这种非中心对称意味着需要对第 0 个采样点进行特殊处理。

这究竟是怎么回事？
这种分解是数字信号处理中一个重要概念——循环对称性的一部分。它基于将信号的末端视为与信号的起始端相连。正如点 x[4] 紧邻点 x[5] 一样，点 x[N−1] 也紧邻点 x[0]。想象一条蛇咬住自己的尾巴。当以这种循环方式看待偶信号和奇信号时，实际上存在两条对称轴，一条在点 x[N/2]，另一条在点 x[0]。例如，在偶信号中，关于 x[0] 的这种对称性意味着点 x[1] 等于点 x[N−1]，点 x[2] 等于点 x[N−2]，以此类推。在奇信号中，点 0 和点 N/2 的值始终为零。在偶信号中，点 0 和点 N/2 的值等于原始信号中对应点的值。

为什么要将信号的最后一个采样点视为紧邻第一个采样点？
在传统的数据采集中，没有任何依据支持这种循环概念。事实上，第一个和最后一个采样点通常比序列中的其他任意两点之间的共同点更少。这是常识！这个谜题的缺失部分是一种称为傅里叶分析的数字信号处理技术。尽管傅里叶分析的数学原理本质上将信号视为循环的，但这通常在数据的实际来源方面没有物理意义。我们将在第 10 章中更详细地探讨这一点。目前，需要理解的重要一点是，式 5-1 提供了一种有效的分解方法，仅仅因为偶分量和奇分量可以相加来重建原始信号。