区间dp|单调deque
lc863
用前缀和+单调队列,通过两个优化剔除无效元素,快速找到和≥k的最短子数组长度


class Solution {
public:
int shortestSubarray(vector<int> &nums, int k) {
int n = nums.size(), ans = n + 1;
long s[n + 1];
s[0] = 0L;
for (int i = 0; i < n; ++i)
s[i + 1] = s[i] + nums[i]; // 计算前缀和
deque<int> q;
for (int i = 0; i <= n; ++i) {
long cur_s = s[i];
while (!q.empty() && cur_s - s[q.front()] >= k) {
ans = min(ans, i - q.front());
q.pop_front(); // 优化一
}
while (!q.empty() && s[q.back()] >= cur_s)
q.pop_back(); // 优化二
q.push_back(i);
}
return ans > n ? -1 : ans;
}
};
lc218
将建筑端点转成带正负标记的高度对排序
height.push_back({b[0], -b[2]}); // 左端点
height.push_back({b[1], b[2]}); // 右端点
sort(height.begin(), height.end());
用multiset维护当前最大高度,高度变化时记录关键点
if (h.second < 0) // 左端点
st.insert(-h.second);
else // 右端点
st.erase(st.find(h.second));
curMaxHeight = *st.rbegin();
变化- 生成天际线
res.push_back({h.first, curMaxHeight});

class Solution {
public:
vector<vector<int>> getSkyline(vector<vector<int>>& buildings)
{
vector<vector<int>> res;
vector<pair<int, int>> height;
for (auto &b : buildings) {
// 正负用于判别是左端点还是右端点,同时保证排序后:
// 左端点相同时,最高的楼排在前面,insert的一定是相同左端点中最大的高度
// 右端点相同时,最低的楼排在前面,erase的时候不会改变最大高度
height.push_back({b[0], -b[2]}); // 左端点
height.push_back({b[1], b[2]}); // 右端点
}
sort(height.begin(), height.end());
// 维护当前最大高度
multiset<int> st;
st.insert(0); // 保证端点全部删除之后能得到当前最大高度为 0
int preMaxHeight = 0, curMaxHeight = 0;
for (auto &h : height)
{
if (h.second < 0) { // 左端点
st.insert(-h.second);
} else { // 右端点
st.erase(st.find(h.second));
}
curMaxHeight = *st.rbegin();
// 最大高度发生改变,一定是一个 key point,即一个水平线段的左端点
if (curMaxHeight != preMaxHeight) {
res.push_back({h.first, curMaxHeight});
preMaxHeight = curMaxHeight;
}
}
return res;
}
};
lc87
区间dp
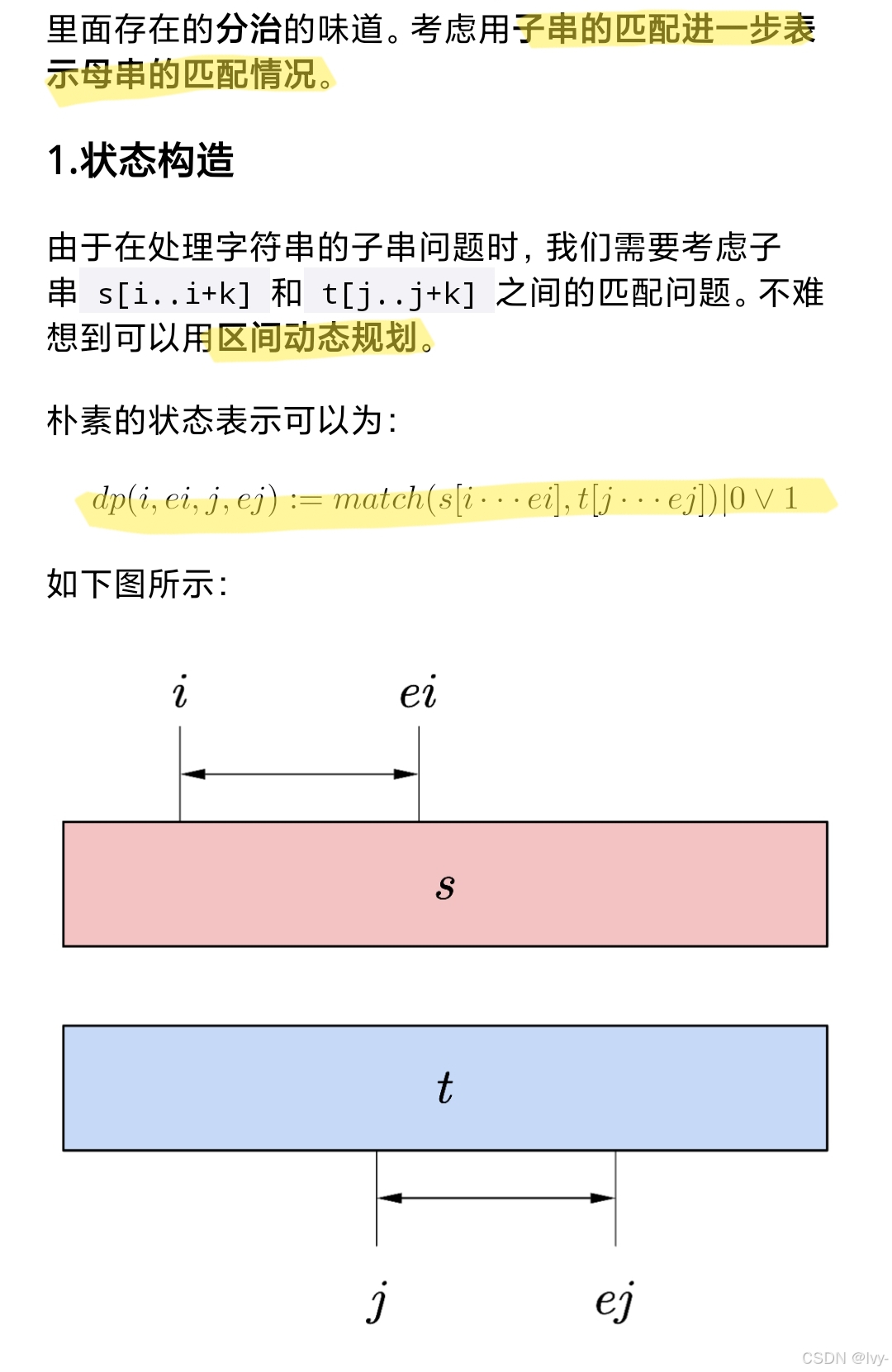
三维DP记录s起始i、t起始j、长度k的子串是否为扰乱串
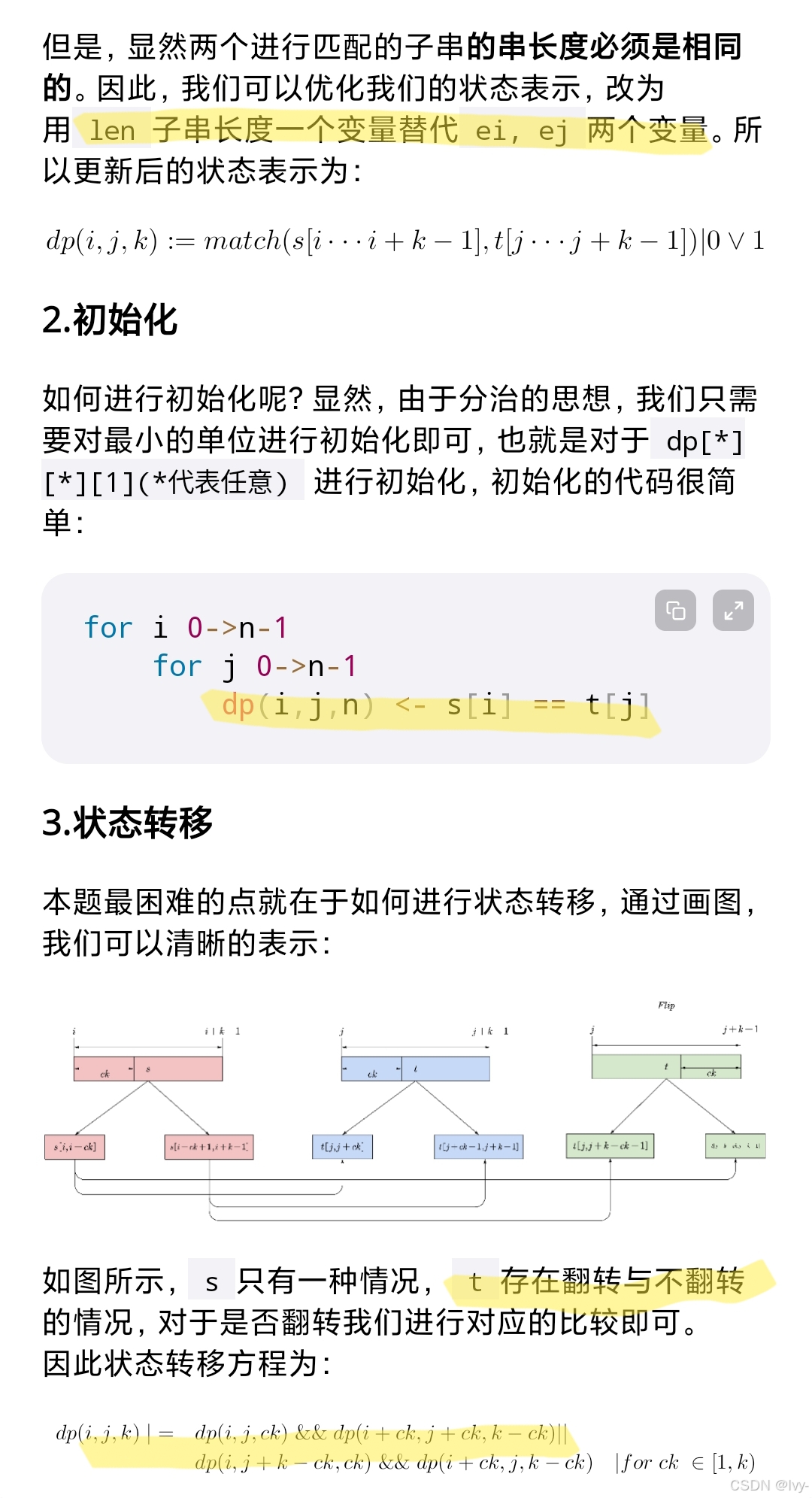
按长度递增枚举,通过拆分+是否交换两种情况判断匹配
dp[i][j][k] |= (
(dp[i][j][ck] && dp[i + ck][j + ck][k - ck]) ||
(dp[i][j + k - ck][ck] && dp[i + ck][j][k - ck])
);
dp[i][j][k]定义“s从i开始、t从j开始、长度为k的子串是否为扰乱串”
题目要判断整个s(i=0开始)和整个t(j=0开始)、长度为n(字符串总长度) 是否匹配
return dp[0][0][n]
#define vt std::vector
class Solution {
public:
bool isScramble(string s, string t) {
if (s.length() != t.length()) return false;
int n = s.length();
vt<vt<vt<int>>> dp(n, vt<vt<int>>(n, vt<int>(n + 1, 0)));
for (int i = 0; i < n; ++ i)
for (int j = 0; j < n; ++ j)
dp[i][j][1] = s[i] == t[j];
for (int k = 2; k <= n; ++ k){
for (int i = 0; i + k <= n; ++ i){
for (int j = 0; j + k <= n; ++ j){
for (int ck = 1; ck < k; ++ ck){
dp[i][j][k] |= (
(dp[i][j][ck] && dp[i + ck][j + ck][k - ck]) ||
(dp[i][j + k - ck][ck] && dp[i + ck][j][k - ck])
);
}
}
}
}
return dp[0][0][n];
}
};
