CVPR2025 | OPS | 通过假设空间增强提升对抗迁移性
Boosting Adversarial Transferability through Augmentation in Hypothesis Space
- 引言-Introduction
- 相关工作-Related Work
- 方法-Methodology
- 预备知识
- 假设空间
- 两大邻域模型增强方案
- OPS攻击算法实现
- 向 3D 点云模态的扩展
- 实验-Experiments
- 实验基础配置
- 图像分类任务评估
- 3D点云分类任务评估
- 消融实验
- 结论-Conclusion
论文链接
GitHub链接
该论文提出 OPS(Operator-Perturbation-based Stochastic Optimization,基于算子扰动的随机优化)方法,核心灵感源于模型泛化能力与对抗样本迁移性的镜像关系,通过在假设空间中对代理模型进行 “模型增强”(输入变换算子组合与随机扰动采样)构建随机优化问题,生成迁移性更强的对抗样本;在图像和 3D 点云 两种模态上验证,OPS 在迁移攻击成功率和计算开销上显著优于现有 SOTA 方法,同时构建了首个 3D 点云迁移攻击基准 3DTAB,为相关研究提供统一评估框架。
引言-Introduction
- 研究背景
- DNN 的广泛应用:深度神经网络(DNNs)已融入众多现实场景,如人脸识别、自动驾驶等,成为核心技术支撑。
- 对抗样本的威胁:存在 “对抗样本” 这一关键问题——向原始数据添加微小扰动,即可误导 DNN 做出错误预测,暴露了 DNN 在关键应用中的脆弱性,因此,研究者对 DNN 相关的对抗攻击与防御策略的关注度日益提升。
- 对抗攻击的核心分类与迁移性问题
- 对抗攻击分类:依据攻击者获取的目标模型信息,对抗攻击分为两类:一是白盒攻击,攻击者可完全获取目标模型参数;二是黑盒攻击,攻击者仅能有限访问目标模型。
- 对抗样本的迁移性:Goodfellow 等人的研究发现,为特定模型生成的对抗样本也可误导其他模型,此现象即 “对抗样本的迁移性”。这使得攻击者可在白盒场景下利用代理模型生成对抗样本,再借助迁移性实施黑盒攻击。
- 迁移性的局限:白盒场景生成的对抗样本常过度拟合代理模型,导致其在白盒攻击中表现良好,但迁移性较差。
- 现有提升迁移性方法的不足
- 现有策略尝试:为增强迁移性,研究者开发了多种策略,包括稳定梯度方向、寻找平坦损失解、增加输入多样性、修改前向或反向过程、添加正则化项等。
- 方法的缺陷:这些方法往往引入复杂计算,同时仅能带来相对有限的性能提升,难以满足实际应用需求。
- 本文核心思路与方法提出
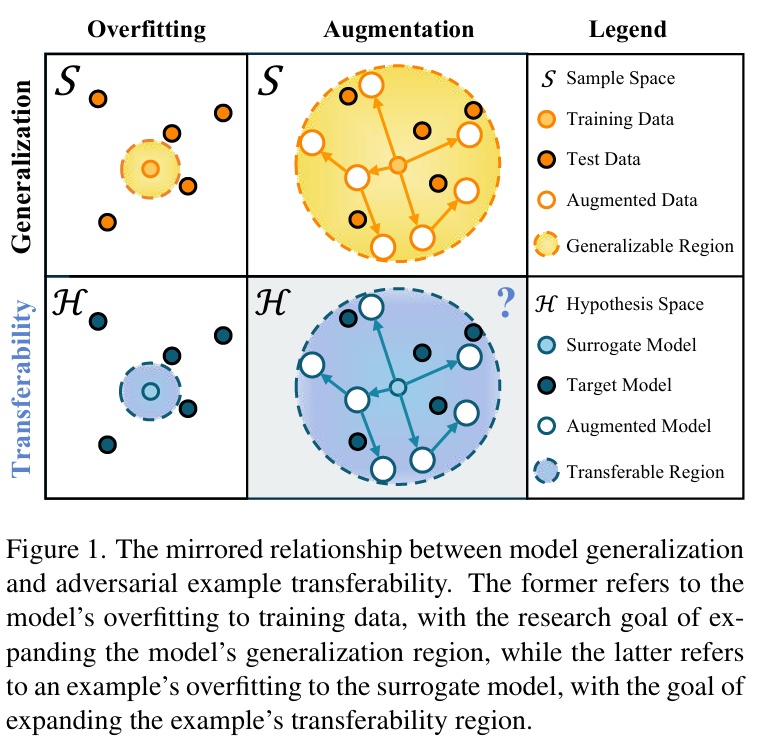
- 关键观察:引入机器学习中的 “样本空间” 与 “假设空间” 作为数据和模型的通用集合,忽略数据与模型间的交互细节后,发现模型泛化性研究与迁移性研究存在镜像关系——模型泛化性研究旨在扩展样本空间内模型的可泛化区域,迁移性研究则旨在扩展假设空间内对抗样本的可迁移区域。
- 方法灵感与设计:受数据增强提升模型泛化性的启发,思考能否对代理模型进行 “模型增强” 以提升迁移性。进一步分析认为,目标模型位于代理模型在假设空间中的邻域内,理想的增强方式是采样代理模型邻域以获取更多模型,但直接采样假设空间中代理模型的邻域存在挑战。
- OPS 方法提出:为解决上述采样难题,提出两种简单替代方案——将代理模型与输入变换算子组合,或与固定扰动结合,再利用所得的邻域模型构建随机优化问题,通过求解该问题生成迁移性更优的对抗样本,将此方法命名为“基于算子扰动的随机优化(OPS)”。
- 本文研究范围与核心贡献
- 模态验证范围:通过替换输入变换算子,OPS 可轻松适配不同模态,本文聚焦视觉领域,在图像和 3D 点云两种视觉模态上验证 OPS 的有效性;同时,鉴于目前缺乏公开的 3D 点云基准,构建了 “3D迁移攻击基准(3DTAB)” 以全面评估方法。
- 核心贡献:从重新审视对抗样本迁移性、提出 OPS 攻击方法、建立 3D 点云基准、通过实验验证 OPS 优越性四个方面,明确了本文的核心贡献方向。
相关工作-Related Work
- 图像领域的基于迁移的攻击
- 基于梯度的方法:以优化梯度方向或损失景观为核心,旨在缓解对抗样本对代理模型的过拟合。
- 早期方法:迭代版本 I-FGSM 虽白盒攻击性能较优,但迁移性较低;MI 提出动量技术解决 I-FGSM 陷入局部最优的问题,后续衍生出NI、VMI、GRA 等动量类攻击方法。
- 平坦损失解方法:RAP 通过搜索平坦损失景观的对抗样本来提升迁移性,但需额外计算开销;后续 PGN、NCS 部分解决了计算问题,实现了更高迁移性。
- 输入变换基方法:通过增强输入多样性提升迁移性,是当前主流方向之一。
- 基础思路:DIM 首次提出通过随机调整图像尺寸后填充至固定大小的方式增强多样性,后续方法多在此基础上优化。
- 代表性方法:SIM 引入尺度缩放变换;Admix、DeCoWA 探索更优变换组合;SIA、BSR 将图像分解为块并对块施加不同变换,进一步提升多样性;AITL 用网络预测最优变换组合,L2T 为每个样本学习最优变换轨迹,实现 “定制化” 变换。
- OPS 与现有方法的差异:OPS 虽使用输入变换,但既不追求增强输入多样性,也不为单个样本定制变换,而是通过每次迭代随机选择变换来增强梯度多样性,最终实现更高计算效率。
- 基于梯度的方法:以优化梯度方向或损失景观为核心,旨在缓解对抗样本对代理模型的过拟合。
- 图像领域的对抗防御
- 对抗训练:将对抗样本融入训练集以提升模型鲁棒性,是最直接的防御手段之一。比如利用不同模型生成的对抗样本进行集成对抗训练,有效提升了模型对基于迁移的攻击的抵抗能力。
- 输入净化:通过恢复对抗样本至自然样本状态实现防御,核心是 “去除对抗扰动”。例如通过训练高维表示引导去噪器(HGD),专门用于移除对抗样本中的噪声。
- 认证防御:在特定扰动半径内提供可证明的鲁棒性保证,区别于经验性防御。例如基于随机平滑(RS)训练 ImageNet 分类器,明确给出了可证明的防御半径。
- 3D点云领域的对抗攻击研究
- 3D点云对抗攻击的发展:
- 起步阶段:3D-Adv 基于 C&W 攻击,是首个 3D 点云对抗攻击研究,后续方法多围绕 “生成更自然、人类难察觉的对抗样本” 优化。
- 优化方向:KNN 将 K 近邻距离融入损失函数;GeoA³ 提出几何感知损失项;HiT-ADV 引入不可感知分数,控制人类视觉不敏感区域的扰动,降低对抗样本的可察觉性。
- 迁移性优化:AdvPC 指出早期方法生成的对抗样本易过拟合特定模型、迁移性差,进而引入点云重建对抗损失缓解过拟合;后续 AOF 针对低频分量引入对抗损失,PF-Attack 针对子扰动引入对抗损失,均延续了 “损失优化提升迁移性” 的思路。
- 3D点云对抗防御的发展:
- 防御策略的通用性:多数 2D 防御方法无法直接应用于3D任务,但防御核心思路具有通用性。
- 代表性防御方法:Liu 等人将对抗训练扩展到 3D 领域;Zhou 等人发现对抗点云常含异常值,提出 SRS、SOR 两种简单输入净化方法,并设计 DUP-Net 提升防御效果;IFDefense 聚焦 3D 物体的隐式函数表示,利用占据网络从受攻击点云中恢复干净点云;Liu 等人基于随机采样,提出首个 3D 点云认证防御方法。
- 3D点云对抗攻击的发展:
方法-Methodology
预备知识
- 模态适用性:以图像分类任务为例阐述算法设计思路,但方法不局限于图像模态,可扩展至 3D 点云。
- 核心定义:明确 “代理模型” 与 “目标模型”,并定义对抗样本需满足两大特性:一是 “对抗性”,即能误导目标模型;二是 “不可感知性”,即人类难以区分对抗样本与原始样本。
- 白盒攻击优化问题:白盒场景下,对抗样本生成被建模为盒约束优化问题,目标是在原始样本 xorix^{ori}xori 的 ℓ∞\ell_\inftyℓ∞ 邻域内(扰动预算 ϵ\epsilonϵ),最大化代理模型 fθf_\thetafθ 的交叉熵损失 J(fθ(xadv),y)\mathcal{J}(f_\theta(x^{adv}), y)J(fθ(xadv),y),公式如下:
argmaxxadvJ(fθ(xadv),y)s.t.∥xadv−xori∥∞<ϵ\begin{array}{rl}{\underset {x^{adv}}{arg max } }{\mathcal {J}\left(f_{\theta }\left(x^{adv}\right) , y\right) } \quad {s.t. }{\left\| x^{adv}-x^{ori }\right\| _{\infty }<\epsilon }\end{array}xadvargmaxJ(fθ(xadv),y)s.t.xadv−xori∞<ϵ
实际优化中以扰动 Δ=xadv−xori\Delta=x^{adv}-x^{ori}Δ=xadv−xori为变量,通过迭代更新(如 I-FGSM 的 Δi+1=Δi+Clipϵ{α⋅Sign(∇xJ(fθ(xori+Δi),y))}\Delta_{i+1}=\Delta_i+Clip_\epsilon\{\alpha\cdot Sign(\nabla_x\mathcal{J}(f_\theta(x^{ori}+\Delta_i),y))\}Δi+1=Δi+Clipϵ{α⋅Sign(∇xJ(fθ(xori+Δi),y))})求解,其中 ClipϵClip_\epsilonClipϵ 为裁剪超预算扰动的操作,α=ϵ/T\alpha=\epsilon/Tα=ϵ/T(TTT 为迭代次数)。 - 迁移攻击优化问题:迁移场景下(代理模型≠目标模型,目标模型集为 V={f1,f2,...}V=\{f_1,f_2,...\}V={f1,f2,...}),优化目标变为最大化对抗样本在目标模型集上的期望损失 Efi∈V[J(fi(xadv),y)]\mathbb{E}_{f_i \in V}[\mathcal{J}(f_i(x^{adv}),y)]Efi∈V[J(fi(xadv),y)],但因攻击者无法获取目标模型集信息,该问题难以直接求解,进而引出 “模型增强” 的思路。
假设空间
- 假设空间定义:将 MMM 类图像分类任务的神经网络表示为函数 h:x→zh:x \to zh:x→z(x∈RH×W×Cx \in \mathbb{R}^{H×W×C}x∈RH×W×C 为输入图像,z∈RMz \in \mathbb{R}^Mz∈RM 为预测分数),假设空间 H\mathcal{H}H 为所有此类函数的集合。
- 性能量化与伪度量:定义泛函 F(h)=∫J(h(x),y)⋅p(x)dx\mathcal{F}(h)=\int \mathcal{J}(h(x),y)\cdot p(x)dxF(h)=∫J(h(x),y)⋅p(x)dx(p(x)p(x)p(x) 为输入数据分布)量化假设 h∈Hh \in \mathcal{H}h∈H 的性能,进而定义伪度量 d(h1,h2)=∣F(h1)−F(h2)∣d(h_1,h_2)=|\mathcal{F}(h_1)-\mathcal{F}(h_2)|d(h1,h2)=∣F(h1)−F(h2)∣ 衡量两个假设的差异。
- 邻域与核心洞察:以伪度量为基础,定义以代理模型 fθf_\thetafθ 为中心、半径 rrr 的邻域 Br(fθ)={h′∣d(fθ,h′)<r}\mathcal{B}_r(f_\theta)=\{h' | d(f_\theta,h')<r\}Br(fθ)={h′∣d(fθ,h′)<r}。核心洞察为:代理模型与目标模型均为高性能分类模型,故二者同属集合 H={h∣F(h)<a}\mathcal{H}=\{h | \mathcal{F}(h)<a\}H={h∣F(h)<a}(aaa 为小值),即目标模型集 V⊂Ba(fθ)V \subset \mathcal{B}_a(f_\theta)V⊂Ba(fθ),因此可通过采样代理模型邻域内的模型近似目标模型分布,将迁移攻击优化问题替换为:
argmaxxadvEh∈Ba(fθ)[J(h(xadv),y)]\underset{x^{adv}}{arg max } \mathbb{E}_{h \in \mathcal{B}_a(f_\theta)}\left[\mathcal{J}\left(h\left(x^{adv}\right), y\right)\right]xadvargmaxEh∈Ba(fθ)[J(h(xadv),y)]
但因假设空间为函数空间,直接采样邻域模型存在挑战,故提出两种间接增强方案。
两大邻域模型增强方案
- 算子采样(Operator Sampling)
- 核心思路:通过 “代理模型+输入变换算子” 的复合构建邻域模型,即 f′=fθ∘opf'=f_\theta \circ opf′=fθ∘op,其中 op:RH×W×C→RH×W×Cop: \mathbb{R}^{H×W×C} \to \mathbb{R}^{H×W×C}op:RH×W×C→RH×W×C 为输入变换算子,∘\circ∘ 表示函数复合。
- 算子集构建:
- 基础算子集 Pb\mathcal{P}_bPb:选择对代理模型扰动较小的变换算子(如图像的缩放、裁剪,3D点云的刚体变换);
- k 阶扩展集 Pbk\mathcal{P}_b^kPbk:通过算子复合扩展算子数量,定义为 Pbk={op1∘op2∘⋯∘opk∣op1,...,opk∈Pb}\mathcal{P}_b^k=\{op_1 \circ op_2 \circ \cdots \circ op_k | op_1,...,op_k \in \mathcal{P}_b\}Pbk={op1∘op2∘⋯∘opk∣op1,...,opk∈Pb}(Pb1=Pb\mathcal{P}_b^1=\mathcal{P}_bPb1=Pb);
- 最终算子集 P\mathcal{P}P:引入阶数列表 KlistK_{list}Klist 指定扩展集阶数,从每个扩展集中随机采样 ∣Pb∣|\mathcal{P}_b|∣Pb∣ 个算子(记为 S(A,n)S(A,n)S(A,n),表示从集合 AAA 中采样 nnn 次),即 P=⋃k∈KlistS(Pbk,∣Pb∣)\mathcal{P}=\bigcup_{k \in K_{list}} S(\mathcal{P}_b^k,|\mathcal{P}_b|)P=⋃k∈KlistS(Pbk,∣Pb∣),确保不同阶数算子数量平衡。
- 算子集构建:
- 采样策略:每次迭代从 P\mathcal{P}P 中随机选择 NpN_pNp 个算子用于增强。
- 核心思路:通过 “代理模型+输入变换算子” 的复合构建邻域模型,即 f′=fθ∘opf'=f_\theta \circ opf′=fθ∘op,其中 op:RH×W×C→RH×W×Cop: \mathbb{R}^{H×W×C} \to \mathbb{R}^{H×W×C}op:RH×W×C→RH×W×C 为输入变换算子,∘\circ∘ 表示函数复合。
- 扰动采样(Perturbation Sampling)
- 核心思路:通过 “输入+随机扰动” 的方式构建邻域模型,即 f′(x)=fθ(x+δ)f'(x)=f_\theta(x+\delta)f′(x)=fθ(x+δ)(δ\deltaδ 为输入扰动),该方式满足 Lipschitz 条件(若 fθf_\thetafθ 满足 Lipschitz 条件,则 d(fθ,f′)≤C⋅δd(f_\theta,f') \leq C\cdot\deltad(fθ,f′)≤C⋅δ,CCC 为固定常数),可保证邻域模型的有效性。
- 扰动集构建:引入半径列表 RlistR_{list}Rlist 指定多个开球半径,每个开球定义为 Br={δ∣∥δ∥∞<r}\mathcal{B}_r=\{\delta | \|\delta\|_\infty < r\}Br={δ∣∥δ∥∞<r},从每个开球中均匀采样 NeN_eNe 个扰动,组成扰动集 D=⋃r∈RlistS(Br,Ne)\mathcal{D}=\bigcup_{r \in R_{list}} S(\mathcal{B}_r,N_e)D=⋃r∈RlistS(Br,Ne).
- 采样策略:每次迭代从 D\mathcal{D}D 中随机选择 NeN_eNe 个扰动用于增强。
OPS攻击算法实现
- 优化目标修正:结合算子采样与扰动采样,将迁移攻击的优化目标最终修正为:
argmaxxadvE(D,P)E(δ,op)∈D×P[J(fθ(op(xadv+δ)),y)]\underset{x^{adv}}{arg max } \mathbb{E}_{(\mathcal{D},\mathcal{P})} \mathbb{E}_{(\delta, op) \in \mathcal{D} × \mathcal{P}}\left[\mathcal{J}\left(f_{\theta}\left(op\left(x^{adv}+\delta\right)\right), y\right)\right]xadvargmaxE(D,P)E(δ,op)∈D×P[J(fθ(op(xadv+δ)),y)] - 算法流程:
- 初始化参数:攻击预算 ϵ\epsilonϵ、迭代次数 TTT、衰减因子 μ\muμ、阶数列表 KlistK_{list}Klist、半径列表 RlistR_{list}Rlist、算子采样数 NpN_pNp、扰动采样数 NeN_eNe,计算步长 α=ϵ/T\alpha=\epsilon/Tα=ϵ/T,初始化动量 m0=0m_0=0m0=0、扰动 Δ0=0\Delta_0=0Δ0=0;
- 迭代更新(共 TTT 次):
- 计算原始梯度 gˉ=∇xJ(f(xori+Δi),y)\bar{g}=\nabla_x\mathcal{J}(f(x^{ori}+\Delta_i),y)gˉ=∇xJ(f(xori+Δi),y);
- 构建算子集 P\mathcal{P}P 和扰动集 D\mathcal{D}D;
- 遍历采样的 NeN_eNe 个扰动和 NpN_pNp 个算子,累加梯度 gˉ=gˉ+∇xJ(f(op(xori+Δi+δ)),y)\bar{g}=\bar{g}+\nabla_x\mathcal{J}(f(op(x^{ori}+\Delta_i+\delta)),y)gˉ=gˉ+∇xJ(f(op(xori+Δi+δ)),y);
- 计算平均梯度 gˉ=gˉ/(Ne×Np+1)\bar{g}=\bar{g}/(N_e×N_p+1)gˉ=gˉ/(Ne×Np+1),更新动量 mi+1=μ⋅mi+gˉ/∥gˉ∥1m_{i+1}=\mu\cdot m_i + \bar{g}/\|\bar{g}\|_1mi+1=μ⋅mi+gˉ/∥gˉ∥1;
- 裁剪并更新扰动 Δi+1=Δi+Clipϵ{α⋅Sign(mi+1)}\Delta_{i+1}=\Delta_i + Clip_\epsilon\{\alpha\cdot Sign(m_{i+1})\}Δi+1=Δi+Clipϵ{α⋅Sign(mi+1)};
- 输出对抗样本 xadv=xori+ΔTx^{adv}=x^{ori}+\Delta_Txadv=xori+ΔT.
- 计算开销标识:算法的计算开销主要来自反向传播,次数为 T⋅(Np⋅Ne+1)T·(N_p·N_e+1)T⋅(Np⋅Ne+1),故用 OPS(T,Np,Ne)\text{OPS}(T,N_p,N_e)OPS(T,Np,Ne) 标识不同参数配置的 OPS 算法。

向 3D 点云模态的扩展
- 模态适配核心:OPS 方法的模态扩展性源于 “基础算子集 Pb\mathcal{P}_bPb 的定制化”——图像版本 OPSimg\text{OPS}_{img}OPSimg 的 Pb\mathcal{P}_bPb 包含常用数据增强、SIM 的尺度缩放、DIM 的随机 resize-padding;3D 点云版本 OPSpcOPS_{pc}OPSpc 的 Pb\mathcal{P}_bPb 因现有研究限制,主要采用刚体变换(平移、旋转、缩放)。
- 参数微调:OPSpc\text{OPS}_{pc}OPSpc 的其他参数(如 T,Np,Ne,μT,N_p,N_e,\muT,Np,Ne,μ)与 OPSimg\text{OPS}_{img}OPSimg 一致,仅调整半径列表 RlistR_{list}Rlist 以适配 3D 点云的空间特性。
实验-Experiments
实验基础配置
- 评估基准:图像模态(OPSimgOPS_{img}OPSimg)使用公开基准 TransferAttack 评估;3D 点云模态(OPSpcOPS_{pc}OPSpc)因无公开基准,自行构建3D迁移攻击基准(3DTAB)。
- 实验环境:工作站搭载 Intel i9-10980XE(36核,4.600GHz)、128GB 内存,GPU 为 RTX 3090,确保实验计算资源一致性。
图像分类任务评估
- 实验设置
- 数据集:遵循现有研究,从 ImageNet 数据集验证集中选取 1000 张图像;攻击批量大小统一设为 32.
- 评估模型:
- 正常训练模型:8 种主流架构,包括 ResNet-18、ResNet-101、ResNeXt-50、DenseNet-121、ViT、PiT、Visformer、Swin,均在 ImageNet 上预训练。
- 鲁棒模型:覆盖 3 类防御策略,共 5 种方法,包括对抗训练、基于随机平滑(RS)的认证防御、输入净化(HGD、NRP)。
- 基线方法:分为两类对比——基于梯度的方法(VMI、GRA、PGN、NCS)、基于输入变换的方法(DeCoWA、SIA、BSR、L2T),所有基线参数均与原论文保持一致。
- OPS参数:
- 随机优化参数:阶数列表 Klist=[1,2,3,4]K_{list}=[1,2,3,4]Klist=[1,2,3,4],半径列表 Rlist=[0.5,1.0,1.5,2.0,2.5,3.0]×ϵR_{list}=[0.5,1.0,1.5,2.0,2.5,3.0]×\epsilonRlist=[0.5,1.0,1.5,2.0,2.5,3.0]×ϵ,默认 Ne=Np=5N_e=N_p=5Ne=Np=5.
- 优化求解参数:遵循 MI 默认设置,攻击预算 ϵ=16\epsilon=16ϵ=16(即 16/25516/25516/255),迭代次数 T=10T=10T=10,步长 α=1.6\alpha=1.6α=1.6,衰减因子 μ=1\mu=1μ=1.
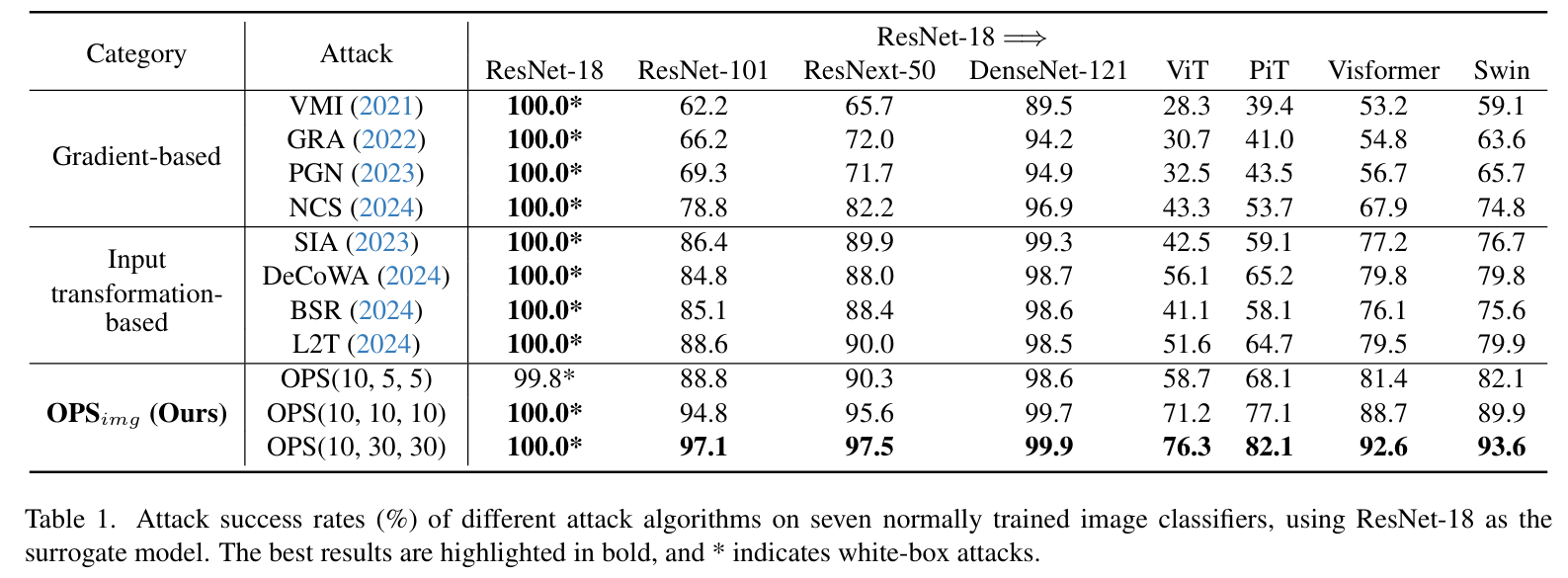
- 正常训练模型评估结果
- 核心结论:OPSimg\text{OPS}_{img}OPSimg 在所有目标模型上均实现最高迁移性,即使轻量配置(OPS(10,5,5)\text{OPS}(10,5,5)OPS(10,5,5))也优于所有基线方法。
- 跨架构攻击:OPSimg\text{OPS}_{img}OPSimg 攻击成功率(ASR)超75%,远超其他方法。
- 高性能配置表现:OPS(10,30,30)\text{OPS}(10,30,30)OPS(10,30,30) 均为所有方法中最优。
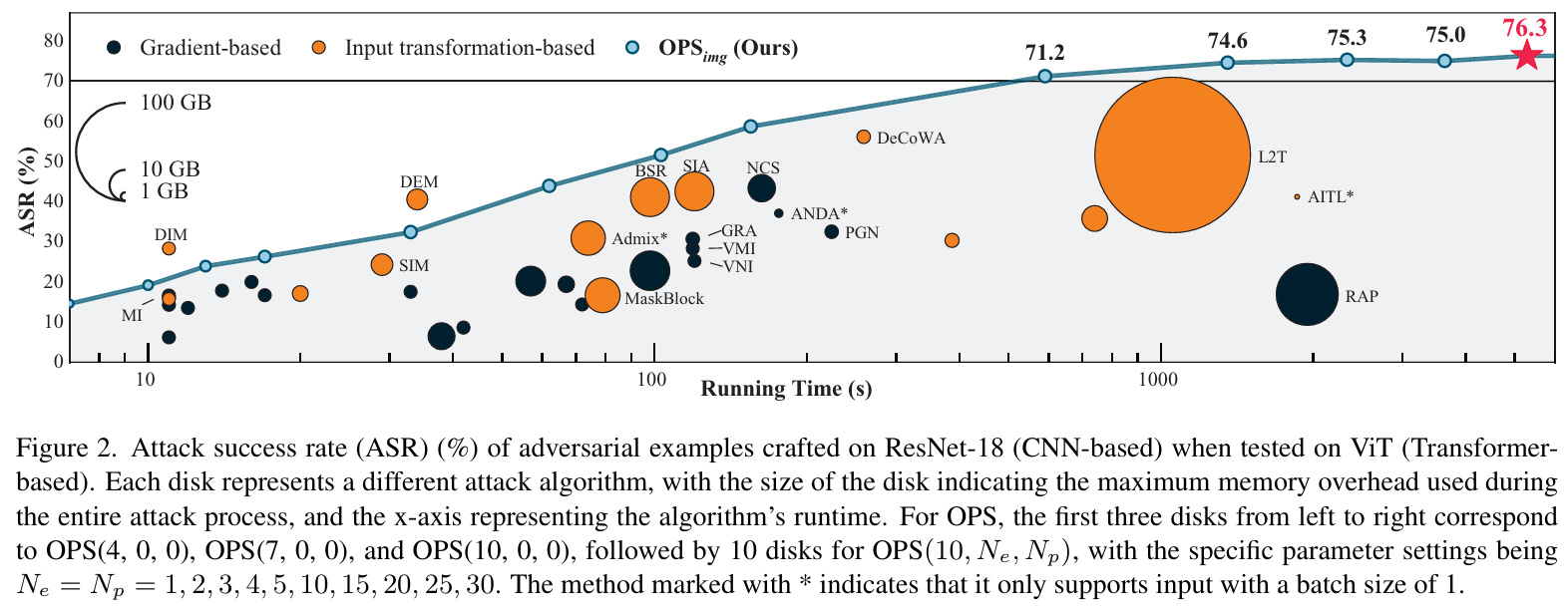
- 性能与成本平衡:图2显示,在 ResNet-18→ViT 场景中,OPSimg\text{OPS}_{img}OPSimg 在相同运行时间下 ASR 更高,且内存开销可控。
- 核心结论:OPSimg\text{OPS}_{img}OPSimg 在所有目标模型上均实现最高迁移性,即使轻量配置(OPS(10,5,5)\text{OPS}(10,5,5)OPS(10,5,5))也优于所有基线方法。
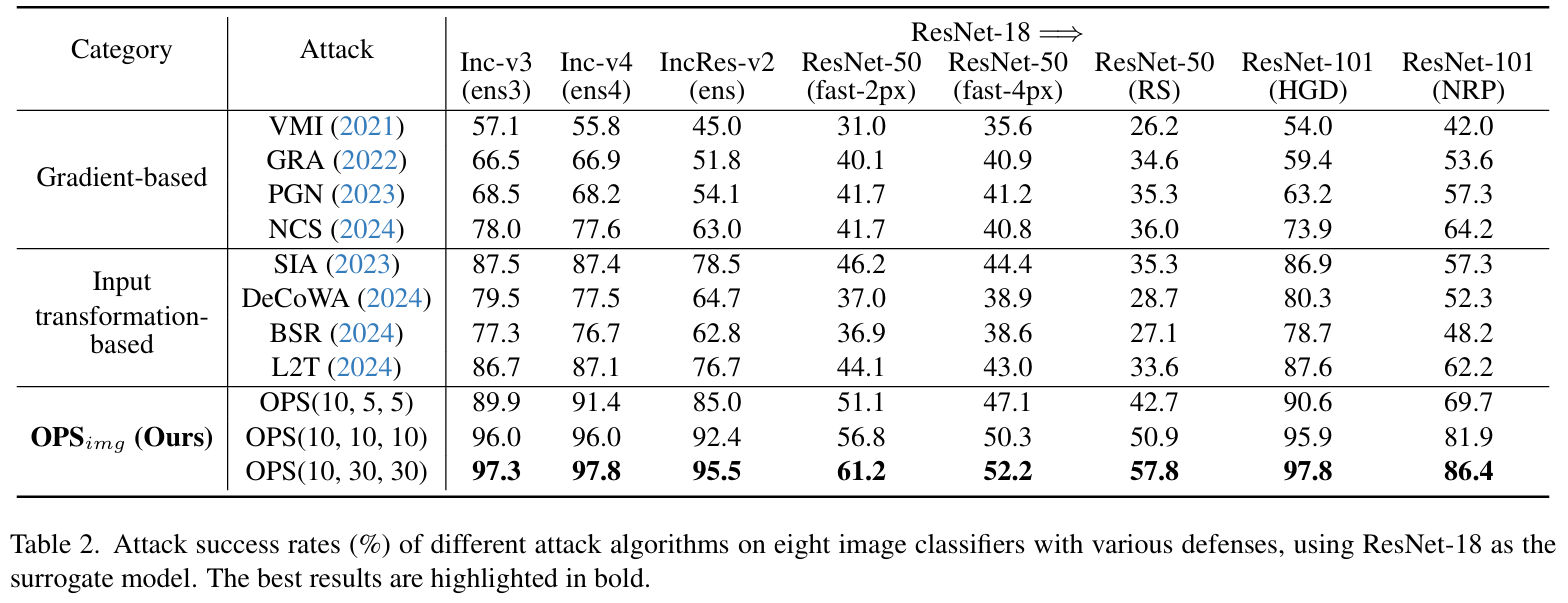
- 鲁棒模型评估结果
- 核心结论:OPSimg\text{OPS}_{img}OPSimg 在各类鲁棒模型上仍保持最高迁移性,验证了方法的实用性。
- 实验分析
- 算子有效性影响:当 NpN_pNp 较小时,OPSimg\text{OPS}_{img}OPSimg 可能因未采样到 DIM 类高效算子导致性能低于 DIM,但 OPSimg\text{OPS}_{img}OPSimg 性能上限更高(随 NpN_pNp 增加 ASR 持续提升),为后续方法评估提供参考依据。
3D点云分类任务评估
- 实验设置
- 数据集:使用预处理后的 ModelNet40 数据集,区别于现有研究(仅 250 个测试样本),将测试样本扩展至 1000 个(每类随机选取 25 个),提升评估可靠性。
- 评估模型:
- 正常训练模型:9 种架构,包括 PointNet、DGCNN、PointConv、PointCNN、CurveNet、PT-v1、PT-v2、RSCNN、Point-PN.
- 鲁棒模型:2 种经典防御方法,DUP-Net(输入净化)、IF-Defense(隐式函数恢复)。
- 基线方法:分为两类——白盒攻击(KNN、GeoA³、HiT-ADV)、迁移攻击(AdvPC、AOF、PF-Attack]),参数与原论文一致。
- OPS 参数:除半径列表 Rlist=[0.5,0.75,1.0,1.25]×ϵR_{list}=[0.5,0.75,1.0,1.25]×\epsilonRlist=[0.5,0.75,1.0,1.25]×ϵ(适配3D点云特性)外,其余参数与 OPSimg\text{OPS}_{img}OPSimg 一致;扰动范数约束为每个点小于 0.18。
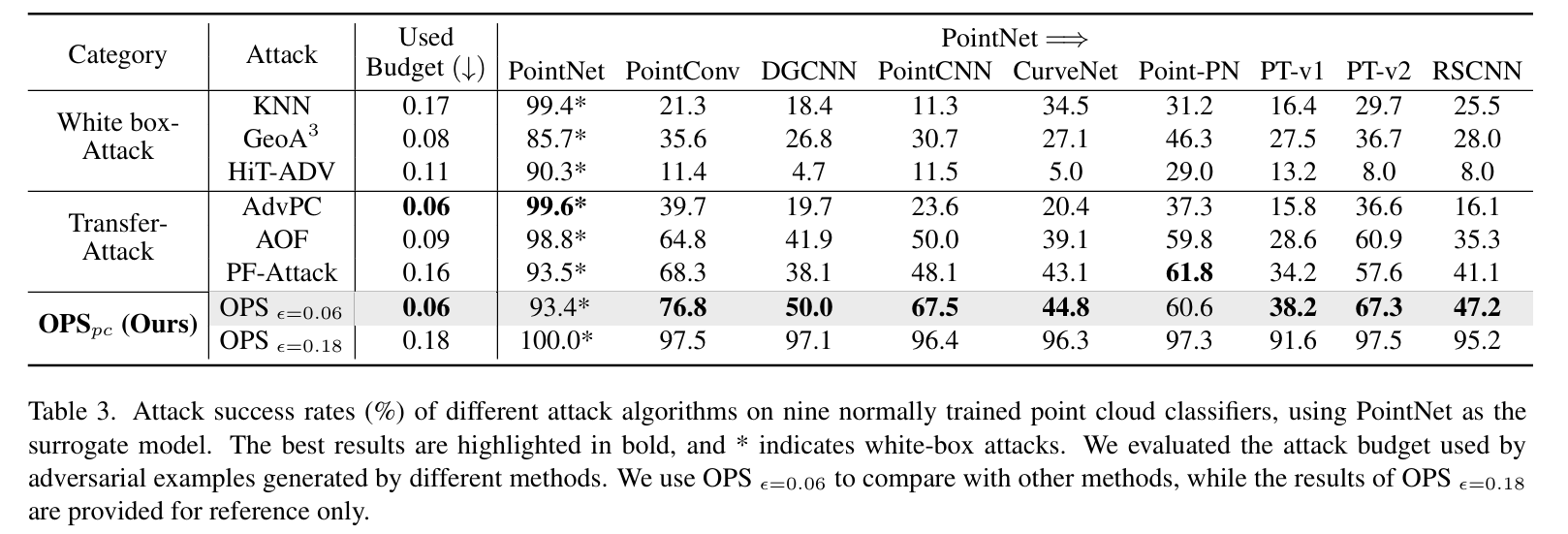
- 正常训练模型评估结果
- 核心结论:OPSpcOPS_{pc}OPSpc 在预算利用效率和迁移性上均优于基线。
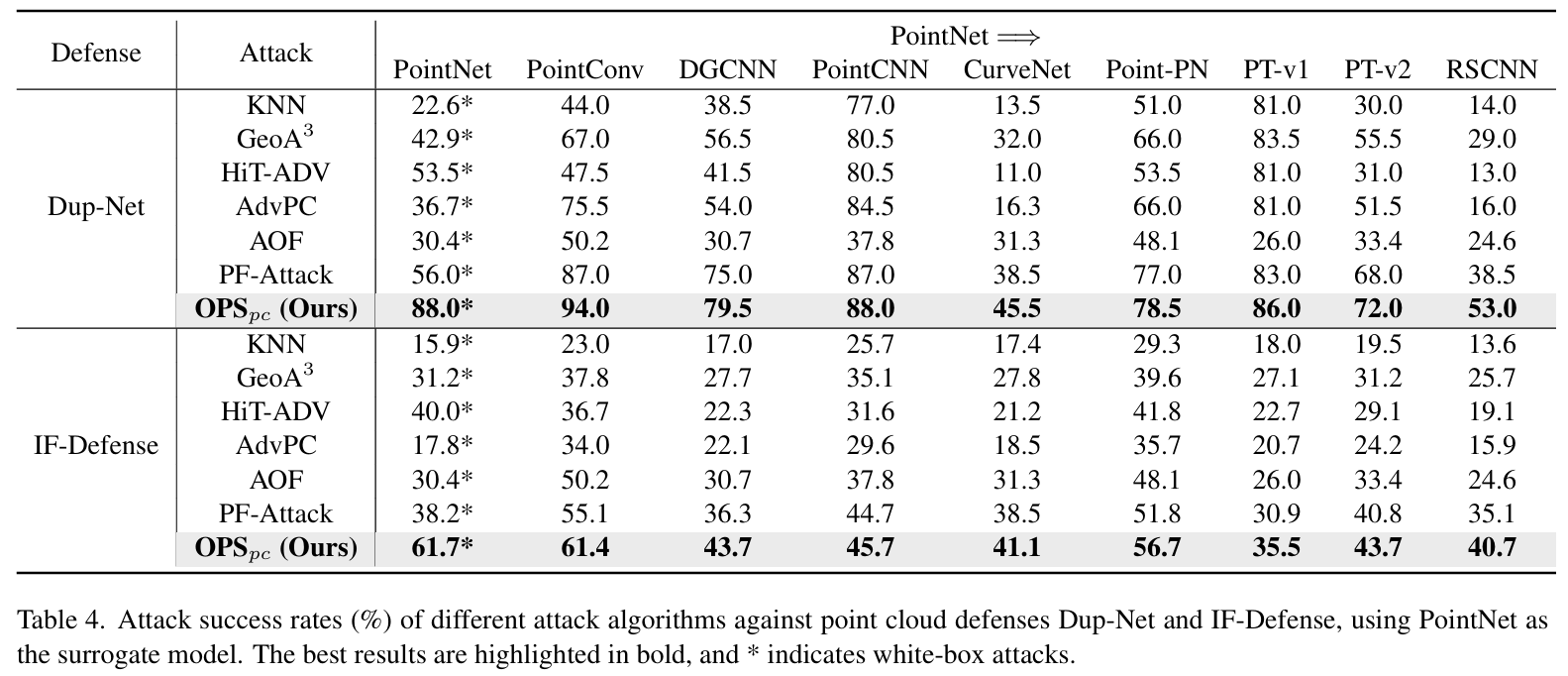
- 鲁棒模型评估结果
- 核心结论:OPSpcOPS_{pc}OPSpc 在 DUP-Net 和 IF-Defense 防御下仍保持最优性能。
- 特殊现象分析:DUP-Net 防御下部分模型 ASR 上升,可能因 DUP-Net 的上采样操作(将点云数量增至原始 4 倍)改变点云邻域信息,干扰模型预测。
消融实验
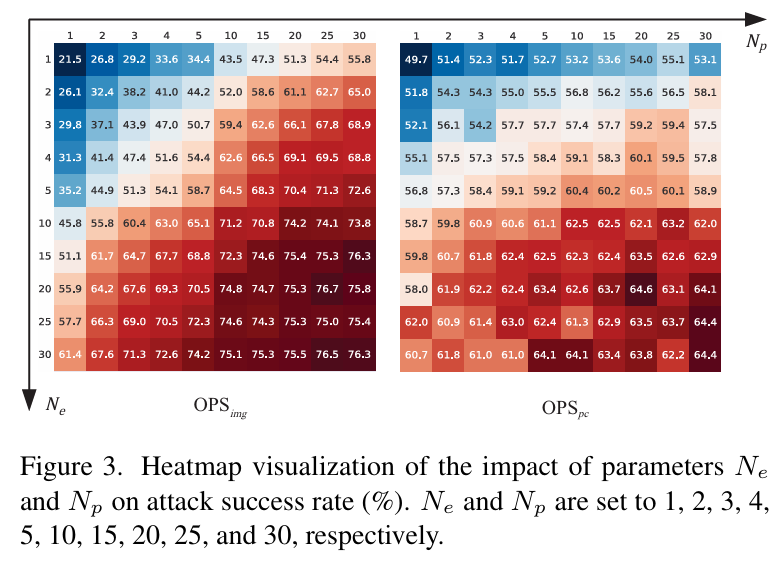
- 参数 NeN_eNe 与 NpN_pNp 的影响
- 实验场景:OPSimg\text{OPS}_{img}OPSimg 选取 ResNet-18→ViT,OPSpc\text{OPS}_{pc}OPSpc 选取 PointNet→PT-v1;NeN_eNe 与 NpN_pNp 均设为1、2、3、4、5、10、15、20、25、30。
- 核心结论:
- OPSimg\text{OPS}_{img}OPSimg:随 NeN_eNe 和 NpN_pNp 增加,迁移性持续提升,约在 20 时达到平台期;两者无显著优先级,计算负载相近时调整任一参数对结果影响微小,故实际应用中设 Ne=NpN_e=N_pNe=Np。
- OPSpc\text{OPS}_{pc}OPSpc:趋势与 OPSimg\text{OPS}_{img}OPSimg 相似,但 NeN_eNe 提升带来的 ASR 增益大于 NpN_pNp,可能因 OPSpc\text{OPS}_{pc}OPSpc 的基础算子集(以刚体变换为主)同质化,导致算子采样的多样性不足。
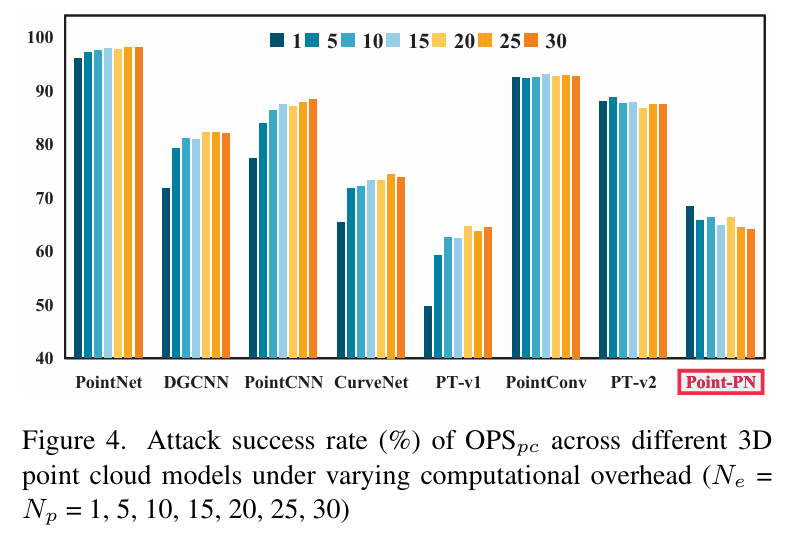
- 计算成本对跨架构攻击的影响
- 实验设置:OPSpc\text{OPS}_{pc}OPSpc 在 PointNet→各目标模型场景中,调整 Ne=Np=1,5,10,15,20,25,30N_e=N_p=1,5,10,15,20,25,30Ne=Np=1,5,10,15,20,25,30 以改变计算开销。
- 核心结论:
- 多数模型:ASR 随计算开销增加稳步上升,后在上限附近波动,符合 “更多采样→更优近似目标模型分布” 的逻辑。
- 特殊模型(Point-PN):ASR 随计算开销增加而下降,因 Point-PN 为参数无关的 3D 点云模型,设计上与其他模型差异显著,该现象为新型防御方法提供启发。
结论-Conclusion
- 核心研究发现:明确观察到模型泛化能力研究与对抗样本迁移性研究之间存在镜像关系,即模型泛化旨在扩展样本空间内的模型可泛化区域,而对抗迁移性旨在扩展假设空间内的对抗样本可迁移区域,为提升迁移性提供了新的理论视角。
- 方法设计逻辑:基于上述镜像关系,探索了在假设空间中对代理模型进行 “增强” 以提升对抗样本迁移性的可行性,最终设计出OPS(基于算子扰动的随机优化)方法——通过输入变换算子与随机扰动两种方式对代理模型进行增强,构建随机优化问题并求解,生成迁移性更优的对抗样本。
- 实验验证结论:在图像(ImageNet 数据集)和 3D 点云(ModelNet40 数据集)两种模态上的大量实验表明,与现有最优攻击方法相比,OPS 在对抗样本迁移性(如跨架构、鲁棒模型场景下攻击成功率显著更高)和计算效率(反向传播次数可控,内存开销更低)两方面均具备显著优势。
- 研究价值与展望:通过将研究视角从数据与模型的局部交互转向二者的全局关系(样本空间与假设空间的对应),揭示了迁移性与泛化能力的内在关联,为后续对抗攻击与防御研究提供了新的思路与方向。
