「用Python来学微积分」8. 极限的概念
极限理论是微积分的基石,它描述了函数在自变量特定变化趋势下的行为规律。本文将系统介绍六种自变量变化趋势,并通过严格的数学定义和Python示例帮助读者直观理解极限概念。
一、极限的基本思想与历史背景
极限概念的核心思想是"无限接近但永不达到"的动态过程。最初牛顿和莱布尼茨以无穷小概念为基础建立了微积分,但遇到了逻辑困难,后来在晚期都不同程度地接受了极限思想。
1.1 极限思想的演变
起初的极限观念建立在几何直观上,缺乏严格的表述。牛顿用"路程的改变量ΔS与时间的改变量Δt之比"表示运动物体的平均速度,让Δt无限趋近于零,得到物体的瞬时速度,并由此引出导数概念和微分学理论。
正因为当时缺乏严格的极限定义,微积分理论受到了人们的怀疑与攻击,这就是数学史上所说的无穷小悖论。英国哲学家贝克莱对微积分的攻击最为激烈,他说微积分的推导是"分明的诡辩"。
直到19世纪,柯西和魏尔斯特拉斯等人引入了ε-δ语言,才真正建立起分析学的严密基础。柯西把无穷小视为"以0为极限的变量",这正确地确立了"无穷小"概念为"似零不是零却可以人为用等于0处理"的办法。
二、六种自变量变化趋势的严格定义
下面通过表格概括六种自变量变化趋势及其极限定义:
| 自变量趋势类型 | 数学符号表示 | 极限定义核心思想 |
|---|---|---|
| x 趋向 x0x_0x0 | x→x0x→x_0x→x0 | x无限接近x0x_0x0,但永远不等于 x0x_0x0 的过程 |
| x 从左侧趋向 x0x_0x0 | x→x0−x \to x_0^-x→x0− | x无限接近x0x_0x0,但永远小于 x0x_0x0 的过程 |
| x 从右侧趋向 x0x_0x0 | x→x0+x \to x_0^+x→x0+ | x无限接近x0x_0x0,但永远大于 x0x_0x0 的过程 |
| x 趋向正无穷大 | x→+∞x \to +\inftyx→+∞ | x无限增大的过程,x的值可以大于任意指定的数 |
| x 趋向负无穷大 | x→−∞x \to -\inftyx→−∞ | x无限减小的过程,x的值可以小于任意指定的数 |
| x 趋向无穷大 | x→∞x \to \inftyx→∞ | x的绝对值|x|无限增大的过程,|x|的值可以大于任意指定的数 |
2.1 邻域与去心邻域的概念
定义: 设 x0∈R,ε>0x_0 \in R,\varepsilon > 0x0∈R,ε>0,则称集合 {x∣∣x−x0∣<ε}\{x \mid |x-x_0| < \varepsilon \}{x∣∣x−x0∣<ε} 为 x0x_0x0 的邻域,记作 U(x0,ε)U(x_0,\varepsilon)U(x0,ε),即 U(x0,ε)=(x0−ε,x0+ε)U(x_0,\varepsilon) = (x_0-\varepsilon, x_0 + \varepsilon)U(x0,ε)=(x0−ε,x0+ε)。
集合 {x∣0<∣x−x0∣<ε}\{x \mid 0 < |x-x_0| < \varepsilon \}{x∣0<∣x−x0∣<ε} 称为 x0x_0x0 的去心邻域,记作 U0(x0,ε)U^0(x_0,\varepsilon)U0(x0,ε),即 U0(x0,ε)=(x0−ε,x0)∪(x0,x0+ε)U^0(x_0,\varepsilon) = (x_0-\varepsilon,x_0) \cup (x_0,x_0 + \varepsilon)U0(x0,ε)=(x0−ε,x0)∪(x0,x0+ε)。
邻域的概念是理解极限的基础,它描述了点x0x_0x0附近的区域,而去心邻域则排除了点x0x_0x0本身,这与极限考虑的是"接近但不等于"的思想一致。
三、函数在一点的极限与单侧极限
3.1 函数在 x → x 0 x \to x_0 x→x0时的极限
定义: 设函数f(x)f(x)f(x)在x0x_0x0的某去心邻域内有定义。若对于任意给定的正数ε\varepsilonε,总存在正数δ\deltaδ,使得当0<∣x−x0∣<δ0 < |x-x_0| < \delta0<∣x−x0∣<δ时,有∣f(x)−A∣<ε|f(x)-A| < \varepsilon∣f(x)−A∣<ε成立,则称函数f(x)f(x)f(x)在xxx趋向x0x_0x0时有极限,称AAA为函数f(x)f(x)f(x)趋向x0x_0x0时的极限,记作:
limx→x0f(x)=A\lim_{x \to x_0} f(x) = Ax→x0limf(x)=A
这一定义由柯西首先提出,后由魏尔斯特拉斯完善,称为极限的ε-δ定义。该定义的核心是:无论要求函数值多么接近极限值A(由ε控制),只要自变量x足够接近x0x_0x0(由δ控制),这个接近程度就能得到保证。
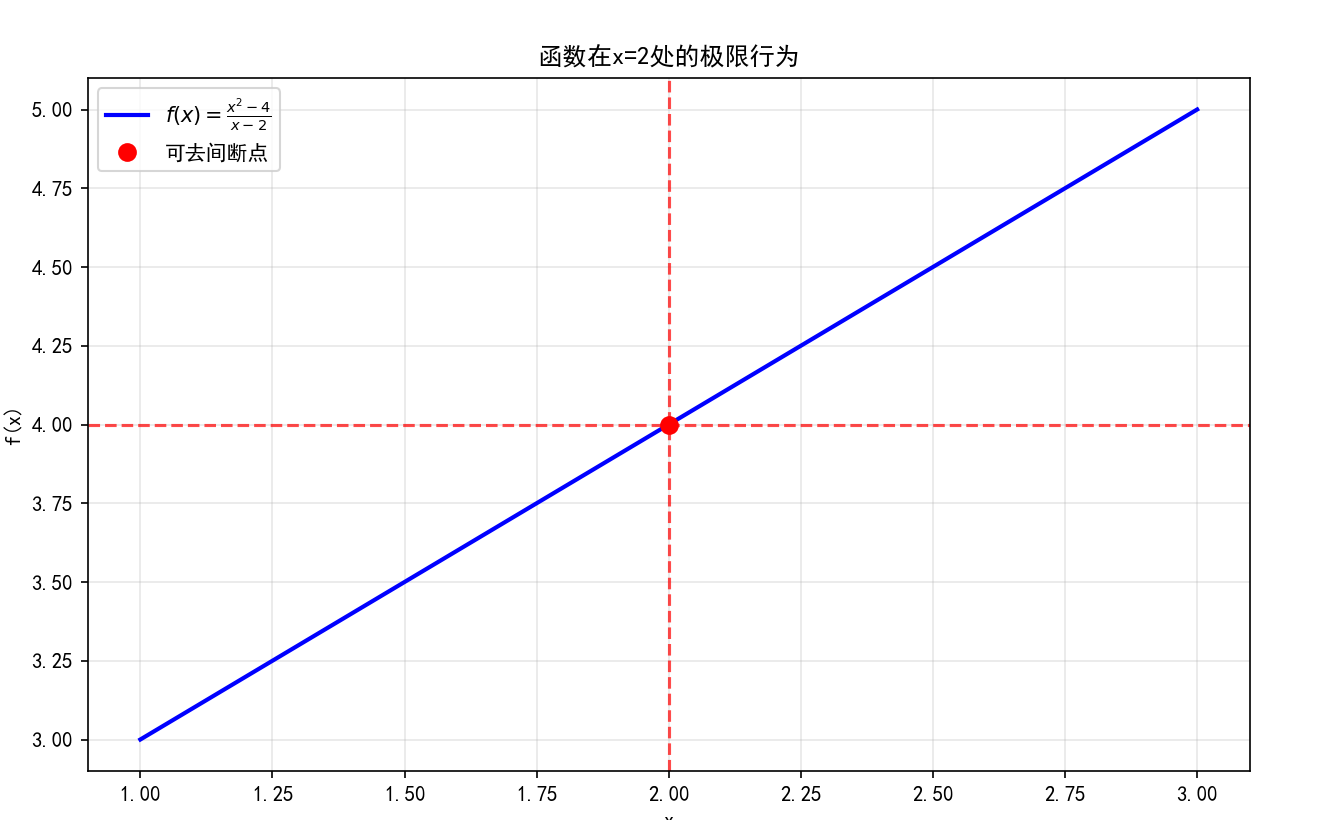
考虑函数f(x)=x2−4x−2f(x) = \frac{x^2-4}{x-2}f(x)=x−2x2−4在x→2x \to 2x→2时的极限。虽然在x=2处函数无定义(分母为零),但通过因式分解可简化函数为f(x)=x+2f(x)=x+2f(x)=x+2(当x≠2x \neq 2x=2),因此极限值为4。
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False# 分析 f(x) = (x^2-4)/(x-2) 在 x->2 的极限
x = sp.symbols('x')
f = (x**2 - 4)/(x - 2)# 简化函数(x ≠ 2时等价)
f_simplified = sp.simplify(f)
print(f"简化后的函数: {f_simplified}")# 计算极限
limit_value = sp.limit(f, x, 2)
print(f"x->2时函数的极限: {limit_value}")# 可视化
x_vals = np.linspace(1, 3, 400)
x_vals = x_vals[x_vals != 2] # 排除x=2
y_vals = (x_vals**2 - 4) / (x_vals - 2)plt.figure(figsize=(10, 6))
plt.plot(x_vals, y_vals, 'b-', linewidth=2, label=r'$f(x) = \frac{x^2-4}{x-2}$')
plt.plot(2, 4, 'ro', markersize=8, label='可去间断点')
plt.axhline(y=4, color='r', linestyle='--', alpha=0.7)
plt.axvline(x=2, color='r', linestyle='--', alpha=0.7)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('函数在x=2处的极限行为')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
运行结果:
3.2 单侧极限及其重要性
单侧极限考虑自变量从特定方向接近x0x_0x0时函数的行为,分为左极限(x→x0−)(x→x_0^-)(x→x0−)和右极限(x→x0+)(x→x_0^+)(x→x0+)。
数学表示:
- 左极限:limx→x0−f(x)\lim \limits_{x \to x_0^-} f(x)x→x0−limf(x)
- 右极限:limx→x0+f(x)\lim \limits_{x \to x_0^+} f(x)x→x0+limf(x)
定理: 函数在一点极限存在的充要条件是左右极限存在且相等。即: limx→x0f(x)=A⟺limx→x0−f(x)=limx→x0+f(x)=A\lim_{x \to x_0} f(x) = A \iff \lim_{x \to x_0^-} f(x) = \lim_{x \to x_0^+} f(x) = Ax→x0limf(x)=A⟺x→x0−limf(x)=x→x0+limf(x)=A
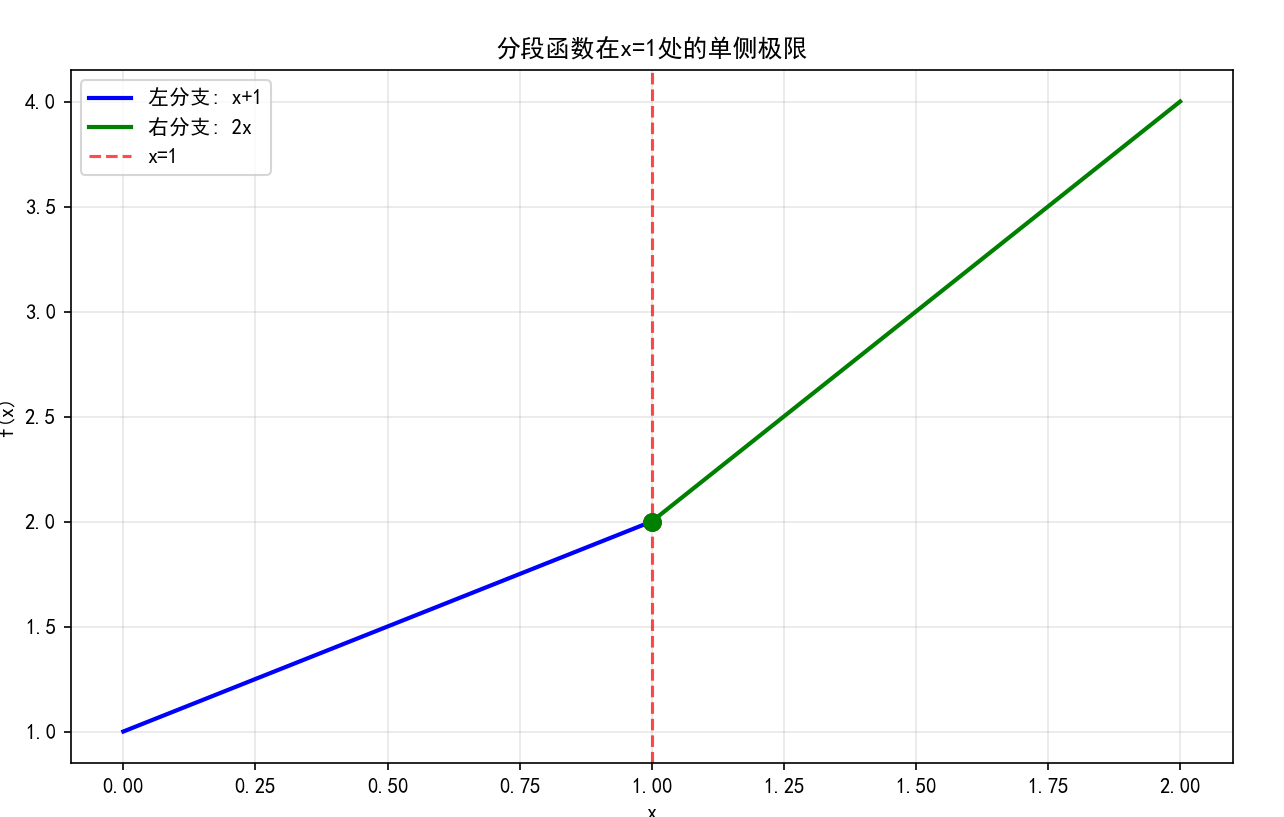
分析分段函数f(x)={x+1,x<12x,x≥1f(x) = \begin{cases} x+1, & x < 1 \\ 2x, & x \geq 1 \end{cases}f(x)={x+1,2x,x<1x≥1在x→1x \to 1x→1处的极限行为:
import numpy as np
import matplotlib.pyplot as plt
import sympy as sp# 定义符号变量
x = sp.Symbol('x')# 分析分段函数在x->1处的单侧极限
def piecewise_function(x_val):if x_val < 1:return x_val + 1else:return 2 * x_val# 计算左右极限
left_limit = sp.limit(x + 1, x, 1, dir='-')
right_limit = sp.limit(2*x, x, 1, dir='+')print(f"左极限: {left_limit}")
print(f"右极限: {right_limit}")
print(f"函数在x=1处的极限存在: {left_limit == right_limit}")# 可视化
x_vals_left = np.linspace(0, 0.999, 100)
x_vals_right = np.linspace(1.001, 2, 100)
y_vals_left = [piecewise_function(x) for x in x_vals_left]
y_vals_right = [piecewise_function(x) for x in x_vals_right]plt.figure(figsize=(10, 6))
plt.plot(x_vals_left, y_vals_left, 'b-', linewidth=2, label='左分支: x+1')
plt.plot(x_vals_right, y_vals_right, 'g-', linewidth=2, label='右分支: 2x')
plt.axvline(x=1, color='r', linestyle='--', alpha=0.7, label='x=1')
plt.plot(1, 2, 'ro', markersize=8)
plt.plot(1, 2, 'go', markersize=8)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('分段函数在x=1处的单侧极限')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
执行结果:

四、函数在无穷远处的极限
4.1 无穷远极限的定义
设函数f(x)f(x)f(x)在∣x∣|x|∣x∣充分大时有定义,AAA是一个常数。若对于任意的正数ε\varepsilonε,总存在正数XXX,使得对于满足∣x∣>X|x| > X∣x∣>X的所有xxx,都有∣f(x)−A∣<ε|f(x) - A| < \varepsilon∣f(x)−A∣<ε成立,则函数f(x)f(x)f(x)在x→∞x \to \inftyx→∞时的极限是AAA,记作:
limx→∞f(x)=A\lim_{x \to \infty} f(x) = Ax→∞limf(x)=A
类似地,可以定义x→+∞x \to +\inftyx→+∞和x→−∞x \to -\inftyx→−∞时的极限。
定理: 极限limx→∞f(x)=A\lim \limits_{x \to \infty} f(x) = Ax→∞limf(x)=A存在的充分必要条件是:极限limx→+∞f(x)=A\lim \limits_{x \to +\infty} f(x) = Ax→+∞limf(x)=A与极限limx→−∞f(x)=A\lim \limits_{x \to -\infty} f(x) = Ax→−∞limf(x)=A均存在且相等。
4.2 无穷远极限的示例
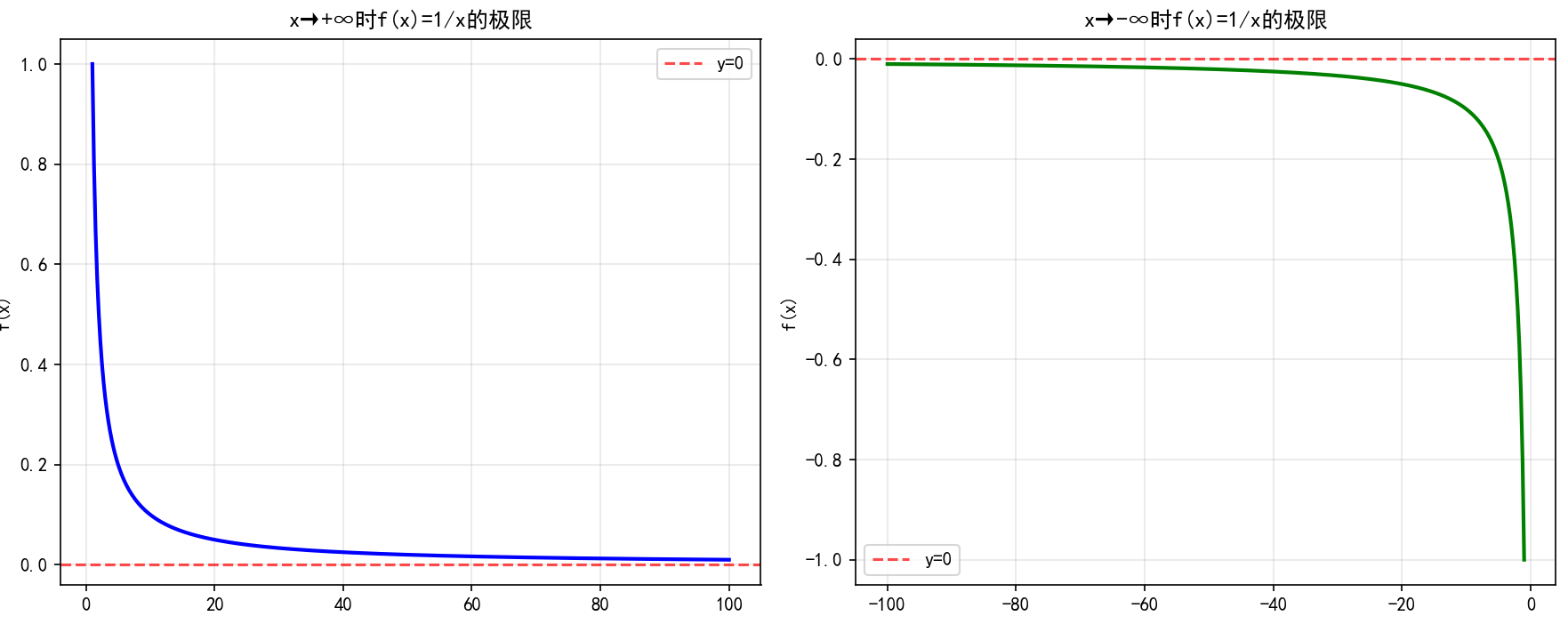
以函数f(x)=1xf(x)=\frac{1}{x}f(x)=x1为例,分析其在无穷远处的行为:
import numpy as np;
import matplotlib.pyplot as plt;
import sympy as sp;x = sp.Symbol('x')# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False# 分析函数在无穷远处的极限
def f(x):return 1/x# 计算极限
limit_plus_inf = sp.limit(1/x, x, sp.oo)
limit_minus_inf = sp.limit(1/x, x, -sp.oo)print(f"x->+∞时函数的极限: {limit_plus_inf}")
print(f"x->-∞时函数的极限: {limit_minus_inf}")# 可视化
x_vals_positive = np.linspace(1, 100, 400)
x_vals_negative = np.linspace(-100, -1, 400)
y_vals_positive = f(x_vals_positive)
y_vals_negative = f(x_vals_negative)plt.figure(figsize=(12, 5))plt.subplot(1, 2, 1)
plt.plot(x_vals_positive, y_vals_positive, 'b-', linewidth=2)
plt.axhline(y=0, color='r', linestyle='--', alpha=0.7, label='y=0')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('x→+∞时f(x)=1/x的极限')
plt.legend()
plt.grid(True, alpha=0.3)plt.subplot(1, 2, 2)
plt.plot(x_vals_negative, y_vals_negative, 'g-', linewidth=2)
plt.axhline(y=0, color='r', linestyle='--', alpha=0.7, label='y=0')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('x→-∞时f(x)=1/x的极限')
plt.legend()
plt.grid(True, alpha=0.3)plt.tight_layout()
plt.show()
运行结果:

五、数列的极限
5.1 数列极限的定义
数列可视为定义域为正整数的特殊函数,数列极限研究当项数nnn无限增大时数列项ana_nan的变化趋势。
定义: 对于数列{an}\{a_n\}{an},如果存在常数LLL,对于任意给定的ε>0\varepsilon > 0ε>0,总存在正整数NNN,使得当n>Nn > Nn>N时,有∣an−L∣<ε|a_n - L| < \varepsilon∣an−L∣<ε恒成立,则称数列{an}\{a_n\}{an}收敛于LLL,记作:
limn→∞an=L\lim_{n \to \infty} a_n = Ln→∞liman=L
这一定义称为数列极限的ε-N定义,是魏尔斯特拉斯在柯西基础上完善的严格定义。
当数列{an}\{a_n\}{an}存在极限时,则称{an}\{a_n\}{an} 收敛;当数列 {an}\{a_n\}{an} 不存在极限时,则称 {an}\{a_n\}{an} 发散。
对于数列 {an}\{a_n\}{an} ,自变量只有一个变化趋势 n→+∞n \to +\inftyn→+∞ , 而且 n 不能取负数,这时 n→+∞n \to +\inftyn→+∞ 也简记为 n→∞n \to \inftyn→∞。
5.2 数列极限的示例与分析
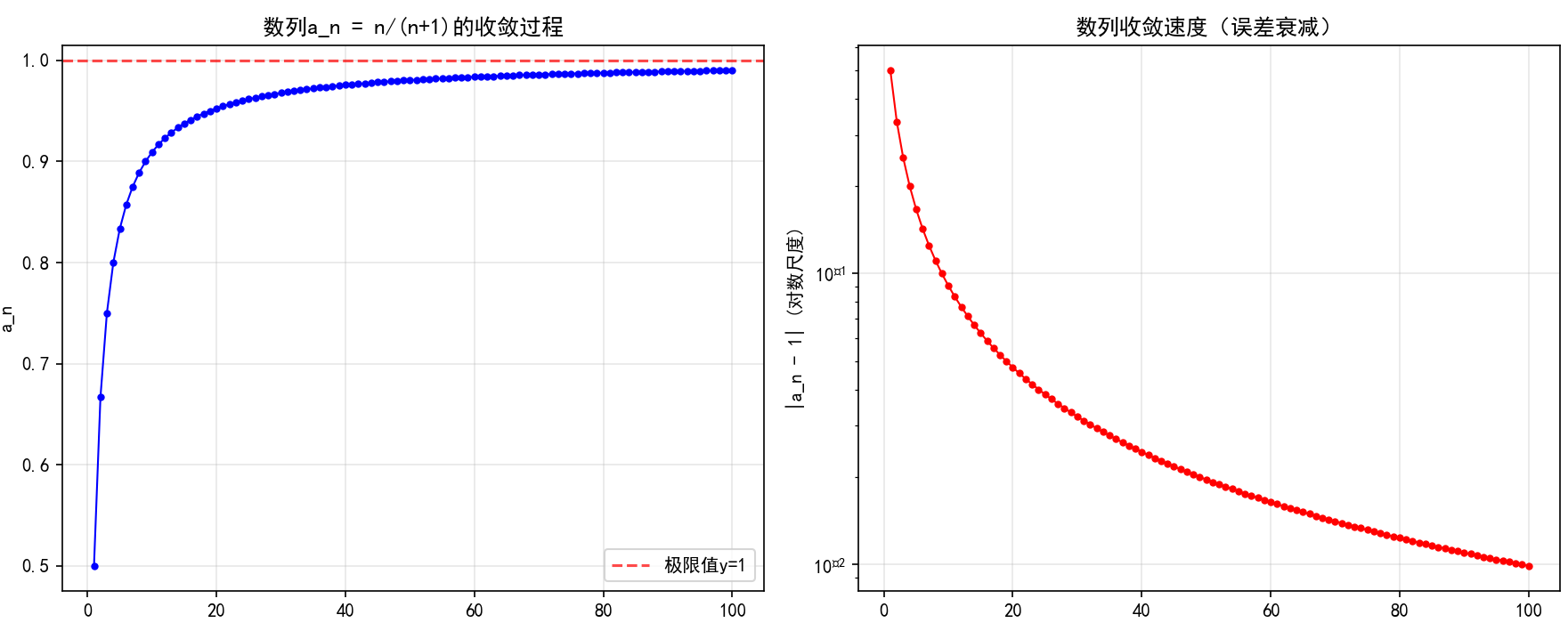
考虑数列an=nn+1a_n = \frac{n}{n+1}an=n+1n,分析其收敛性:
# 分析数列极限
n = sp.symbols('n', integer=True)
a_n = n/(n+1)# 计算数列极限
sequence_limit = sp.limit(a_n, n, sp.oo)
print(f"数列a_n = n/(n+1)的极限: {sequence_limit}")# 可视化数列收敛过程
n_vals = np.arange(1, 101)
a_n_vals = n_vals / (n_vals + 1)plt.figure(figsize=(12, 5))plt.subplot(1, 2, 1)
plt.plot(n_vals, a_n_vals, 'bo-', markersize=3, linewidth=1)
plt.axhline(y=1, color='r', linestyle='--', alpha=0.7, label='极限值y=1')
plt.xlabel('n')
plt.ylabel('a_n')
plt.title('数列a_n = n/(n+1)的收敛过程')
plt.legend()
plt.grid(True, alpha=0.3)# 展示收敛速度(误差随n增大而减小)
errors = np.abs(a_n_vals - 1)
plt.subplot(1, 2, 2)
plt.semilogy(n_vals, errors, 'ro-', markersize=3, linewidth=1)
plt.xlabel('n')
plt.ylabel('|a_n - 1| (对数尺度)')
plt.title('数列收敛速度(误差衰减)')
plt.grid(True, alpha=0.3)plt.tight_layout()
plt.show()
运行结果:
六、极限的理论意义与应用
6.1 极限在微积分中的核心地位
极限概念是现代数学分析的基础,几乎所有高等数学概念都建立在极限之上:
- 函数连续性:函数在一点连续的定义是当自变量的增量趋于零时,函数值的增量趋于零的极限。
- 导数:函数在某点的导数定义为函数值的增量与自变量的增量之比当自变量增量趋于零时的极限。
- 积分:定积分定义为当分割的细度趋于零时,积分和式的极限。
- 级数敛散性:数项级数的敛散性是用部分和数列的极限来定义的。
6.2 极限思想的哲学意义
极限概念体现了有限与无限的对立统一关系:
- 序列x1,x2,...,xn,...x_1, x_2, ..., x_n, ...x1,x2,...,xn,...是由无限多个有限值组成的,并且在收敛的条件下,存在着有限的极限值。
- 这说明了无限包含着有限,并且在一定条件下,可以向有限转化。
- 另一方面,有限又包含着无限,在一定条件下,可以转化为无限,并通过无限表现自身。
这种有限与无限的辩证关系是微积分能够解决实际问题的哲学基础。
总结
极限概念从六个不同角度描述了函数和数列的变化趋势,构成了微积分学的理论基础。通过ε-δ和ε-N语言,极限概念获得了严格的数学表述,使微积分从依赖直观的经验科学转变为逻辑严谨的数学分支。
掌握六种自变量变化趋势下的极限定义,是理解导数、积分、无穷级数等高等数学内容的必经之路。极限思想不仅具有数学意义,更体现了人类思维从有限认识无限、从近似认识精确的能力。
进一步学习建议:深入理解ε-δ定义,掌握极限的严格证明方法,并探索极限在微分方程、数值分析等领域的应用。
