链式结构二叉树：结点定义、创建及全操作实现（遍历 / 计数 / 销毁 / 判断完全二叉树）

实现链式结构二叉树

链式结构二叉树：底层实现链表进行实现，链表中的每一个结点由三个域组成，分别为数据域和左右指针域，左右指针分别用来存储该节点左右孩子的地址。

结点结构如下：

typedef int BTDataType;
//创造树的结构
typedef struct BinaryTreeNode
{BTDataType val;//存储结点数据struct BinaryTreeNode* left;//指向当前结点的左孩子struct BinaryTreeNode* right;//指向当前结点的右孩子
}BTNode;

1 二叉树的简单创建

BTNode* BuyBTNode(BTDataType val)
{//创造空间节点BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc failed");exit(1);}newnode->val = val;newnode->left = newnode->right = NULL;return newnode;
}
BTNode* CreateTree()
{BTNode* n1 = BuyBTNode(1);BTNode* n2 = BuyBTNode(2);BTNode* n3= BuyBTNode(4);BTNode* n4 = BuyBTNode(3);BTNode* n5 = BuyBTNode(5);BTNode* n6 = BuyBTNode(6);n1->left = n2;n1->right = n3;n2->left = n4;n3->left = n5;n3->right = n6;return n1;
}

构建一个BuyBTNode函数创造二叉树的结点，并用CreateTree函数通过赋值各结点左右指针构成一个简单的二叉树。

最终二叉树的结构图示：

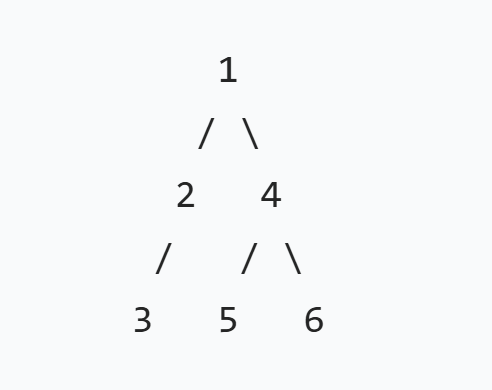
由于链式结构二叉树的底层是链表，所以不像数组那样结点空间是连续的可以得到一个头的位置就可以遍历整个数组，我们二叉树的每一个结点只有左右两个指针，所以我们只能通过一个结点找到它的左右孩子结点。但其实我们仔细观察二叉树的结构就知道二叉树类似一个套娃（递归结构），根节点的左右子树分别又是由子树结点、子树结点的左子树、子树结点的右子树组成的。所以二叉树本质就是一个递归结构，所以我们对二叉树的各项操作也是通过递归实现的。

下面功能函数的实现基本都是递归！！！

2 二叉树的遍历

二叉树的遍历由三种类型：

• 前序遍历（PreorderTraversal）：访问根结点的操作发⽣在遍历其左右⼦树之前
  访问顺序为：根结点、左⼦树、右子树。
• 中序遍历(InorderTraversal)：访问根结点的操作发⽣在遍历其左右⼦树之中
  访问顺序为：左⼦树、根结点、右⼦树
• 后序遍历(PostorderTraversal)：访问根结点的操作发⽣在遍历其左右⼦树之后
  访问顺序：左⼦树、右⼦树、根结点
  这些遍历类型本质就是根据根结点的位置来确定的。

2.1 前序遍历

void PreOrder(BTNode* root)
{if (root == NULL){return;}printf("%c ", root->val);PreOrder(root->left);PreOrder(root->right);
}

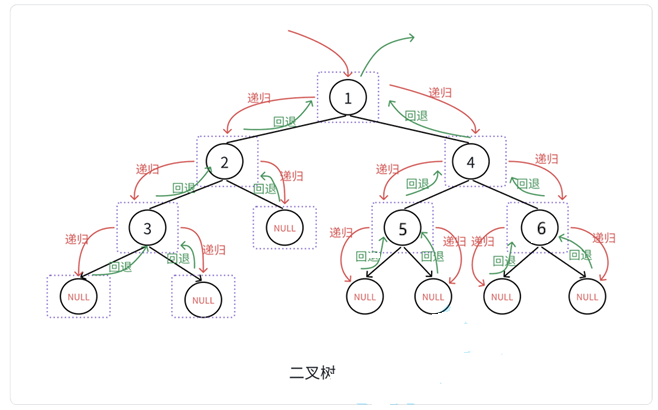
前序遍历图：

函数递归栈图：

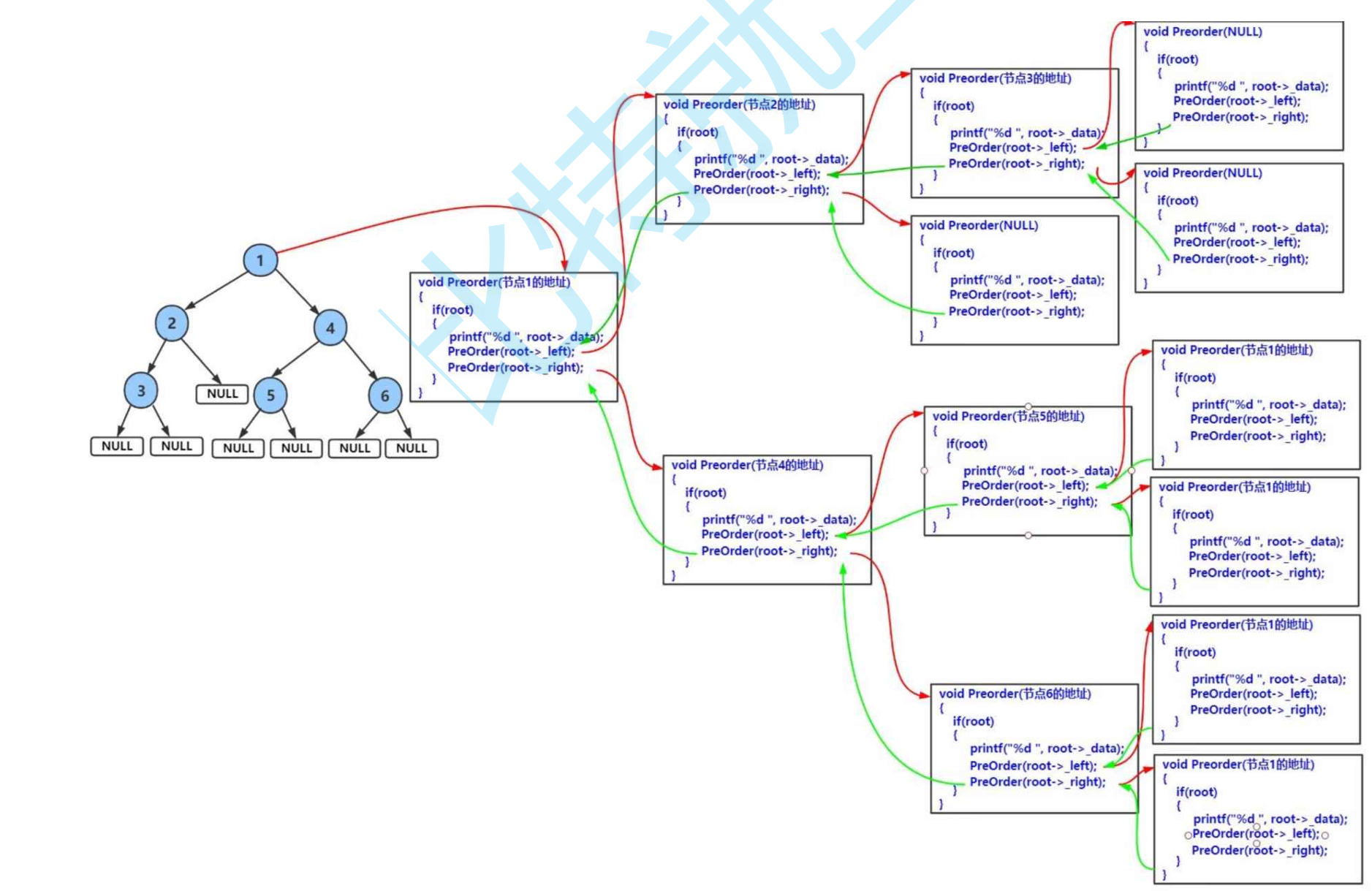
递归的终止条件为root==NULL，printf("%c ", root->val)打印出这个头节点，再用PreOrder(root->left)和PreOrder(root->right)将这个递归问题分解为以左右子树为根结点的更小的问题。

2.2 中序遍历

void InOrder(BTNode* root)
{if (root==NULL){return;}InOrder(root->left);printf("%d ", root->val);InOrder(root->right);
}

我们先打印左节点，再打印根结点，最后打印右节点。所以我们将printf("%d ", root->val)放在InOrder(root->left)和InOrder(root->right)的之间。

2.3 后序遍历

void PostOrder(BTNode* root)
{if (root ==NULL){return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->val);
}

由于最后打印根结点，所以将根结点放在最后面。

递归写遍历的小结：我们一开始不要将目光聚焦在全部繁琐的遍历结构之中，我们只要知道最简单的当前根结点，左孩子和右孩子就行了。

2.4 二叉树结点个数

int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}return 1+BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}

二叉树结点个数=根结点+左子树结点个数+右子树结点个数。

2.5 二叉树叶子结点个数

int BinaryTreeLeafSize(BTNode* root)
{if (root->left||root->right){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

二叉树叶子结点个数=左子树叶子结点个数+右子树叶子结点个数。叶子结点的特征就是左节点或者右结点为NULL。

2.6 二叉树第K层结点个数

int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->left, k-1) + BinaryTreeLevelKSize(root->right, k-1);
}

首先我们要明确我们遍历到二叉树的哪里时是第K层，随着二叉树往下的遍历直到k==1时此时如果结点非NULL，则这个结点就是一个K层的结点。

2.7 二叉树的深度

int BinaryTreeDepth(BTNode* root)
{if (root == NULL){return 0;}int left_depth = BinaryTreeDepth(root->left);int right_depth = BinaryTreeDepth(root->right);return 1 + (left_depth > right_depth ? left_depth : right_depth);
}

二叉树的的深度=最深的子树+1。

2.8 二叉树查找值为x的结点

BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}if (root->val == x){return root;}BTNode* left_pr = BinaryTreeFind(root->left,x);if (left_pr){return left_pr;}BTNode* right_pr = BinaryTreeFind(root->right,x);if (right_pr){return right_pr;}return NULL;
}

我们先对根结点判断再对左右子树进行递归查找值为x的结点。

2.9 二叉树销毁

void BinaryTreeDestory(BTNode** root)
{if (*root == NULL){return;}BinaryTreeDestory(&((*root)->left));BinaryTreeDestory(&((*root)->right));(*root)->val = 0;(*root)->left = (*root)->right = NULL;free(*root);*root = NULL;
}

对结点的销毁，我们不能从根结点开始删这样我们会找不到左右结点，同时对于形参要改变实参我们要取实参的地址所以是一个二级指针。

第一部分：
销毁左右结点

BinaryTreeDestory(&((*root)->left));
BinaryTreeDestory(&((*root)->right));

第二部分：
最后销毁头节点

(*root)->val = 0;
(*root)->left = (*root)->right = NULL;
free(*root);
*root = NULL;

2.10 二叉树的层序遍历

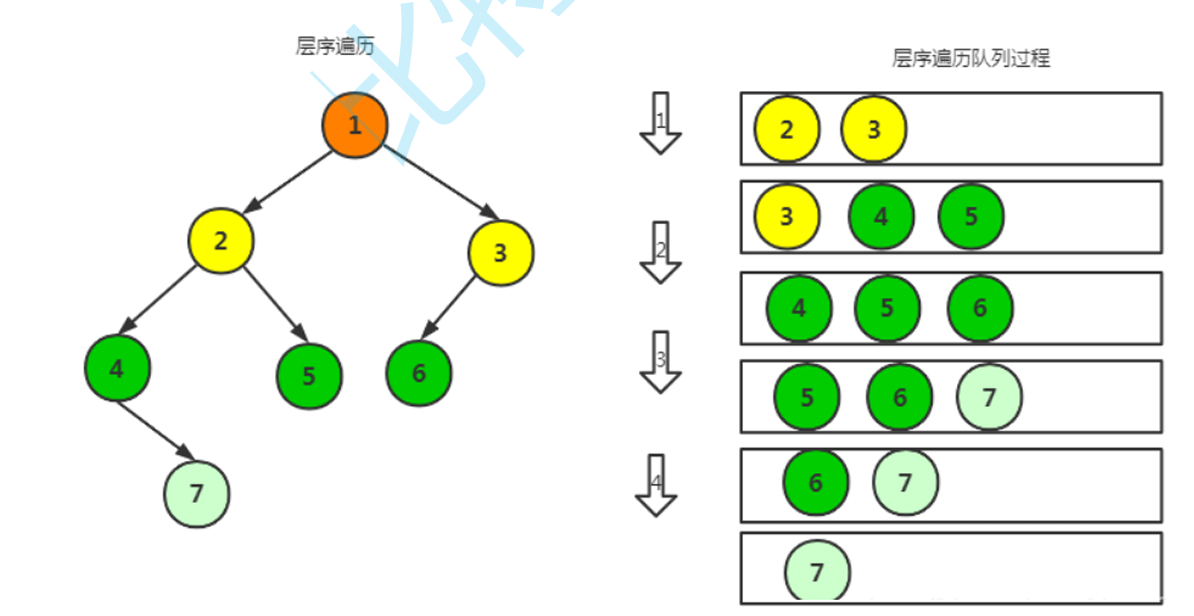
层序遍历就是沿着二叉树的层数从上到小从左到右依次遍历，我们实现这个结构需要队列这个数据结构

void LevelOrder(BTNode* root)
{assert(root);Queue q;QueueInit(&q);QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* temp = QueueFront(&q);printf("%d ", temp->val);if (temp->left){QueuePush(&q, temp->left);}if (temp->right){QueuePush(&q, temp->right);}QueuePop(&q);}
}

第一部分：
我们先创造一个队列并将根结点插入到队列中

Queue q;
QueueInit(&q);
QueuePush(&q, root);

第二部分：
当队列不为空便一直循环，出队列时如果该结点的左右结点存在便将左右结点插入队列之中，从而在队列中排成层序遍历所需要的顺序。

while (!QueueEmpty(&q)){BTNode* temp = QueueFront(&q);printf("%d ", temp->val);if (temp->left){QueuePush(&q, temp->left);}if (temp->right){QueuePush(&q, temp->right);}QueuePop(&q);}

2.11 判断二叉树是否为完全二叉树

bool BinaryTreeComplete(BTNode* root)
{assert(root);Queue q;QueueInit(&q);QueuePush(&q, root);//第一层循环在找到第一个NULL时终止while (!QueueEmpty(&q)){BTNode* temp = QueueFront(&q);QueuePop(&q);if (temp == NULL){break;}//前面这句话也同样使得temp不为NULLQueuePush(&q,temp->left);QueuePush(&q,temp->right);}while (!QueueEmpty(&q)){BTNode* temp = QueueFront(&q);QueuePop(&q);if (temp != NULL){return false;}}return true;
}

完全二叉树与非完全二叉树的区别：完全二叉树在层序遍历的时候中间不会有NULL。而非完全二叉树存在NULL。
完全二叉树图：

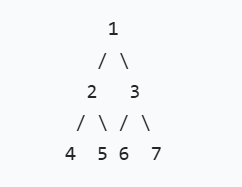
层序遍历中间没有NULL，除非是末尾。

非完全二叉树图：

4和6结点之间就有NULL。

判断二叉树是否为完全二叉树详细刨析
第一部分：
由于要层序遍历判断所以先建立一个队列

Queue q;
QueueInit(&q);
QueuePush(&q, root);

第二部分：
当层序遍历循环碰到结点为NULL时就停止

if (temp == NULL){break;}//前面这句话也同样使得temp不为NULLQueuePush(&q,temp->left);QueuePush(&q,temp->right);}

特别说明：由于判断是否是完全二叉树要靠判断中间是不是有NULL结点，所以与层序遍历不同，结点的左右孩子为根结点也要添加入队列之中。
第三部分：
继续层序判断这个NULL是中间的还是末尾位置的，如果后面层序遍历还有不为NULL的结点出现，则这个NULL处在中间位置就不是完全二叉树。否则遍历完后就是完全二叉树。

while (!QueueEmpty(&q)){BTNode* temp = QueueFront(&q);QueuePop(&q);if (temp != NULL){return false;}}return true;